融合支持度和不确定度的D-S证据理论及应用

任会娟，黄丽霞，张雪英，李凤莲，杜海文，于丽君

(1.太原理工大学 信息与计算机学院，太原 030024；2.山西省中电科新能源技术有限公司，太原 030024)

由于生产环境、生产次数，测量误差等诸多因素，沉积数据往往具有显著的不确定性。D-S证据理论作为一种处理不确定性问题的理论方法，及其在不确定信息的表示、处理和组合等方面的优势，已经广泛使用于决策融合的不确定性推理系统中[1]。但是D-S证据理论在处理冲突证据时，容易产生与事实相悖的结果，不利于实际生产应用。

针对上述问题，现有研究方向主要包括：改变Dempster组合规则[2-3]和修正原证据体[4-5]。前者认为组合规则本身存在缺陷需要修改，但修改破坏了D-S证据理论的完整性[6]，在处理大量证据时，效果并不理想；后者认为悖论的出现主要是由于证据本身的缺陷导致，即存在一个或多个冲突证据，而解决冲突问题关键是通过折扣系数对证据进行修正，减小冲突证据的占比，削减证据的冲突程度，最大程度上保留了D-S证据理论的完整性。因此，本文将折扣系数的确定方式作为研究的重点。

目前，折扣系数的确定方法分两种：一种是利用距离衡量证据的不确定性；另一种是基于相关系数描述冲突程度[7-8]。前者又可分为两类：一类是点到点距离。文献[9]通过分析Jousselme距离提出广义证据距离，但是很难用一个点衡量不确定区间，不可避免地造成信息的丢失；另一类是区间距离[10-11]。文献[12]利用基于定积分的区间距离衡量证据的不确定性并得到很好的融合效果。关于后者，文献[13]使用Pearson相关系数对证据进行修正，但Pearson相关系数适用于符合正态分布的数据，对数据源的要求很高。文献[14]使用Spearman相关系数有效的解决了这一问题，但没有考虑到证据的不确定性，造成了部分信息的丢失。

综上所述，本文在相关性和置信区间的基础上，引入Spearman相关系数和基于定积分的区间距离来分别描述和计算证据间的支持度以及各证据的不确定度，并根据这两个指标，确定新的折扣系数以修正原证据体。以此为基础，建立一种基于改进D-S证据理论的碳/碳复合材料沉积质量预测模型，为碳/碳复合材料的沉积过程提供有效参考。

碳/碳复合材料，是一种具有较好物理性能和力学性能的新型复合材料，广泛应用于航空航天、导航、核能等高科技领域[15]。但是目前国内外绝大多数的研究主要针对致密技术进行实验和研究[16-17]，而随着生产数据的增多和实际生产的需要，对致密化过程产生的数据进行智能分析，发现各工序之间的关系及最后的作用效果，对于开展碳/碳复合材料沉积质量预测的研究具有重要意义。

1 D-S证据理论

下面给出D-S证据理论相关定义：

定义1 设Θ为识别框架，基本信任分配函数m是一个从集合2Θ到[0,1]的映射，A表示识别框架Θ的任一子集，记为A⊆Θ，且满足[8]：

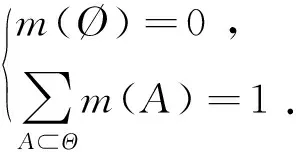
(1)

式中：m(A)称为命题A的基本概率分配(Basic Probability Assignment，BPA)函数，表示证据对的信任程度。

定义2 假设Θ为识别框架，m为BPA函数，则

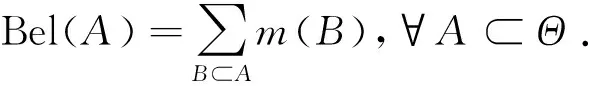
(2)

Bel(A)为信任函数，表示命题A所有子集的BPA之和。

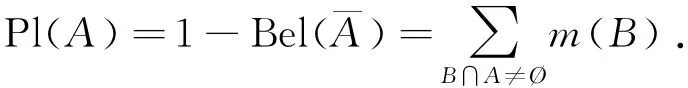
(3)

Pl(A)为似然函数，表示命题A非假的信任程度。[Bel(A),Pl(A)]为置信区间或不确定区间，区间的长度反映了命题A的不确定程度[15]。

定义3 设m1,m2,…,mn是同一识别框架Θ上的n个BPA函数，焦元分别为Ai(i=1,2,…,N)，则D-S证据理论的合成规则为：

(4)

2 改进的D-S证据理论

本节针对Spearman相关系数的规范性问题进行说明并加以改进，并对支持度和不确定度对于冲突度量的必要性进行分析；最后，提出融合支持度和不确定度的D-S证据理论，并详细介绍所提理论对于冲突证据融合流程。

2.1 Spearman相关系数的规范性问题及改进方法

虽然Spearman相关系数在非正态分布的样本上表现优异，但将其引入到D-S证据理论进行证据修正时，仍存在以下问题：

1) 忽略了相关系数为[-1,0)和0时的区别；

2) 默认样本值无重复。

下面将给出原始的Spearman相关系数定义，如定义3，并对以上两个问题分别展开讨论并举例说明：

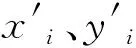
(5)

为变量x和y之间的Spearman相关系数。其中，di为变量x和y之间的等级差。r取值范围为[-1,1]，r的值越大，x、y相似性越高。当r=1时，x和y在函数上严格单调递增。当r=-1时，x和y在函数上严格单调递减。当r=0时，x和y的单调关系在函数上并不明显[17]。

针对Spearman相关系数取值无法满足基本概率分配函数要求的情况，即m(A)>0且∑A⊂Θm(A)=1.文献[17]将Spearman相关系数为[-1,0]的全部归零，即r=0；认为r为负数的证据完全冲突，忽略了r为负数的证据的冲突程度也有区分，以下进行举例说明。

例1：设辨识框架Θ={A,B,C}，3个证据的基本概率分配如下：

m1∶m1(A)=0.8,m1(B)=0.2,m1(C)=0；

m2∶m2(A)=0,m2(B)=0.8,m2(C)=0.2；

m3∶m3(A)=0.3,m3(B)=0.5,m3(C)=0.2.

推理m1对命题A的信度较高，且m1和m2对命题B的均有信度，即具有一定的相关性；较m2，m3对命题A的信度有所上升，且对命题B的信度有所下降，m1和m3的相关性应大于m1和m2的相关性。

根据文献[17]的计算方式得，m1和m2之间的Spearman相关系数r12=0，m1和m3的r13=0，与上述推理结果不符。

针对这一问题，对Spearman相关系数计算公式(5)进行改进，由于原始Spearman相关系数的取值范围为[-1,1]，对其进行加1处理，使其取值范围变[0,2]；再次对整体除以2，为使之取值范围变为[0,1]，改进后的Spearman相关系数计算公式，如式(6)所示：

(6)

其中，n为焦元个数，di为焦元之间的等级差。改进之后的Spearman相关系数既考虑了相关系数为[-1,0)和0时的区别，又满足了基本概率分配函数的要求。

根据公式(6)计算得，m1和m2的r12=0.25，m1和m3的r13=0.75，与上述推理结果完全吻合。

另外，针对Spearman相关系数默认样本值要求无重复的缺陷，考虑证据的BPA无法保证无重复。因此，在计算时，对存在重复值的部分取等级均值。以下进行举例说明：

例2：设辨识框架Θ={A,B,C}，两个证据的基本概率分配如下：

m1∶m1(A)=0.5,m1(B)=0.2,m1(C)=0.3；

m2∶m2(A)=0.6,m2(B)=0.2,m2(C)=0.2.

若不对等级取均值，由公式(6)计算可得，m1和m2的r12=0.75.对重复值的部分取等级均值得m1的等级分别为1，3，2；m2的等级分别为1，2.5，2.5.则m1和m2的r12=0.937 5.对存在重复值的部分取等级均值，m1和m2之间的支持度相对较高。

2.2 支持度和不确定度的必要性分析

支持度是从证据间的相互性出发，描述证据间的变化趋势是否相关，而证据的不确定度是以证据本身特性作为依据，用来反映证据的聚集程度，不确定度越高，说明证据的聚集程度越低，对自身的BPA分配越不认可；反之，对自身的BPA分配的认可度越高。所以，证据间的支持度和证据自身的不确定度互不影响，且都属于证据自身所拥有的信息。仅考虑其中之一，都将破坏证据信息的完整性，不利于对冲突证据的有效修正。

因此本文的研究重点是相关系数和区间距离在证据体上的具体应用以及新的折扣系数的确定。

2.3 融合支持度和不确定度的D-S证据理论

由上述研究可知，综合考虑证据间的支持度和证据的不确定度，可以有效描述证据间的信任程度，并且对证据的聚集程度也得以体现，最大程度上利用了证据信息。以此为基础，构建融合支持度和不确定度的D-S证据理论。通过证据间的支持度和证据的不确定度，确定新的折扣系数，修正原证据体，削减证据的冲突程度以达到正确融合的效果。具体的流程如图1所示。

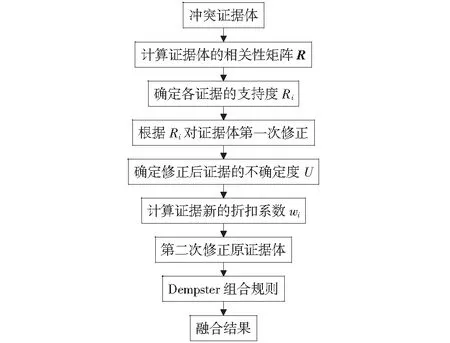
图1 冲突证据融合流程图Fig.1 Conflict evidence fusion flowchart

多证据融合方法和步骤具体如下：

1) 利用式(6)计算两两证据之间的相关系数rij，并构成证据体的相关性矩阵

(7)

其中，n为证据体的证据个数。

2) 根据相关性矩阵，确定证据体对各证据的支持度。定义证据体对证据mi(i=1,2,…,n)的支持度：

(8)

其中，Ri的取值范围为[0,1].

3) 将证据的支持度Ri作为折扣公式：

(9)

中的折扣系数αi，对原证据体进行第一次修正。

4) 在考虑了证据体对各证据支持度的基础上，结合修正后证据体中各证据的置信区间和基于定积分的区间距离：

(10)

确定修正后证据体中各证据自身的不确定度Ui.

公式(10)中，E、F为两个区间，表示为[eu,el]、[fu,fl]，D(E,F)的取值范围为[0,1]，本文对p取1.有关基于定积分区间距离的其他性质，参考文献[15].

各证据自身不确定度Ui的计算步骤如下：

①使用Dempster组合规则对第一次修正后的证据体进行融合，得到结果中BPA最大的焦元A′(A′⊂A)；

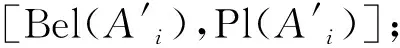
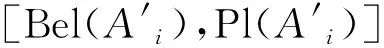
5) 根据各证据的支持度和不确定度计算新的折扣系数：

wi=Ri×(1-Ui) .

(11)

式中，wi的取值范围为[0,1].证据的支持度越大，不确定度越小，则证据的可靠性越强，即折扣系数越大。当证据的支持度Ri=0或Ui=1时，证据的折扣系数wi=0，即该证据与其他证据完全冲突或者该证据对融合结果完全不信任，将从证据体剔除。当证据的支持度Ri=1并且Ui=0时，证据的折扣系数wi=1.

6) 将新的折扣系数带入式(9)，对原证据体进行第二次修正。

7) 使用Dempster组合规则对第二次修正后的证据体进行融合，对应BPA最高的焦元为最终的融合结果。

2.4 算例分析

以文献[18]中提到的4种常见悖论的BPA函数为数据源，如表1所示。从方法的有效性方面，对比几个经典改进算法，对比结果如表2所示。

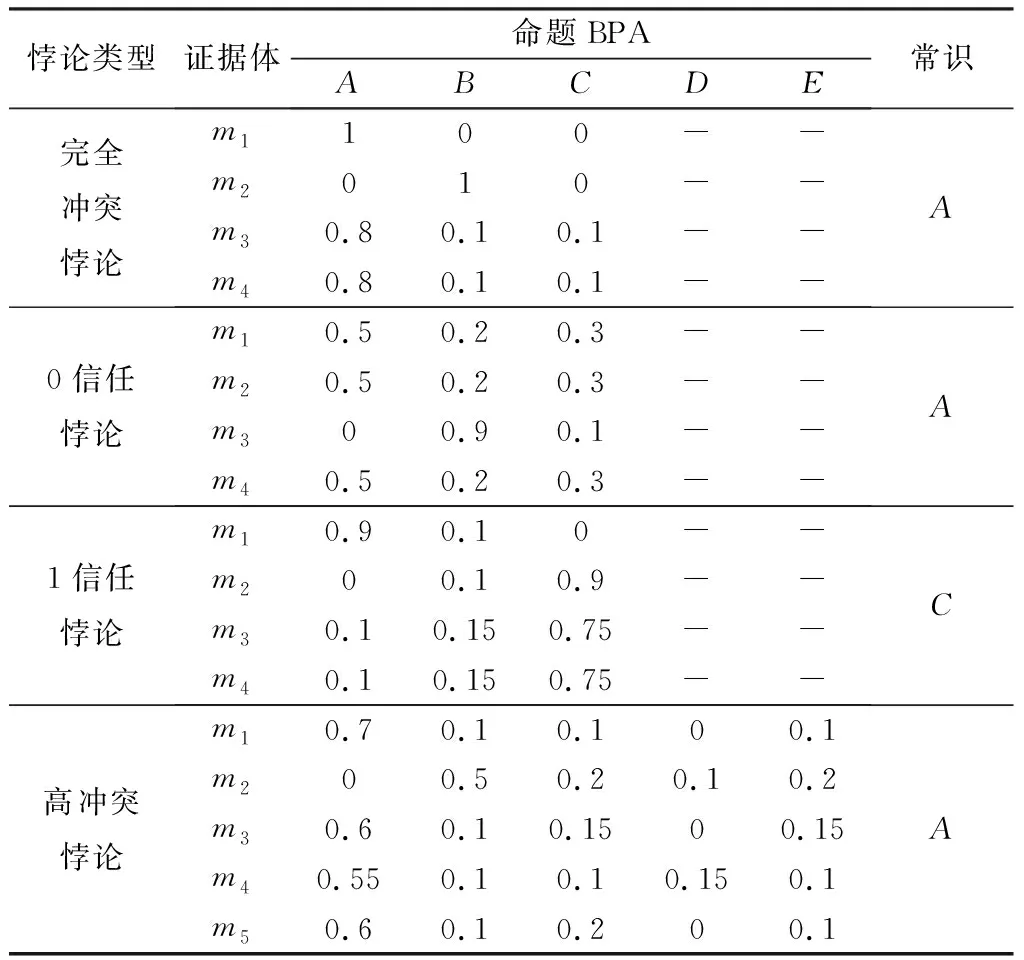
表1 四个常见悖论的BPATable 1 BPA of four common paradoxes

由表2易知，在完全冲突下，D-S证据理论失效、Yager组合规则将冲突完全给全集，认为证据完全无知；孙全等[2]虽有所改善，但全集的BPA仍然很高，不利于实际判断。在0信任悖论下，D-S证据理论和Yager组合规则对A的信任度对0，与实际不符；Sun仍存在全集的BPA仍然过高问题。在1信任悖论下，D-S证据理论、Yager组合规则、Sun仍然存在上述问题。在高冲突悖论下，D-S证据理论、Yager组合规则和Sun仍然存在上述问题。Murphy组合规则[3]、邓勇等[4]和本文方法在四个冲突悖论下都能得到正确的结果，但本文方法具有更高的基本概率分配，收敛更快。实验结果证明了本文方法有效性。

由于本文的不确定性的度量方法参考了文献[12]中的基于定积分的区间距离。因此，使用文献[12]的实验数据，如表3所示，与本文方法进行对比。相比文献[12]，本文综合考虑了证据间的支持度以及证据的不确定度，对冲突的度量较为全面，很大程度上证据信息的缺失；并且本文采用Dempster组合规则对修正后的证据体进行融合计算，较文献[12]采用PCR5组合规则，计算过程更为简单、快速，便于生产实践应用。两个方法的对比结果，如表4所示。

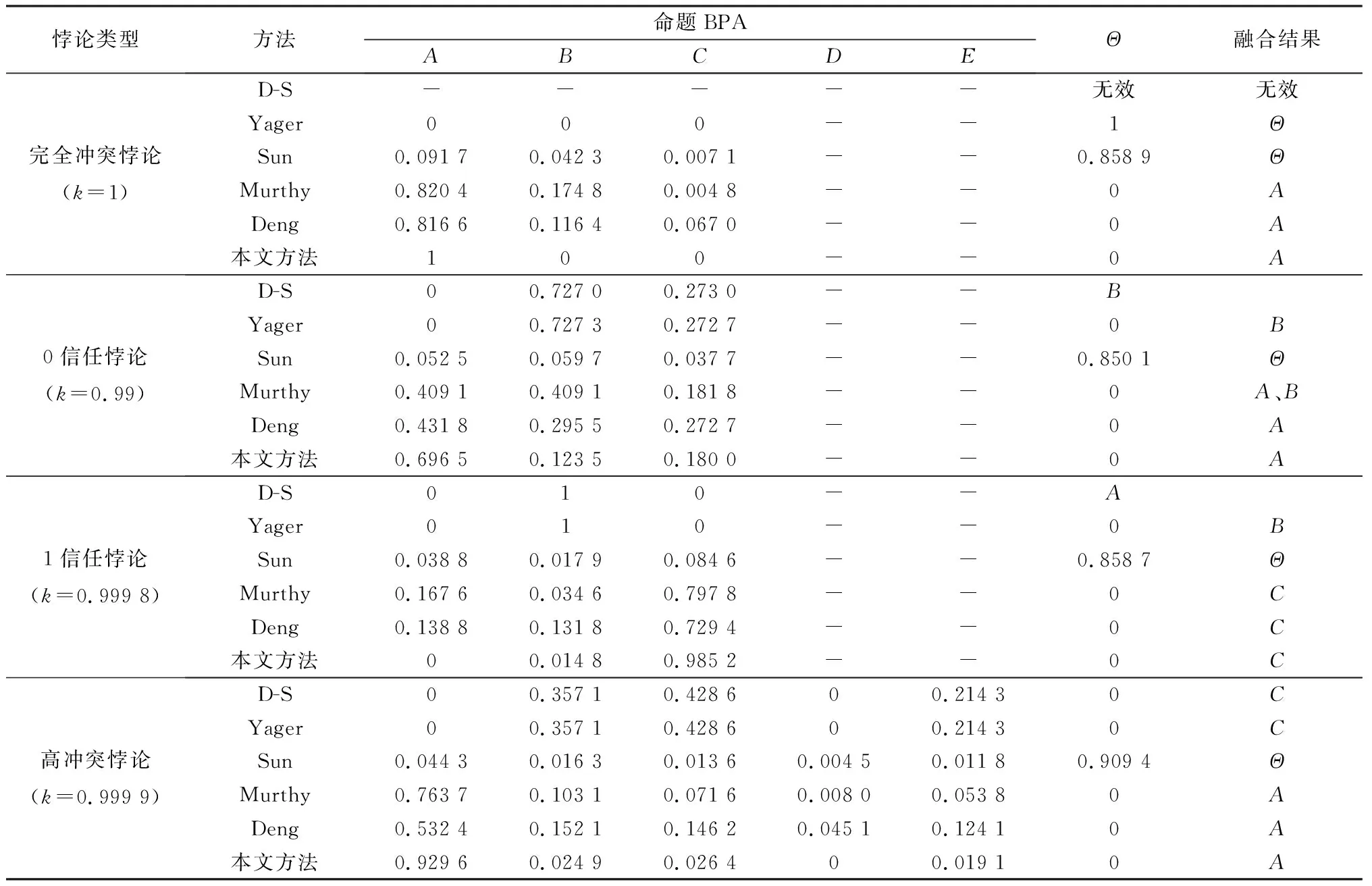
表2 四个常见悖论合成结果Table 2 Four common paradox synthesis results

结果表明，文献[12]和本文方法都能有效地融合证据体。较文献[12]融合结果，本文方法得到的结果具有较高的基本概率分配。

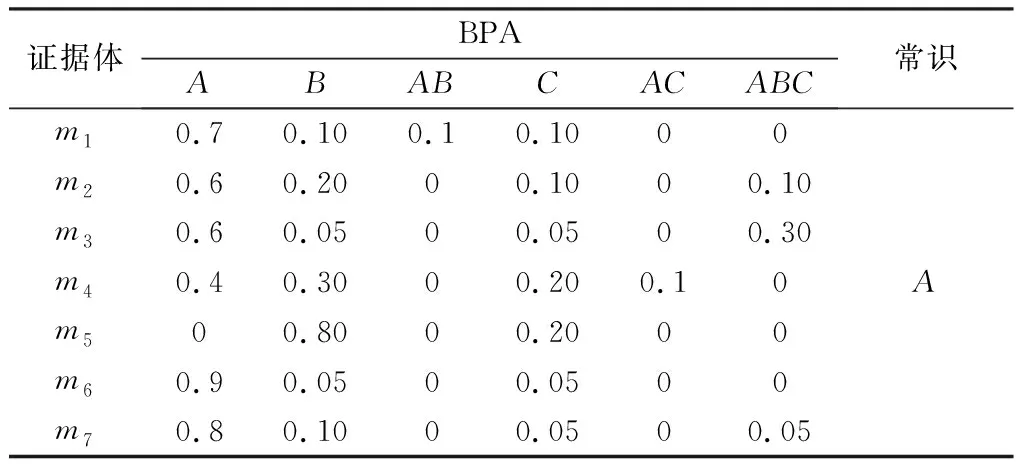
表3 冲突证据体的BPATable 3 BPA of conflict evidence

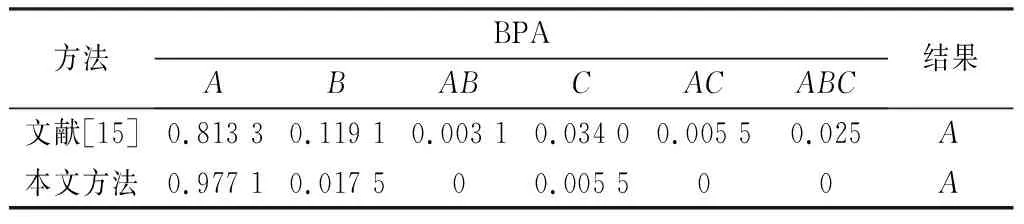
表4 冲突证据体合成结果Table 4 Conflict evidence synthesis results

3 基于改进D-S证据理论的碳/碳复合材料沉积质量预测模型

D-S证据理论以其在不确定推理方面的优势，被广泛应用于许多信息融合系统中，然而如何确定基本概率分配仍是必要环节。考虑到基于正态分布模型的嵌套结构BPA函数[19]无需大量的训练数据集，且没有复杂的计算，方法实现容易；考虑到碳/碳复合材料沉积数据量有限，因此参考文献[19]的方法确定每个测试样本的基本概率分配。结合本文所提出的融合支持度和不确定度的D-S证据理论，构建基于改进D-S证据理论的碳/碳复合材料沉积质量预测模型。为验证所提模型的准确性与实用效果，选取了山西省中电科新能源技术有限公司沉积数据进行实验。在调查研究其沉积重量影响因素和碳/碳复合材料沉积产品等资料后，结合实地可测数据和邻域粗糙属性约简结果，确定了以沉积时间、炉内温度、甲烷流量，氮气流量，耗电量，装炉位置等共6个属性，作为碳/碳复合材料沉积质量的特征因素，将量化之后的单位沉积质量作为碳/碳复合材料致密性的评价指标。随后，收集碳/碳复合材料不同的沉积工艺数据，建立质量预测样本数据库。

在本节中，利用第二节中所提的方法构建一个基于改进D-S证据理论的碳/碳复合材料沉积质量预测模型。模型框架如图2所示。首先，将碳/碳复合材料相关的某个数据集，分为训练集和测试集；然后，使用文献[19]提到的基于正态分布模型的BPA函数，获取每个属性对于每个测试样本的BPA；值得注意的是，为了避免高冲突问题的产生，文献[19]采用嵌套结构来构建BPA函数，但是这一定程度上加大了冲突证据对于结果的影响。因此，本文将归一化的结果直接作为各焦元的BPA，避免了这一问题，并且本文提出的融合支持度和不确定度的D-S证据理论能够很好的融合冲突证据，无需在确定BPA的时候避免冲突的出现。其次，对每组BPA使用本文提出的基于支持度和不确定度的冲突证据融合方法，对每组BPA进行折扣修正并得到融合结果；最后，将最大值对应的焦元作为最终碳/碳复合材料沉积质量预测结果。

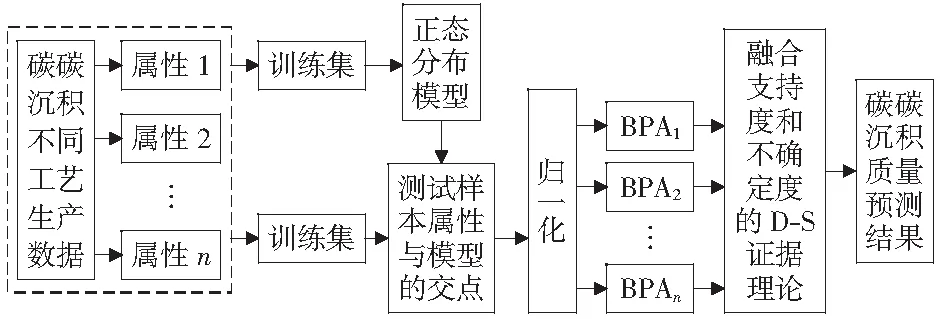
图2 模型框架图Fig.2 Model framework diagram

在本节中，选取部分样本作为测试样本，以验证模型的有效性。限于篇幅，表5仅列出5组典型样本，其中，标签列中的“1”表示样本不合格，“2”表示样本合格。

根据训练集建立正态分布模型后，测试样本通过基于正态分布模型的嵌套结构BPA函数得到每个属性的基本概率分配，每个样本得到n个证据，其中，n为属性个数。因为每个属性对于样本的预判有合格和不合格两种情况，因此每条证据有两个焦元。所得的BPA函数，如表6所示。

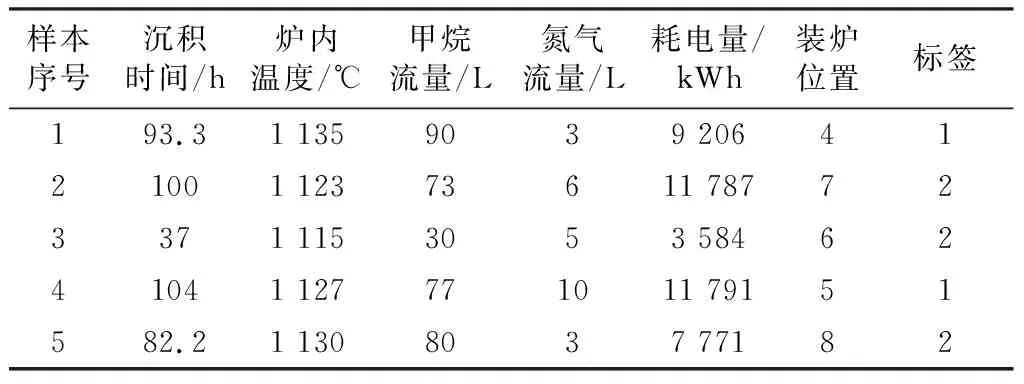
表5 典型样本Table 5 Typical sample

观察表6发现，若以各属性BPA函数中最大值对应的标签，作为第一次的预测结果，则预测结果存在一定概率的误判。如样本3中，甲烷流量出现了误判的情况；样本5中，耗电量、装炉位置两个属性都出现了误判的情况。因此，应用单一属性进行质量预测存在较大的不确定性。而将多个属性的基本概率分配作为融合支持度和不确定度的D-S证据理论的赋值进行融合，最终预测结果正确率则有很大提高。在应用融合支持度和不确定度的D-S证据理论的过程中，使用新的折扣系数对冲突证据的占比进行调整，同时引入不确定信息，更加接近和符合实际生产情况。经新的折扣系数修正后的基本概率分配，如表7所示。

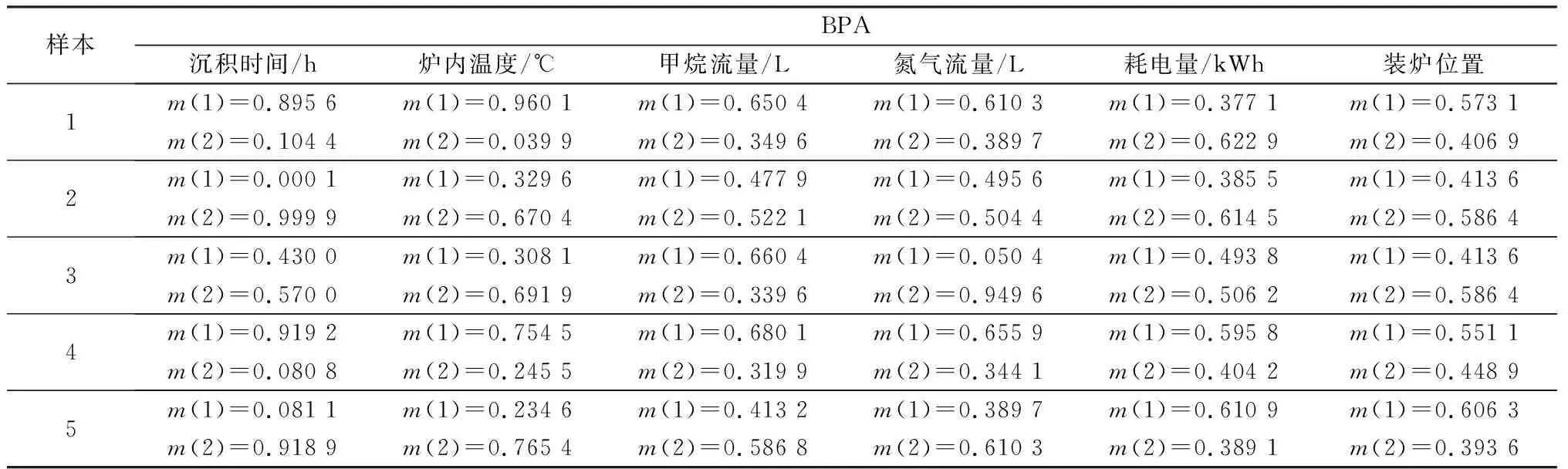
表6 典型样本的BPATable 6 BPA for typical samples

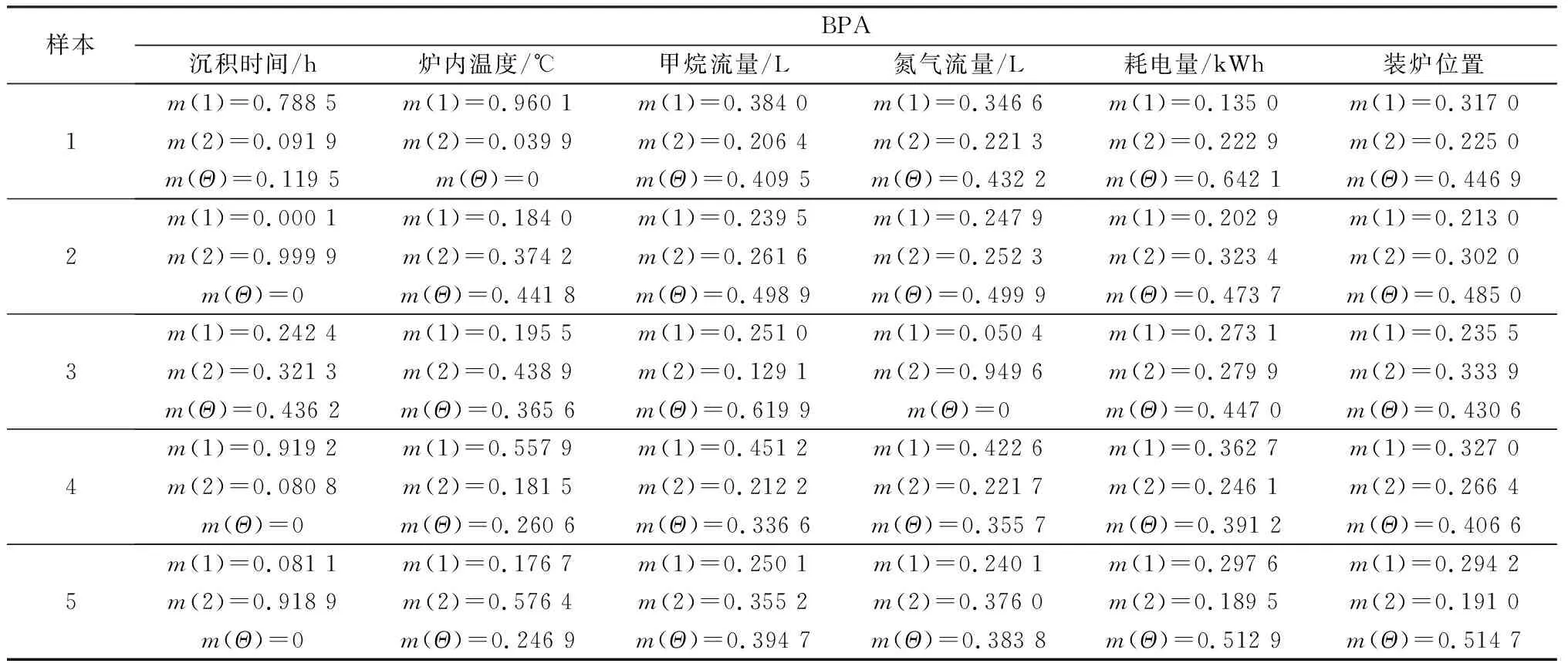
表7 典型样本BPA修正结果Table 7 Typical sample BPA correction results

观察表7发现，每个样本冲突证据的BPA函数值减小，证据体的冲突程度得到了一定程度的削减。经Dempster组合规则融合后的结果，如表8所示。对比测试样本的实际标签，模型的预测结果正确，证明了基于改进D-S证据理论的碳/碳复合材料沉积质量预测模型的有效性。

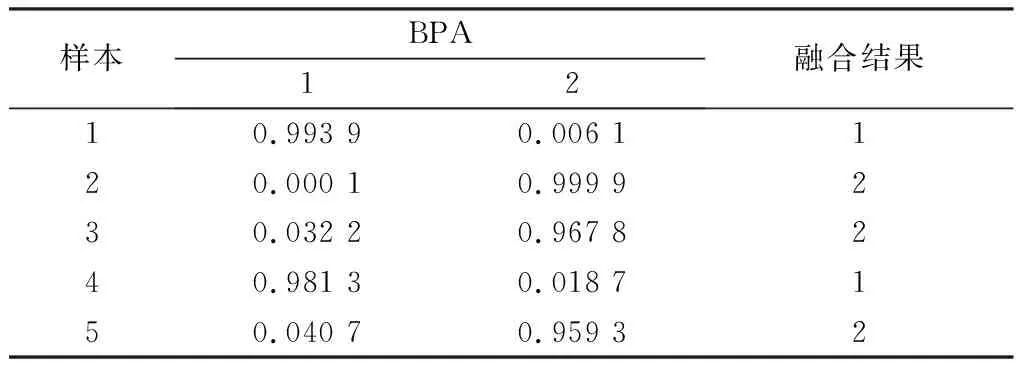
表8 典型样本预测结果Table 8 Typical sample predictions

由于不同的沉积工艺有相应的生产工序，而每个生产工序的致密度不同，所以对不同生产工序的数据进行实验分析，表9为整理的生产工序的数据集信息。

表9 生产工序的数据集信息Table 9 Data set information for production operations

采用十折交叉验证，对比怀卡托智能分析环境[19](Waikato environment for knowledge analysis，WEKA)中的支持向量机、K近邻、决策树、随机森林等经典分类器以及文献[19]的模型，结果如表10所示，预测模型准确率提高了5%～13%，证明了所提模型的有效性。

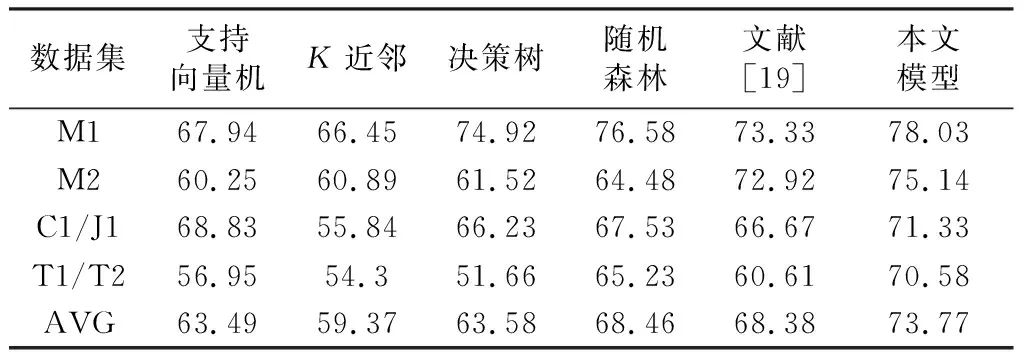
表10 不同方法的预测准确率Table 10 Predicts the accuracy of different methods %

4 总结

本文从证据间支持度和各证据不确定度的角度对D-S证据理论存在的证据冲突问题进行改进，并建立了基于改进D-S证据理论的碳/碳复合材料沉积质量预测模型。实验对比主要结论如下：

1) 引入Spearman相关性限制，并对其进行改进，使之取值范围限制在[0,1]，为后续将其用于具有取值限制的相关算法提供了参考。

2) 对冲突证据体进行二次修正，并将第一次修正后组合结果的置信区间作为证据不确定度量的参考，充分发挥了度量方式的优势，为区间信度研究提供了新的思路。

3) 与经典改进算法和引入基于定积分区间距离改进的算法相比，本文算法能有效地融合冲突证据，并且都表现更高的基本概率分配。

4) 建立了基于改进D-S证据理论的碳/碳复合材料沉积质量预测模型，结果表明，综合考虑证据间的支持度和各证据的不确定度将提高决策的准确性。