盾构下穿高速铁路路基与隧道的变形传递机理及特征研究

林家桢, 黄智海, 彭华, 索晓明, 肖骁骐, 李子晨

（1.中国铁路设计集团有限公司 城市轨道交通事业部, 天津 300308；2.北京交通大学 土木建筑工程学院, 北京 100044；3.中国铁路设计集团有限公司, 天津 300308；4.北京交通大学 轨道结构保护技术研究所, 北京 100044）

0 引言

截至2021年12月31日, 全国高速铁路运营里程突破4万km[1］。随着我国地铁建设中盾构工法的广泛使用, 盾构隧道穿越既有高速铁路的案例越来越多。许多学者对盾构隧道下穿高速铁路的变形特征以及变形传递进行了研究。康直[2］以某地铁下穿高速铁路隧道工程为背景, 利用有限元方法研究发现地铁与高速铁路隧道垂直距离及地铁施工顺序对既有高速铁路隧道的变形有显著影响。杨成永等[3］基于傅里叶级数法进行参数分析, 结合理论方法、数值模拟方法及实测数据对比, 发现轨道变形、内力和脱空范围均随隧道隆起量的增大而增大。高利宏[4］依托某新建双线盾构隧道近接下穿既有盾构隧道工程, 通过有限元软件进行数值模拟, 发现在距离维度上, 隧道结构变形随着距穿越中心距离减小而增大；时间维度上, 穿越时隧道沉降明显并达到峰值, 特别是穿越开始阶段有较大变形速率。蔡小培等[5］通过建立轨道-路基-土体有限元模型, 分析盾构开挖过程中高速铁路轨道变形特征, 发现盾构开挖面位于线路中心线正下方时, 轨道沉降变形速率、两股钢轨沉降差和钢轨横向位移最大, 通过中心线后其值会逐渐减小。刘士海等[6］依托北京某盾构法隧道斜交下穿既有盾构隧道工程, 基于提出的理论公式及沉降实测数据进行拟合分析发现穿越施工既有盾构隧道变形呈现“双凹槽状”纵向柔性变形特征。

目前研究主要针对隧道结构与轨道本身的变形, 对于变形在隧道与轨道之间的传递规律研究较少。伴随着越来越多下穿高速铁路工程的出现, 对于下穿施工条件下结构与轨道自己的变形差异甚至明显脱空的变形特征是需要着重研究的问题。依托我国5个典型盾构下穿高速铁路的案例, 分析盾构下穿高速铁路结构的变形特征与规律, 并针对不同地层、不同结构形式、不同轨道板型式进行参数敏感性分析, 总结下穿引起的沉降变形在结构与轨道之间的传递规律以及影响因素, 为盾构下穿高速铁路既有结构工程提供理论支撑和指导。

1 典型案例分析

1.1 案例选取

近年盾构施工穿越高速铁路的工程较多, 根据不同的地层与结构形式选择以下5个工程案例进行分析（见表1）。案例1为石家庄地铁5号线穿越高铁六线隧道工程, 案例2为长沙地铁3号线下穿京广高铁浏阳河隧道工程, 案例3为北京地铁8号线穿越国铁地下直径线工程, 案例4为石家庄地铁4号线穿越高铁U形槽工程, 案例5为北京地铁14号线穿越京津城际铁路路基工程。

1.2 计算模型

依据下穿范围的工程地质条件, 利用有限元软件Midas模拟双线盾构穿越既有铁路结构施工过程, 采用地层-结构模型进行分析, 土体本构选用D-P准则。土体采用solid45实体单元；盾构管片选用C50混凝土, 厚度0.3 m, 实际工程中衬砌是由管片拼接而成, 所以模拟时将对混凝土的刚度按照系数0.85进行折减[7］；矿山法隧道均采用C35混凝土；注浆等代层强度根据类似工程经验按照原状土体弹性模型2倍进行设定；CRTSⅡ型板式无砟轨道钢轨与轨道板之间的扣件和轨下胶垫等联结件, 忽略其非线性因素, 等效为一个线性弹性件, 采用弹簧-阻尼单元进行模拟, 轨道板与下部支承基础间通过高弹模砂浆进行黏结[8］。注浆等代层示意见图1, 轨道结构见图2。

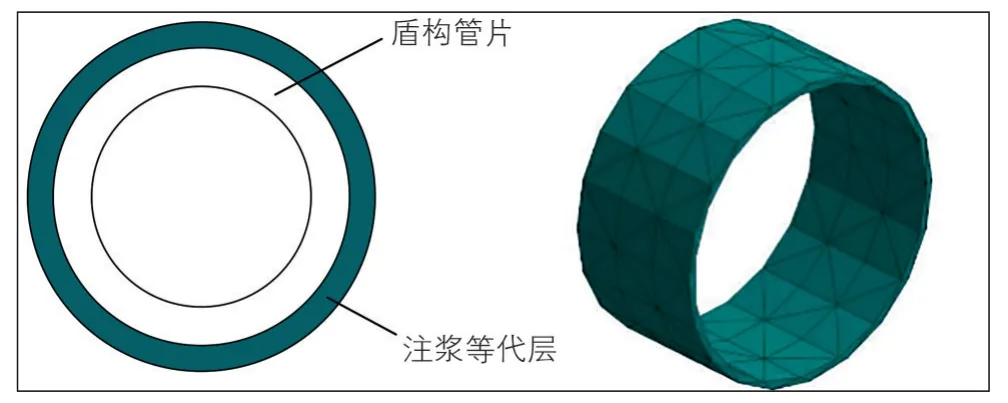
图1 注浆等代层示意图

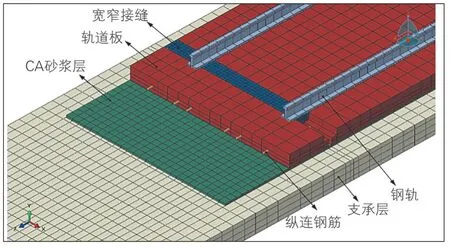
图2 CRTSⅡ型板式无砟轨道模型

考虑到尺寸效应引起的计算误差, 计算案例的边界取值为：左右边界为3倍既有结构宽度, 下边界为1.5倍新建结构高度[9］, 上边界到地表, 取地表（模型的上表面）为自由边界, 模型的四周以及底部取法向约束。工程案例计算模型见图3。

图3 案例计算模型

1.3 计算结果分析

通过建立5个案例（3个隧道和2个路基）的有限元模型, 研究在盾构隧道穿越条件下不同工程案例既有结构变形传递规律, 穿越完成后, 计算结果见表2。

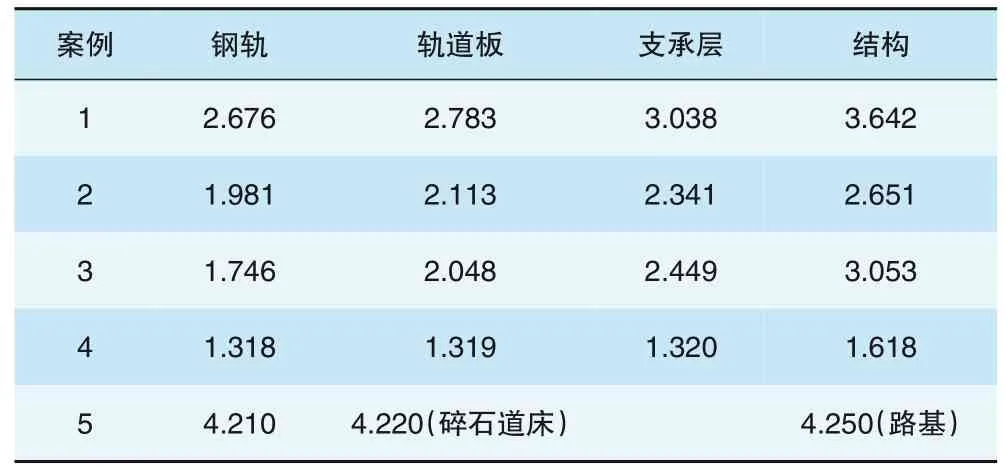
表2 各工程案例既有结构变形计算结果 mm

5个案例在各自条件下穿越对既有高速铁路的变形影响均满足相关安全要求[10］, 其中工程案例2、3、5已经实施完成, 将实际监测最大变形与模拟计算值对比见表3。

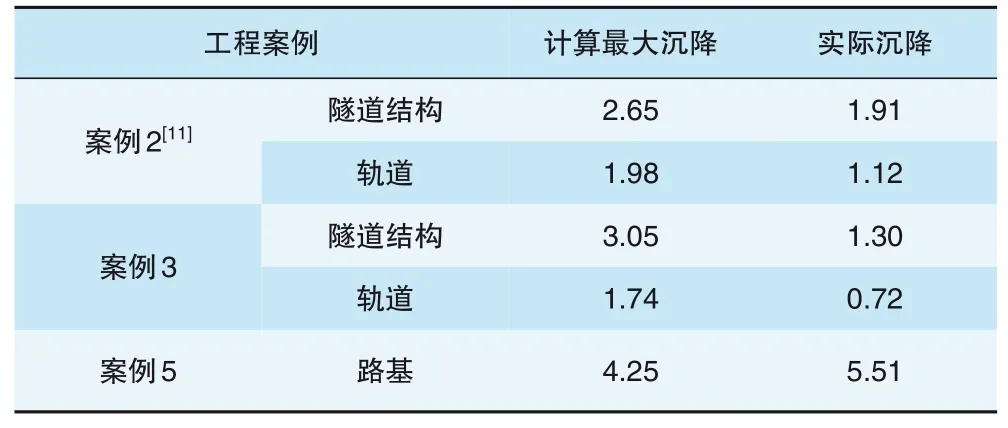
表3 计算变形与实际比对 mm

国铁地下直径线隧道底板变形与轨道变形存在明显差异（＞1 mm）；主要由于下穿净距较小, 沉降槽影响范围小。穿越净距越大, 对既有隧道的影响范围越大, 结构与轨道之间的差异沉降越小。

U形槽隧道结构刚度相对较小, 结构底板与轨道变形差异相对较小；14号线穿京津城际高速铁路碎石道床, 计算路基沉降与轨道道床沉降基本一致。

5个案例中结构与轨道差异变形规律基本一致, 差异变形主要发生在结构与支承层之间, 占最大差异变形的60%以上。

根据已施工完成的3个案例的隧道结构与轨道监测数据, 实际监测数据小于模拟值, 该差异主要由于实际盾构施工过程中会根据监测数据采取一系列控制措施, 此部分措施在模拟中未考虑所致, 但结构与轨道的沉降差异值规律与模拟计算规律基本一致, 验证了计算模型的准确性。由于隧道刚度的差异, 在工程案例3盾构隧道条件下计算轨道变形与隧道变形差异值为1.31 mm, 工程案例2明挖隧道结构条件下计算轨道变形与隧道变形差异值为0.67 mm。

2 参数敏感性分析

为进一步分析不同穿越条件下盾构隧道施工对沉降变形传递的规律, 对不同地层条件、不同既有结构类型和不同轨道类型3种关键参数进行了敏感性分析。

2.1 不同地层条件

选择案例1的明挖法隧道结构为研究对象, 轨道结构形式为CRTSⅡ型板式无砟轨道, 建立地层参数研究模型（见图4）, 通过改变穿越位置土层2土体力学参数, 以此研究不同地层条件下的变形规律。

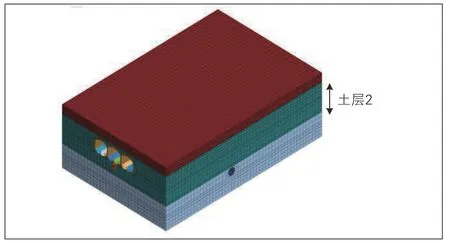
图4 不同地层参数计算模型示意图

参考《工程地质手册》第5版, 结合全国常见地层, 归纳选择卵石、砂土、黏土和淤泥质土4种典型地层作为不同地层敏感性参数。选用的土层分类参数见表4。

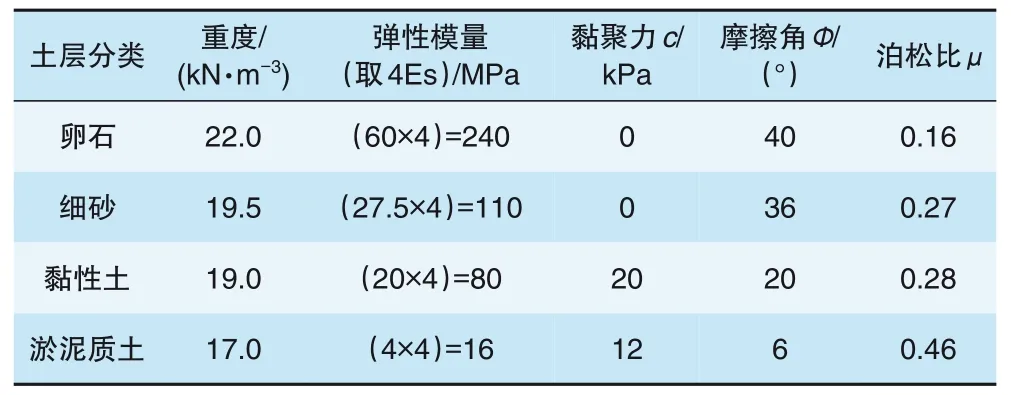
表4 地层分类参数

通过数值模拟计算, 可以得出不同地层条件下盾构穿越施工引起的既有结构变形情况, 不同地层条件下既有隧道结构沉降曲线见图5, 不同地层条件下轨道与结构之间沉降差异见图6。

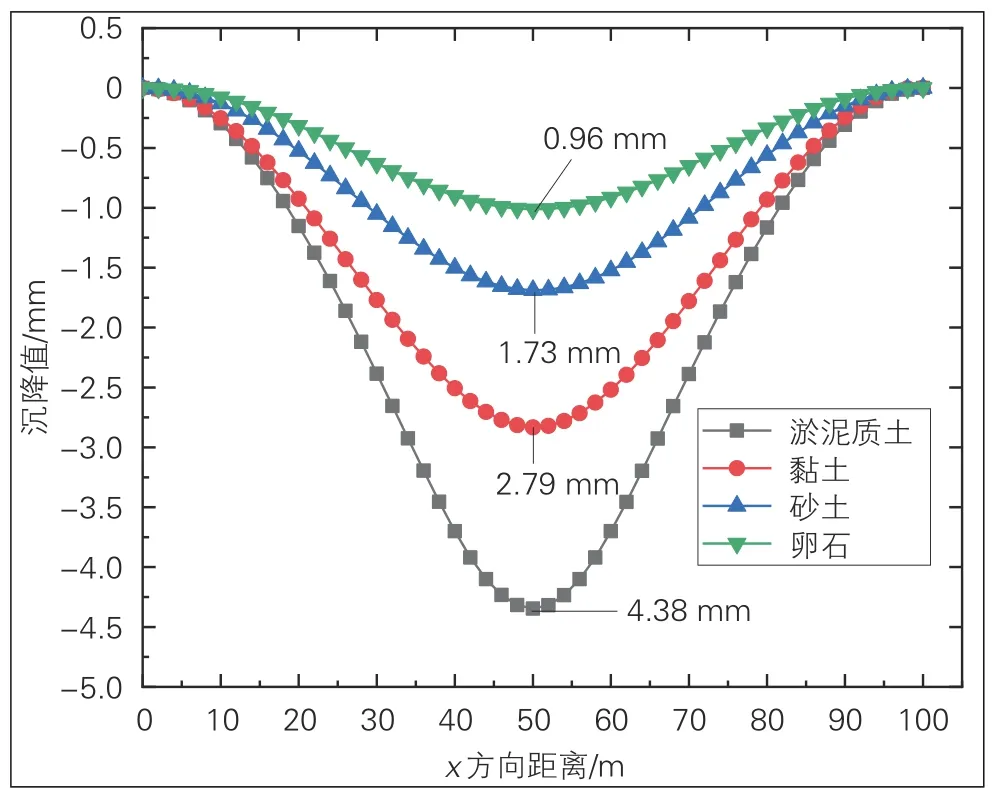
图5 不同地层条件下既有隧道结构沉降曲线

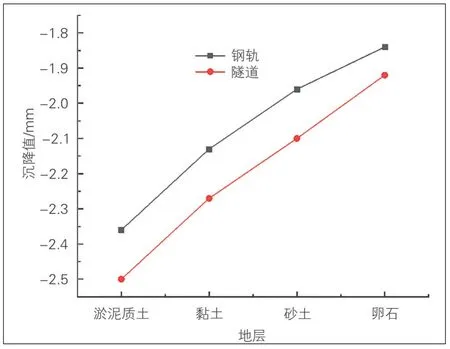
图6 不同地层条件下轨道与结构之间沉降差异

根据不同穿越地层参数的分析, 可知最大沉降值的总体规律是随着土层参数增大逐渐减小, 减小量主要由土层模量值决定。卵石地层条件下隧道沉降为0.96 mm, 淤泥质土条件下隧道沉降为4.38 mm；随着土层参数变化, 结构沉降槽宽度有略微变小的趋势（80~60 m）。穿越地层参数条件主要影响隧道沉降绝对值, 卵石地层条件下结构与钢轨之间差异变形0.12 mm, 4种地层条件下对隧道-轨道的变形传导规律无明显影响。

2.2 不同结构形式

为了研究不同的基于结构形式参数的影响问题, 选取具有代表性的明挖法隧道（案例1）、盾构法隧道（案例3）和路基U形槽（工程案例4）结构形式, 在相同的地层和工程穿越位置关系条件下进行详细研究, 既有结构内部轨道结构形式为CRTSⅡ型板式无砟轨道, 新建与既有结构净距统一取10 m, 以新建与既有结构90°单线正交穿越。不同结构形式变形曲线见图7。

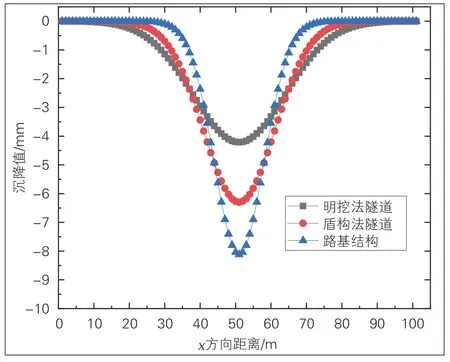
图7 不同结构形式变形曲线

在施工模拟计算中, 明挖法隧道结构的沉降最大值为4.213 mm, 纵断面沉降槽宽度为70 m；盾构法隧道结构的沉降最大值为6.375 mm, 纵断面沉降槽宽度为48 m；路基结构的沉降最大值为8.421 mm, 纵断面沉降槽宽度为25 m。U形槽、盾构、明挖隧道结构刚度依次递增, 随着隧道结构刚度逐渐增加, 在相同沉降条件下, 传递至钢轨的竖向变形逐渐增加, 盾构隧道与U形槽的钢轨差异变形较明挖法隧道增大约25%, 相同结构形式条件下, 沉降越大, 轨道与结构之间的差异变形随之增加。变形传导过程中, 最大的差异变形均发生在隧道结构与轨道板支承层之间, 总差异沉降占比约为60%~85%。

2.3 不同轨道结构类型

选取案例1中的明挖法隧道计算模型, 改变隧道内部的轨道结构形式（CRTSⅡ型和CRTSⅢ型）, 其中CRTSⅢ型板式无砟轨道主要由钢轨、扣件、预制轨道板、配筋的自密实混凝土（自流平混凝土调整层）、限位挡台、中间隔离层（土工布）和钢筋混凝土底座等部分组成, 轨道结构为单元分块式结构。CRTSⅢ型板式无砟轨道模型采用接触单元来模拟自密实混凝土和底座板水平接触间的土工布、自密实混凝土凸台四周与底座板凹槽间弹性橡胶垫层, 前者法向采用硬接触, 切向摩擦系数取0.7, 后者接触刚度为0.1 GPa[12-13］。CRTSⅡ型板式无砟轨道模型示意见图8, CRTSⅢ型板式无砟轨道模型示意见图9。

图8 CRTSⅡ型板式无砟轨道模型示意图

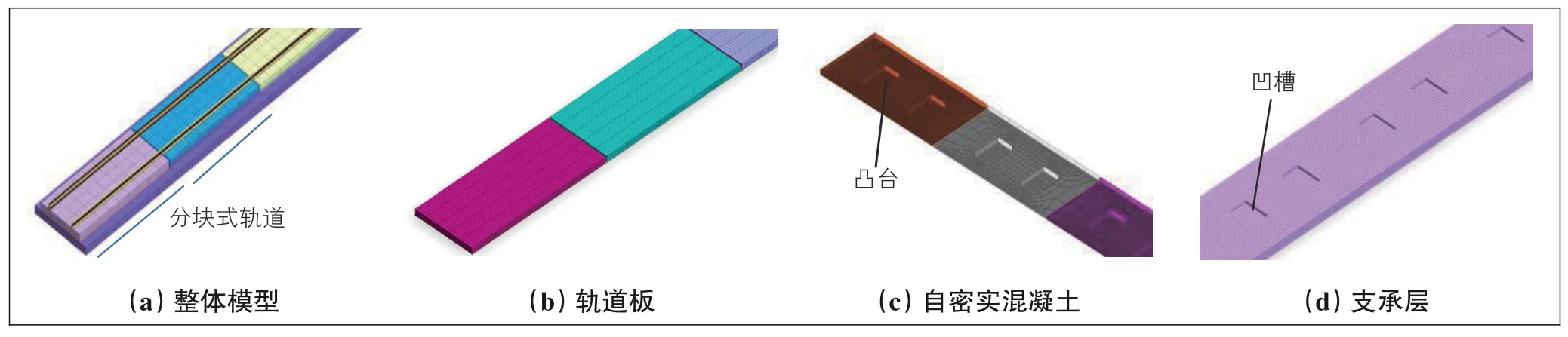
图9 CRTSⅢ型板式无砟轨道模型示意图

通过在隧道底部施加不同强制位移工况（-5、-10、-15、-20 mm）, 研究隧道内不同轨道结构形式的变形传递规律。2种轨道结构在不同位移工况下的变形曲线见图10。

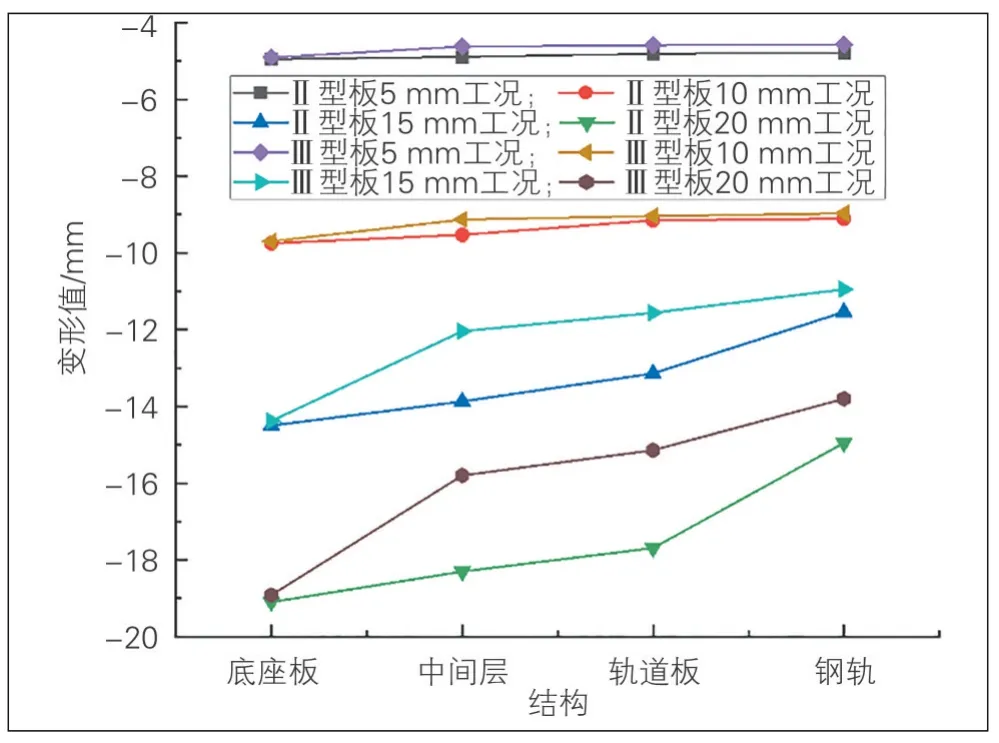
图10 CRTSⅡ型与CRTSⅢ型板式无砟轨道在不同位移工况下的变形曲线

由于CRTSⅡ型板式无砟轨道是整体浇筑纵连结构, CRTSⅢ型板式无砟轨道为分块式结构, 在相同结构变形条件下, CRTSⅡ型板式无砟轨道的轨道变形小于CRTSⅢ型板式无砟轨道。结构沉降在10 mm以下时, CRTSⅡ型板式无砟轨道与CRTSⅢ型板式无砟轨道对轨道变形传导差异不明显（＜5%）, 随着结构沉降增加, 差异逐渐增加, 最大沉降20 mm时, 差异值达到1.1 mm。无砟轨道的变形传递主要发生在底座板与中间层之间。

3 结论

针对多个典型盾构穿铁路工程案例, 采用数值模拟的计算方法建立地层-结构、无砟轨道-隧道/路基耦合模型等静力模型, 研究了盾构下穿高速铁路路基、隧道的穿越变形规律以及变形传递规律, 对比已有的项目监测数据得出结论如下：

（1）国铁地下直径线隧道底板变形与轨道变形存在明显差异（＞1 mm）；主要原因是由于下穿净距小, 沉降槽影响范围小。穿越净距越大, 对既有隧道的影响范围越大, 结构与轨道之间的差异沉降越小。

（2）隧道刚度越大, 相同条件下轨道与结构的差异变形就越小。案例2与案例3最大沉降值相当条件下, 由于盾构隧道刚度相对较小, 案例3结构与轨道之间的变形明显大于工程案例2；U形槽隧道由于存在变形缝结构刚度相对较小, 结构底板与轨道变形差异相对较小；碎石道床计算路基沉降与轨道道床沉降基本一致。

（3）随着不同类别隧道结构刚度逐渐增加, 在相同沉降条件下, 传递至钢轨的竖向变形逐渐增加, 盾构隧道与路基U形槽的钢轨差异变形较明挖法隧道增大约25%, 最大的差异变形均发生在隧道结构与无砟轨道支承层之间, 总差异沉降占比约为60%~85%。

（4）不同地层条件主要影响穿越后隧道结构的最大沉降值, 沉降值随着土层模量参数增大逐渐减小, 不同地层条件对隧道-轨道的变形传导规律无明显影响。

（5）在相同结构变形条件下, CRTSⅡ型板式无砟轨道的轨道变形小于CRTSⅢ型板式无砟轨道。结构沉降在10 mm以下时, CRTSⅡ型板式无砟轨道与CRTSⅢ型板式无砟轨道对轨道变形传导差异不明显（＜5%）, 随着结构沉降增加, 差异逐渐增加, 最大沉降20 mm时, 差异值达到1.1 mm。2种无砟轨道变形传递主要发生在底座板与中间层之间。