Natural convection effects on TNT solidification inside a shaped charge mold
Çi˘gdem Susantez ,Ald′elio B.Caldeira ,Bruna R.Loiola
a Trakya University,Engineering Faculty,Mechanical Engineering Department,Edirne,22030,Turkey
b Management and Technological Innovation Agency,Brazilian Army,Rio de Janeiro,23020-470,Brazil
c Military Institute of Engineering,Mechanical Engineering Department,Rio de Janeiro,22290-270,Brazil
Keywords:Solidification Natural convection Explosive Dimensionless model Anti-Tank ammunition
ABSTRACT High Explosive Anti-Tank(HEAT)warheads and ammunitions are frequently produced by explosive casting inside an axis-symmetric mold with an inverted conical geometry in the basis.In order to prevent manufacturing defects,the solidification process must be controlled.In this study,a dimensionless solidification model has been proposed to investigate the heat transfer considering the natural convection inside the liquid explosive and the numerical simulations were performed by using COMSOL Multiphysics and Modeling Software,employing trinitrotoluene(TNT)thermophysical properties.The effect of three different boundary conditions on the top of the mold have been evaluated:convection,adiabatic and isothermal.It has been observed that solidification process was faster for convection case and slower for isothermal case,while an intermediary total solidification time value was found for adiabatic case.Moreover,liquid explosive was completely surrounded by solid explosive during the solidification process for convection case and also for adiabatic case through the end of the process.Otherwise,it was not observed for isothermal case.The natural convection effects promoted a vortex inside the liquid explosive,accelerating the heat transfer process.It has been concluded that isothermal mold top boundary condition should be preferred to prevent manufacturing defects,avoiding high thermal stress.
1.Introduction
Explosives are processed by techniques of casting,extrusion and pressing[1].If the solidification process could not be controlled properly,internal defects occur during casting such as air entrapment during filling of the material,and porosity formation due to shrinkage[2].As the main factor of the ammunition premature explosion is the pore formation inside the explosive[3],solidification process should be controlled properly.Manufacturing defects are highly related to the thermal stress due to the rapid temperature change and large temperature gradients inside the domain.
Experimental investigations about solidification of explosives are dangerous and expensive.In this sense,analytical and numerical methods have been used taking into account potential issues.Although Neumann's analytical solution is generally useful for one dimensional problems,numerical methods such as enthalpy method,effective heat capacity method and apparent heat capacity method are mostly used for complex geometries[4,5].
Buoyancy effects were neglected for the solidification of the explosive in many studies in the literature.Chen and Shiuan[6]made an experimental and numerical study on the solidification of TNT.They used modified and extended equivalent heat capacity model in their study.Susantez and Caldeira[5]modelled solidification of TNT by apparent heat capacity method.They proposed genetic algorithm optimization method for the‘‘half of phase change temperature range’’and obtained this value as 0.872 K.Caldeira et al.[7]estimated porosity formation during solidification of TNT using particle swarm optimization.In their study,they modelled the problem by effective heat capacity method.Kumar and Rao[8]presented a model based on energy balance at the solid-liquid interface for the cooling and solidification of TNT.In some researches,natural convection effects are considered duringsolidification of the explosive.Ji and Lin[9]used enthalpy method and Darcy law in their solidification model of casting explosives.They concluded that if natural convection effects are taken into account together with heat diffusion,not only temperature distribution is more homogeneous but also solidification time is increased.Sun and Garimella[10]experimentally and numerically investigated the solidification of an energetic material considering convection and volume shrinkage.They used volume-of-fluid method for shrinkage and enthalpy-porosity method for phase change.They also concluded that it is possible to control the solidification shrinkage by improved cooling conditions.
In this study,a dimensionless model for the solidification of an explosive has been proposed for the general usage in phase change problems considering natural convection effects.The model,considering buoyancy force in the liquid region and convection effects on the mushy region,was applied to the solidification process of TNT.The effects of the three different boundary conditions on the top of the mold have been numerically investigated using COMSOL Multiphysics and Modeling Software.
It is noteworthy that the present model does not take into account the formation of defects during solidification.However,this model provides the evolution of the temperature field in the explosive during the solidification process,enabling the identification of positions and times with high temperature gradients,which are related to high thermal stress and,consequently,to defect formation conditions such as porosities,voids and cracks.In this sense,the numerical simulations of the heat transfer during explosive solidification are important to design the mold cooling process,avoiding high temperature gradients inside the explosive in order to prevent solidification defects.
The novelty of this study is the investigation of the effects of the convection,adiabatic and isothermal top boundary conditions on the solidification process and on the phase change front in a typical geometry of a High Explosive Anti-Tank(HEAT)ammunition,furnishing relevant information to the cooling design of the manufacture set up.Moreover,this geometry differs from other studies,which were usually devoted to High Explosive(HE)ammunitions.
2.Material and method
In this research,solidification process of TNT explosive inside the geometry presented in Fig.1 have been investigated numerically under the effect of natural convection and heat diffusion.The geometry is based in a shaped charge device where the explosive is placed in a cavity with a metal cone.When this kind of ammunition hits the target,a detonation wave propagates inside the explosive and impacts on the metal cone,which becomes a liquid jet,moving at a high velocity,able to perforate the target.
The solidification process could be performed under distinct conditions as:letting the explosive solidifying in the mold with the open boundary exposed to the environment;inserting a foam on the open boundary to isolate this surface and preserve heat losses,and last,a hood ventilation system could be used to maintain a specified temperature at this surface.To mimic these processes,three different top boundary conditions have been considered as convection,adiabatic and isothermal.
Navier-Stokes equations in two-dimensional form were considered with the assumption of incompressible fluid.As it has been known that TNT behaves like a Newtonian fluid,under normal industrial conditions[10],molten TNT is assumed to be Newtonian in this work.Boussinesq approximation was applied in z momentum equation with the term of buoyancy force,F.The momentum source terms Sand Sconsider the change in porosity in r and z momentum equations respectively[11].
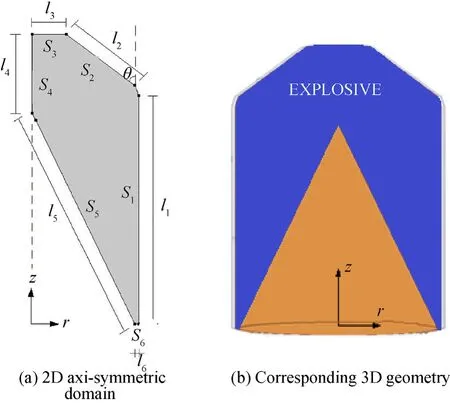
Fig.1.Geometry of the investigated explosive domain.

where u,u,P,T,ρ,c,k,L,fand μ are the velocity components in the r and z directions,pressure,temperature,density,specific heat,thermal conductivity,latent heat,liquid fraction and dynamic viscosity of the explosive,respectively.
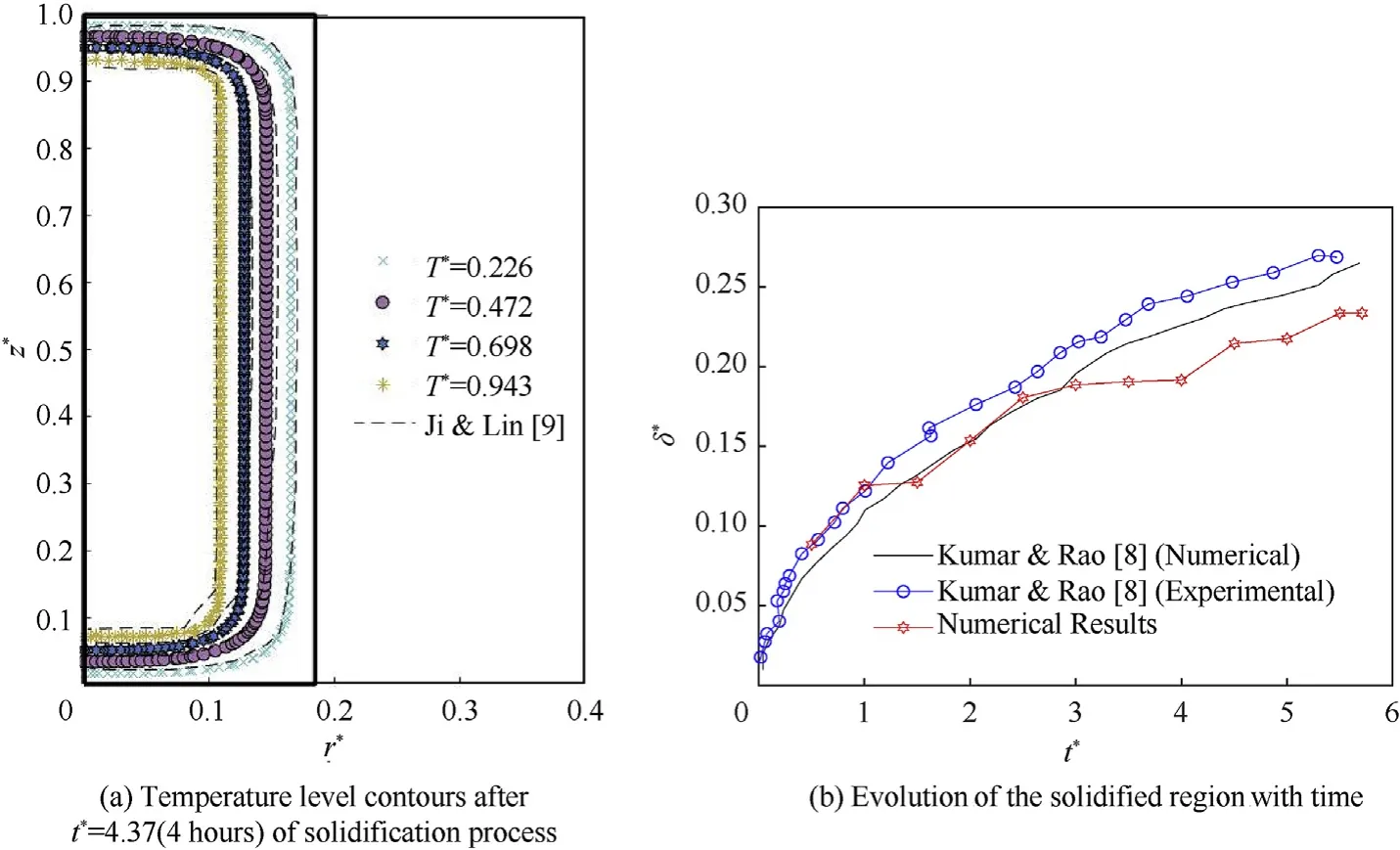
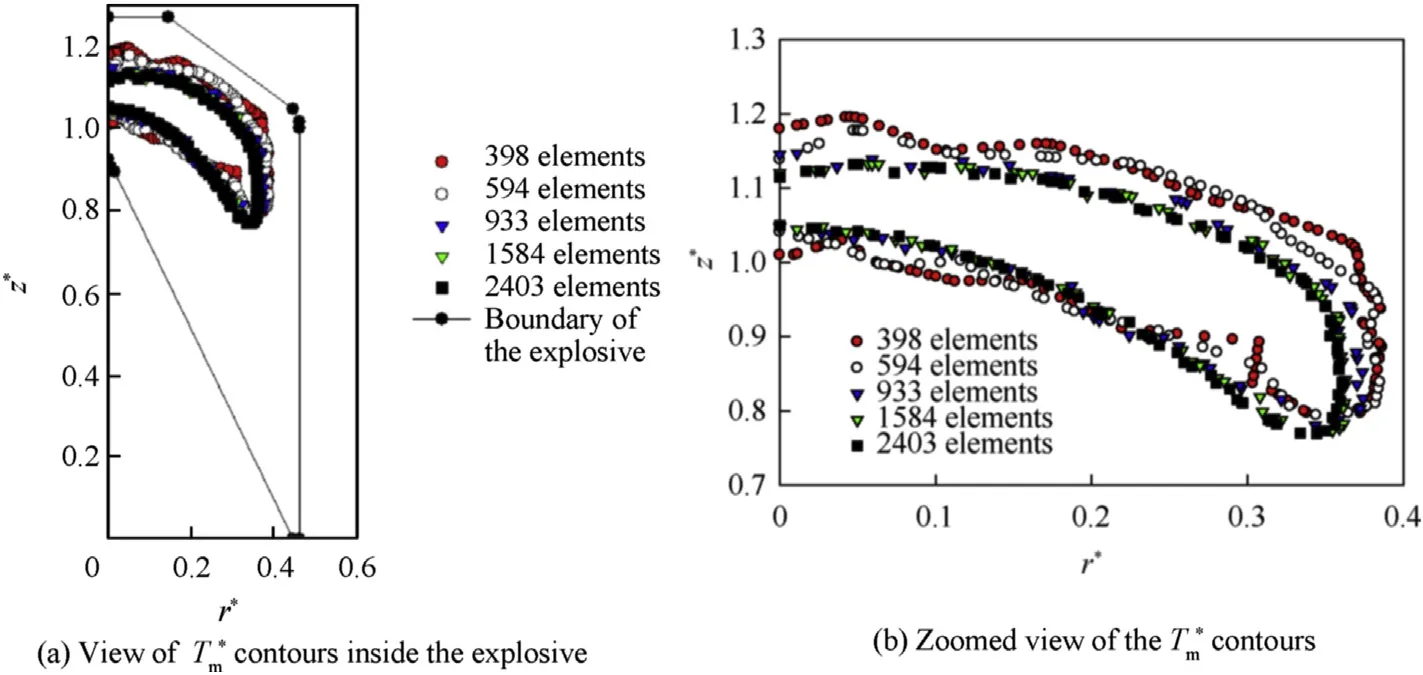
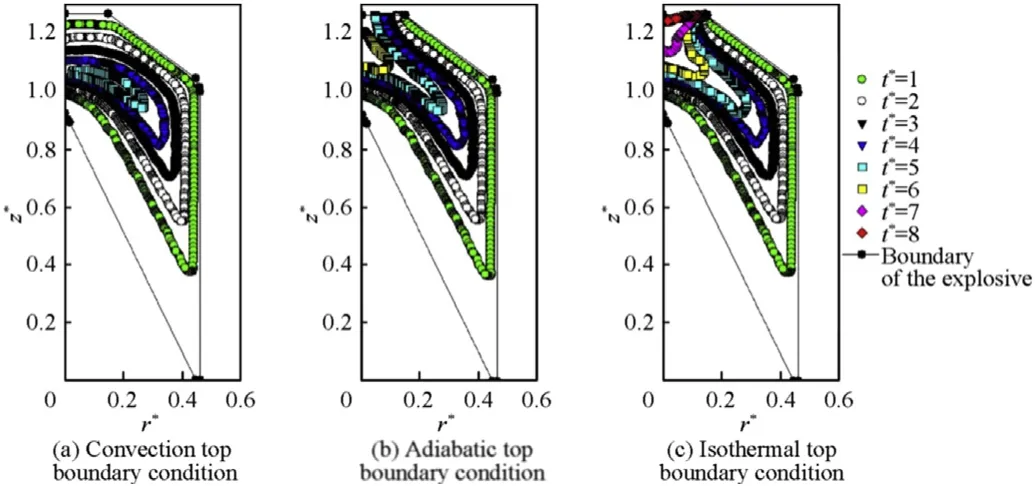
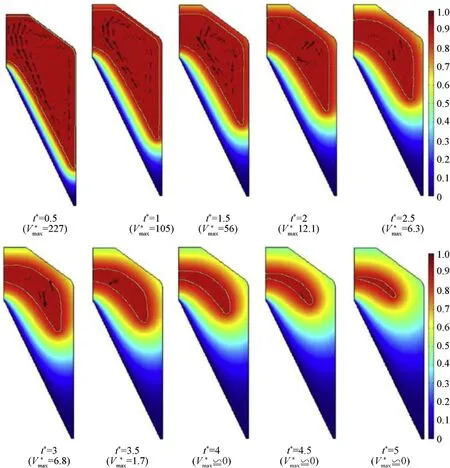
Initial and boundary conditions are given in Eqs.(5)—(10)considering symmetry on the z axis,prescribed temperature to the conical and bottom surfaces and convection at the lateral surfaces.Three different types of boundary conditions(Eq.(7a-c))were considered to the top surface.Non slip conditions were adopted to all surfaces.
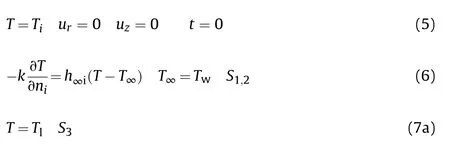
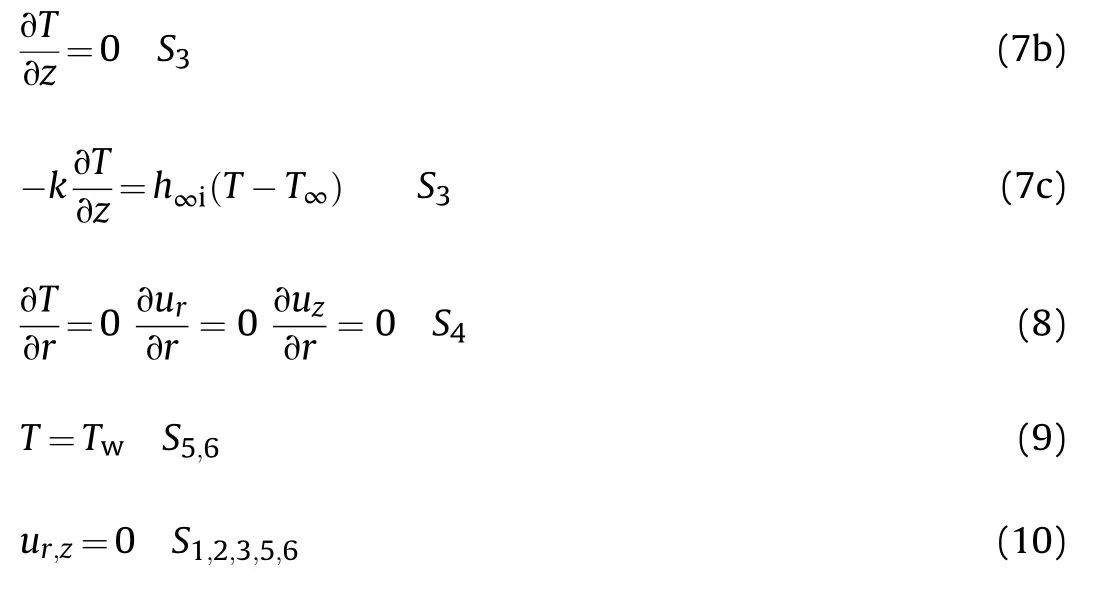
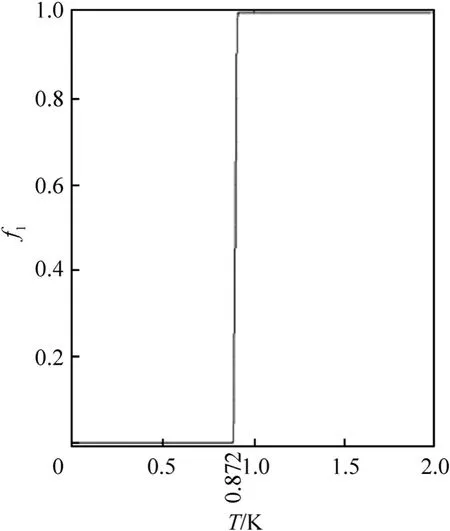
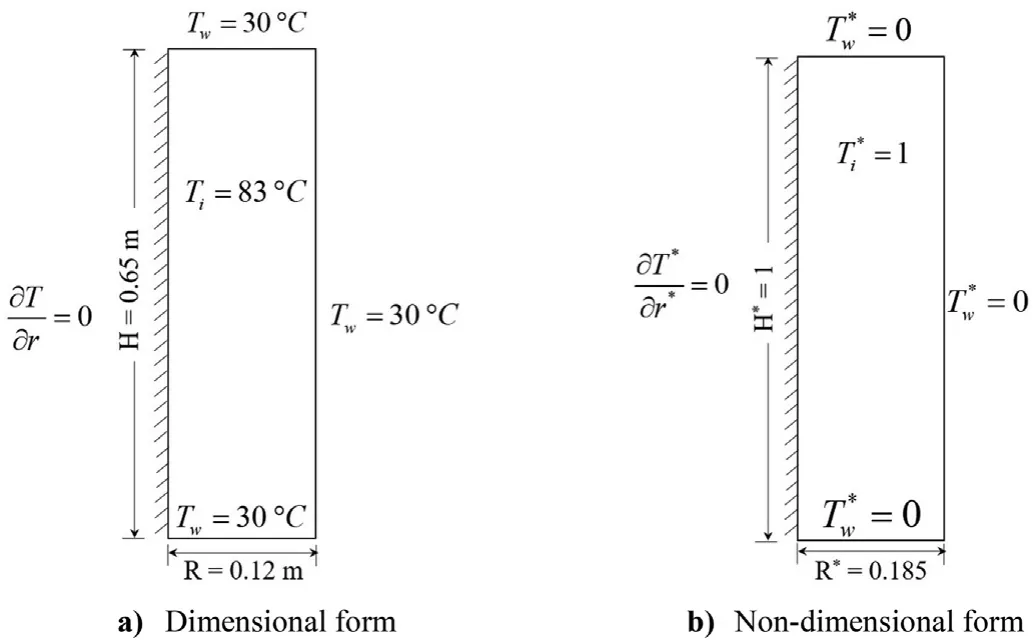
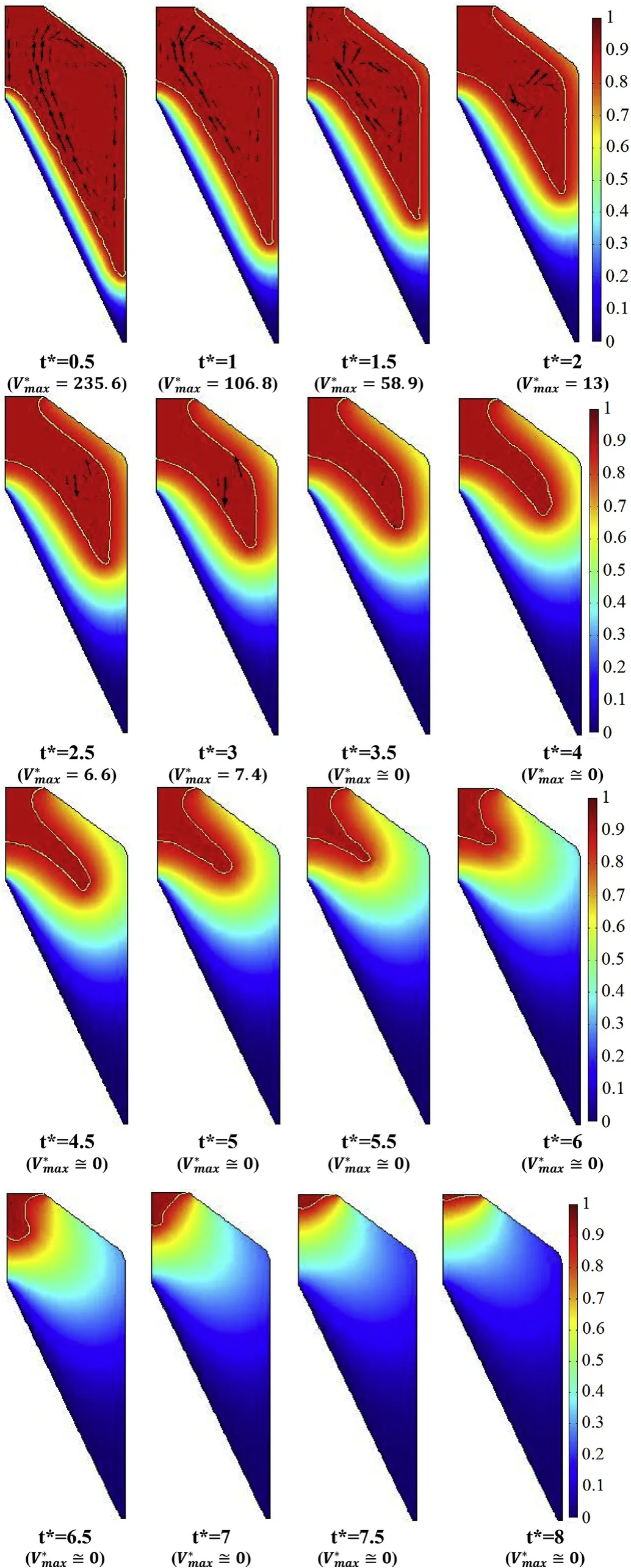
where T,n,h,T,Tand Tare the initial temperature,unit normal direction,heat convection coefficient,temperature of ambient air,liquefication temperature and wall temperature,respectively.Last term in the energy equation will be active if temperature is in the range of mushy region,T where g,βand A(f)are gravitational acceleration(9.81 m/s),volume expansion coefficient of explosive and porosity function[12,13]given at Eq.(14),respectively,which was defined by Brent et al.[12].The terms of sand sare active only in the phase change region or in other words in the mushy region.A(f)was defined in order to make momentum equations to mimic the Carman-Kozeny equations in the phase change region which is treated as porous media[12].The liquid fraction f,in this study,is defined by a smooth function as shown Eq.(15)and its behavior for TNT is presented in Fig.2. whereΔT is the half of the phase change temperature and Tis melting temperature.The parameter C is morphology constant of the melting front,ε is a small constant used to avoid division by zero in the study of Brent et al.[12].In this study,the values of 1.6×10and 10have been used respectively for the constants of C and ε,as used in literature[9]. Fig.2.Smooth form of the liquid fraction f1 for TNT. Dynamic viscosity of the explosive in this model has been modified by defining temperature dependent fluid viscosity[14].In this approximation velocity diminishes by defining very high viscosity value in the solid region.μis the liquid viscosity value when the explosive is in the liquid form. Non-dimensional forms of the governing equations have been obtained by dimensionless variables. where ν is kinematic viscosity of the explosive.Dimensionless forms of the governing equations are given by Eqs.(18)—(21). where Gr is Grashof number,Pr is Prandtl number,s*and s*are the dimensionless forms of the momentum source terms due to the change in porosity,as follows: Non-dimensional forms of initial and boundary conditions are given by Eqs.(24)—(29)with the assumption of air temperature(T)is equal to wall temperature(T). where nis the normal direction in dimensionless form and i is the corresponding index of the surfaces in Fig.1.Bi is the Biot number defined as: Correlations given at Eqs.(31)and(32)have been used for the calculation of the convection heat transfer coefficients on the corresponding surfaces[15].The convection coefficient on the curved surface between surface 1 and 2 was assumed to be h. The work of Ji and Lin[9]was used for numerical verification.In their work,the solidification process of TNT inside a cylindrical shell having 120 mm of radius and 650 mm of height was investigated considering free convection and diffusion during explosive solidification process.The symmetry was considered in the z axis while the other boundaries were maintained at a prescribe temperature.The cylindrical geometry together with the boundary conditions adopted,in dimensional and non-dimensional form,respectively,are illustrated in Fig.3.The Grashof and the Prandtlnumbers used at the simulation are respectively 3˙2663×10and 816.72. Fig.3.Geometry and boundary conditions used at the verification section. The work of Kumar and Rao[8]was used for numerical verification and experimental validation.In their work,experimental and numerical results for the thickness of the solidified region are presented for the solidification of TNT performed under controlled cooling.The geometry of the domain has diameter of 145 mm and height of 270 mm.The initial temperature of the TNT projectile was considered uniform at 90C.The walls were considered with a prescribe temperature(T)of 50C.A heating probe of 106 mm from the top center of the mold was used to guide the solidification front at a prescribe temperature of 90C.Below the probe,a symmetry boundary condition was considered.The corresponding Grashof and the Prandtl numbers for this simulation are respectively 4.08×10and 69.5. In the verification analysis,the dimensionless temperature distribution contours at t*=4.37,which corresponds to 4 h after solidification starts,are compared with the literature results in Fig.4a.3092 elements have been used for the verification.It has been shown that the numerical solution has the same behavior with the numerical study of Ji and Lin[9].In the validation analysis,dimensionless thickness of the solidified region δis presented in Fig.4b and shows a good agreement with experimental and numerical results of Kumar and Rao[8]. Mesh dependency analysis has been performed for the investigated geometry.It has been shown from Fig.5 that time dependent average temperature of the domain does not change with 933 and more elements.But in the solidification processes,movement of the phase change front has major effect on the results.Considering results in Fig.6a and b,2403elements have been used for the analysis in this study. Fig.5.Time dependent average temperature value for different meshes for the case of convection top boundary condition. Thermophysical properties of TNT are presented in Table 1.In this study,thermal property values in solid and liquid phases are considered the same for the numerical analysis.During the cooling process of TNT phase change starts at the liquefication temperature of T,which is equal to T+ΔT and ends at the solidification temperature of T,which is equal to T-ΔT.Volume expansion coefficient of TNT during the phase change has been evaluated as 0.03598 Kwhich is convenient with the literature[9,16].The corresponding dimensionless lengths of the geometry,presented in Fig.1,are also presented in Table 2. Table 1Thermophysical properties of TNT and model parameter[5,9,10,17,18]. Table 2Dimensionless lengths of shaped charge geometry. Fig.4.Verification and validation of the code. Fig.6.Position of Tm*at t*=3.5 for the case of convection top boundary condition. Fig.7.Tm*contours inside the explosive. This study not only shows the effect of distinct cooling processes of the explosive inside a conical shell,but also presents dimensionless model for the solidification process under the effect of natural convection inside the explosive.Fig.7 shows the position of the phase change front evolving with time for convection,adiabatic and isothermal top boundary conditions respectively.It has been shown that for convection top boundary condition the solidification process occurs from the outside to inside having the end of the process in the inner region of the explosive.Similar behavior occurs for the adiabatic top boundary condition at the end of the solidification process.But in this case,solidification process is completed at the region closes to the symmetry axis.For isothermal top boundary condition,the top surface is maintained at the liquefication temperature promoting the ascendant movement of the solidification front. Furthermore,the results shown in Fig.7 indicate the influence of the top boundary condition on the heat transfer.The convection top boundary condition is the most efficient cooling process,removing heat through the top of the mold,consequently,the solidification front in vicinity of the top moves like a plane surface parallel to top boundary from top to down,creating a solidified region on the top.In a different way,the adiabatic top boundary condition provides null heat flux on the top,imposing that the cooling process is controlled by the other mold surfaces.So,in this case,the solidification front evolves inward in radial direction on the top of the mold.On the other hand,the isothermal top boundary condition,since the prescribed temperature is above the melting temperature,keeps a liquid region on this boundary,being a hot region in the domain,supplying heat to the explosive. Temperature simulations with phase change front are also presented on Figs.8—10 for the investigated top boundary cases.The Prandtl and the Grashof numbers in this study respectively are 53.09 and 6.7×10,which corresponds to the initial temperature of 360 K and constant wall temperature of 300 K considering the length of l=13 cm.Vortex formation is observed at the beginning of the process.It has been understood from the maximum value of the dimensionless velocity of Vthat generally,convection forces decrease as solidification proceeds and become ineffective at the end of the solidification. Fig.8.Temperature simulations for the convection top boundary condition. The reduction of the natural convection forces with time inside the explosive is explained by the reduction of the temperature gradient inside the liquid,which is combined with the reduction of the amount of liquid.As time evolves heat is transferred from the liquid region to the solid region,decreasing the temperature gradient inside the liquid.In addition,the liquid has a limited heat source capacity linked to the liquid amount of mass and temperature,this capacity degrades with time. It has been also observed from temperature simulations that solidification is faster for the convection top boundary condition.Unsolidified region enclosed by solid phase is observed at the middle of the explosive for this case.This is not a desired case,because faster solidification process causes higher thermal stresses and gap formation may be observed.Comparing with previous case,the solidification process takes longer time for the case of the adiabatic top boundary condition.Unsolidified region enclosed by solid phase has also been observed inside the explosive at t*=6 for this case.Solidification process takes the longest time for the isothermal top boundary condition.In this case,the solidification is more controlled and enclosed unsolidified region inside the domain does not appear during the process.From this point of view,we can say that maintaining the top surface of the explosive at a higher temperature than the melting temperature decreases the possibility of defect formation. Temperature simulations on Figs.8—10 shows that heat transfer rate is an important parameter for the solidification time.Higher heat loss makes the solidification faster.Lower upper surface temperature on Fig.8 shows that heat loss from top boundary is higher for the convection top boundary condition.Similarly,higher upper surface temperature on Fig.10 give rise to solidification to take longer time for the isothermal top boundary condition. Fig.8 reveals a toroidal liquid region trapped inside the solid explosive for the convection top boundary condition.Combining this information with the fast-cooling process in this set up,it is possible to infer that such toroidal region can be a source of manufacture defects.On the other hand,as it has been shown from Fig.9,the liquid region evolves to a concentrated liquid region near the mold axis for the adiabatic top boundary condition.So,a possible manufacture defect region can appear near the top inlet and around the mold axis.This kind of defect can be prevented introducing a hot probe along the mold axis from the top to the defect region.It is followed by a new cooling process or this hotprobe can be used in the set up during the whole cooling process,preventing the defect formation. Fig.9.Temperature simulations for the adiabatic top boundary condition. The results for the isothermal top boundary condition in Fig.10 show that the solidification front evolves in direction of the top boundary.Then,in this case there is not a liquid region surrounded by solid explosive,but the liquid region at the end of the cooling process is kept at the top of the mold.This is a preferable situation since,combined with the slow cooling process,reduces the possibility of defects formation inside the explosive. Dimensional and dimensionless values of the solidification time for the investigated cases have been presented on Table 3.It has been concluded that,considering defect formation due to the thermal stresses as a result of rapid cooling,solidification process with convection top boundary condition should not be preferred due to the less process time. Table 3Solidification time. Fig.10.Temperature simulations for the isothermal top boundary condition. In this study,a dimensionless model for the solidification under the effect of natural convection inside the explosive has been proposed.This model could also be useful for the parametric analysis of new studies.Thermophysical properties of TNT have been used for the nondimensionalization method in order to satisfy real conditions in the industry. Despite of the relevance of the explosive casting process in antitank shaped charge ammunitions,there are few studies about the solidification process inside a mold with this geometry.Furthermore,the shaped charge geometry effects on the solidification are not negligible,modifying the whole heat transfer process and the fluid dynamics of the liquid explosive. Three different top boundary conditions have been investigated.It has been observed that solidification takes less time for the convection top boundary condition and unsolidified region enclosed by solid phase is observed inside the explosive for the adiabatic and convection top boundary conditions.Solidification takes longer time for the process with isothermal top boundary condition promoting a more homogeneous process preventing the gap formation.Also,an operator can easily control the process from the top and this also prevents the defect formation. The toroidal liquid explosive region observed for the convection top boundary condition case is important to analyze the solidification and the temperature gradient during the manufacturing process.Such hot trapped liquid region promotes thermal stress that can be related to manufacturing defects. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.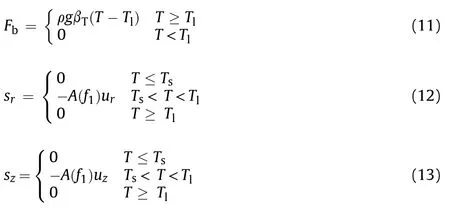
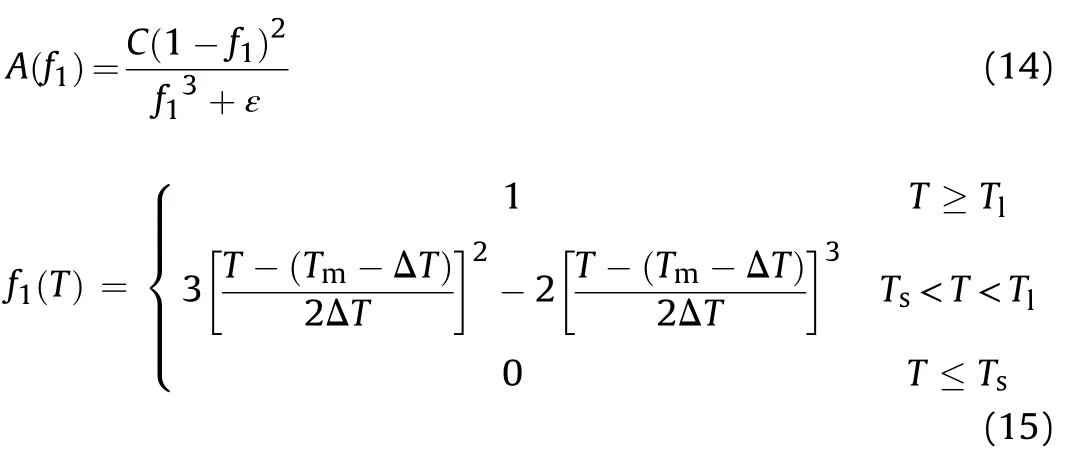
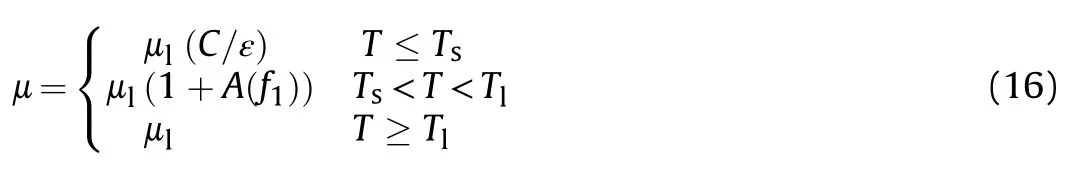



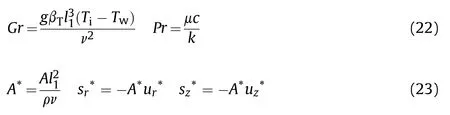
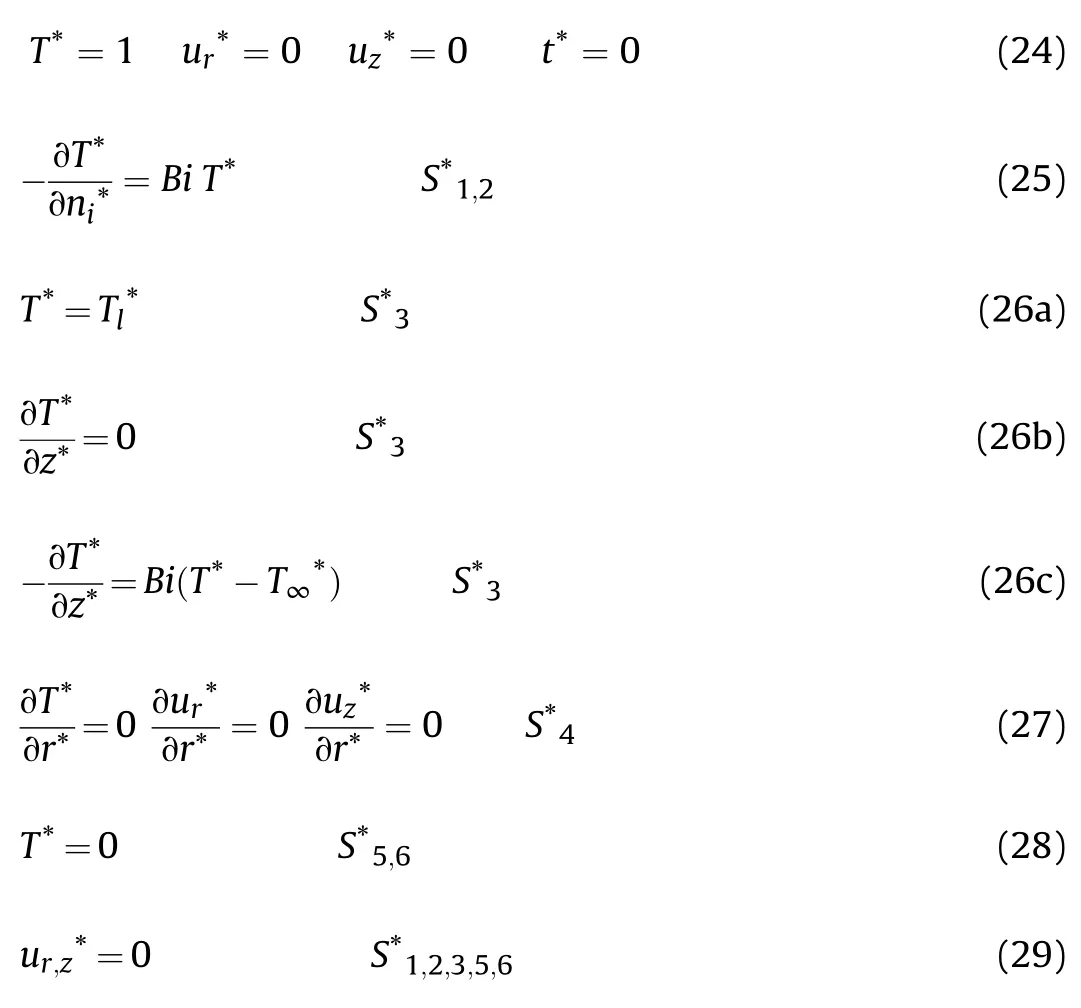

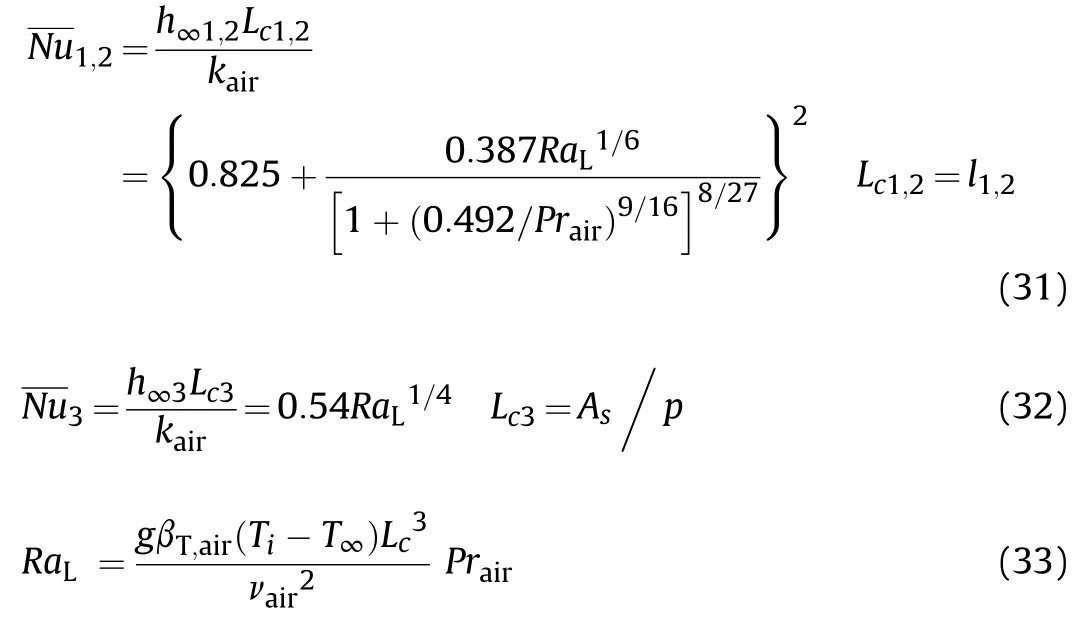
2.1.Verification and validation of the code
2.2.Mesh dependency analysis

3.Results and discussion




4.Conclusion
- Defence Technology的其它文章
- 3D laser scanning strategy based on cascaded deep neural network
- Damage analysis of POZD coated square reinforced concrete slab under contact blast
- Autonomous maneuver decision-making for a UCAV in short-range aerial combat based on an MS-DDQN algorithm
- The properties of Sn—Zn—Al—La fusible alloy for mitigation devices of solid propellant rocket motors
- The surface activation of boron to improve ignition and combustion characteristic
- Numerical investigation on free air blast loads generated from centerinitiated cylindrical charges with varied aspect ratio in arbitrary orientation

