考虑多场景技术和虚拟储能的区域综合能源系统优化调度

上海电力大学电气工程学院 余 蓓 李晓露

1 考虑不确定性因素的场景生成

可再生能源出力及负荷功率具有较强的不确定性，为了确保IES 运行的安全可靠性，在规划和运行阶段考虑风、光等可再生能源及负荷的随机性尤为重要。

本文以历史风、光出力及负荷功率为样本，基于非参数核密度估计法选用高斯核函数生成一天内每个时段的概率密度函数。对随机变量为x 的样本，概率密度函数fh（x）的核密度估计为：

式中：n 为样本容量；Xi为第i 个样本；h 为带宽；K（·）为高斯核函数，即：

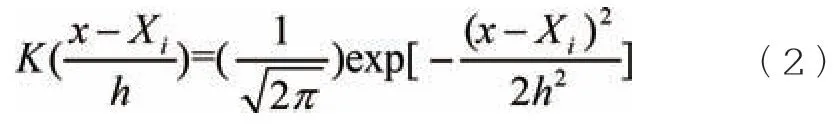
根据风机、光伏出力以及负荷功率每个时段的概率密度函数求出其累积分布函数后，采用拉丁超立方抽样分别对其每个时段的分布函数进行采样，并且为了提高采样场景的准确度，采用Cholesky分解降低不同场景之间的相关性[1]。

2 热网动态模型

典型的热力系统结构如图1所示。热力系统可分为传输系统（一次热网）和分配系统（二次热网），一次热网和二次热网通过换热站实现能量交换。热网中热能的延时和储能特性主要体现在一次热网中，因此本文不计二次热网，仅对一级热网进行讨论。

图1 热力系统基本结构

2.1 热网管道模型

不考虑一次热网中热能损耗，管道i 中的热水从入口到出口所需的时间为τi，有：

式（3）表示不考虑热损耗时，管道i 中热媒在t 时段的出口温度与t-τi时段的入口温度Tini,t-τi相等。其中，li为管道i 长度；ri为其半径；ρ 为水的密度；mi,t为t 时段管道i 中热水流量。

考虑热网中热能损耗的影响，有

一般情况下，hli/cwmi,t的值很小，因此上式可以近似为[2]：

式中：Ta,t为环境温度；Cω为水的比热容；h为传热系数。式（6）描述了热能传输的动态过程。

2.2 一次热网模型

不同管道的热水流入相同节点进行温度混合，即：

式中：Sin和Sout分别为工质流入和流出节点的管道集合。

对于一次热网中的换热站，可将负荷与损耗绑定在一起，看成换热站的计算负荷，本文的换热站模型为：

式中：Hi,t为t 时段换热站i 的换热量；Tspi,t和Trei,t分别为t 时段换热站i 处的供、回水温度。

由于不考虑二次热网，换热站换热量与热负荷之间的关系为：

式中：Qh,i,t为t 时段换热站i 处的计算热负荷。

热网具有延时特性，同一时段流入管道中的热量与流出热量未必相等，因此热网起到了缓冲热能注入与流出的作用，从而表现出类似于储能系统的虚拟充放电特性。当热能供应发生改变导致热量不平衡时，可通过改变一次热网供热量来调节，因此热网就具有了灵活的虚拟热能存储的能力。

3 建筑虚拟储能系统

基于建筑的蓄热特性，根据能量守恒定律可得建筑的热平衡方程[3]：

考虑到影响建筑物内部热量的主要因素，式（10）可表示为：

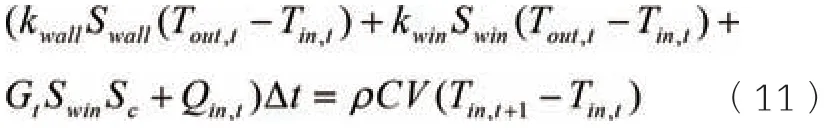
式中：Kwall为外墙的传热系数，Swall为外墙面积；Tout,t和Tin,t分别为t 时段室内和室外温度；Kwin为外窗的传热系数，Swin为外窗面积；Gt为t时太阳辐射强度，Sc为遮阳系数；Qin,t为室内所需热功率。

在建筑物中，由于墙壁和其他结构的隔热作用，室内外的热交换过程缓慢，室内温度不会迅速变化。因此室内温度可以根据温度舒适度要求在一定范围内进行调节，实现类似于储能系统的充放电特性，参与能源系统的优化调度。

因此，同时考虑热网和建筑物的虚拟储能系统充放电方程如下：

式中：Qves,t为虚拟储能系统的充放电功率（放电为正，充电为负）；Qbefore,t为不考虑虚拟储能的热功率需求；Qafter,t考虑虚拟储能时的热功率需求。

4 考虑虚拟储能的IES 优化调度模型

本文的电、热IES 能量供应结构如图2所示。IES 通过风电、光伏、购电，同时调度能源设备的方式为用户提供电、热能供应服务。能源设备主要为热电联产机组（combined heat and power，CHP）和电锅炉，其中CHP 机组以天然气作为输入，进行热能和电力的生产，电锅炉以一部分电能为输入，将电能转化为热能注入热网。

图2 电、热IES 能量供应结构

文中通过日前调度和实时校正两阶段对IES 进行优化调度。日前阶段通过对风电、光伏出力及负荷的不确定性分析，生成多个场景。通过优化设备出力，选择系统运行成本最低的方案作为最优调度计划。校正阶段通过实时修正可控设备的出力，消除预测误差同时，尽可能降低系统的运行成本。

4.1 日前优化调度模型

4.1.1 目标函数

日前，调度以每小时为时间间隔，主要目标是满足区域能源需求和用户舒适度的基础上，将运营成本降至最低。因此，目标函数包括两部分，运行成本和不满足用户舒适性需求而带来的惩罚成本，其中运行成本又包括购能成本和各设备的运行维护成本。

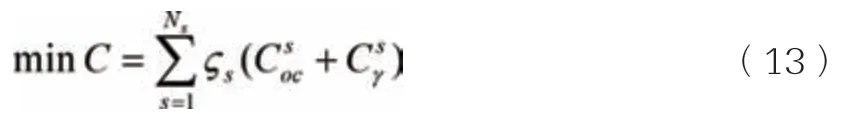
其中，

式中：T 为调度周期；Ns为总场景数；ζs为场景s 发生的概率；Psg,t为场景s 下t 时段购气量，ωg,t为对应的天然气价格；Pses,t为场景s 下t 时段购电功率，ωes,t为对应的电价；αomc为各设备的运行维护成本系数；Psi,t为场景s 下第i 台设备在t时段的出力；γh为用户敏感度系数；Tsin,t为场景s下t 时段室内温度；Tset为室内温度设定值。

4.1.2 约束条件

电功率平衡约束：

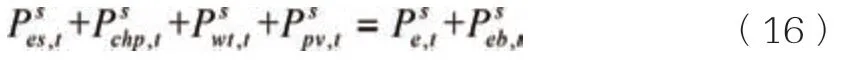
式中：Pschp,t为场景s 下CHP 在t 时段的电功率；Pswt,t、Pspv,t分别为场景s 下光伏、风机在t 时段的电功率；Pseb,t为场景s 下电锅炉在t 时段消耗的电功率；Pse,t为场景s 下t 时段的用电负荷。

热功率平衡约束：

建筑物热平衡约束：

式中：Tin,min、Tin,max分别为建筑物室内温度的上下限。

CHP 机组约束：

式中：kc为CHP 的电热比；ηchp为CHP 效率；Lbg为天然气的燃烧热值。

电锅炉约束：

电锅炉消耗的电功率及相应的热出力满足：

式中：Cop为电锅炉的电热转换系数。

能源设备出力范围约束：

式中：Psi,t为场景s 下第i 个能源设备在t 时段的出力；Pimin和Pimax分别为其出力的上、下限。

4.2 实时校正模型

4.2.1 目标函数

以15min 为周期，实时调整设备出力，降低误差造成的影响，目标函数为：

其中，

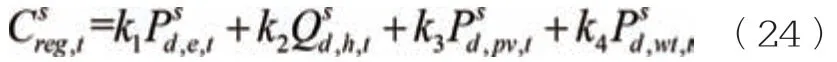
式中：Csreg,t为场景s 下的监管成本；w 为取样时间；Tw为滚动时长；κ1、κ2、κ3、κ4为监管系数；Psd,e,t、Qsd,h,t、Psd,pv,t、Psd,wt,t分别为场景s 下电、热、风机、光伏的预测误差。

4.2.2 约束条件

功率平衡约束：

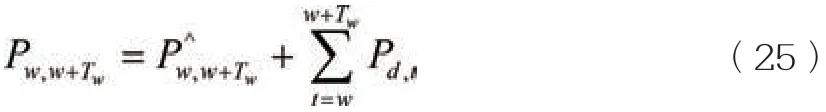
式中：Pw,w+Tw、分别为滚动区间Tw内机组实际和预测出力，Pd,t为t 时段机组误差。

能源设备出力范围约束：

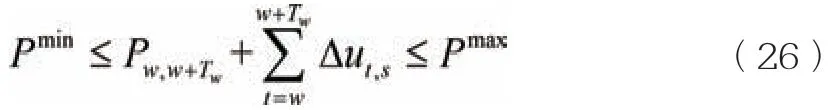
式中：Δut,s为机组相对于采样值的功率变化量；Pmin、Pmax为机组功率上、下限。

5 算例分析

5.1 基础数据

以某园区为例，建立了考虑虚拟储能的IES，考虑一天的经济优化调度。本文中建筑物总容积54000m³，在实际运行功率的基础上，设定光伏、风机的日前预测误差在30%以内，实时校正预测误差在5%内，电、热负荷的日前预测误差在20%内，实时矫正误差在3%以内。利用非参数核密度估计生成每个时段的概率密度函数，通过拉丁超立方采样和同步回代消除法进行场景生成和削减，抽样规模取2000，场景阈值取3，则风机、光伏、电、热负荷分别削减至3个场景，共计34个随机场景，对应的概率为：

式中：Nwt、Npv、Ne、Nh分别为风机、光伏、电、热负荷的场景数；ζwt、ζpv、ζe、ζh分别为对应的概率。

以风机为例，场景生成与削减如图3所示，每个场景出现的概率分别为0.313（红）、0.358（粉）、0.329（黑）。

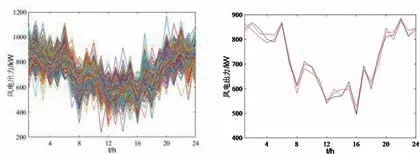
图3 风机样本空间及缩减场景

5.2 运行结果分析

5.2.1 运行流程

考虑多场景技术和虚拟储能的IES 优化调度流程图如图4所示。

图4 优化调度流程图

5.2.2 日前调度优化运行分析

以多场景中的某一场景为例，假设不引入虚拟储能，建筑物内用户设定的温度为22.5℃，优化调度结果如图5所示。

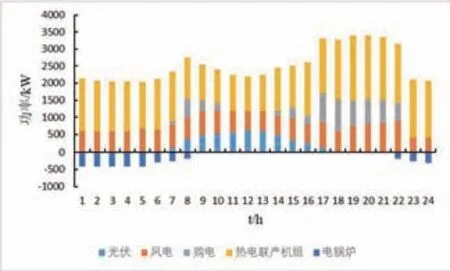
图5 不引入虚拟储能优化调度结果

从图5中可以看出，在不引入虚拟储能的情况下，CHP 机组出力基本随着室外温度的变化而变化。夜间温度较低，风电资源丰富，CHP 机组出力会维持在较高的水平，同时需要电锅炉进行调节，以保证建筑物室内温度维持在用户设定点；在8:00后，随着太阳辐射强度以及室外温度的上升，CHP 机组出力处于较低水平，电锅炉基本不会参与调节。在不引入虚拟储能的情况下，系统的弃风、弃光率为13.89%，总运行成本为23796.36元。

引入虚拟储能，设用户可以接受温度在设定温度的±2℃的范围内波动，用户的敏感度系数设定为0.1，用户设定温度为22.5℃，优化调度结果如图6所示。

图6 引入虚拟储能优化调度结果

由图6可以看出，引入虚拟储能后，由于热网的延时特性以及用户可接受温度的可调性，CHP 机组出力及室内温度有明显不同，出现了较大波动。在23:00～6:00时间段，风电资源丰富且电价较低，适当降低室内温度以减少CHP 机组的出力，从而为风电提供更多的消纳空间。在8:00～11:00以及18:00～22:00时间段，由于天然气价格恒定而电价较高，通过提高CHP 机组出力适当提高室内温度，从而减少该时段购电量，降低了系统的运行成本。相比于不引入虚拟储能的优化调度，系统的弃风、弃光率下降为4.64%，总运行成本下降了5.08%，为22585.21元。从优化结果可以看出，通过热网特性以及在用户舒适度范围内调节室内温度使得虚拟储能系统参与到IES 经济优化调度，可在一定程度上降低系统的运行成本。

图7给出了引入虚拟储能前后，系统虚拟储能优化调度结果。从图中可以看出虚拟储能系统的充放电情况，其中高出基准线的部分为放热，即“放电”，低于基准线的部分为蓄热，即“充电”。一方面由于天然气价格固定，在电价较高的时刻，通过增加CHP 机组的出力可以减少购电量，从而表现为制热需求提升以及虚拟储能充电；另一方面，由于用户可接受温度调节在一定范围内，当制热量到达一定值之后，需要虚拟储能系统进行放电，因此在电价较低的时刻，会适当降低CHP 机组的出力，表现为制热需求降低以及虚拟储能放电，从而为下一时刻虚拟储能充电提供空间。通过这样的调节方式，在满足用户电、热需求的同时，降低了系统的运行成本。

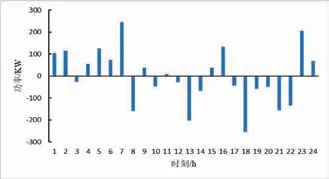
图7 虚拟储能优化调度结果

5.2.3 日内校正运行分析

日前调度阶段，对所生成的每个场景进行优化调度，从而得到系统内可控设备的出力计划，通过分析每个场景出现的概率以及对应的运行成本，选取了综合效益最佳的运行优化方案；实时校正阶段，通过对是否考虑多场景IES 实时校正阶段总调整量进行对比分析，从而体现两阶段优化调度的鲁棒性优势，对比分析结果如图8所示。

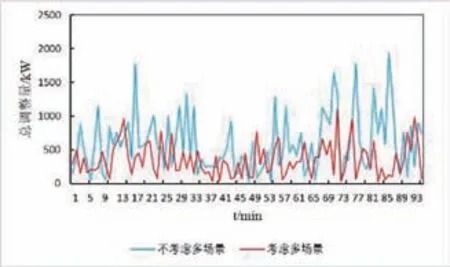
图8 不同模式下实时校正阶段总调整量

通过对是否考虑多场景IES 实时校正阶段调整量进行比较，可以看出考虑多场景的IES 调整总量明显降低。当风、光及负荷功率较小时，调整量相对较低，当风、光及负荷功率较大时，则会出现两种情况，一种是风、光的预测误差修正了负荷的预测误差，使系统的总调整量减少，另一种是风、光的预测误差增大了负荷的预测误差，使系统的总调整量增大。由图8可知，不考虑多场景的IES 误差远大于考虑多场景的IES，特别当风、光的预测误差与负荷的误差成叠加状况时，对比效果更明显。所以，考虑多场景技术和虚拟储能优化调度模型能有效减少实时校正阶段的调度量，从而提高了系统运行的鲁棒性。

5.2.4 经济性分析

本文在基于虚拟储能的基础上，对是否考虑多场景技术时系统的运行成本就行了对比分析，结果见表1。

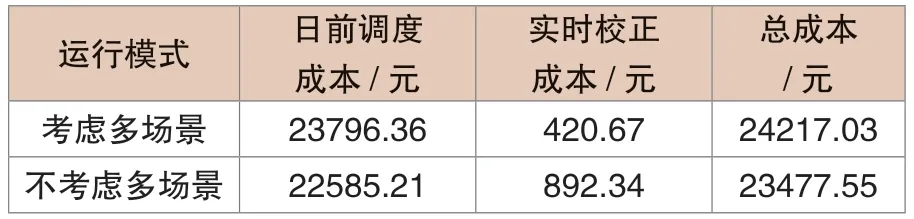
表1 不同模式下系统运行成本

由表1可知，相对于不考虑多场景，考虑多场景时系统的实时校正成本大幅降低，这主要是因为在实时校正阶段考虑了风、光负荷不确定性造成的监管成本后，进一步降低了风、光及负荷的预测误差，减少了实时校正阶段的调整量。虽然考虑多场景时系统的日前调度成本稍高，但是总运行成本明显低于不考虑多场景时系统的总运行成本，说明了风、光及负荷的不确定性确实对系统的优化调度有一定的影响，从而验证了模型的经济性和必要性。