多品种小批量生产模式下共轭贝叶斯动态质量控制方法
李晓波,孙小慧
(新疆大学 建筑工程学院,乌鲁木齐 830017)
对于制造业而言,产品质量是企业重要关注的议题之一,也是影响企业利润率的重要因素。通过对生产各个阶段进行过程控制可以发现制造过程中存在的异常情况并进行分析,给出相应的解决办法和措施,完成质量控制和提升。
随着全球经济的快速发展,市场经济的需要也在不断地变化,多品种、小批量的生产模式也在逐步演化成现在最主要的生产模式。目前,多品种、小批量生产方式下工序质量控制主要有4种方法:精确控制界限法、成组技术法、统计变换法和贝叶斯估计法。
20世纪50年代King[1]第一次提出精确控制界限法,此法以小样本数据量为基础设置精确控制界限,控制限下的每个质量数组误报错误的概率持续在较小的值。该方法局限于控制图中的控制限随着样本容量的调整而变化,对样本容量的变化很敏锐,容易忽视漏发报警。为了解决精确控制界限法漏发报警的缺陷,国内外学者以成组技术中的相似性理论为依据,通过充实样本容量解决过程质量控制中数据量较少的问题[2]。Desmond[3]针对多品种、小批量数据缺少问题,提出工序质量控制一个工序中其他相似零件可以提供质量信息的想法从而扩充质量数据库,为实现精确质量控制提供关键理论方法。杨旭等[4]对成组技术中的相似工序法进行研究,认为生产过程中各工序之间是相似的,同时影响工序质量的各因素也是相似的并存在密切相关性,同时给出了计算相似度的方法。
成组技术虽然解决了质量控制中数据量较少的问题,但不同产品、不同批次的质量数据相关性和不是同一分布的问题,给数据分析工作带来阻碍。为了满足不同产品独立同一分布,同时也为了消除不同生产过程中不同均值和不同公差带来的不利影响,国外学者Quesenberry[5]提出通过统计变换解决过程质量控制中数据统计问题,该方法为了实现不同母体数据采用相同统计方法处理,引入标准正态数据变换将数据正态化来完成。余忠华等[6]将成组技术中相似元理论与统计变换过程控制方法相结合,提出了通过相似元分析和统计变换来构建相似工序,实现生产过程中质量的有效控制,该方法局限于需要相关产品技术支持,且收集的数据一般可能为非正态分布。
当统计的生产过程质量数据服从非正态分布时,国内外学者提出了以贝叶斯估计为基础的统计控制方法,该方法将生产过程中的历史数据与人们的主观评价、预测和判断相结合,通过控制图和过程能力分析建立实时跟踪与预警的生产质量控制模型,从而在低样本容量下实现高精度预测。卡祥民等[7]以贝叶斯分析为理论基础,将先验和样本信息相结合用贝叶斯理论估计当前产品质量数据的分布参数及回归系数,并根据所得参数绘制相关控制图,实现对小批量生产的质量管理。该方法在生产过程变动不大的产品过程质量控制中得以应用,当此方法遇到生产过程变化大时,如生产品种较多,批量小,加工工序复杂,会因无法获得足够多历史样本数据而无法使用。赵飞涛[8]对多品种、小批量生产模式进行研究,提出通过共轭贝叶斯估计完成统计过程控制模型的建模,在当前少量容量下有效地估计2个或2个以上未知参数,有效规避以往贝叶斯估计在估计2个或2个以上未知参数的局限性。但该方法未考虑先验信息中历史批次质量数据的加工时间与当前批次的加工时间的相关关系,即先验信息中历史批次质量数据的加工时间与当前批次质量数据的加工时间越靠近越能反映当前的生产状况,如不考虑此种情况会引起统计过程控制活动的无效或引起严重的质量问题,所以在研究中各先验信息权重占比需考虑进去。
针对多品种、小批次生产模式国内外研究的局限性,本文引入共轭贝叶斯理论,实现及时追踪和反馈的工序质量控制目的。首先根据成组技术中的相似理论选择备选先验信息,通过统计变换方法将历史数据进行变换处理,经过里尔福斯(Lilliefors)检验、联合假设检验(F检验)确定为先验信息;然后以时间序列指数加权理论对历史数据各批次赋予权重;其次通过共轭贝叶斯方法完成工序质量控制模型的建立,在产品质量数据累计过程中计算控制限,实现工序质量控制的及时追踪与预警;最后通过实际案例利用MATLAB工具比较此种方法与常规方法的优缺点。上文提出的共轭贝叶斯统计控制方法流程如图1所示。

图1 共轭贝叶斯工序质量控制方法流程图
1 先验信息的确定
产品工序质量控制的第一步就是收集一段时间段内与相似理论相符的历史质量特征数据,然后以数据变换的方式将各批次相关数据转换为具有同分布的情况,其次对变换后的历史质量数据做方差和均值的齐性检验,最后将检验合格的历史质量数据作为共轭贝叶斯建模的先验信息。
1.1 成组技术
运用成组技术,首先就是要利用工序相似性分类方法对工序相似性研判。企业根据现场实际情况选取相应方法,如目测分类法等,将生产中的影响工序质量的5M1E,即人、机器、材料、方法、环境和测量5个因素,通过筛选、分类汇总,构建工序相似性评定模型,通过以上模型收集相关重要工序同组内的历史批次质量数据,将其作为备选先验信息。
1.2 数据变换
由于各部件的基本尺寸和公差值的差异,导致了其历史批次质量数据平均值μ和方差δ的差异,因此,必须对不同零件的历史批次质量数据进行规范化,实现相似工序质量特征数据的同一分布。数据处理流程如下

式中:yij为标准化数据;xij为j批样本中的第i个样本实测数据;Mj为第j批样本的公差中心;Tj为第j批样本的公差,Tj=TUj-TL。

式中:TUj为第j批数据的上偏差;TLj为第j批数据的下偏差。
1.3 先验信息筛选
用Lilliefors检验对待选的m批先验样本信息进行筛选[9],方法如下。从m批样本中随机抽取第j批样本xj进行检验,原假设为xj服从正态分布,Lilliefors检验的检验统计量为

式中:sup为集合中的最大值;G(yj)为第j批样本累计分布函数;F(yj)为以第j批样本均值和方差为总体均值和方差的累计分布函数。样本均值和方差依据式(4)执行。
当D检验统计量小于等于标准值时,原假设成立,即该样本特征服从正态分布。

为了保证备选数据与当前样本数据方差的一致性,需先利用Bartlett's球状检验[10]进行判别,Bartlett's球状检验的原假设H0为所有的样本总体即m+1批数据的方差σj2是否相等。样本容量为nj的(m+1)批样本中,用第m+1批样本方差Sj2代替第j批样本的总体方差σj2估计值,Bartlett's球状检验统计量为
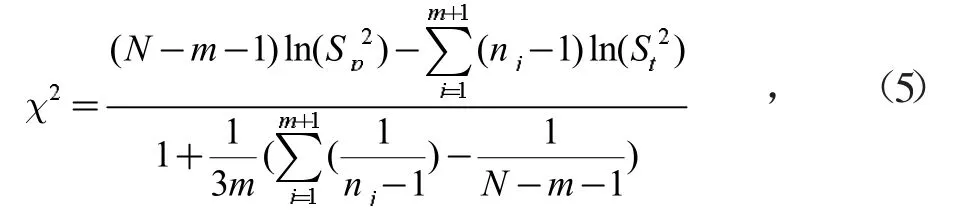
为了保证备选数据与当前样本数据均值的一致性,确保共轭贝叶斯估计中先验和后验分布总体均值一致。需采用单因素方差分析确定备选数据与当前样本均值是否相同。即采用F检验
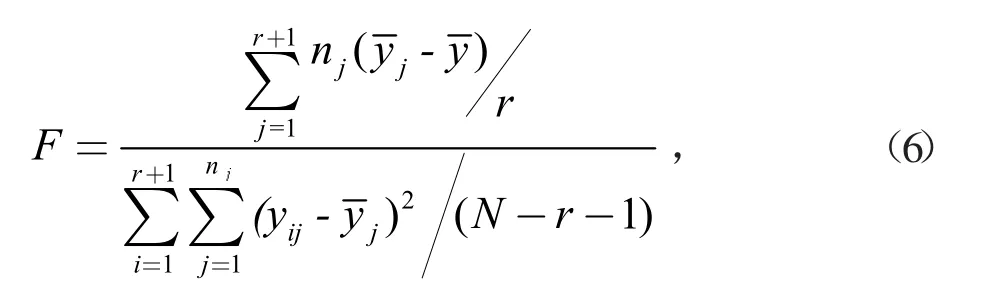
当F>Fa(r,N-r-1)时,备选信息中各批次样本组的总体均值不同,且Fa(r,N-r-1)为F的临界值不能作为先验信息,还需对剩余备选信息中的样本组重新进行F检验,直至出现F<Fa(r,N-r-1),最终得到m批的历史数据,将其做为可选的先验数据。
2 共轭贝叶斯质量控制模型建立
2.1 控制图的建立
产品的好坏有一定的随机性,产品质量特征值可以反映质量的好坏程度,把这种随机性分布通过建立产品质量控制模型进行监控,一般认为质量控制模型建立在正态分布连续随机变量的基础上,而产品的质量特征值落入(μ-3σ,μ+3σ)的概率为99.7%。由此确定产品特征值的控制图:CL为中限,UCL为上控制限,LCL为下控制限。

由公式(7)可知,质量控制的效果主要取决于对质量数据均值μ和方差σ的准确估计,利用共轭贝叶斯控制模型可以充分利用先验信息提高参数μ、σ估计准确率,从而实现对质量的有效控制。
2.2 共轭贝叶斯参数的估计
2.2.1 先验信息均值、方差计算及权重分配
通过数据变换、筛选后历史数据得到(y1,y2,y3,y4,…,ym)=Y组先验数据,且服从正态分布N(μ,σ2),则各历史数据为yij=N(μj,σj2)。

式中:nj为第j批历史数据样本容量n。
企业在生产过程中,加工时间与当前生产批次靠近的历史数据,应该与当前生产情况有更紧密的联系。由此可以根据时间序列中的指数加权思想为各批次历史数据进行赋权值。
根据多品种、小批量生产模式自身特点,因企业检验方式的不同,可能造成各批次所选取的历史数据的数量也有可能不同,为此可通过变样本容量计算公式获得各历史数据间的均值和方差。
将指数加权思想和多品种、小批量生产模式下变样本容量计算公式相结合,可得历史的质量数据的组间均值和方差为

2.2.2 μ,σ2参数估计
根据贝叶斯理论中多参数模型,若先验信息已知,总体方差σ2未知,总体方差服从逆伽马分布(IGa),即σ2的先验分布为逆伽马分布,记为IGa(α,β),μ的先验分布为正态分布,考虑到μ和σ2间有相互影响,故其共轭先验分布有乘积形式π(μ|σ2)π(σ2),可以表示为μ|σ2~N(a,b2);σ2~IGa(α,β)。μ,σ2分布参数依据先验数据计算可得,计算方法如下。
(1)σ2的估计,因σ2~IGa(α,β),根据逆伽马分布的性质,可得
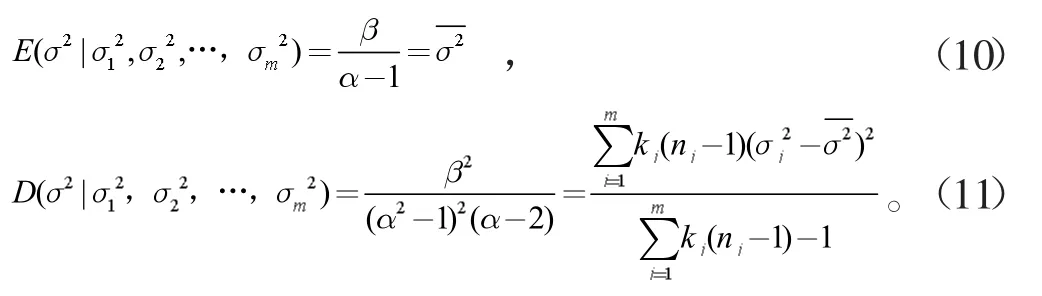
联合(10)和(11)可得

在获得当前数据Y后,当目前样本σ2服从逆伽马分布,由共轭贝叶斯理论可知,其后验与先验分布形式相同,可记作
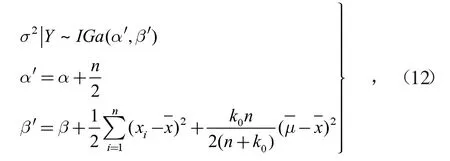
由此可得σ2的贝叶斯估计

(2)μ的估计,因μ|σ2~N(a,b2),根据正态分布性质可得μ期望值

在获得当前批次样本数据Y后,由共轭分布性质可得

因联合先验分布为π(μ,σ2)=π(μ|σ2)π(σ2),由此可得,联合后验分布π(μ,σ2|Y)可得条件后验密度π(μ|σ2,Y)和边缘后验密度π(μ|Y)的乘积,将联合后 验密度σ2积分,可得μ的边缘后验密度

利用逆伽马分布密度函数的正则性性质,得出
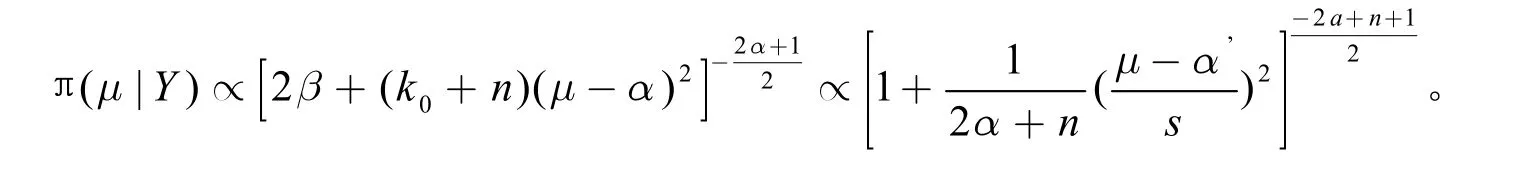
这是个自由度为(2α+n)的t分布,其中

由此可得μ的贝叶斯估计为

(3)计算控制限。依据多品种、小批量生产模式下质量数据的特点,选用单值-移动极差控制图,同时结合生产过程中实际数据,根据式(13)、式(14)计算α,β贝叶斯估计值,求控制图控制限
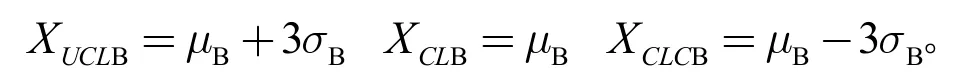
移动极差控制限为

依据统计学的原理,得移动极差控制限计算公式可以转化为

2.2.3 工序过程能力
在生产中,工序能力是否满足要求计算公式如下

式中:CP为工序能力指数表示过程均值与公差中心值重合时的状态;CPK为工序能力指数过程均值与公差中心值有偏移的状态;μl,σl分别为未变换前的原始数据的均值和标准差。
3 实例验证
以某电机制造厂家总装车间中的转子导条涨紧工序为例,利用MATLAB仿真比较本文方法与现有常用最大似然估计方法的优劣。

表1 历史质量特征数据
假设工序过程能力指数为1.67并进行仿真,由此可得,每批数据的标准差σij=Tj/6,均值为Mj。根据式(16)可得,总体分布的均值μ=0,标准差σ=σij,Tj=1/10,由此可根据正态分布(0,0.01)生成仿真数据。
本文采用的单值-移动极差控制图的效果主要取决于对分布参数总体均值μ和总体方差σ的准确估计,故本文通过MATLAB生成数据与历史数据相结合,比较本文方法与最大似然估计在总体均值μ和总体方差σ的估计情况,已确认本文方法的有效性。
具体仿真过程如下。
(1)根据正态分布(0,1/10)生成数据,然后从中取n个数据作为当前批次,n的初始值为1,计算当前样本的均值μ和方差σ2。
(2)根据表1,从其中抽取10批数据,每批历史数据确定为30个样本。抽取的样本数据经过式(1)变换后,先后进行Lilliefors、Bartlett's球状、方差分析(ANOVA)检验确定选定的历史数据与当前的数据是否来自同一分布,如是留存,不是弃之,直至生成样本容量为30的10组历史数据。
(3)将指数加权思想与各批次历史数据进行指数加权结合,可得历史数据的组间均值和方差。
(4)利用先验历史数据计算超参数μˉ,σˉ,α,β。
(5)利用当前数据信息结合超级参数通过贝叶斯模型得到贝叶斯参数估计的值。
(6)以传统的方法最大似然估计得出当前样本的参数值。
(7)计算样本容量m下的平均绝对误差

式中:xmn为仿真估计值;Ln为样本容量n下真实值。
由图1、图2可知,当目前样本量持续增大时,最大似然和共轭贝叶斯计算所得的分布参数估计的平均绝对误差逐渐降低,但是当选择样本数量时以共轭贝叶斯估计为基础的平均绝对误差比最大似然估计要小得多。绝对误差能够反映估算值的准确度,而随着误差的持续变化,估算值的持续缩小和真实状况也随之接近。由此得出2个结果:一是在小样本生产条件下,共轭贝叶斯估计更能反映实际情况;二是随着样本的增加,估算值的接近程度也随之提高。

图1 总体均值下2种估计方法的平均绝对误差比较
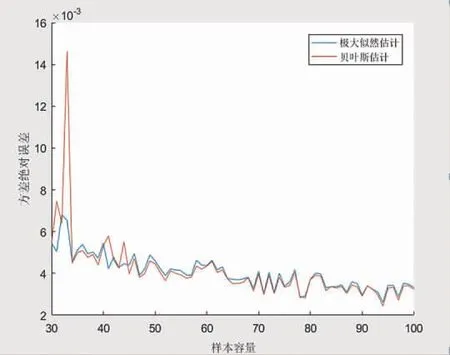
图2 总体方差下2种估计方法的方差绝对误差比较
本文结合成组技术中相似理论同时利用数据变换方法,通过数据检验,将各批次历史质量数据作为当前数据的有效补充,同时通过指数加权将各批次数赋予权重。利用共轭贝叶斯理论的优点,实现产品质量的及时追踪和反馈。为了验证本方法的有效性,本文通过仿真与现有传统方法比较,本方法在适用范围、控制效果等方面均有显著效果,在多品种、小批量工序质量控制中能有效解决质量控制问题。因在生产过程中的观测值呈现出自相关性,为此在后期工作中,需进一步对研究观测数据相关性进行分析,实现此模型下多品种、小批量工序质量控制的有效性。

