方程思想在数学建模中的应用
甘肃省秦安县第二中学
王永强
数学是研究现实世界数量关系和空间形式的科学.人类历史发展中数学是最先且一直应用在实际生活中的一门科学.任何一个科学领域都离不开数学,数学是一切科学的基础,也是一切科学的灵魂.数学的特点不仅在于概念的抽象性、逻辑的严密性,而且在于应用的广泛性.我们只有掌握了数学的广泛的应用,并能用数学知识解决各种各样的实际问题,才能说真正学会了数学.数学建模是应用数学知识解决实际问题的重要手段和途径之一,它可以促进学生解决实际问题的能力,引导学生应用数学知识的意识,培养学生学习数学的兴趣.数学知识的应用主要和数学建模的方法结合起来,利用数学建模来解决生活中的实际问题.
其中方程思想往往通过和函数思想、不等式思想、数形结合思想等的结合,可以解决现实生活和生产过程中的很多问题.本文中选取经济活动、数据测量、军事国防等方面的具体实例,寻求解决这些问题的办法.
1 在经济活动方面的应用
现实生活中,我们会遇到向银行存款时怎样存款获得的利息最多,按揭贷款买房时怎么贷款支付的利息最少等合理使用资金的问题.这些问题可以应用方程思想来解决,下面我们举一个银行存款的问题.
1.1 问题提出
北京大学学校基金会有一笔M万元的基金,打算将其存入银行或购买国库券,当前银行存款及各期国库券的利息见表1.假设国库券每年至少发行一次,发行时间不定,取款政策参考银行的现行政策.
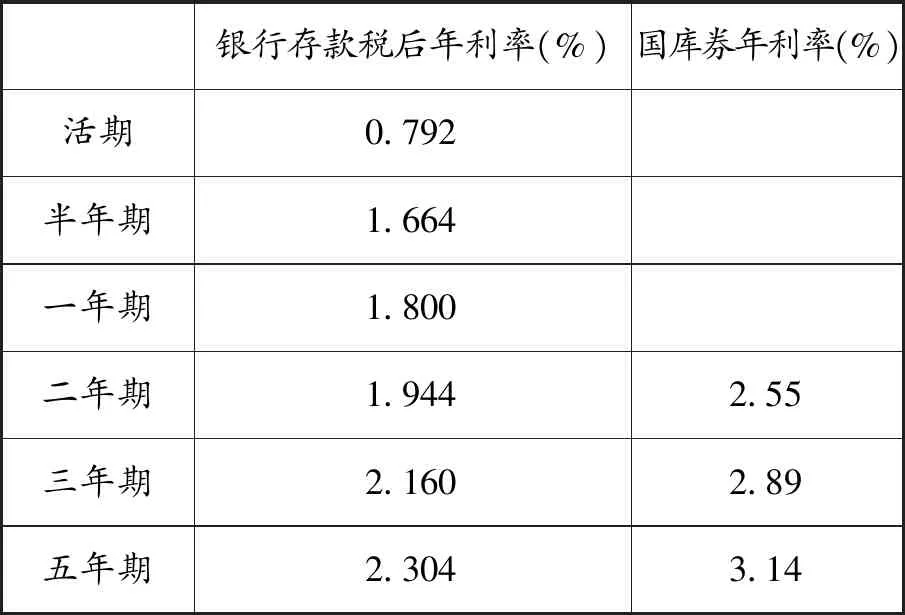
表1 银行存款、国库券年利率表
北京大学学校基金会计划在每年用部分本息资金奖励优秀的师生,要求每年发放的奖金额大致相同,并且让基金使用N年后M万元的基金不能减少.
请你帮助北京大学学校基金会在如下情况下设计基金使用方案.
假设M=5 000万元,N=10年.北京大学在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其他年度多20%.请给出具体分析结果.
1.2 模型假设
(1)假设银行利率和国库券利率一直保持不变.
(2)假设每年存取款也就是国库券发行期.
(3)假设每年奖金发放时间不定,和存取款时间相同.
1.3 模型分析
本模型的一个目的是提高所得利率,从利率表可以看出银行存款或国库券时间越长,利率越大,收益越大.另一个目的是每年利用大致相同的部分本息资金奖励优秀师生,也就是每年要取出一部分钱来使用.满足这两点,模型才合理.通过对利率表的分析,时间越长,利息越多.如果在同一年期国库券利率高时就买国库券,银行利率高时就把钱存入银行,也就是把钱存在同期利率高的方式做投资.
我们假设:
X1表示1年期存款数,一年后连本带利发放奖金;X2表示购2年期国库券数,二年后连本带利发放奖金;X3表示购3年期国库券数,三年后连本带利发放奖金;X4表示购2年期国库券数,到期后连本带利再购2年期国库,四年后连本带利发放奖金;X5表示购5年期国库券数,五年后连本带利发放奖金;X6表示购3年期国库券数,到期后连本带利再购3年期国库券,六年后连本带利发放奖金;X7表示购5年期国库券数,到期后连本带利再购2年期国库券,七年后连本带利发放奖金;X8表示购5年期国库券数,到期后连本带利再购3年期国库券,八年后连本带利发放奖金;X9表示购5年期国库券数,到期后连本带利再购3年期国库券,再到期后连本带利存一年定期,(也可以购5年期国库券,到期后连本带利再购2年期国库券,到期后连本带利再购2年期国库券,但这种方案没有前者优),九年后连本带利发放奖金;X10表示购5年期国库券数,到期后连本带利再购5年期国库券,十年后取出,发放同等的奖金,剩余部分还是原来的基金.
X1+X2+X3+X4+X5+X6+X7+X8+X9+X10=5 000.
①
X1(1+0.018)=X2(1+2×0.025 5)
=X4(1+2×0.025 5)2
=X5(1+5×0.031 4)
=X6(1+3×0.028 9)2
=X7(1+5×0.031 4)(1+2×0.025 5)
=X8(1+5×0.031 4)(1+3×0.028 9)
=X9(1+5×0.031 4)(1+3×0.028 9)(1+0.018)
=X10(1+5×0.031 4)2- 5 000
②
可以把方程组②的数据依次利用换元法变成X1的代数式再代入①式,这样就把①式变成只含有X1的一元方程来解题,就可以求出每年的基金使用计划.限于本文主要探究数学的方程思想在数学建模中的应用,具体解题过程在此不再详述.
2 在数据测量方面的应用
方程思想可以简单快速解决许多问题,如在安装中央空调时、架构高压线时电阻的测量等就可以利用方程的思想来解决.以下我们举一个关于中央空调电阻的测量问题.
2.1 问题提出
有一幢100层大厦安装了中央空调,装成之后发现仪表显示的温度和实际温度有较大的误差.经过分析发现由于连接仪表的三根导线电阻不相等所致,只有测出每根导线的电阻才可以解决仪表不准的问题.每根导线都从一楼连接到顶楼,很明显直接测量每根导线电阻是不可能的,因为导线一头在一层,另一头在一百层.那么应该怎么办?
2.2 模型假设
我们应用数学的方程思想,假设:三根导线的电阻分别是Ra,Rb,Rc.把导线a和b,b和c,c和a在楼房顶部连成一个回路,在一楼就可以使用电阻表分别测量.
2.3 模型分析
我们依次利用连接的三个电路,再使用电阻表在楼房底部分别测出每一个回路的电阻,假设测定的电阻分别为X,Y,Z,那么就有方程组
Ra+Rb=X
③
Rb+Rc=Y
十九年,似乎一切全变了,又似乎都没有改变。死了许多人,毁了许多家,许多可爱的生命葬入黄土。接着又有许多新的人继续扮演不必要的悲剧。浪费,浪费,还是那许多不必要的浪费——生命,精力,感情,财富,甚至欢笑和眼泪。我去的时候是这样,回来时看见的还是一样的情形。关在这个小圈子里,我禁不住几次问我自己:难道这十八年全是白费的?难道在这许多年中间所改变的就只是装束和名词?我痛苦地搓自己的手,不敢给一个回答。
④
Rc+Ra=Z
⑤
联立方程组③④⑤可以算出每根导线的电阻Ra,Rb,Rc.
再根据物理知识给三根导线分别串联合适的电阻就可以使三根导线的电阻相等了.
3 在军事国防方面的应用
测量大海上驶来的一艘军舰的长度大小和位置方向,空中飞来的敌机的高度和位置,敌国导弹发射基地的位置,测量河流的宽度,楼房的高度,山的高度,等等,我们也可以尝试利用数学的方程思想和数形结合思想去解决这类问题.下面我们举例一个测量高度的问题.
3.1 问题的提出
大家都看过电影《攀登者》吧?为了登上珠穆朗玛峰的山顶测量海拔高度,花费了巨大的人力物力,甚至有人为此付出了生命的代价.如果我们不用登上珠穆朗玛峰的山顶,能否可以测量出它的海拔高度呢?
3.2 模型的假设
如图1,只要测量人员在珠穆朗玛峰的山脚下D点可以测量出D点的海拔高度,那么珠穆朗玛峰山顶A点的海拔高度也就可以解决了.

图1
3.3 模型的分析
首先在Rt△ABD中,测出测量人员从点D观察珠穆朗玛峰最高点A的仰角,即∠ADB的大小,如果再计算出AD的长度,就可以计算出H=ADsin∠ADB.
为了计算AD的长度,需要确定一个与点D在同一水平面的观察点C,首先测量出CD的长度,再使用仪器测量出∠ACD和∠ADC的大小,就可以计算出∠CAD=π-(∠ACD+∠ADC),最后利用正弦定理,得

把上面结果代入H=ADsin∠ADB就可以计算出高度H.
因此,可以计算出珠穆朗玛峰的海拔高度=D点的海拔高度+高度H.
通过上面的一些具体实际生活问题的探究,我们可以看出数学知识在实际生活中的应用较多,且非常科学、严谨.其中方程思想在数学建模中的应用更是非常广泛和巧妙.因此,我们必须要学好数学、用好数学,更要应用数学知识去解决实际生活中的一些问题.

