人口规模、交易成本和城乡空间经济
——基于新经济地理学城市体系模型的理论研究
何 文
(上海理工大学 管理学院,上海 200093)
目前,我国形成了以京津冀、长三角和珠三角等城市群为核心的空间经济版图。以人口规模作为实力的重要表征,城市群之间进行着事实上的人口“竞赛”。要扩张城市人口规模,在短期内只有两条路径:一是城市化,即吸纳农村人口;另一条是从其他城市“争夺”人口。城市群内部的重要城市之间乃至城市内部的不同经济区之间,均在进行着对于人口的“追逐”。为此,除了北京等少数城市外,各地均不断放松落户限制。户籍制度的改革持续改变着我国的城乡空间经济格局[1-2]。
长期以来,我国不仅有着严格的户籍制度,而且长期执行计划生育政策。严格的人口控制政策曾被认为有力地维护了我国的经济发展[3-5]。近年来,计划生育政策日益松动,各地逐渐放开二胎,一些地区甚至推出了鼓励生育的政策。人口政策的调整反映了人口在经济发展中的角色属性发生了变化——在限制生育时期,人口更多地呈现为经济发展的负担;而在鼓励生育时期,人口对于经济发展的资源属性则更明显[6]。各地区近年来竞相争夺人口,一些城市甚至出台了鼓励在当地落户的人口(人才)吸引政策。这表明,地方政府意识到人口的资源属性对于当地经济发展的重要意义。
探究人口政策转变的动力,思考人口对于城市发展的意义,是本文研究的出发点。一些研究用实证方法评估了计划生育政策调整对于我国经济发展的影响[7-10]。本文则尝试构建理论模型,探究在城市竞争关系中人口流动的微观机理,分析人口总量的变化对各城市和城乡空间经济所带来的影响。
以一般均衡框架和空间分析等为特征,新经济地理学(NEG)能够较好地展示要素流动的微观机理。特别是,相比于NEG的核心—边缘系列模型所采用的抽象空间、虚拟区位以及通常要求部分劳动力无法跨地区自由流动的设定,NEG城市体系模型[11-14]构建于真实的连续经济空间和实体化的城乡区位,且所有劳动力都能够跨区域流动,为本文的研究提供了良好的分析框架。因此,本文将发展NEG城市体系模型,构建一个包含双城市、具有城乡结构的理论模型,探讨在交易成本变动背景下,人口规模变动对城乡空间经济的影响。
一、理论框架
如图1所示,假设经济空间为线性连续结构,由两个同质城市和农村三部分构成。不考虑城市内部的空间结构,即设城市为一个点;以两个城市的中点为原点(坐标为0)建立坐标轴,分别设定两个城市为城市1和城市-1,两个城市分别位于r1和r-1点,r-1=-r1。由于两个城市为同质城市,因此经济区的范围也必然是对称的,设为由f到-f,f和-f表示为经济区的两个边界,基于对称性,我们只需要考虑r≥0的部分。

图1 双城市的城乡空间经济结构
不考虑失业问题,假设经济系统中只投入劳动力和土地(耕地)两种生产要素从事农业和工业两种产业。农村为农业区,投入土地和劳动力采取里昂惕夫生产技术生产同质的农产品在完全竞争市场上销售;每1单位土地投入aA单位劳动力,产出1单位农产品。城市是工业区,工业部门投入劳动力,采用规模报酬递增技术生产具有差别化的工业品在垄断竞争市场上销售。工业品由城市销往农村,农产品由农村销往城市,两者均存在交易成本。
设经济系统的总人口和单个城市人口分别为L和LM,农民总数为2aAf;这样就有:
L/2=LM+aAf
(1)
式(1)可以称为人口(劳动力)条件。
(一)消费者行为
假定所有消费者具有相同的偏好。采用经典的D-S框架,设定消费者效用函数为双层效用函数——消费农产品和工业品的C-D型总效用函数以及消费工业品组合的CES效用函数。用μ和1-μ分别表示消费者对于工业品和农产品的消费偏好程度,这里μ∈(0,1);σ表示任意两种工业品之间的替代弹性,这里σ>1,σ越大表示工业品的差别化程度越小;n为所有工业品的种类数。
1.城市和工人
城市居民(即工人)的效用函数为:
UM=μlnCM+(1-μ)lnCA,
(2)
这里,UM为城市居民的效用;CM为城市居民消费的工业品组合;CA表示城市居民对农产品的消费;ci表示城市居民对第i种工业品的消费量。分别用wM和VM表示工业劳动力的名义收入水平和实际福利水平,分别用PA(r)、pi(r)和PM(r)表示r地区的农产品、第i种工业品和工业品组合的价格。工人消费行为的预算约束可以表示为:
PA(r1)CA+PM(r1)CM=wM,
(3)
结合式(2)和(3)可以得到城市居民的实际福利水平(间接效用函数)
VM=lnwM-lnP(r1)=lnwM-μlnPM(r1)-
(1-μ)lnPA(r1)
(4)
这里,P(r)=[PM(r)]μ[PA(r)]1-μ表示r地区的(所有产品综合的)物价水平。
2.农村和农民
在城市和工人的对应变量后面加上(r),以表示r地区的农村或农民的变量。农村居民(农民)的效用函数为:
U(r)=μln[CM(r)]+(1-μ)ln[CA(r)],
(5)
这里,U(r)为r地区农民的效用;CM(r)为r地区农民消费的工业品组合;CA(r)表示r地区农民对农产品的消费量;ci(r)表示r地区农民对第i种工业品的消费量。
分别用w(r)和V(r)表示农民的名义收入水平和实际福利水平。r地区农民消费行为的预算约束可以表示为:
PA(r)CA(r)+PM(r)CM(r)=w(r),
(6)
结合式(5)和(6)可以得到农村居民的实际福利水平:
V(r)=lnw(r)-lnP(r)=lnw(r)-μlnPM(r)-
(1-μ)lnPA(r)
(7)
(二)交易成本
工业品和农产品在城乡之间销售均有交易成本,模型采用冰山交易成本,用τ表示单位距离产品的损耗比例,τ≥0。这意味着,出售一单位产品到距离r单位远的地区,只剩下e-τr单位,1-e-τr单位都在运输过程中“融化”了①。可以得到:
p1(r)=eτ|r-r1|p(r1),p-1(r)=eτ|r+r1|p(r1),
PA(r)=e-τ|r-r1|PA(r1)②
(8)
这里,p1(r)和p-1(r)分别表示两个城市的工业品在r地区的价格水平。
(三)农业部门和土地租金
用R(r)表示r地区的土地租金,等于每单位土地的产值减去耕种土地所需要的aA单位劳动力的总工资:
R(r)=PA(r)-aAw(r)
(9)
这里,aA代表农业生产技术,数值越小则表示单位产出所投入的劳动力越少,也就意味着农业技术水平越高。在经济空间边界(f地区)的土地租金为0:
R(f)=0
(10)
(四)工业部门
工业部门为D-S垄断竞争的市场结构,假定不存在企业之间的共谋以及范围经济,由于具有规模报酬递增技术,故而一种产品只由一个企业生产。假定每个企业使用F单位劳动力作为固定投入;每单位产出需要aM单位的劳动力作为可变投入。这样,企业的成本函数为wM(F+aMxi),这里x表示企业的产出。因此,企业的利润为:∏=px-wM(F+aMx)。假设产品数量充分多,选择恰当的劳动力计量单位,令aM=1-1/σ,F=1/σ,可以得到企业的最优定价为:
p=wM
(11)
以城市劳动力工资作为计价物标准,即令wM≡1,这样,本文中所有的价格指标(如名义工资和物价等)都可以理解为该指标与城市劳动力工资的比值。垄断竞争的市场结构下企业进出市场无限制,因此超额利润为零。由此可以得到企业的产量和每个企业使用劳动力数量均为1,以及一个城市的工业品种类数:
n=LM
(12)
由于所有企业同质,从而可以得到工业品价格指数:
(13)
(五)市场出清
模型中不存在储蓄和税收,从而整个经济系统的总收入即总支出。总支出包括消费者在农产品和工业品两方面的支出。工业品总支出既是工业部门的总收入,也是所有居民支出的μ份额:
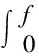
(14)
由于只有农产品和工业品两个跨区域市场,因此工业产品市场出清意味着农产品市场也出清了。
二、均衡分析
当居民能够自由流动时,经济系统实现均衡的条件为所有居民的实际福利水平相等:
V(r)=VM
(15)
根据人口条件、市场出清条件和福利均等条件,可以得到模型的均衡。由于无法得到模型的解析解,本节主要采用图解法,选取适当的参数③,通过数值模拟来展示结论;并通过不同参数下结论的比较来展示结论的稳健性。在无法完全通过图解法展示结论之处,结合微分分析进行判断。
(一)城市人口
图2中,横轴和纵轴分别表示(经济系统的)人口总量L和单个城市的人口LM。随着人口总量的扩大,城市人口也随之增加。工业品的交易成本是推动人口向城市集聚的动力之一,而农产品的交易成本则是导致人口向农村分散的动力之一。给定人口总量,交易成本对于城市人口的影响取决于两者效果的权衡。对均衡条件进行微分分析,可以得到:

图2 人口规模与单个城市的人口④(模拟参数:μ=0.5、σ=6、aA=0.5、r1=0.5;下同)
(16)
显然,通常有μ0<1/2且∂μ0/∂L<0。从而,可以得到结论:1.当居民对于工业品的偏好程度不太低,或者居民对于工业品的偏好程度较低但人口总量较大时,交易成本引致的集聚力超过了分散力,从而交易成本越高时城市人口越多;2.当居民对于工业品的偏好程度较低且人口总量较小时,交易成本引致的分散力超过了集聚力,从而交易成本越高时城市人口越少;3.交易成本对城市人口随着总人口增加而增长速率产生影响,交易成本越高则增长速率越快。
(二)经济空间边界
图3中,横轴和纵轴分别表示总人口L和经济空间边界f。在经济系统内总人口增加带来城市人口增加的同时,也带来农村人口的增加,从而导致经济空间边界的扩张。对均衡条件进行微分分析,可以得到,给定人口总量,交易成本对于经济空间边界的影响方向:
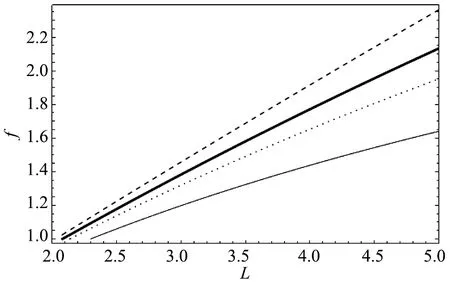
图3 人口规模与经济空间边界
∂f/∂τ>0⟺μ<μ0
(17)
可以得到结论:1.当居民对于工业品的偏好程度不太低,或者居民对于工业品的偏好程度较低但人口总量较大时,交易成本越高则农村人口越少,经济空间边界越小;2.当居民对于工业品的偏好程度较低且人口总量较小时,交易成本越高则农村人口越多,经济空间边界则越大;3.交易成本对农村人口及经济空间边界随着总人口的增加而增长的速率产生影响,交易成本越高则增长的速率越低。
(三)城市化水平
随着人口总量的增加,城市人口和农村人口均随之增加。但两者增长的速度有所不同,其效果可以通过城市化水平,即城市人口在总人口中所占比重来展示。图4中,横轴和纵轴分别表示总人口L和城市化水平sM,sM=2LM/L。如果总人口发生变化,那么城乡人口将会随之发生同向变化,但变化的速率有所不同,这将影响人口在城乡的空间布局,改变经济系统的城市化水平。由于城市经济更集约而农村经济依赖于土地,当人口总量增加时,城市人口增长速度超过了农村人口,城市化水平不断上升。

图4 人口规模与城市化水平
给定人口总量,交易成本对城市化水平的影响方向显然与其对城市人口的影响方向相同。因此:1.当居民对于工业品的偏好程度不太低,或者居民对于工业品的偏好程度较低但人口总量较大时,交易成本越高则城市化水平越高;2.当居民对于工业品的偏好程度较低且人口总量较小时,交易成本越高则城市化水平越低;3.交易成本随着人口总量的扩大而对于城市化水平的提升幅度产生影响,交易成本越高则提升幅度越大。
(四)工农业品价格⑤
图5中,横轴和纵轴分别表示总人口L和城市的农产品价格PA(r1)。随着总人口的增加,城市集聚了越来越多的人口,对农产品的需求也随之增加,从而提高了城市里农产品的价格。交易成本意味着农产品由产地运输到城市的价格增幅,因此,交易成本越高则城市的农产品价格越高;而且,交易成本较高时,城市的农产品价格随着人口增加而提高的速率较快。

图5 人口规模与城市的农产品价格
图6中,横轴和纵轴分别表示总人口L和城市的工业品价格指数PM(r1)。随着总人口的增加,城市集聚了越来越多的人口,工业品种类也随之增加,由于消费者的多样化偏好,这将降低城市里工业品的价格指数。交易成本对于城市的工业品价格指数有两方面的作用。一方面,提高交易成本会提升另一个城市的工业品在当地的销售价格;另一方面,当总人口增加时,交易成本越高则城市人口以及工业品种类数的增加速度可能越快,从而较快地降低工业品的价格指数。交易成本对于城市工业品价格的影响取决于这两方面效果的大小。对均衡条件进行微分分析,可以得到:

图6 人口规模与城市的工业品价格指数

(18)
显然,通常有∂μ1/∂f<0。因此:1.当居民对于工业品的偏好程度较高,或者虽然居民对于工业品的偏好程度较低但人口总量较大时,交易成本越高则城市的工业品价格越高;2.当居民对于工业品的偏好程度较低且人口总量较小时,交易成本越高则城市的工业品价格越低;3.交易成本对城市的工业品价格指数随着总人口的增加而降低的速率产生影响,交易成本越高则降低的速率越快。
(五)物价水平和居民福利
综合农产品和工业品价格的情况,可以得到物价水平的状况。人口规模对物价水平的影响是比较复杂的,当交易成本处于不同水平时,可能呈现出不同的特征。图7中,横轴和纵轴分别表示总人口L和城市的物价水平P(r1)。随着总人口的增加,城市里农产品价格提高而工业品价格降低;物价水平的变化取决于两部分价格变动幅度的高低。由于人口总量和经济空间边界正相关,从而可以计算P对于f的偏导:
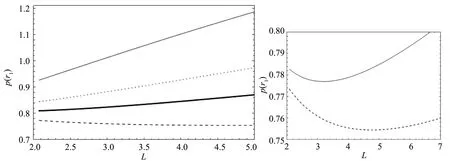
图7 人口规模与城市的物价指数
(19)
式(19)的右边包含两项,第一项显然为负数,而如果满足μ≥1-1/σ则第二项为非正,此时人口规模与居民福利水平正相关。但是,μ≥1-1/σ这一条件并不容易满足,通常情况下μ<1-1/σ,此时:1.当交易成本较高时,增加人口总量会提升城市的物价水平,提升速度随着交易成本的提高而增加;2.当交易成本较低时,人口总量的增加先降低再提高城市的物价水平。
城市物价水平的倒数等于城市居民的实际福利水平,VM=1/P(r1),由于福利均等化,这也是所有居民的实际福利水平。因此,当交易成本较高时,人口总量的增加降低了城乡居民的实际福利水平,降低速度随着交易成本的提高而增加;当交易成本较低时,人口总量的增加则可能先提升后降低城乡居民的实际福利水平。这一结论与Fujita(1995)[7]对于单城市经济的分析一致。根据式(19)可以判断,拐点的人口规模(及城市人口规模)随着交易成本的减少而增加,如图8、图9所示。
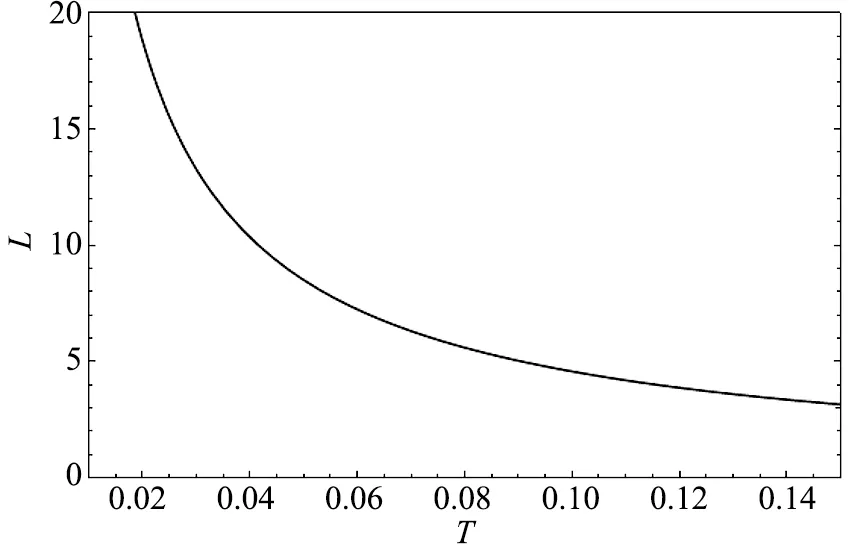
图8 交易成本与最优人口规模
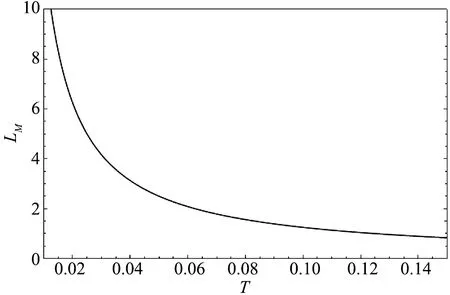
图9 交易成本与最优城市人口规模
这意味着,当交易成本较高时,过多的人口主要表现为社会的“负担”。随着交易成本的降低,人口对于社会的“负担”属性减弱,“资源”属性增强。而当交易成本较低时,人口总量在一定范围内,人口的“资源”属性超过了“负担”属性;从而,存在最优的人口规模(及城市人口规模),此时居民实际福利水平最高;随着交易成本的降低,“资源”属性占优的人口范围在扩大。
三、结论和启示
本文发展了以连续、线性空间为特征的NEG城市体系模型,探讨对称双城市的城乡结构下,随着交易成本的变化,城乡空间经济受到人口总量变化的影响。理论研究的结论认为:
1.人口总量的增加扩大了经济空间的边界,且同时增加了城乡人口,但城市人口增速更快,从而城市化水平随着人口总量的增加而上升。通常情况下⑥,城市人口和城市化水平随着人口总量的增加而提升的速度均随着交易成本的增加而提升,而农村人口和经济空间边界则正好相反。
2.城市的农产品价格随着人口规模的增加而提高,而工业品价格指数则随着人口规模的增加而降低,两者的变化率均随着交易成本的增加而提升。城市的物价水平随着人口总量的增加而变化也受到交易成本的影响;交易成本较大时,城市物价水平随着人口总量的增加而提升的速度也较快;交易成本较小时,随着人口总量的增加,城市的物价水平先降低后提高。
3.在交易成本较高时,城乡居民的实际福利水平随着人口总量的增加而降低;交易成本越高则降低得越快。交易成本较低时,随着人口总量的增加,城乡居民的实际福利水平先提升后降低;此时,存在人口总量及城市人口的最优规模,最优规模随着交易成本的降低而扩大。
本文得到的结论提供了一些启示:
1.相比于农业而言,城市经济对土地的依赖程度较低,城市可以容纳更多的人口,人口总量和城市化水平呈现显著正相关。一个经济区对人口的吸引力,首先反映到城市经济上。如果经济区不断成长,首先发展的是城市经济;反之,如果经济区衰退,首先萎缩的也是城市。
2.人口规模对于一个经济社会而言是“资源”还是“负担”,取决于交易成本的大小。交易成本越大,人口越表现为社会的“负担”;反之,交易成本越小,人口越表现为社会的“资源”。近年来,随着信息网络化的“新工业革命”,以及大规模的基础设施建设,我国整体的交易成本大幅降低,从而人口的“资源”属性愈发凸显。这成了各地追逐人才(人口)的一大动因。
3.交易成本今后仍将持续降低,从而城市可以容纳更多的人口,这也将提升居民的生活质量。降低交易成本是城市化的重要推动力,也是改变城市体系空间结构的重要因素。
注释:
①如果用G(r)表示产品出售到相距r单位远的地区剩下的产品,并给定G(0),从而有dG(r)/dr=-τG(r)⟹G(r)=e-τrG(0)。
②农村地区的农产品生产量超出了自己的消费量,因此农村地区的农产品价格实际上指的是其“价值”。
③借鉴Bosker等(2012)[15]对于中国经济状况的参数标定:μ≈0.5、σ≈6。
④数值模拟中设定了人口总量的下限,以保证在给定的各交易成本下经济空间是连续而非间断的,即避免由于人口太少而形成的城市之间的“无人区”。
⑤由于本文以城市的名义工资为计价物标准,从而所有名义价格水平为城市的名义工资的相对值。
⑥居民对于工业品的偏好程度不太低,或者居民对于工业品的偏好程度较低但人口总量较大。

