一种基于强化学习的绞吸挖泥船施工参数智能自主寻优方法研究

鲁嘉俊，杨波，徐婷

（中交疏浚技术装备国家工程研究中心有限公司，上海 201208）

0 引言

绞吸挖泥船是挖泥船中挖掘土质最广泛，排岸距离变化最大的一种吸扬式挖泥船[1]。目前，我国绞吸挖泥船的疏浚作业基本还停留在手工操作模式，在疏浚作业过程中，作业参数主要由操作人员根据自己的经验、试挖情况以及挖泥船的实际作业效果灵活确定[2]。为了降低人工成本并提升疏浚效率，丁树友等[3]开发了绞吸挖泥船智能型无人操控自动挖泥控制系统软件，软件功能包含集成监控功能与自动挖泥功能两部分，实现了疏浚作业过程的无人操控，但缺乏疏浚参数的自主寻优功能。Changyun Wei等提出了一种基于强化学习的绞吸式挖泥船智能优化控制策略，利用神经网络的泛化能力建立横移过程的动态模型，分别采用强化学习Sarsa算法[4]和Sarsa-Lambda算法[5]开发绞吸船摆动过程中的智能决策方法，并仿真验证了强化学习方法能成功模仿经验丰富的人工操作员的疏浚行为。但Sarsa算法和Sarsa-Lambda算法均受限于缓慢的收敛速度，且对状态空间要求必须是离散的且空间较小。相关的研究还有利用强化学习的智能体感知环境并经过自学习选择绞吸挖泥船横移过程的最优动作[6]，基于深度强化学习的绞吸挖泥船横移过程控制方法[7]，横移过程线性二次型产量最优控制方法[8]等，但以上研究均只考虑了疏浚过程的横移问题。

本文利用强化学习policy gradient算法在连续动作空间中更高效、收敛速度快的优势，提出了一种基于强化学习的绞吸式挖泥船施工参数自主寻优方法。利用机器学习的方法寻求疏浚过程的最佳作业参数，实现疏浚过程的自主分析与决策，可为疏浚技术的智能化发展提供思路参考[9]。

1 绞吸船强化学习模型设计

1.1 绞吸挖泥船理论模型

绞吸挖泥船是疏浚工程中使用数量最多的挖泥船，在疏浚施工中，瞬时产量是评价挖泥船性能最重要的指标之一，其直接决定了疏浚工程的效益[10]。绞吸挖泥船的瞬时产量计算公式为：

式中：W为瞬时产量；r为排泥管直径；v为管道流速；Cw为泥浆浓度。其中管道流速在挖泥过程中变化较小，所以泥浆浓度可直接反映产量情况。在疏浚作业中，泥浆浓度由绞刀切削泥土的体积量决定。

在挖掘过程中，实际切削的体积与纵向切泥厚度（由台车推进距离决定）、垂直切泥厚度（由斗桥位置决定）和横移速度有关：

式中：Vc为单位时间泥沙体积量；Bc为切削宽度，又称为纵向切泥厚度；Dc为切削深度，又称为垂直方向切泥厚度；Vs为挖泥船的横移速度，在传感器采集数据中主要表现为左/右横移绞车转速或左/右横移绳速。

在正常疏浚情况下，单位时间内绞刀切削泥沙体积按式（3）进行换算：

式中：K为绞刀挖掘系数，取0.8～0.9[11]；Vm为单位时间进入管道的泥沙体积。在管道输送中水下泵转速和甲板泵或舱内泵转速也会对泥沙输送流速产生一定的影响。

通过式（1）～式（3）可知绞刀转速、横移速度、泥泵转速、步进距离、桥架下放深度等均对瞬时产量产生影响。但在实际施工过程中，现场作业环境多变，控制参数与实际操作下输出量的关系不明确，难以用传统的理论研究和数学物理方法搭建绞吸挖泥船的疏浚作业过程模型[12]。而通过强化学习的方法来开展相关研究并建立其仿真环境模型，然后利用强化学习的自学习能力获取知识，改进行动方案并适应环境，具备较强的优势。

1.2 强化学习Policy Gradient算法

Policy Gradient算法是一种基于策略的算法[13]，相对于基于值函数的强化学习方法通过引入动作价值函数Q（s，a），策略梯度（Policy Gradient，PG）采用回合更新的方式，通过不断调整参数θ实现策略πθ（s，a）的优化更新，收敛速度更快[14]。

为了评估不同参数对策略πθ（s，a）的影响，引入目标函数，目标函数的值越大，模型质量越高。目标函数主要有3种形式：使用初始状态的期望为优化目标（式（4））；对于连续性任务，没有明确的初始状态，优化目标是平均价值（式（5））；将每一时间步的平均奖励作为优化目标（式（6））。

本次研究采用式（6）作为目标函数。在策略函数πθ的设计上，采用连续动作空间的高斯策略（Gaussian Policy）：

J（θ）考虑单步的马尔科夫过程，R（s，a）考虑奖励函数，对目标函数求导得到式（8），即对目标函数J（θ）求导最终转化为对策略πθ求梯度。在Policy Gradient算法中，策略πθ按式（9）进行参数更新：

2 基于强化学习的绞吸挖泥船疏浚参数自主寻优方法

2.1 数据预处理

1）kalman滤波

绞吸挖泥船上的大部分信号采集装置在信号产生、转换、传输的各个环节中易受供电电源及现场施工条件干扰，导致这些信号点存储的数据中包含噪声和干扰信号，因此有必要对采集的实船数值进行滤波。在滤波方法的选择上，本次研究尝试卡尔曼滤波、移动平均滤波、中值滤波、维纳滤波等多种方法。对比发现卡尔曼相比其他滤波方法更为平稳，能够剔除尖刺并反映样本的整体趋势。

2）数据切割

绞吸挖泥船在步进和换桩过程中，瞬时产量是偏低的。为了更精确分析绞吸挖泥船的瞬时产量，筛选出横移周期内的有效数据，本次研究采用自动搜索算法寻找绞刀至右边线距离的所有谷/峰值，在图1中用圆圈进行标记。然后用阈值过滤非正常的点，即绞刀头到边线上距离小于5 m，或者大于85 m的时段，并取相邻峰谷值之间的时间作为一个横移周期。

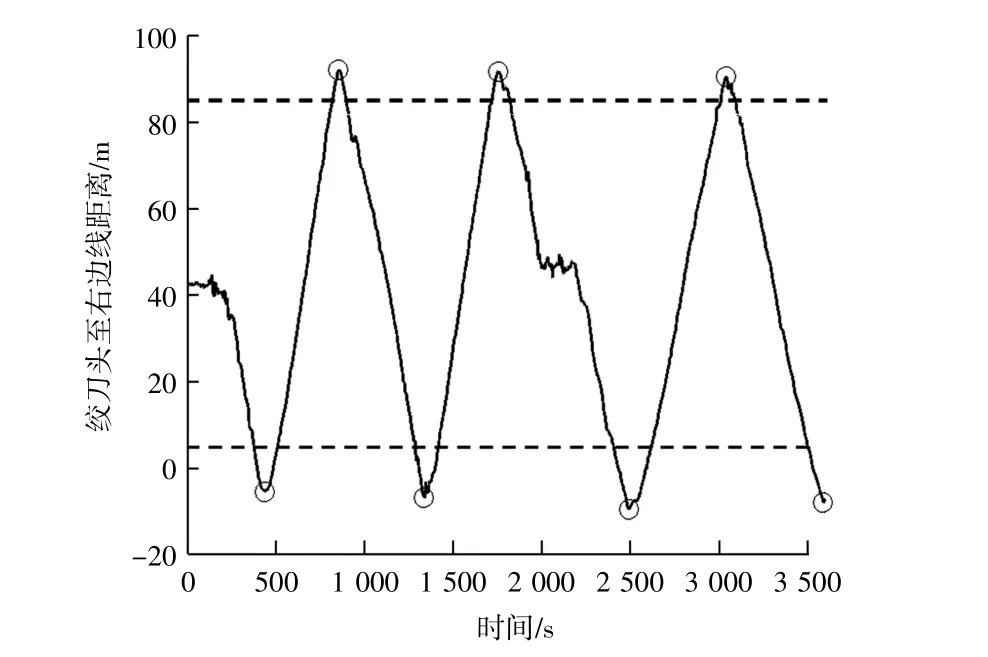
图1 横移周期选取Fig.1 Selection of traverse period

2.2 瞬时产量时滞分析

建立管道内的流速分布函数，根据管道长度及流速的动态变化分别计算出泥水混合物通过吸入管、连接管、竖直管的时间，得到瞬时产量的时间延迟为31 s。然后随机选取500 s连续数据，验证瞬时产量的延时时间，结果见图2。其中瞬时产量值为时间往前拉31 s的产量值，图中可见真空度与后31 s的瞬时产量相关性较高，且变化趋势一致。

图2 瞬时产量时滞分析图Fig.2 Time-delay analysis of instantaneous production

2.3 强化学习环境模型构建

在疏浚施工过程中，影响绞吸挖泥船瞬时产量的因素众多，本次研究将重点放在疏浚员能操纵的控制变量上，在瞬时产量影响因素的特征筛选中使用信息增益率的方法[15]对传感器采集的数据样本进行降维。信息增益是指添加了信息之后能增加多少收益，也即增加信息之后能减少多少不确定性。信息增益率在信息增益的基础上，除以一个分裂信息量，计算节点上样本总的信息熵。信息增益率方法经常被用来判断变量的重要性，利用该方法筛选出和瞬时产量密切相关并可人工调控的参数为水下泵转速、甲板泵或舱内泵转速、绞刀转速、左横移绳速和右横移绳速。各控制变量的信息增益率见表1。

表1 各控制变量信息增益率Table 1 Information gain rate of control variables

筛选出控制变量后，定义动作区间action=[水下泵转速，甲板泵或舱内泵转速，绞刀转速，左横移绳速，右横移绳速]，即强化学习中智能体可以控制的变量。同时，设置各控制参数的上下限区间。该动作区间为连续动作空间，可以满足动作区间完备性、高效性、合法性的要求。

强化学习智能体执行当前动作作用到环境，环境反馈对应状态值，并将其与奖励值反馈智能体，与此同时环境转移到下一个状态。由此得到强化学习的行动状态序列：

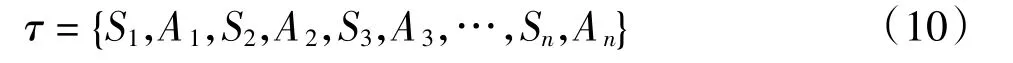
奖惩函数的定义见式（11）：

式中：R表示智能体执行动作所获得的奖励值，即对当前动作好坏的评价；O代表绞吸船瞬时产量，瞬时产量越高学习系统得到的奖励值相对也越高；D为该时刻的控制参数与上一时刻控制参数的欧氏距离偏差，加入此变量是为了限制两次输入信号之间的变化幅度，防止控制参数剧烈跳变；Dc为D的乘数项系数，默认值为100；Pf定义为惩罚函数，若系统控制变量超限，则给予智能体惩罚值。

2.4 强化学习仿真结果与分析

本次学习共选取7万个实船数据点，设置训练回合数1000，折扣率γ=0.99。随着训练进行，好的动作被选取的概率逐渐增大，不好的动作慢慢淘汰，同时奖励值渐渐上升，代表着智能体在自学习过程中逐步获得最佳施工参数。

机器学习中每回合奖励值变化见图3。

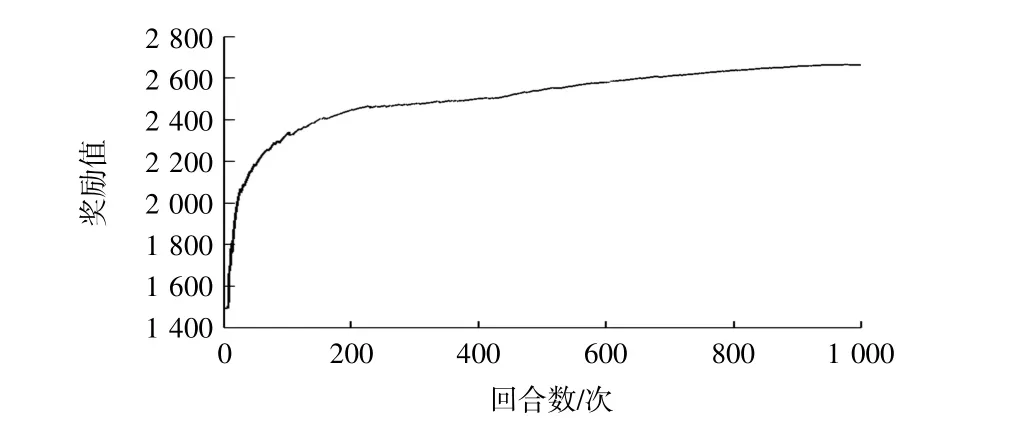
图3 奖励值变化图Fig.3 Reward value change chart

训练结束后，通过控制仿真试验得到强化学习控制结果，与实际人工操作进行对比，结果见图4。1）瞬时产量对比图4（a）：采用强化学习最优参数控制的瞬时产量比人工操作时高，且可将瞬时产量值维持在高点，可以稳定有效提高挖泥船的疏浚产量；2）水下泵转速对比图4（b）：与人工操作相比，强化学习推荐的水下泵转速波动更小，基本稳定保持在228和232之间；3）甲板泵或舱内泵转速对比图4（c）：强化学习推荐的甲板泵或舱内泵转速普遍低于人工操作水平，能耗较小；4）绞刀转速对比图4（d）：相比人工操作，强化学习推荐的绞刀转速更加稳定高效；5）左横移绳速对比图4（e）：强化学习推荐的左横移绳速无剧烈波动，从长期时间来看，左横移绳速基本在[2，18]之间，而人工控制的左横移绳速区间在[0，25]，且时常出现跳变的情形；6）右横移绳速对比图4（f）：同左横移绳速。

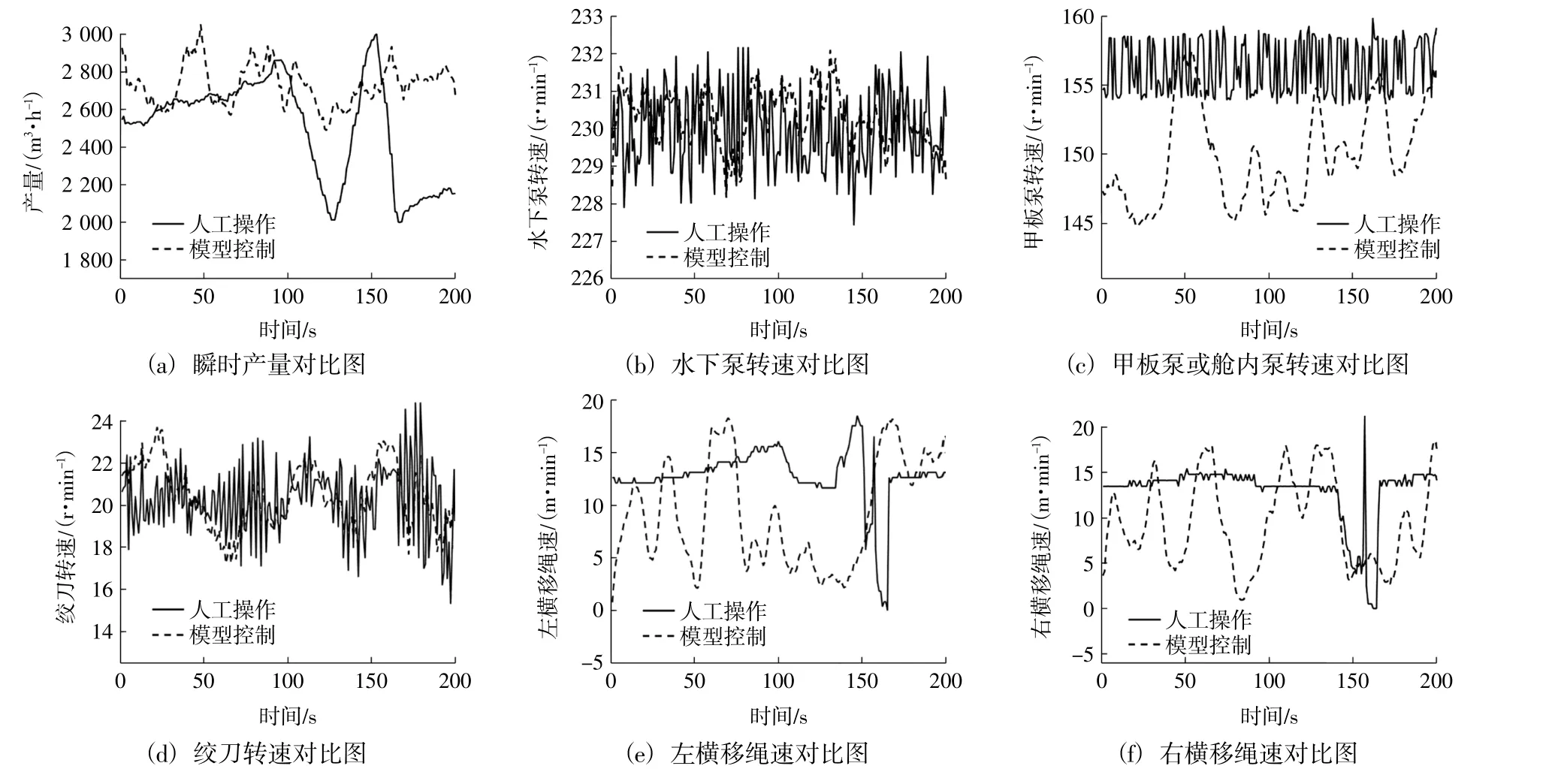
图4 模型控制与人工操作结果对比图Fig.4 Results comparison of model control and manual operation

3 结语

1）同种工况下，采用智能自主寻优的疏浚参数可以使瞬时产量高于人工操作的平均水平，且泥泵、绞刀和横移绞车的参数变化更加平缓，效率更优。该智能自主寻优方法可为绞吸挖泥船实现智能疏浚提供理论依据和技术参考。

2）为了保障施工安全，设置强化学习环境模型中控制参数的上下限区间，添加控制变量超限的惩罚函数，由此使得强化学习推荐的最佳施工参数均位于安全区间。

3）寻优后的参数能快速响应动态的环境变化，深层次原因是智能体能够评估当前状态，并寻找使得未来回报最大化的策略，从而灵活调整控制参数，使得预期收益最大化。相比而言，操作员决策依赖于操作面板的数据，缺少对未来的预测判断。

4）下一步计划研究多船多工况下绞吸挖泥船的智能优化控制方法，并在实船中应用。