基于位置预测的多MEC服务器协同卸载算法

王 翊，卢兴俊，许耀华，蒋 芳

(安徽大学计算智能与信号处理教育部重点实验室，安徽 合肥 230601)

随着5G技术的快速发展普及，很多计算密集型的移动应用为用户提供了优质的服务体验，如人脸／语言识别、高清视频流、实时在线游戏、虚拟现实等［1］。由于移动终端的计算能力与存储容量有限，移动用户在获得高质量服务的同时，会面临高能耗的挑战［2］。移动云计算将计算任务卸载到远程云缓解终端计算压力，但数据传输时间长，在实际运用中无法满足超高速率的用户需求。移动边缘计算（Mobile Edge Computing，MEC）可在移动网边缘提供服务环境和计算能力，减少网络操作和服务交付的时延，提高用户体验［3］。MEC服务器的超高计算能力和超低时延，使其成为新一代移动通信的关键技术［4］。

在处理计算密集型任务［5］时，MEC主要通过计算卸载和资源分配来有效降低时延和能耗。文献［6］研究MEC超密集网络中的任务卸载问题，采用软件定义网络的思想，提出一种有效的计算卸载策略，以达到任务处理时延最小的目的。文献［7］提出了一种联合优化资源分配和任务卸载分配的策略，保持算法低复杂度并减小了设备能耗。部分学者针对边缘计算系统时延和能耗两个方面进行优化，设定时延和能耗的相关权重系数，根据不同的场景改变权重数值。文献［8］研究了多MEC服务器的边缘计算系统的任务卸载和资源联合优化问题，考虑了基站重叠覆盖的情况，通过多服务器卸载策略、上行功率分配策略、资源分配策略的联合优化，最大化权衡后的综合效用。上述文献采用不同算法制定卸载策略对有限的计算资源进行分配，但是忽视了终端设备的移动性对卸载决策的影响。

由于服务器的覆盖范围有限，用户在移动的时候可能会中断与服务器的连接。原先请求卸载的服务器无法在用户的下一位置及时发送计算结果，会引起服务器计算资源的浪费，增加用户再次上传卸载计算任务的时延和能耗。因此，对用户设备的未来位置进行预测显得尤为重要。文献［9］通过预测用户的移动对虚拟机的迁移策略进行优化，并提出了基于用户移动性的服务迁移预测方案，对迁移成本和服务质量采取了折中的办法。但是对于一些即时性要求较高且任务量较小的应用程序，迁移成本过大。文献［10］通过长短期记忆方法建立用户位置预测模型，位置预测的结果更接近真实位置，但是需要复杂的特征数据，难以用于普通场景。文献［11］通过对用户移动性的预测，在收集任务处理结果时确定终端与边缘服务器的连接性，从而决定将任务分配到哪一个边缘服务器。但其用户运动模型是线性的，没有考虑用户移动中存在加速度的情况，为符合实际应用，本文将在研究中考虑存在加速度的场景。

对于用户的可卸载任务，许多研究都会采取全部卸载到MEC服务器中执行的方式［12-13］。但是当用户数量较多或卸载任务量较大时，有限的服务器计算资源会导致任务排队，卸载计算时延增长。文献［14］给出了部分卸载的办法，将一部分任务留在移动终端，减少MEC服务器的计算量，并利用KKT条件来解决能耗最小化问题。文献［15］对能量收集时间、局部计算频率、卸载时间和功率进行联合优化，提高计算效率。但是上述研究只将任务卸载到一个MEC服务器，当服务器负载较大或者卸载任务量较大时，计算时延依旧会较大。并且网络中的MEC服务器负载状况不同，部分服务器的计算资源可能未被充分利用，为了解决以上问题，文献［16］利用网络中多个可用边缘节点并行处理卸载任务。本文将卸载任务划分为多个子任务，并由移动用户与多个服务器协同处理。

卡尔曼滤波（Kalman Filter，KF）作为一种对系统状态进行估计的算法，具有较低的时间复杂度和空间复杂度，在移动网络的资源分配与网络状态估计中也有应用［17-19］。但是其仅适用于线性系统，当系统为非线性时，更适用改进后的卡尔曼滤波，即扩展卡尔曼滤波（Extended Kalman Filter，EKF）。 但目前尚未应用于MEC计算卸载的研究中，本文将利用扩展卡尔曼滤波解决进行非线性移动的用户的计算卸载问题。

根据密集网络中小基站数量众多的特点，本文的研究场景建立在一个分布式的多MEC服务器系统中，提出了一种基于位置预测的多MEC服务器协同卸载算法，通过预测移动用户的未来位置和划分卸载任务来降低计算卸载的时延和能耗。本文的主要工作有：

（1）首先针对非匀速运动的用户建立非线性运动模型，再采用扩展卡尔曼滤波的方法预测用户的未来位置，提高移动用户与MEC服务器的连接成功率，有效避免用户跨越MEC服务器覆盖区时传输中断。

（2）在用户位置预测的基础上，将用户的卸载任务划分为多个子任务，交由用户移动路径上的MEC服务器协同处理，任务划分以最优化任务处理时延和能耗加权和为目标。最终的计算结果提前发送到离用户预测位置最近的服务器，随后转发给用户，有效降低时延和能耗。

1 移动用户的任务协同卸载模型

1.1 系统模型

在图1所示的系统模型中，有一个移动用户和多个无线接入点，每个无线接入点连接一台MEC服务器。用户移动性的预测是在服务器或终端本身进行的，将用户发送卸载请求的位置作为当前位置，利用当前位置信息与运动状态预测的用户下一位置作为预测位置。用户在请求位置处向服务器m1所在的无线接入点发送卸载任务，服务器m1接收到卸载任务后，根据任务的处理时间和能耗将其划分为多个子任务，并联合附近的服务器对任务进行处理，最后将处理结果通过预测位置处的无线接入点发送给用户。根据用户的移动路径，可能会有多个MEC服务器参与到卸载任务的处理与传输中。

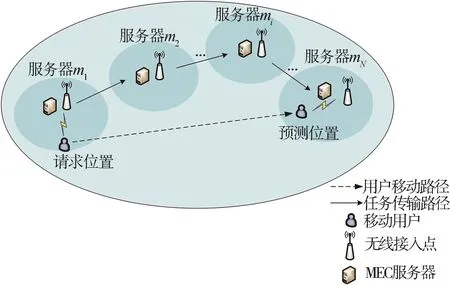
图1 系统模型

设移动用户u移动路径周围有N个MEC服务器，构成服务器集M＝｛m1，m2，m3，…，mi，…，mN｝，i∈［1，N］。 用户需要计算的任务d＝｛c，b｝，c表示任务所需的计算CPU周期数，b是任务卸载过程中所传输的数据量。将任务d划分为N＋1个子任务，即d＝｛d0，d1，d2，…，dj，…，dN｝，j∈［0，N］，其中第j个子任务dj＝δjd，δj表示任务的划分比例，即用户卸载到服务器mi的任务占总任务的比例。

1.2 通信模型

MEC服务器在靠近用户的网络边缘侧提供计算服务，分布范围广且部署灵活。本文中，每个MEC服务器连接一个无线接入点，卸载任务通过无线回传链路在移动用户与MEC服务器间、MEC服务器与MEC服务器间传输。设部分子任务由本地计算，另一部分则由MEC服务器计算。用户u到最近服务器m1的上行链路传输速率是ru，m1，表达式为

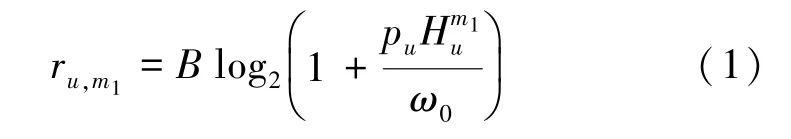
式中：B为信道带宽，pu为用户的传输功率，为用户到最近服务器m1的信道增益，ω0为噪声功率。

假设参数β1代表任务的划分开销因子，即划分任务时产生的额外计算量，β2代表车辆上行链路的传输开销因子，用表示子任务dj从移动用户u到服务器m1的上行链路传输时间，则

1.3 计算模型

1.3.1 本地计算

用户在本地计算的部分任务即为d0，本地可以处理的最大计算量为，计算d0所需时间为是移动用户的稳定处理速度（每秒处理的计算量）。d0的计算能耗为， 其中λ0表示移动设备上每CPU周期消耗能量的系数。

1.3.2 卸载计算

假设用户的卸载任务从当前位置传输到预测位置涉及到N个服务器，则用户卸载的任务可分为N＋1个子任务，由用户与N个服务器协同处理。考虑到MEC服务器的计算资源有限，划分到MEC服务器的子任务不超过服务器可以处理的最大计算量。根据每个子任务各自处理的时延和能耗，选取一个使任务的整体能耗和时延加权和最小的划分比例。子任务dj选择在服务器mi执行，服务器可以处理的最大计算量为则计算子任务dj消耗的时间为，其中fm是服务器的稳定处理速度。

2 基于位置预测的协同卸载算法

2.1 基于扩展卡尔曼滤波的位置预测方法

考虑用户进行非线性运动，k时刻的真实状态向量可以表示为sk＝［lx，vx，ax，ly，vy，ay］T， 其中lx、vx、ax表示二维平面中横坐标方向上的位置、速度、加速度，ly、vy、ay表示二维平面中纵坐标方向上的位置、速度、加速度。

经过时间Δt后，用户移动到新的位置，用户的运动状态可以通过以下运动方程得到

式中，v＝v0＋a·Δt。

在系统的状态空间中，状态变量每时每刻都在变化，可以由状态转移方程表示为

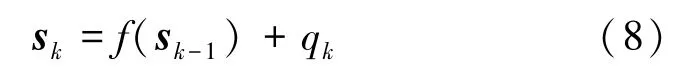
式中：sk-1表示k-1时刻的真实状态向量；f（·）为非线性系统中的状态转移函数；qk是状态噪声，假定均值为0，协方差矩阵为Qk＝cov（qk），服从正态分布，即：qk～N（0，Qk）。

系统中状态测量方程是将隐含的真实状态空间映射到测量空间，表示为

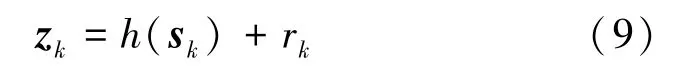
式中：zk为测量向量，是状态向量的映射；h（·）为测量函数；rk为状态噪声，假定均值为0，协方差矩阵为Rk＝cov（rk），服从正态分布，即：rk～N（0，Rk）。

假设在每一时隙中，用户的运动状态与前一状态保持一致，仅在下一状态发生改变。采用扩展卡尔曼滤波方法，根据移动用户当前时刻的状态值（速度、加速度），通过预测和测量反馈两个步骤，实现对用户未来时刻位置的预测。

（1）线性化系统：利用泰勒级数将非线性方程展开，略去高阶项，转换成线性系统。

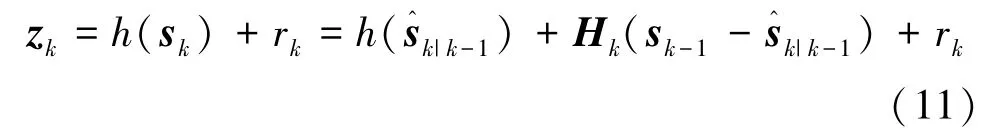
（2）滤波过程：进行扩展卡尔曼滤波中的预测和测量反馈。如图2所示，系统初始化后，首先在预测阶段，通过k-1时刻的状态值计算k时刻的预测值以及预测值和真实值的误差协方差Pk｜k-1；在测量反馈阶段，先计算卡尔曼增益Kk，并根据测量值修正此时的状态值得到，然后计算估计值与真实值之间的误差协方差Pk用于下一次递推，直到状态值为最优估计值。

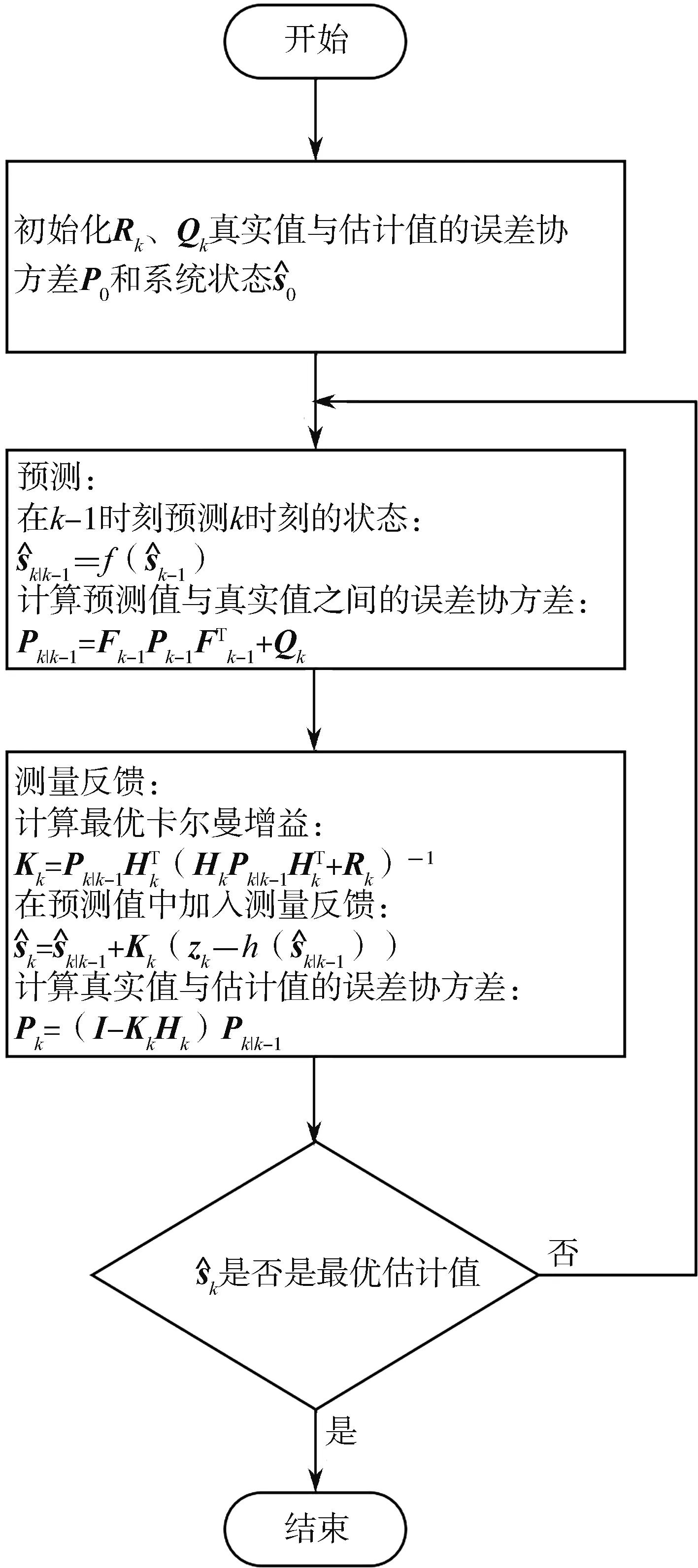
图2 位置预测方法的扩展卡尔曼滤波流程图

2.2 协同卸载效用函数及优化方法

根据第1节中对系统模型的描述，当用户移动到某服务器的覆盖区域时，可以与该服务器建立无线连接，并将需要卸载的任务传输到服务器上。卸载延迟包括4个部分：上行链路通信延迟、回程链路延迟、下行链路通信延迟和任务处理延迟。由于回程链路延迟远小于上行链路，且下行链路传输的数据量远小于上行链路，所以在分析的时候忽略了这两种延迟，只考虑上行链路通信延迟和任务处理延迟。当计算任务和任务处理结果在服务器间传输时，由于任务处理结果数据量远小于计算任务的数据量，所以只考虑上行链路通信延迟。此外，由于本研究是从用户的角度考虑能耗和时延，故服务器的计算能耗不包括在内。

根据实际应用分析，优化目标相当于在限制条件的约束下最小化式（14）给出的效用函数φ（δ），由移动用户做出关于计算任务划分比例的决策。该问题可以表述为

对于∀i∈［1，N］，C2表示计算密集型任务划分成子任务的比例，C3表示由移动终端处理的子任务计算量不超过移动终端可处理的最大量，C4表示卸载到MEC服务器的子任务计算量不超过服务器可处理的最大量。

在本文的优化模型中，自变量δ的约束条件为线性等式和线性不等式，系统效用模型为有约束的线性优化问题。考虑到单纯形法对变量和约束数量不多的线性规划问题有较好性能，因此将成为前述问题的优化求解算法。求解可分为以下3步：（1）求一个初始基本可行解；（2）检查该基本可行解是否为最优解；（3）若是最优解，则为线性优化问题的解，若不是最优解，则设法再求一个不同的基本可行解，并重复步骤1、2。

首先，为将线性规划问题化为标准型，引入松弛变量 δ′0、δ′j、δ″j， 将约束 C3、C4、C5改写为

其中，CY为非基本变量系数，CB为基本变量系数，B为基，Y为非基向量组。如果所有检验数大于0，则为最优解，否则需要另求一个不同的基本可行解。

为求得一个不同的基本可行解，需要选择一个在目标函数里系数为负的非基本变量δe（入基变量），将δe用基本变量δl（替出变量）表示，然后把δe变为基本变量，δl变为非基本变量。替入变量对应的检验数是所有检验数中最小的。

把已确定的入基变量在各约束方程中的数除其所在约束方程中的常数项，把最小比值所在的约束方程中的原基变量确定为替出变量。假设该比值为θ，则有

换基后，重复以上步骤，直到当前各非基变量的检验数大于0，找到最优解。通过以上的单纯形法对式（15）进行优化，得到的结果在下一节进行仿真分析。

3 仿真结果与分析

3.1 参数设置

本节将利用仿真对基于位置预测的多MEC服务器协同卸载算法进行性能评估。MEC广泛分布于网络边缘，为了便于研究，仿真场景选取了一个半径为200 m的小区，小区中设置了多个服务器，分布在不同位置，彼此通过无线回传链路通信。若用户移动进入新的小区，则会重新启动新小区的协同卸载算法。仿真参数如表1所示。

表1 仿真参数表

3.2 仿真分析

3.2.1 效用函数性能仿真分析

仿真中考虑了两个对比算法：对比算法1［20］是无预测的任务划分算法，不考虑用户的移动，假设有两个MEC服务器参与到计算中；对比算法2［21］是无预测的任务卸载算法，综合考虑任务处理的时延和能耗，选择在本地处理计算任务或者选择一个最优服务器进行卸载。

图3表示了任务数据量对效用函数的影响，设定用户移动初始速度为60 km／h，加速度为2 m／s2，小区内服务器数量为20个。从图中可以看出，随着任务数据量的增加，3种算法的效用值都在增加。其中，数据量在0到6×108bit时，3种算法效用值都保持稳定增加。对比算法1在数据量达到6×108bit后明显增加，而本文所提出的方法一直保持稳定较低的效用值，比对比算法1的效用值低15.29%。这是因为考虑到用户移动后，参与计算的服务器数量随用户移动距离的增大而变多。相较于对比算法2，本文算法的效用值平均低33.10%左右，这是因为本文算法将计算任务优先分配给离请求位置较近的若干服务器，减小了计算任务的排队时间，因此有较低的效用值。

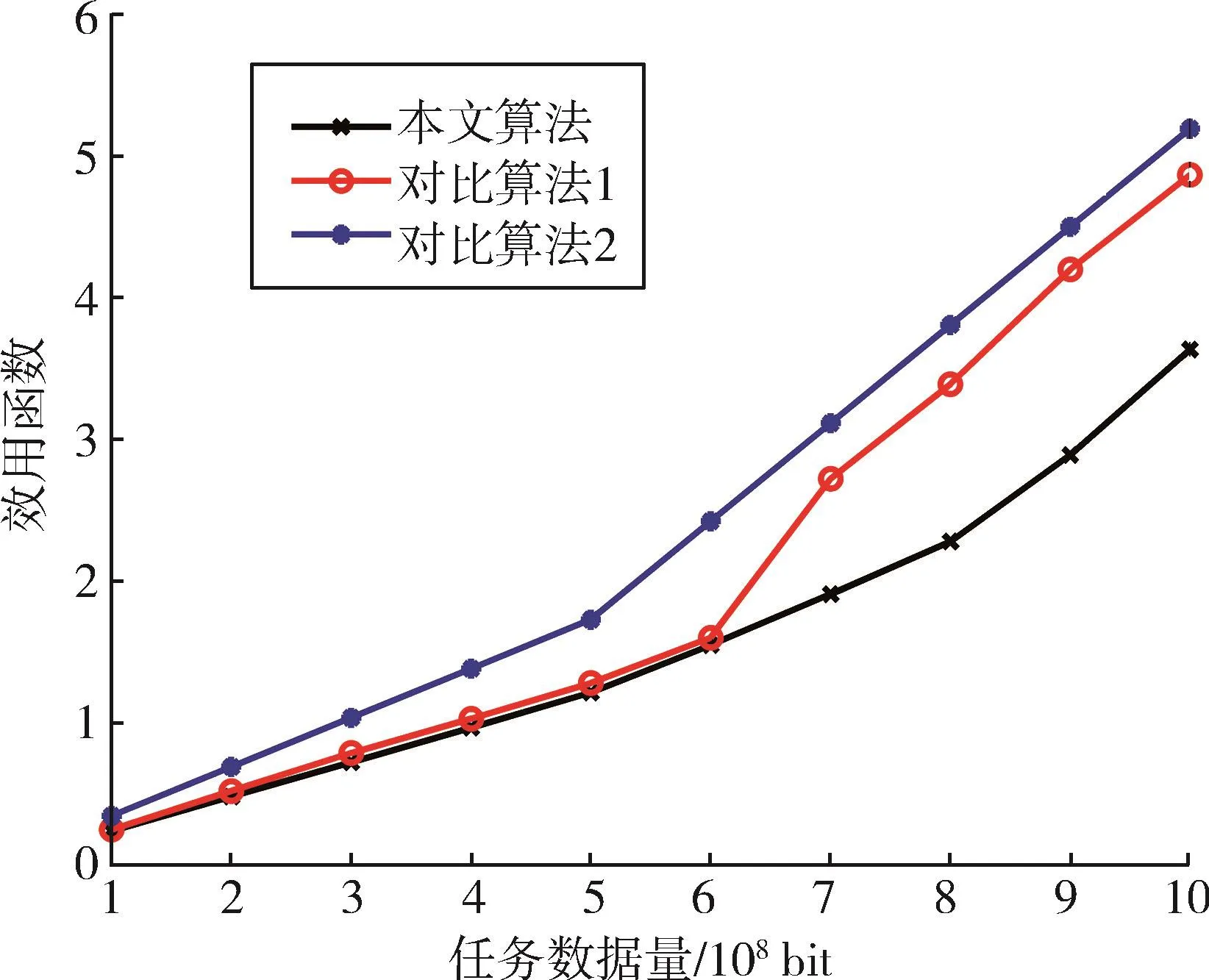
图3 任务数据量对效用函数的影响

图4表示了MEC服务器计算资源容量对效用值的影响，设定用户移动的初始速度为60 km／h，加速度为2 m／s2，任务量为 5×108bit，小区内 MEC 服务器数量为20个。从图中可以看出，随着服务器计算资源容量的增加，3种算法的效用值都在减小，且本文算法的效用值一直最低。相较于对比算法1，本文由多个服务器协同卸载，减小了计算任务的传输和计算时延；而对比算法2只选择一个MEC服务器处理卸载任务，当服务器计算资源容量有限时，任务排队等待的时间会较长。由此得出，在计算资源受限时，本文算法通过灵活选择多个MEC服务器处理计算任务，有效降低了任务处理的时延和能耗，相较于其他两种算法优势较为明显。

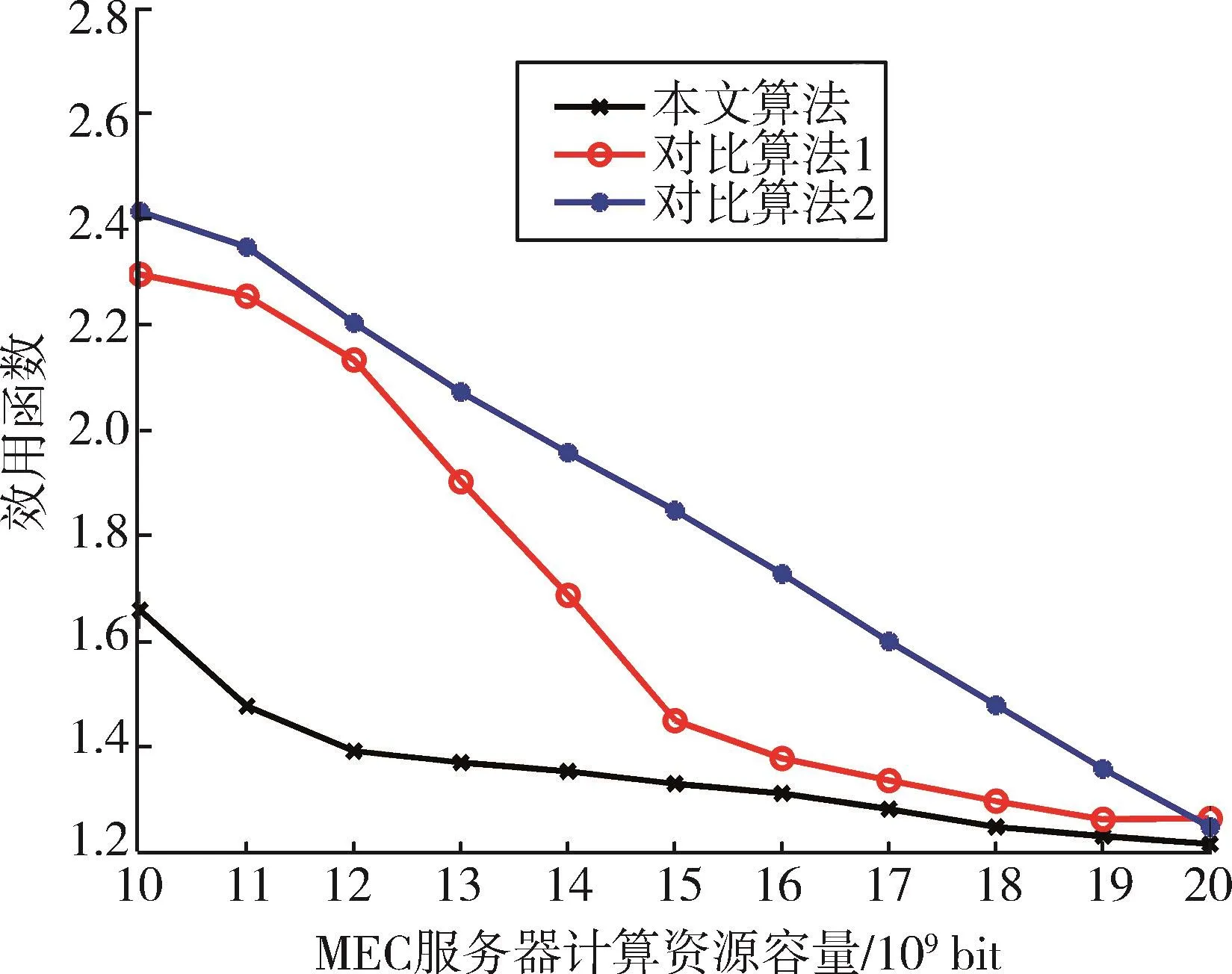
图4 MEC服务器计算资源容量对效用函数的影响

3.2.2 位置预测成功率仿真分析

为体现位置预测成功率的性能，本小节将文献［13］提出的算法作为连接对比算法1，该算法使用了匀速运动模型，采用卡尔曼滤波方法预测用户的位置，但是没有考虑实际情况中用户运动加速度对预测结果的影响；连接对比算法2是无预测的卸载算法，只在用户请求卸载的位置选择最近的服务器卸载。

图5展示了在服务器数量为20个、加速度为2 m／s2时，用户初始速度对连接成功率的影响。随着速度的增加，用户移动的距离变长，但服务器的覆盖范围有限，因此连接的成功率会降低。本文算法与连接对比算法的连接成功率也随速度的增加而拉大差距。在初始速度为10 km／h时，本文算法连接成功率相较于对比算法1和对比算法2差距并不明显，当初始速度提高到100 km／h时，本文算法连接成功率相较于对比算法1和对比算法2分别提高13.06%和35.03%。这是因为连接对比算法1在预测时没有考虑到加速度对位置预测的影响，选择的服务器与用户真实位置较远。本文算法选择的服务器离用户真实位置较近，连接成功率更高；连接对比算法2选择的服务器是相对于请求服务位置最近的，用户移动后，连接成功率大大降低。

图5 用户初始速度对连接成功率的影响

图6表示了用户移动初始速度为60 km／h，加速度为2 m／s2时，连接成功率随服务器数量的增加而增加。当MEC服务器数量为5个时，本文算法连接成功率为48.41%，随着服务器数量的增加，本文算法连接成功率不断提高，当MEC服务器数量为25个时，本文算法连接成功率达到72.5%。这是因为服务器的数量增加使服务器分布更加密集，用户与服务器之间的距离变短，可选择的服务器数量增加。本文算法可以选择的卸载服务器数量较多，连接成功率相较于连接对比算法更高。

图6 服务器数量对连接成功率的影响

4 结束语

在MEC网络中服务器的计算资源受限的情况下，本文针对用户移动性带来的卸载任务传输延迟和能耗较大的问题，通过位置预测与任务划分相结合的方法降低了任务卸载的时延和能耗。将移动用户和服务器的总时延和总能耗作为优化目标，给出效用函数模型，提出一种基于位置预测的多MEC服务器协同卸载算法，将扩展卡尔曼滤波和单纯形法相结合对效用函数进行优化。仿真结果表明，本文算法相较于两种对比算法有更低的时延和能耗，且连接成功率更高。未来的研究中，将考虑小区中有多个移动用户竞争计算资源，对用户卸载的时延和能耗进行更好的优化。