气相17O核磁共振化学屏蔽常数与化学位移的理论研究

陈茹婷，吴安安

(厦门大学化学化工学院，福建省理论与计算化学重点实验室，福建 厦门 361005)

近年来，随着核磁共振(NMR)实验技术，特别是多维技术和去耦合技术的大力发展，17O-NMR波谱逐渐成为含氧化合物结构描述和鉴定的重要手段[1-2].目前，利用现代核磁技术已经可以从实验上获得可靠的17O化学屏蔽常数和化学位移，但在理论方面对于17O 化学屏蔽常数和化学位移仍缺乏系统的研究.一个主要的原因是含氧化合物通常具有较强的电子相关效应，采用传统的HF(Hartree-Fock)方法和MP2(Møller-Plesset)方法均无法获得令人满意的结果[3-4].要获得精确的计算结果就必须使用包含高阶电子相关效应的量子化学计算方法，如包含三重激发微扰校正的耦合簇(CCSD(T))方法[5].CCSD(T)结合规范不变原子轨道 (GIAO)技术[6-7]在使用大基组前提下能够给出足够精确的17O化学屏蔽常数和化学位移，然而计算量的限制使得其仅适用于小分子体系(通常小于7个重原子).本课题组近年提出了适用于磁性质计算的焦点分析(FPA-M)方法[8-10]，该方法对于元素周期表前两周期元素的计算精度接近于CCSD(T)/完全基组(CBS)的极限，但系统的研究显示FPA-M方法仅适用于不超过15个重原子的体系[9].因此，密度泛函理论(DFT)方法成为目前计算大分子体系化学屏蔽常数最常用的方法.然而传统的DFT方法在计算17O化学屏蔽常数时通常会产生较强的去屏蔽效应[11]，其计算结果与实验值存在较大的偏差.在21个分子的测试中，Auer[12]的研究显示，与气相实验值相比常用的B3LYP与BP86泛函均无法给出足够精确的预测，其平均绝对偏差(MAD)分别为20.6×10-6和20.3×10-6，仅与HF方法 (MAD为21.7×10-6)相当.为进一步提升DFT方法的计算精度，Stoychev等[13]发展了DSD-PBE86双杂化泛函，在很大程度上提高了DFT对气相17O化学屏蔽常数和化学位移的计算精度.最近，Zhang等[14]发展了针对13C化学位移计算优化的新泛函xOPBE，研究表明xOPBE泛函大大提升了OPBE泛函在13C-NMR化学位移中的计算精度，即使对于OPBE无法准确描述的1-金刚烷阳离子[9,15]也能达到CCSD(T)结合大基组的计算精度[15].鉴于xOPBE泛函在13C-NMR化学屏蔽常数和化学位移计算中的成功应用，本文将系统地研究xOPBE泛函在气相17O化学屏蔽常数和化学位移计算中的表现.

1 研究方法及研究体系

1.1 研究方法

本文中17O化学屏蔽常数的计算采用FPA-M[8-9]、xOPBE[14]、M06-L[16]、PBE0[17]、OPBE[18-19]、B3LYP[20-21]和MP2等方法，为解决化学屏蔽常数计算中的规范原点问题所有计算都采用GIAO技术[6-7].在DFT和MP2的计算中，基组采用Cheeseman等[22]推荐的6-311+G(2d,p)，FPA-M的计算中则采用Dunning等[23-24]开发的cc-pVnZ基组(n=D、T、Q和5，简写为VnZ).为消除分子构型对计算结果的影响，所有分子均在CCSD(T)/VTZ级别下进行构型优化.

FPA-M方法是在MP2/CBS的极限值上，增加CCSD(T)/VTZ与MP2/VTZ的差值作为高阶相关校正项，其屏蔽常数σe的计算公式如下：

σe(CCSD(T)/CBS)≈σe(MP2/CBS)+

Δσe(CCSD(T)),

(1)

Δσe(CCSD(T))≈σe(CCSD(T)/VTZ)-

σe(MP2/VTZ).

(2)

xOPBE是将OPBE泛函与HF交换相结合并在6-311+G(2d,p)基组下进行优化的新杂化泛函，计算公式如下：

EXC=αEX，HF+(1-α)EX,OPTX+EC,PBE,

(3)

其中EX,HF和EX,OPTX分别表示HF和OPTX的交换函数，EC,PBE表示PBE的相关函数,α=0.23代表数值参数.

本文中关于CCSD(T)方法的计算是在CFOUR[25]程序下完成的，DFT和MP2方法的计算则是采用Gaussian 16[26]程序完成的.

1.2 研究体系

本文研究的分子包含19个含氧化合物，如图1所示.这些分子均具有可靠的气相实验数据以及高精度的理论计算结果用于比较[27,12].

2 结果与讨论

2.1 17O化学屏蔽常数

Stoychev等[13]发展了DSD-PBE86双杂化泛函并对6个小分子(CO、H2O、F2O、NNO、CH3COCH3和C4H4O)的17O化学屏蔽常数进行了研究.为了系统地考察FPA-M和xOPBE方法，首先研究这6个小分子的气相17O化学屏蔽常数.

表1列出了xOPBE、DSD-PBE86、CCSD(T)/pz3d2f和FPA-M方法计算的化学屏蔽常数，及其相对于气相实验值的MAD和最大绝对偏差(MAX).需要强调的是，xOPBE在参数优化过程中已经考虑了振动转动对化学屏蔽常数的影响(振转校正Δσvib)，因此在计算中不需要额外考虑振转校正，而其他方法则不能忽略振转校正.从表1可以看出:这些方法对17O屏蔽常数的计算误差明显大于对13C屏蔽常数的计算误差，其MAD均在5×10-6以上，而这些方法对13C屏蔽常数的计算精度通常在2×10-6以下[9,13-14].FPA-M方法显著优于其他方法，CCSD(T)/pz3d2f次之，xOPBE和DSD-PBE86表现相当.注意到这些方法的MAX除FPA-M来自NNO外，其余都来自于F2O分子，这是由于F2O分子具有非常强的电子相关效应，精确的计算需要更高阶的相关效应来描述[12,29].

为更全面地研究FPA-M和xOPBE方法，将分子集扩展至图1所示的19个分子，计算结果见表2.同时也对比了MP2、结合不同基组的CCSD(T)方法以及常用的密度泛函，如M06-L、PBE0、OPBE和B3LYP的计算结果.图2给出了不同计算方法得到的17O化学屏蔽常数计算值相对于实验值的MAD，可以看出：对于19个小分子FPA-M仍然能给出最精确的预测，其MAD为5.2×10-6；与实验值相比，CCSD(T)方法呈现出良好的基组收敛性，随着基组的增大CCSD(T)方法的误差逐渐降低.这和本课题组前期的研究结果一致，即对于周期表前两周期的元素FPA-M的计算精度接近于CCSD(T)/CBS的极限[8-9].MP2方法和常用的DFT方法显然不能给出令人满意的结果，其计算的17O化学屏蔽常数MAD均大于21×10-6.有趣的是通过引入HF交换，xOPBE显著地改进了OPBE对17O化学屏蔽常数的描述，其MAD从21.7×10-6降低至8.2×10-6，表现甚至优于CCSD(T)/VQZ，接近于CCSD(T)/pz3d2f的精度.

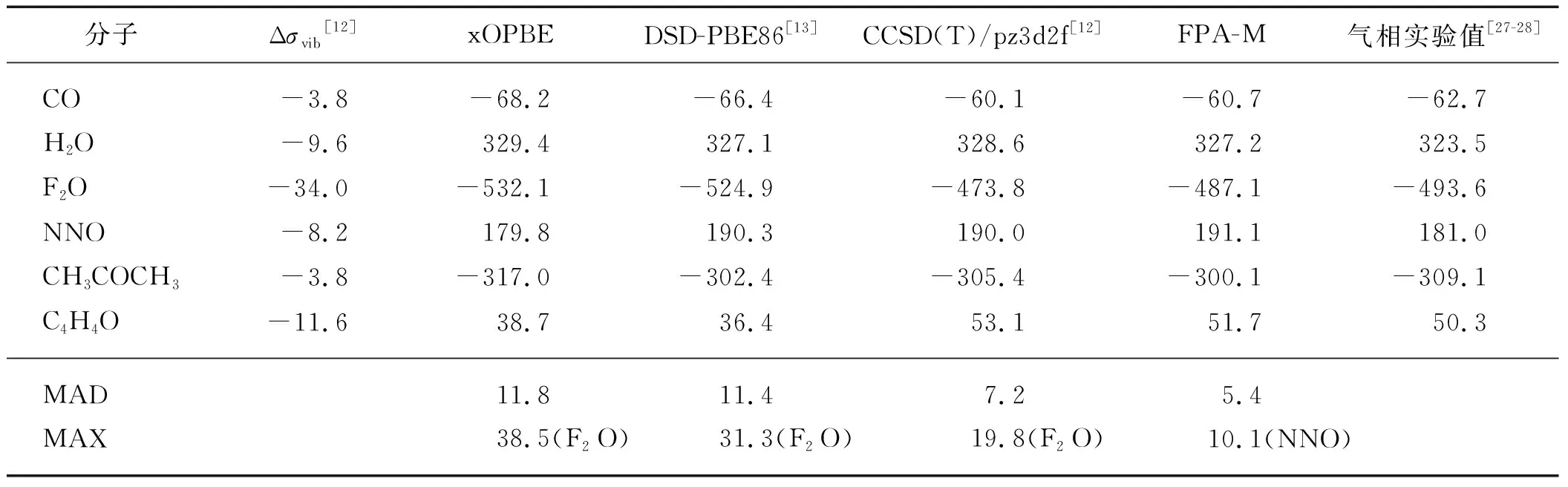
表1 采用不同理论计算方法得到的6个小分子的气相17O化学屏蔽常数Tab.1 The gas-phase 17O shielding constants of 6 molecules calculated with different theoretical calculation methods 10-6

表2 采用不同理论计算方法得到的19个小分子的气相17O化学屏蔽常数Tab.2 The gas-phase 17O shielding constants of 19 molecules calculated with different theoretical calculation methods 10-6

2.2 17O化学位移

化学位移因其可以反映原子核周围的电子环境而成为NMR波谱最重要的参数之一[30].与气相化学屏蔽常数相比，气相化学位移受振转校正的影响相对较小.这主要是因为振转校正通常是系统性的[12,31]，与参照物的差减可使误差相互抵消，从而提高化学位移的计算精度.

表3列出了19个小分子在不同理论计算方法下相对于CO的17O化学位移，及其相对于气相实验值的MAD.化学位移计算公式如下：

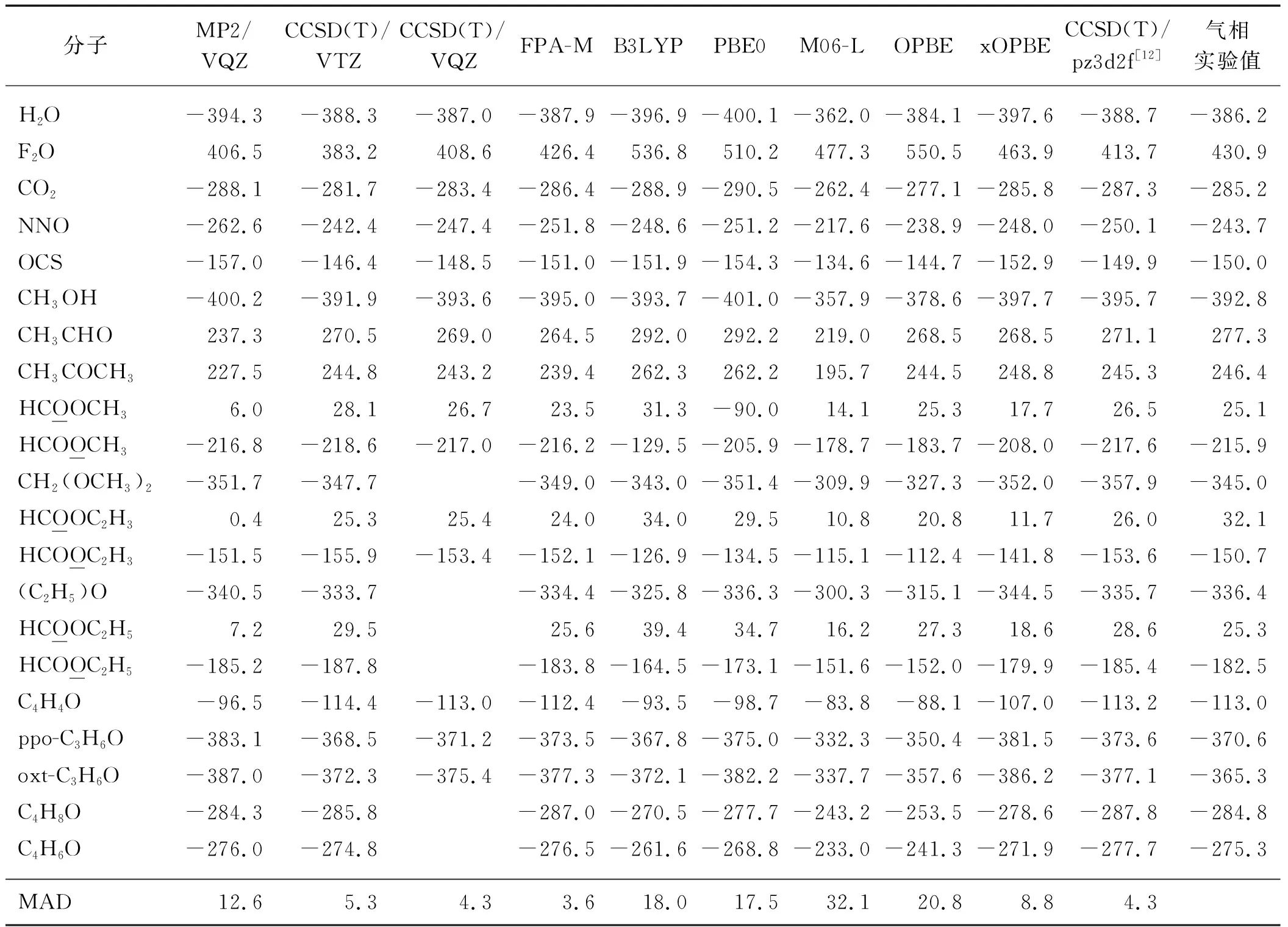
表3 采用不同理论计算方法得到的19个小分子的气相17O化学位移Tab.3 The gas-phase 17O chemical shifts of 19 molecules calculated with different theoretical calculation methods

δ=(σ(CO)-σ)×106,

(4)

其中σ(CO)为内标参照物CO的化学屏蔽常数，σ和δ分别为被测化合物的化学屏蔽常数和化学位移.

如表3所示，基于波函数的方法(FPA-M、CCSD(T)和MP2)对化学位移的预测精度明显高于化学屏蔽常数，而基于DFT的方法则取决于所采用的泛函.在化学位移的预测中FPA-M仍表现最佳，与实验值相比其MAD低至3.6，其中MAX来自CH3CHO分子(12.8).系统性误差的相互抵消也使得CCSD(T)方法表现非常优异，pz3d2f、VQZ和VTZ的MAD分别为4.3，4.3和5.3.值得一提的是，尽管MP2/VQZ不能给出精确的化学屏蔽常数，但其对化学位移的预测也明显优于常用的DFT方法，如B3LYP、PBE0、OPBE和M06-L.在所有的DFT方法中，xOPBE的表现最佳，其MAD为8.8，显著优于其他泛函，接近于大基组下CCSD(T)方法的精度.因此，对于大分子体系17O化学位移的计算，推荐使用xOPBE泛函.

3 结 论

本文系统地研究了不同计算方法在19个化合物的17O 化学屏蔽常数与化学位移计算中的表现.结果表明：对于化学屏蔽常数和化学位移，FPA-M方法均给出了最佳的表现，其精度显著高于结合大基组的CCSD(T)/pz3d2f方法；因此对于小于15个重原子的小分子体系，推荐使用FPA-M方法.此外，尽管xOPBE的参数优化仅针对13C化学位移，对于17O化学屏蔽常数与化学位移的预测xOPBE仍能给出足够精确的结果，其精度远高于常用的密度泛函，如B3LYP、PBE0、OPBE和M06-L，与DSD-PBE86双杂化泛函相当，接近于CCSD(T)/pz3d2f的计算精度；由于FPA-M仅适用于不超过15个重原子的体系，所以对于化学位移的常规计算，无论是13C还是17O，都推荐使用xOPBE泛函.