面向公平分配的资源分配模型设计与实现

陈奕冲，陈威仰

（1.东莞理工学院网络与空间安全学院，东莞 523820；2.广州华商学院数据科学学院，广州 511300）

0 引言

资源公平分配问题是指把有限的资源合理地分配到多个目标群体中，目前世界各地之间资源分布极不均衡，其包括自然资源，医疗资源等，其中发达国家普遍占据较多的资源。应尽量避免分配资源时资源分配不均而导致的资源争夺问题，资源争夺关系着世界政治格局，它们的持续安全供给关系着国计民生和国家安全，因此资源的公平分配显得格外的重要。

1 研究现状

现有资源公平分配方法主要有两种，一种是根据最大最小公平原则，在目标函数中表现为效用最小者利益最大，如最小满意度最大、最大设施负荷最小等，但这种方法对效率的损失比较大；二是通过效率和公平测度指标构建多目标模型，测度指标的选择和目标的权重等对公平结果的影响较大，计算也较为复杂。对于资源的公平分配问题，研究成果还比较少，对此本文提出了一个基于综合评价法的资源公平分配模型，采用的公平定义是基于结果平等思想，类同于经济学中的定义，即要求各成员之间的资源差距不能过大，并通过假设待分配资源与各国资源数据对提出的模型进行验证。

2 资源公平分配模型

2.1 模型假设

为了构建公平分配模型做出如下假设：①任何社会组织中存在不公平现象；②对已有的资源再不进行收回，只对待分配的资源进行新的分配；③现有的不公平现象同已有的分配方式有关系，并可以通过更正分配方式来实现公平；④实验论证中待分配资源为假设参数。

2.2 模型构建

在本模型中设有个国家，分别为,,,…,A，每个国家的人口数量不相同，将人口数量记为，则个国家对应的人口数量分别为,,,…,P，将各个国家现有资源记为，则各国对应的资源数量为,,,…,E，则对公平的定义有：

为常数。

个国家的人口总数为：

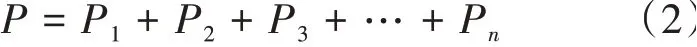
假设现要将数量为的资源全部分配给这个国家，每个国家所分配到的资源数量分别，，，…，E，对于总资源则有：

在理想的状态下，结合公式（1）（2）（3），对所有国家进行资源的公平分配，分配后的情况应该如公式（4）所示：

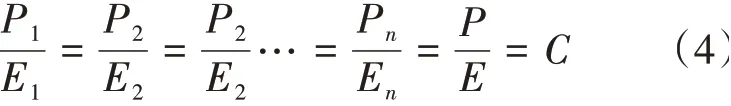
但在现实情况下，公平分配的过程中往往存在一定的不公平现象，这也意味着公平分配很难达到理想状态。所以，本文的目标是尽可能提高公平分配的程度，以使分配方法能够达到最大程度的相对公平。

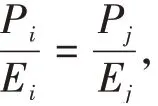
对于不同的国家之间，相同的值含义有所不同。当值不同但值相同时，此时两种情况的值都一样。但明显值大的情况中资源分配比值小的情况要更公平一些。因此，为了避免这类情况的发生，在绝对不公平度的基础上需要定义一个相对不公平度。对于不同国家和，他们的之间的相对不公平度如公式（6）所示。

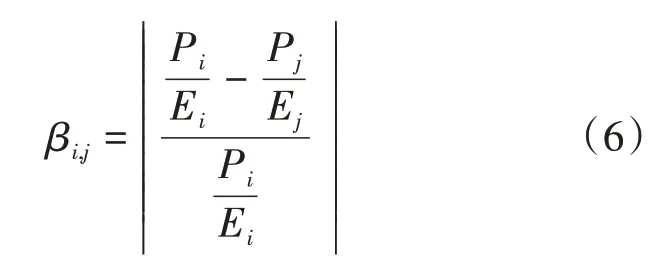
β表示国家相对于国家的不公平值。

假设现有待分配资源Δ，计划分配给国家和国家，两个国家原有的资源分别为和，且两个国家的资源总和为，具体分配方案如表1所示。

表1 资源分配方案

对于个国家的情况，达到公平时有：

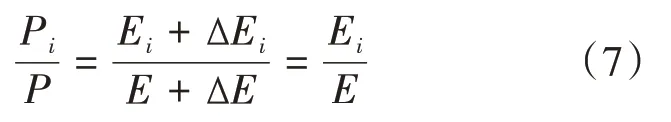
其中为已经分配和待分配的总资源之和，E+ΔE是国家已经分配资源和新分配的资源之和。

可以看出，总体资源的分配比重应该与人员结构相符，显然这种分配模式并不符合“按劳分配”的基本原则。为了能够体现按劳分配思想，需要在此模型上赋予人数以权重，并通过世界人口总数量、各国人口数量P、世界GDP总水平、各国的GDP水平G，结合公式（6）计算不公平值权重因子，并将权重因子作为资源分配的决策因素之一。的计算方式如公式（8）所示。

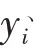
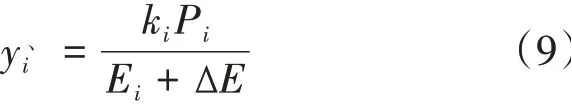
对于资源分配算法，根据、值的不同存在以下两种分配方式，如表2所示。

表2 加权后的分配情况

结合上述公式得出下列资源分配模型算法：

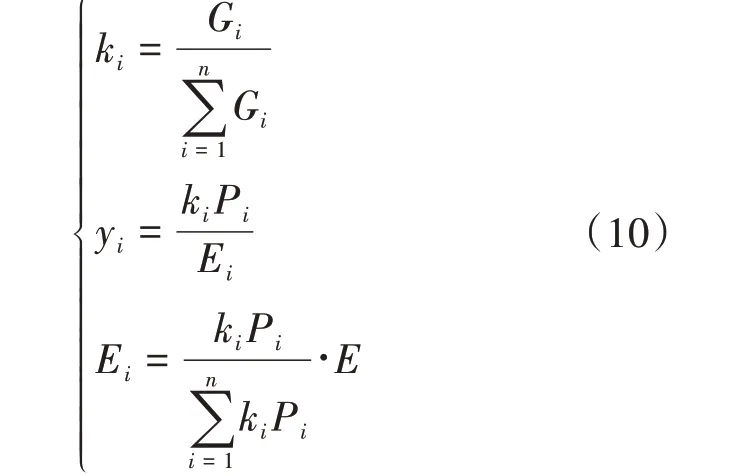
整个资源分配流程如图1所示。

图1 资源分配流程图

2.3 模型实现

本模型的核心Python代码伪代码如下：

3 实验与结果分析

3.1 实验数据

世界银行是联合国的一个专门机构，该机构下属的世界银行公开数据库是世界上最为权威的数据库之一，该数据库收录了世界各国超过7000个指标的数据，本次实验使用世界银行数据库公开的世界各国国民生产总值数据、世界各国人口数据、世界各国人均石油资源数据，采用数据抽样方法，选取了日本、德国、加拿大、法国、荷兰五个具有代表性的国家作为待分配对象国，利用Python对收集到的数据进行数据清洗，筛选出本文所需要的数据，提取后数据格式如表3所示。

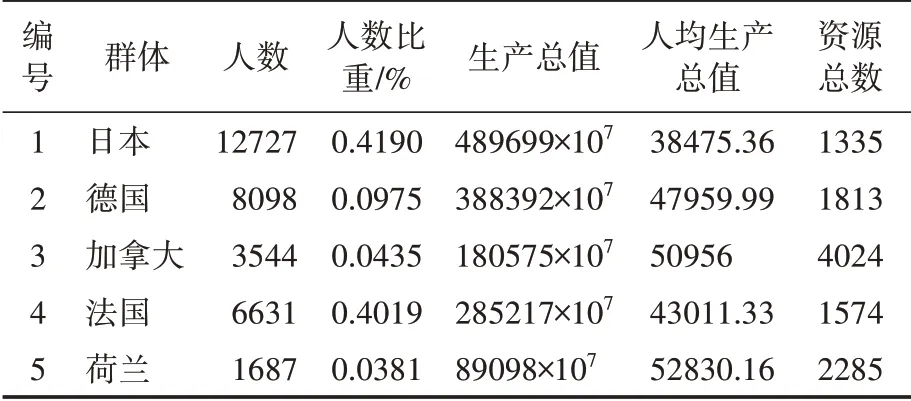
表3 各国数据

3.2 实验结果

模型验证假设有新增待分配的12000单位资源，将其记为Δ，即Δ=12000。根据模型，本文五个样本国家的国民生产总值及占比如图2所示。

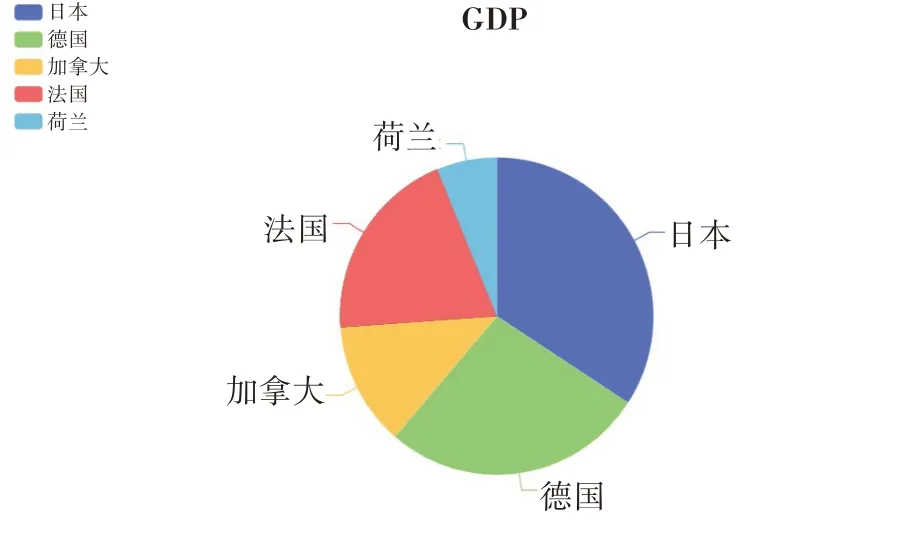
图2 各国生产总值

对得到的各国国民生产总值的占比进行归一化处理，计算得出各国的值，利用公式（8）计算得出各国的值如表4所示。

表4 各国权重

利用权重值，根据表3的数据，利用公式（10）求得各国国家的值，并根据值对表3从大到小进行重新排序，结果如表5所示。

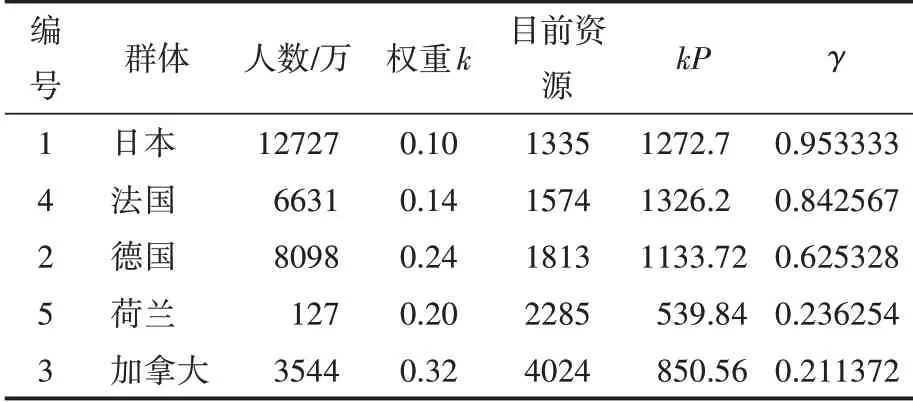
表5 分配前各国数据

此时待分配的12000单位资源，由于日本的值最大，根据模型分配规则，首先将资源对日本进行分配，根据公式（9）计算得到法国分配到全部资源后的值为0.6936，大于荷兰和加拿大的值，小于德国的值，为模型中的第三种情况，因此新增的资源应该在法国、日本还有德国之中进行分配，利用公式（10）计算的分配结果如表6所示。

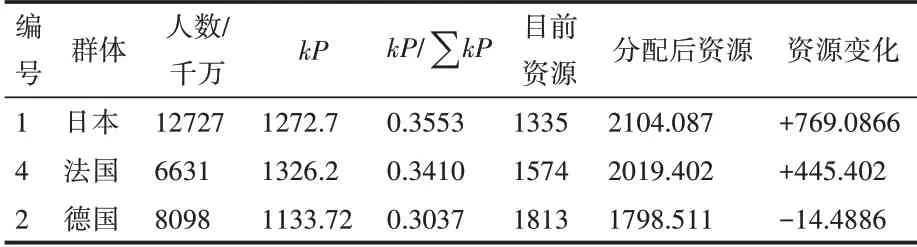
表6 各国分配数据

待分配资源在法国、日本还有德国之中公平分配后，得到各国的新资源数量。此时，若要达到结果公平，需要对德国减少资源分配。但根据本文的假设，模型只对资源进行新增分配而不对已有的资源进行回收，于是可得新增资源不需要分配给德国，只需要在法国和日本之间进行分配即可，于是根据公式（10）计算可得分配结果，其结果如表7所示。

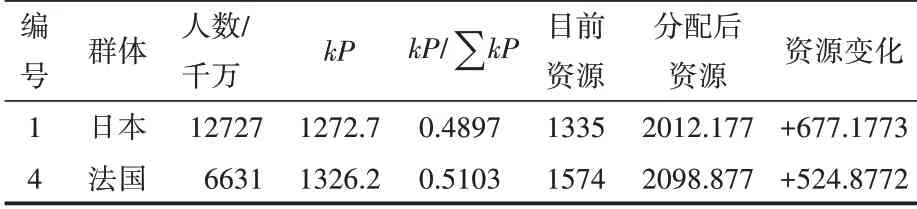
表7 各国分配数据

因此本次分配只有日本和法国可以分配到资源，其余各国无需分配资源，新增资源分配后的目前资源和值情况如表8所示。

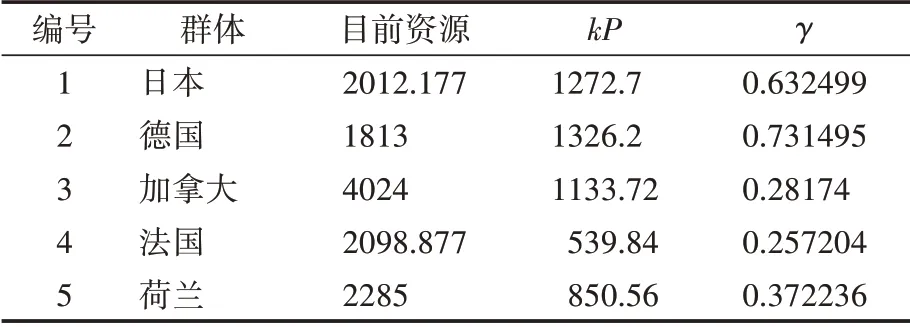
表8 分配后数据对比

3.3 实验分析

由资源分配后得到的关于法国和日本的数据，即表8中的数据可得法国和日本的不公平度的主要影响因子相比于资源分配之前即表5中的数据有减小，根据模型定义，决定因子减小意味着不公平度下降，从而得出通过此次的资源分配使得法国和日本相对于其他各国得到总的资源数更加公平，因此利用该模型进行资源公平分配是可行的。

4 结语

本文提出了面向公平分配的资源分配模型，结合计算机编程技术对资源的分配方式进行了初步的探索。通过分配前后的资源分配对象的绝对不公平因子减少，得出本模型可以进行资源公平分配的结论。当然，本模型中对于人口权重只考虑了各国国民生产总值这一单一因素，在实际的资源配置中需要考虑的因素更多，需要利用更多的因素来计算人数权重，从而得出更为精确的资源分配结果。