煤岩组合体的能量演化规律及差能失稳模型

左建平，宋洪强

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.中国矿业大学(北京)煤炭资源与安全开采国家重点实验室，北京 100083)

长期以来，煤炭为我国的经济发展提供了长足动力。未来一段时期煤炭作为我国主导能源的地位仍不会动摇。随着对煤炭资源需求的不断增加，浅部资源已日益枯竭，深部煤炭资源开采将趋于常态，但面临着诸多挑战，如冲击地压、煤与瓦斯突出、冒顶和突水等灾害。冲击地压灾害给人民生命和财产安全造成了严重损失，且随着开采深度与强度的增大，其发生的频率和烈度不断加强。一些研究表明，深部开采环境下，受高地应力影响，很多冲击地压灾害本质上是受强开采扰动下“岩体-煤体”组合结构整体失稳的结果。

关于煤岩组合模型的力学特性已开展了广泛研究。左建平等对煤岩组合体进行了一系列的单三轴及循环加卸载试验，研究了煤岩组合体的破坏模式、强度特性、声发射演化规律以及非线性破坏模型，并与煤岩单体试样进行了对比分析。HUANG等、陈绍杰等分别研究了加载速率、煤岩高度比对煤岩组合试样力学特性的影响。此外，杨磊等、陈光波等从能量角度研究了煤岩组合体的储能特性，认为煤岩组合系统中软弱的煤体是主要的能量积聚体。在煤岩组合模型的冲击倾向性方面也进行了一些研究。李纪青等开展了大量煤岩组合模型的冲击倾向性试验，表明煤岩组合模型测得的冲击倾向性指标均高于单一煤模型，建议采用组合模型来评价煤岩冲击倾向性。刘波等、陆菜平等、宋录生等、左建平等分别研究了不同类型煤岩组合试样的冲击倾向性，表明随着岩煤高度比、顶底板强度、煤样强度、均质性的增大，组合试样的冲击倾向性增强。

目前在冲击地压机理研究方面，国内学者提出了变形系统失稳理论、“三因素”理论、冲击启动理论、扰动响应失稳理论等。而对煤岩体冲击倾向性评价在冲击地压致灾机理研究中占有重要地位。

目前对煤岩组合模型冲击倾向性评价多是借鉴了煤的冲击倾向性指标。虽然2019年我国颁布的国标《冲击地压测定、监测与防治方法 第3部分：煤岩组合试件冲击倾向性分类及指数的测定方法》推荐使用剩余能指数测定煤岩组合模型的冲击倾向性，但该指标也是将整个组合试样视为单体来考虑。由于煤岩组合模型可以反映围岩性质对煤岩体冲击失稳的影响，因此，评判组合模型冲击倾向性的指标应考虑到煤、岩力学特性的差异。但这方面的研究目前还较少，牟宗龙等、TAN等分别提出了考虑顶底板积聚能量与煤体消耗能量关系的煤岩组合模型冲击倾向性指标。为此，笔者在分析了不同类型岩石能量积聚特性差异的基础上，研究了煤岩组合试样中煤体与岩体的弹性能密度演化规律，发现了峰值弹性能密度差与试样破坏程度的相关性。然后基于非平衡热力学和耗散结构的观点分析了煤岩组合系统的变形失稳过程，据此提出了一种新的评价煤岩组合模型冲击倾向性的指标。

1 不同类型煤岩能量积聚特性差异

每种岩石都具有不同的物理力学参数，如弹性模量、泊松比等，故一般情况下不同类型岩石也具有不同的能量积聚特性。笔者选取了6种典型岩石(煤)，其单轴加载下的应力-应变曲线如图1所示。表1列出了各岩石的弹性模量和单轴抗压强度。

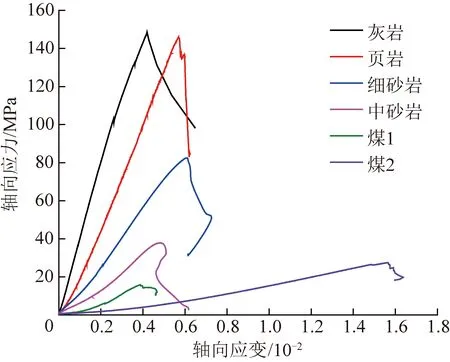
图1 不同类型岩石应力-应变曲线

表1 不同类型岩石的弹性模量与抗压强度

单轴压缩状态下单位体积岩石所积聚的弹性能可近似由式(1)计算：

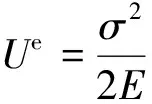
(1)

式中，为岩石某一应力水平下的弹性能密度；为轴向应力。

式(1)表明同一应力水平下岩石的弹性能密度主要取决于其弹性模量，且两者呈负相关性。分别选取煤1、煤2的抗压强度为2个应力水平，对不同类型岩石的弹性能密度进行对比分析，结果如图2所示。图2显示，某一应力水平下各岩石的弹性能密度随弹性模量的减小而单调递增；且岩石弹性模量越低，2个应力水平的弹性能密度相差越大，这表明岩石弹性模量越小，其积聚弹性能的能力对应力水平的变化更加敏感。

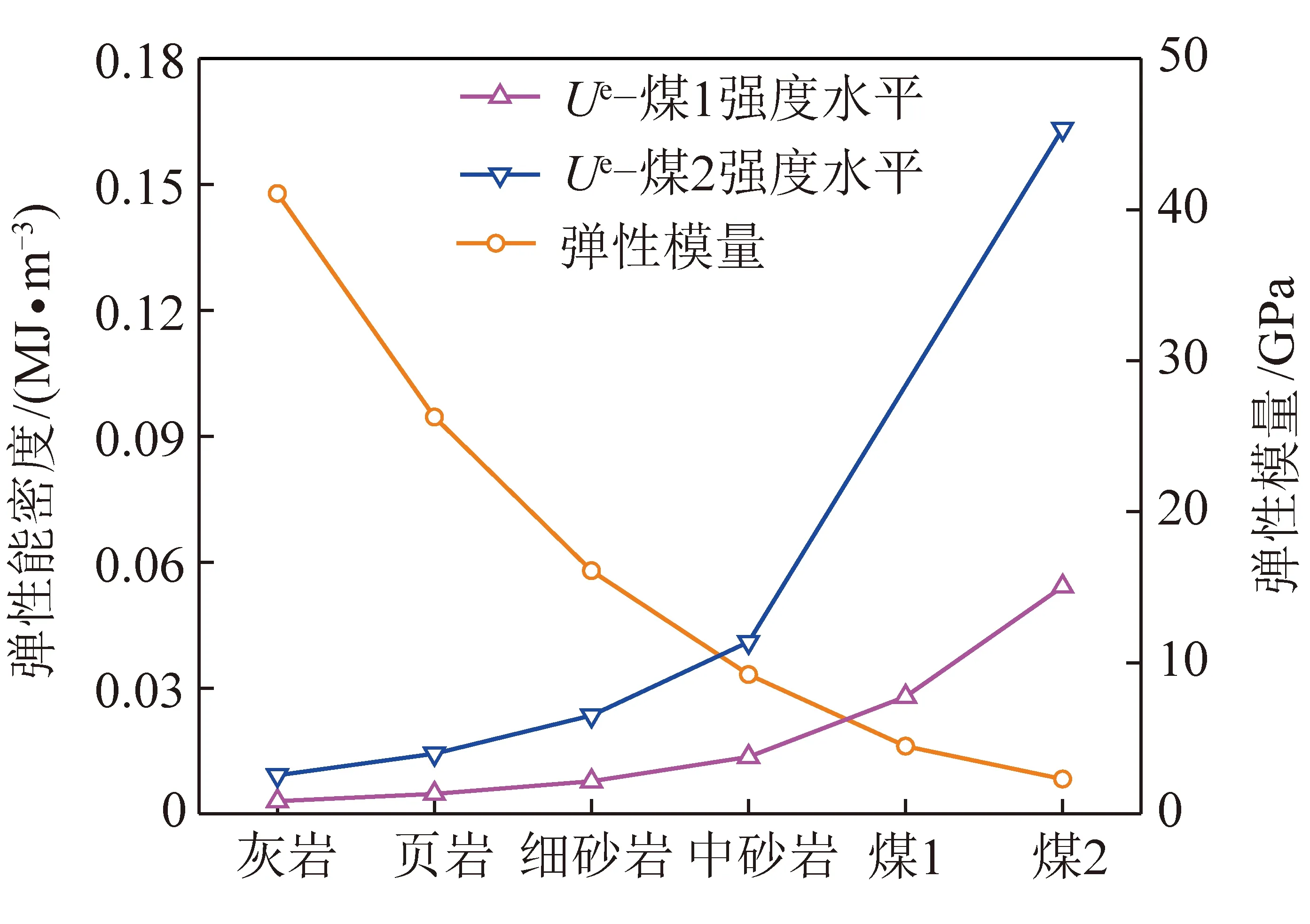
图2 不同类型岩石能量积聚特性

进一步对比分析同一应力水平时不同类型岩石与2种煤的弹性能密度差，仍分别取煤1、煤2抗压强度为2个应力水平，分别计算这2个应力水平下煤与各类岩石的弹性能密度差，如图3所示，同时也展示了各类岩石与2种煤的弹性模量比关系。由图3可知，与煤1对比，随岩煤弹性模量比降低，煤岩弹性能密度差也逐渐减小；与煤2对比，煤岩弹性能密度差也表现为随岩煤弹性模量比降低而减小，但减小幅度要大于前者，这与2种情况下岩煤弹性模量比的降低幅度相关。上述分析表明同一应力水平下，岩煤弹性模量比在一定范围内越大，相应的煤岩弹性能密度差就越大。

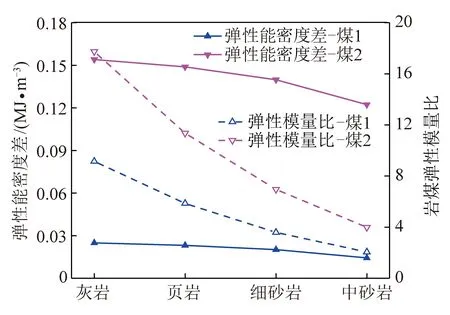
图3 不同类型岩石与煤的弹性能密度差

2 煤岩组合体弹性能密度差演化规律

2.1 煤岩组合试样弹性能积聚特性

煤岩组合试样作为一种特殊的结构体，本质为不同类型岩石的叠合，加载过程中各分层仍保持各自特有的能量积聚特性。为对比煤岩组合试样中各分层岩石的能量积聚特性，开展了砂岩-煤组合试样的单轴压缩试验，通过分别在岩体、煤体表面黏贴应变片的方式得到各自的变形行为，其中岩体与煤体均设置了4个水平应变片和2个竖向应变片，应变片粘贴位置及具体的试验过程参考文献[26]。图4为SG1，SG2等2个煤岩组合试样中各分层的应力-应变曲线，其中SG1-R和SG2-R表示组合试样中的岩体，SG1-C和SG2-C表示组合试样中的煤体。从图5可看出，组合试样中岩体与煤体的变形特性明显不同。

图4 煤岩组合试样中各分层岩石应力-应变曲线

根据上述试验结果，由式(1)可得到组合试样中各分层的弹性能密度演化规律，如图5所示。由图5可看出，在加载初期，组合试样中煤体与岩体的弹性能密度均增长比较缓慢。随着加载进行，两者的弹性能密度增长速率逐渐加快，且煤体的增长速率大于岩体，导致2者的弹性能密度差越来越大，这表明组合试样中弹性模量较小的煤体是能量积聚主体。文献[12-13]也得出了类似的结论。

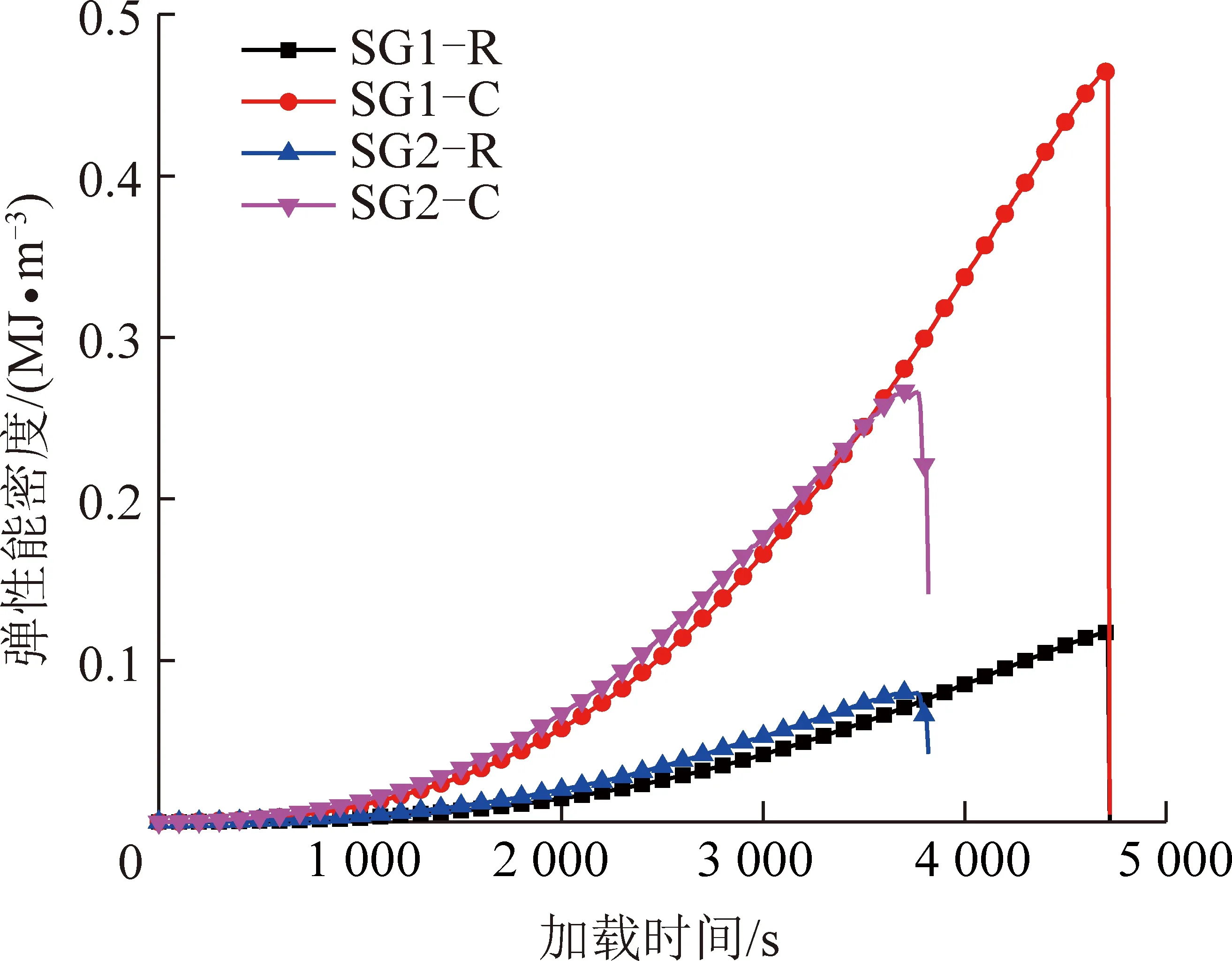
图5 煤岩组合试样中各分层岩石弹性能密度演化规律

同一应力水平下组合试样中煤体与岩体弹性能密度差Δ可由式(2)定义，利用该式可分析组合试样中煤体与岩体积聚弹性能的差异程度。

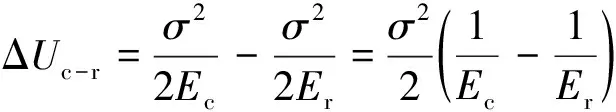
(2)

式中，,分别为组合试样中煤体、岩体的弹性模量。

图6给出了2个煤岩组合试样煤岩弹性能密度差的演化规律及对应的最终破坏形态。从图6可明显看出，加载初期2个组合试样的煤岩弹性能密度差几乎为0；随着加载进行，其增长速率逐渐加快，并在峰值强度处达到最大值，然后迅速跌落。对比2个组合试样发现，SG1试样弹性能密度差的最大值远大于SG2试样，同时前者弹性能密度差在峰后的减小速率快于后者。对比2者的破坏形态可知，SG1试样发生了整体粉碎性冲击破坏，并伴随响亮的爆裂声，而SG2试样发生了煤岩交界面附近的局部破坏，破坏时发出清脆的破裂声。由图5可知，之所以SG1试样的峰值弹性能密度差远大于试样SG2，主要是因前者煤体的峰值弹性能密度远大于后者，而前者岩体的峰值弹性能密度仅稍大于后者。由于煤体是组合试样中弹性能积聚主体，同时也是破坏主体，因此当达到峰值强度后，SG1试样因可释放的能量远大于试样SG2，故前者产生的破坏明显比后者严重。上述分析表明，组合试样中煤岩峰值弹性能密度差与其最终的破坏形态以及破坏程度具有明显关联，即峰值弹性能密度差越大，往往试样破坏越剧烈。

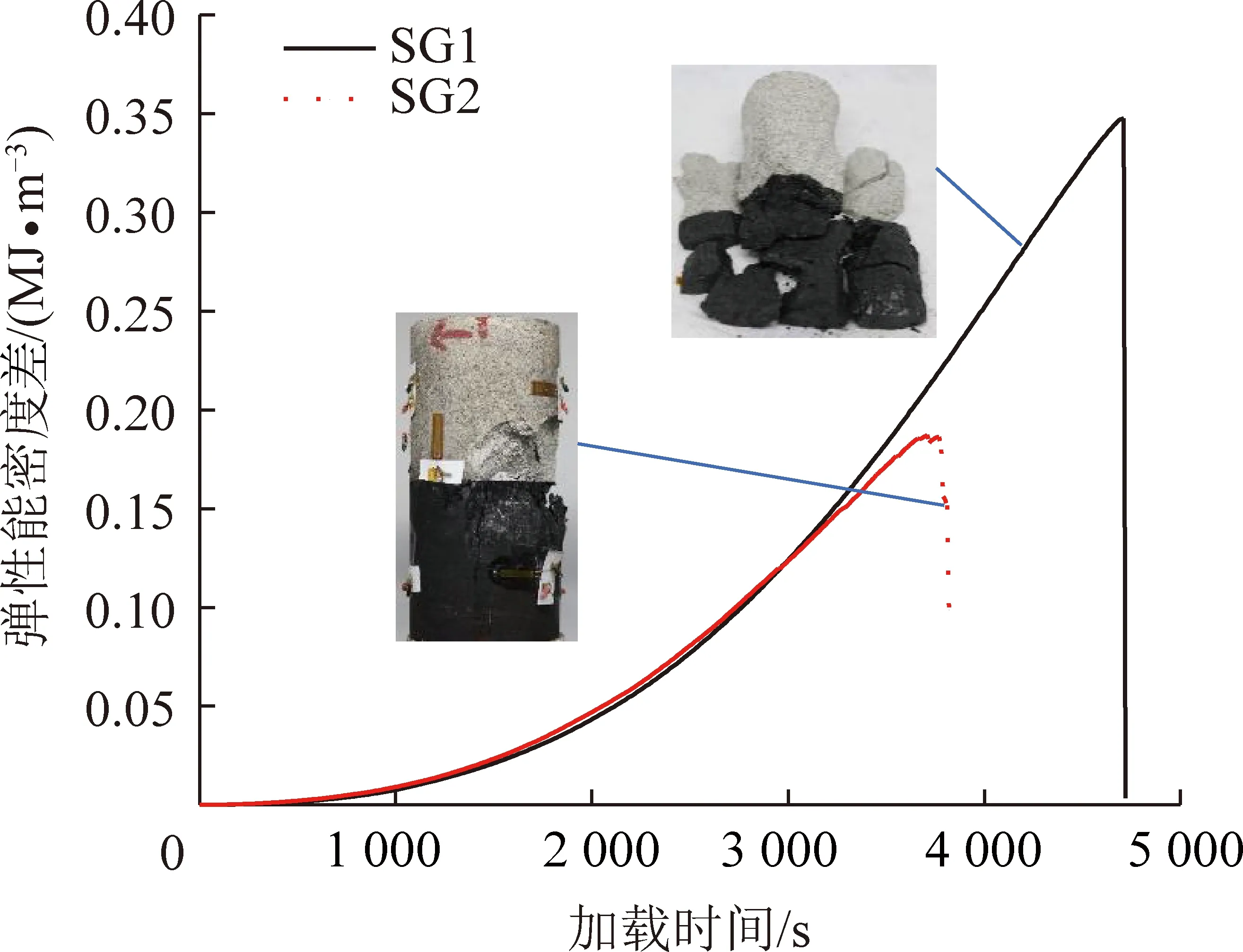
图6 组合试样中煤岩弹性能密度差演化规律

2.2 不同类型煤岩组合试样峰值弹性能密度差影响因素分析

基于2.1节的分析，笔者通过大量检索煤岩组合试样相关文献中的试验结果来进一步验证试样的峰值弹性能密度差与其破坏程度的关系，并讨论了影响峰值弹性能密度差的因素。需要说明的是，对于大多数常规试验研究，受到试验条件限制，或为实现不同的试验目的，有时无法得到各分层岩石的变形特性，从而不能直接获得各分层实际的弹性模量。本节中计算组合试样中煤体与岩体弹性能密度时统一采用其标准试样的弹性模量。

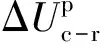
图7展示了表2中有记录的试样冲击能指数与相应的峰值弹性能密度差的关系。从图7可看出，两者的关系整体上并不明显，这主要与试样自身的离散性、加载条件的差异性以及人为处理数据的主观性等因素有关。尽管受上述诸多因素的影响，对于红色虚线间的数据，2者大致呈正相关性，即峰值弹性能密度差越大，冲击能指数也越高。另外由文献[15,17]可知，煤岩组合试样的峰值弹性能密度差越大，相应的弹性能指数也越大，而动态破坏时间具有减小的趋势。一般而言，试样的冲击能指数、弹性能指数越大，动态破坏时间越短，则代表其冲击倾向性越强。上述分析进一步表明组合试样的峰值弹性能密度差与其破坏的剧烈程度密切相关。

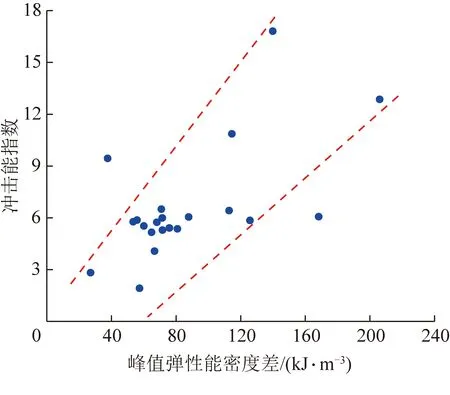
图7 冲击能指数与峰值弹性能密度差的关系

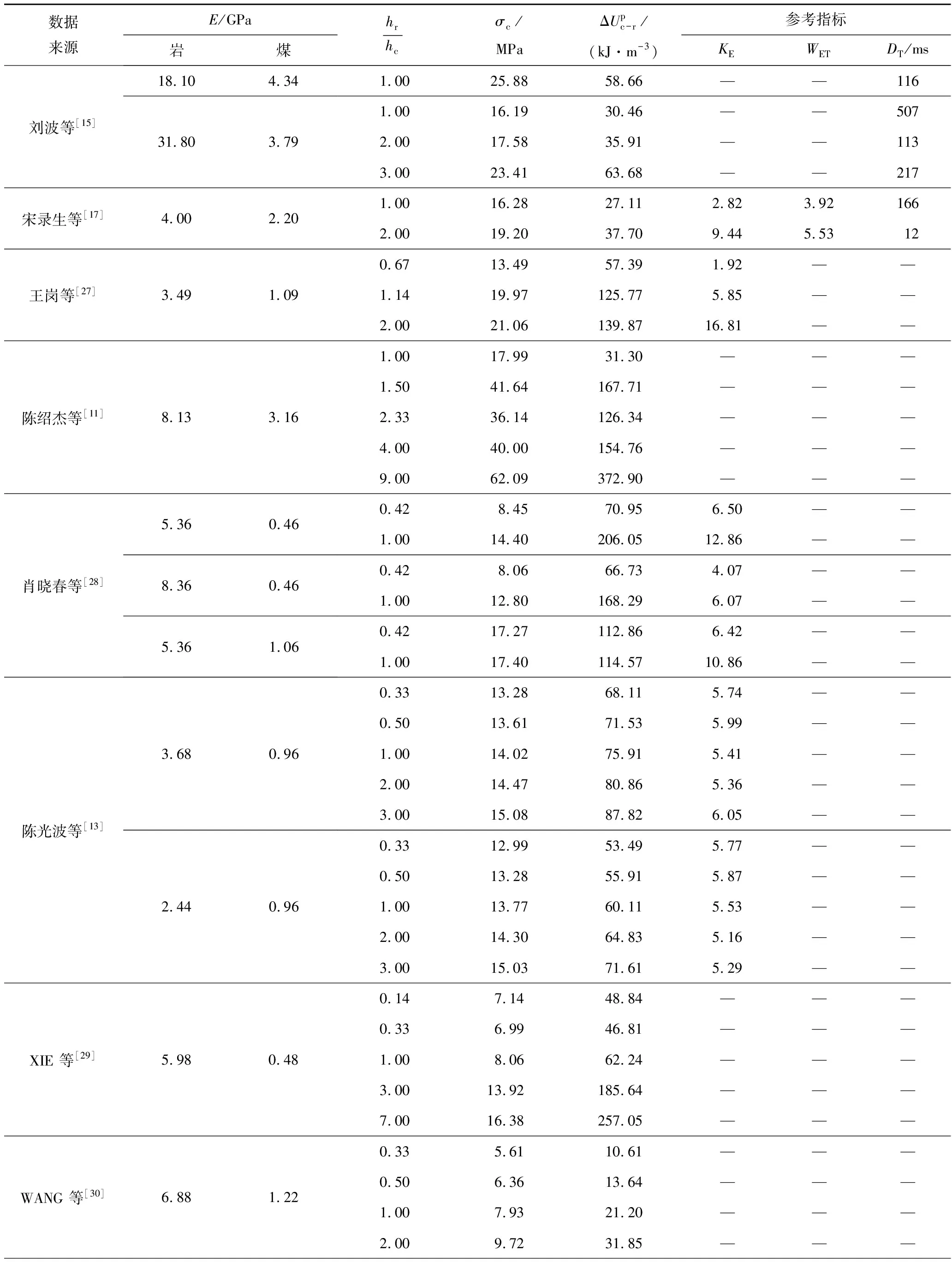
表2 不同类型煤岩组合试样峰值弹性能密度差

由表2知，组合试样的峰值弹性能密度差受到抗压强度、煤岩弹性模量以及高度比等多个因素影响，下面对每一因素进行具体分析。图8展示了峰值弹性能密度差与抗压强度的关系，其中相同颜色的数据点表示煤的弹性模量相同。图8(a)，(b)分别为岩煤高度比均为1和不同岩煤高度比下的试验结果，可以看出2种情况下表现出的规律一致，即同一种煤时，组合试样的峰值弹性能密度差随其抗压强度的增大而增大，且增长速率也逐渐增大；不同煤的情况时，该增长趋势以原点为中心，随煤体弹性模量增大(顺时针方向)而变缓。表明组合试样峰值弹性能密度差随抗压强度变化的增长趋势显著受到煤体弹性模量的影响，即煤体弹性模量越低，峰值弹性能密度差对抗压强度变化越敏感。

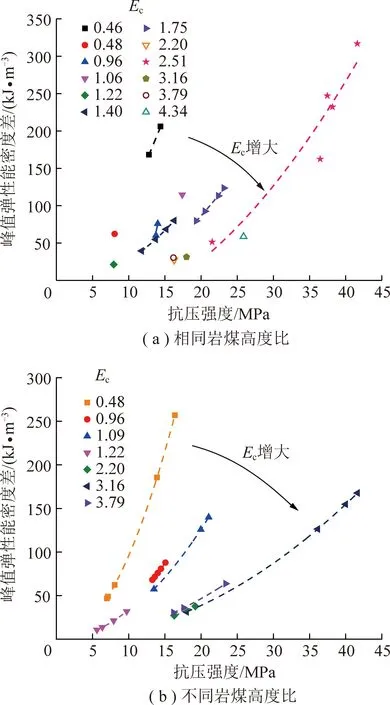
图8 峰值弹性能密度差与抗压强度关系

图9分析了不同影响因素下组合试样峰值弹性能密度差的变化规律，其中图9(a)～(c)均为岩煤高度比为1的试验结果，即保证了岩煤高度比这一因素相同。由图9(a)可看出，组合试样峰值弹性能密度差随煤体弹性模量增大的变化规律并不明显。一方面是由于试样本身的非均质性以及所分析的数据量较少；另一方面由图8分析可知，组合试样的峰值弹性能密度差显著受其抗压强度与煤体弹性模量的共同影响。由式(2)可知，煤体弹性模量呈反比例函数形式，而抗压强度呈二次函数形式，2项具有相反的变化趋势，故2项将对峰值弹性能密度差产生相反的影响。由图9(b)可看出，试样峰值弹性能密度差与岩体弹性模量的关系也不明显。这可能是由于所分析数据点的岩体弹性模量多集中在5～10 GPa，导致规律不明显。岩煤弹模比对组合试样峰值弹性能密度差的影响如图9(c)所示，虽然数据点也相对比较离散，但仍可看出两者之间基本呈正相关关系。图9(d)展示了岩煤高度比对峰值弹性能密度差的影响，其中相同颜色的数据点表示煤的弹性模量相同。可看出，同一种煤体情况下，随岩煤高度比增大，峰值弹性能密度差也逐渐增大；不同煤体情况时，峰值弹性能密度差的增长速率存在差异。由表2中的数据可知，岩煤弹模比和岩煤高度比增大均可提高组合试样的抗压强度，但前者对抗压强度增强的幅度有限，而后者能明显提高抗压强度。可见，岩煤弹模比和岩煤高度比主要是通过影响试样的抗压强度从而改变组合试样的峰值弹性能密度差。

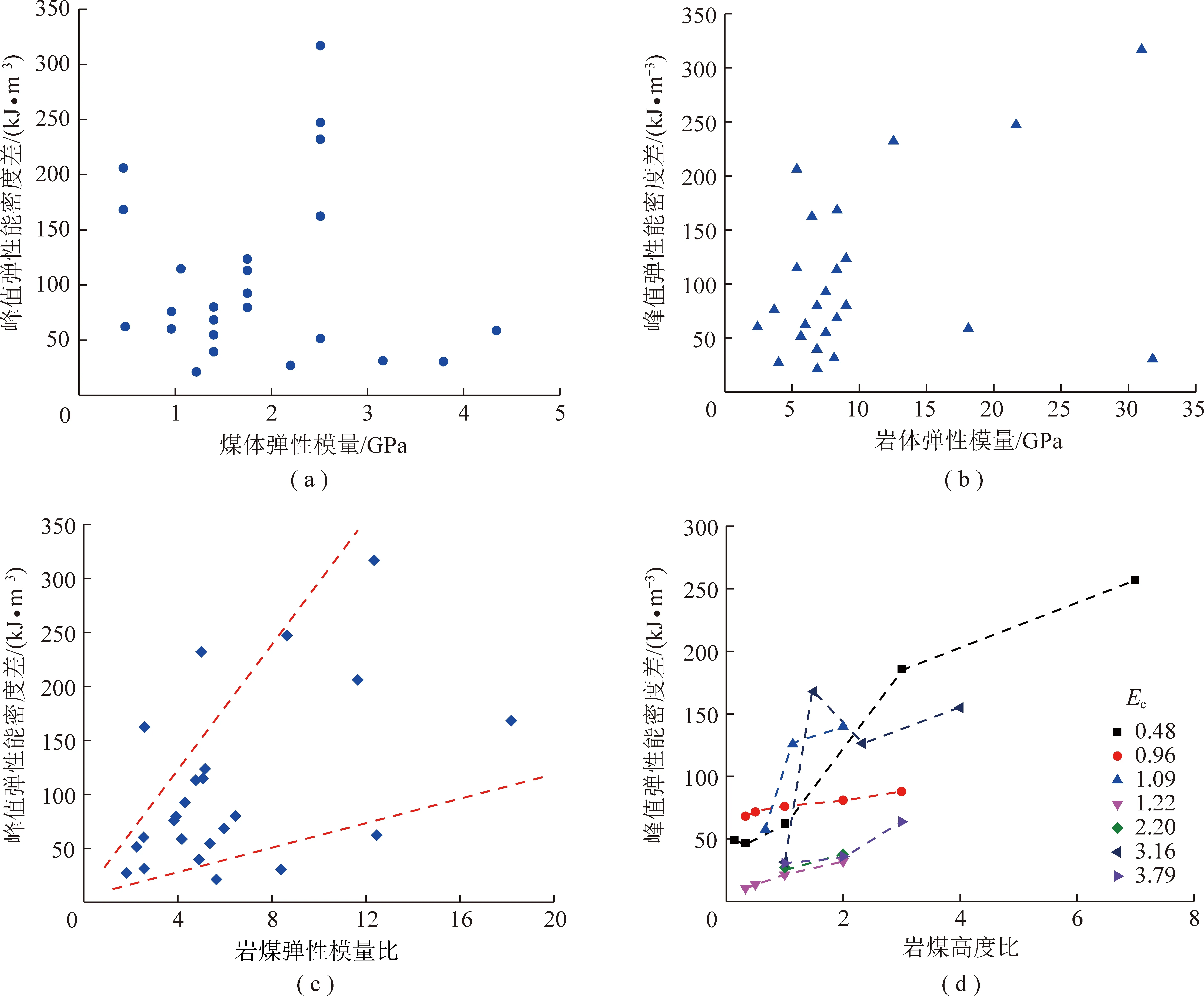
图9 不同影响因素下峰值弹性能密度差变化

由前文分析可知，抗压强度和煤体弹性模量对组合试样峰值弹性能密度差具有相反的影响。为进一步比较2者对峰值弹性能密度差的影响程度，搜集了100个标准煤样的试验数据进行分析。对于标准煤样，可将其视为与弹性模量无限大岩体(压头)的组合试样，从而可忽略岩体弹性模量、煤体厚度等对峰值弹性能密度差的影响。需要说明的是，此处将试验机压头视为弹性模量无限大岩体，其弹性能密度几乎为0，故煤样的峰值弹性能密度即煤样与压头组合的峰值弹性能密度差。图10(a)展示了100个标准煤样的抗压强度与其弹性模量的关系。由于所选的煤样取自多个矿区，即使同一矿区的煤样也会因煤的非均质性而存在差异，因此数据点相对比较离散。但可以看出两者之间呈正相关性。图10(b)展示了煤样峰值弹性能密度与其弹性模量的关系。可以看出，虽然数据点仍表现出相对高的离散性，但可以发现两者之间具有弱正相关性。

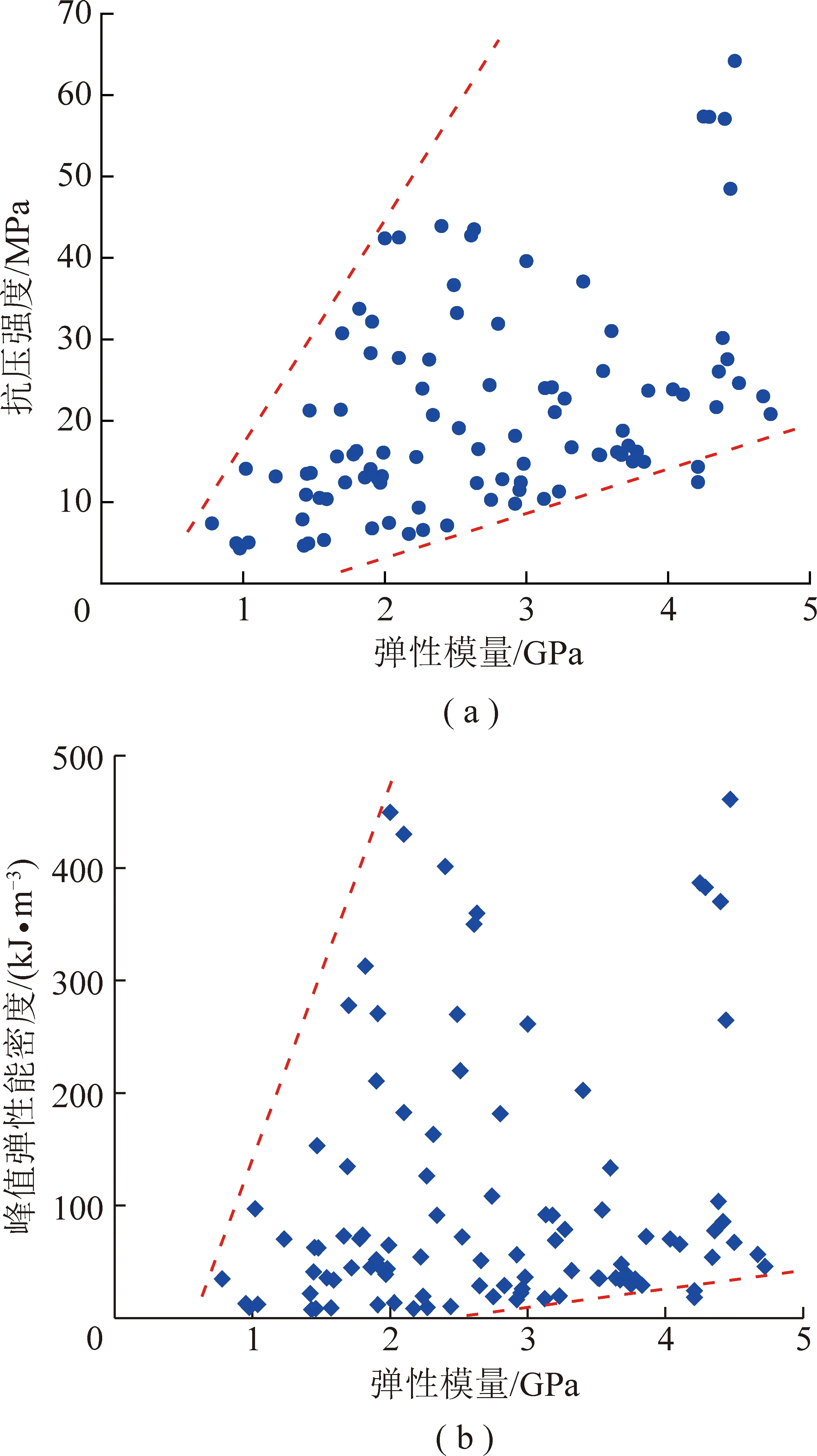
图10 煤样弹性模量与抗压强度、峰值弹性能密度关系

根据前文分析，随煤体弹性模量增大，式(2)中1/项逐渐减小；而随抗压强度增大，项却逐渐增大，故两者对峰值弹性能密度差具有相反的影响。由图10可知，煤体弹性模量与其抗压强度之间存在正相关关系，与峰值弹性能密度之间为弱正相关性，说明项对峰值弹性能密度差的影响大于1/项，即组合试样抗压强度对峰值弹性能密度差的影响程度要大于煤体弹性模量。

综上所述，煤岩组合试样的峰值弹性能密度差与抗压强度、煤体弹性模量、岩煤高度比、岩煤弹性模量比等因素均具有正相关关系，而与岩体弹性模量的关系不明确。岩煤高度比、岩煤弹性模量比主要是通过改变抗压强度从而影响峰值弹性能密度差。抗压强度是组合试样峰值弹性能密度差的主控因素。

3 煤岩组合体差能失稳分析

在非平衡态热力学研究中，PRIGOGINE把处于开放和远离平衡的条件下，与外界环境交换物质和能量的过程中通过能量耗散和内部非线性动力学机制形成和维持的宏观时空有序结构称为耗散结构。岩石的变形破坏是一种能量耗散的不可逆过程，因此煤岩组合体的变形失稳本质上也是产生时空有序结构的过程。

基于2.1节组合试样煤岩弹性能密度差演化规律，从弹性能差值的角度来分析煤岩组合体形成耗散结构的过程。图11构建了组合煤岩系统的差能失稳分析模型，其中煤岩系统的上部为岩体，下部为煤体，煤岩体内的绿色区域示意积聚弹性能的时空分布，红色爆炸图形表示弹性能的快速释放，黑色线条代表煤岩体内的宏观裂隙。未加载时，组合煤岩处于稳定的平衡态。加载初期，煤岩体内部微观结构开始发生变化，煤、岩体均积聚了少量弹性能，但2者大致相等，即弹性能密度差接近0，此状态可称为准稳定态。随着加载进行，煤、岩体积聚的弹性能不断增加，煤岩系统变得愈发不稳定，开始进入亚稳定阶段。在该阶段，伴随着微裂隙扩展等不可逆过程发生，产生了各种形式的能量耗散。随煤岩体内部结构的不断调整，微裂纹由随机分布逐渐向有序发展，开始形成宏观裂纹；应力由近似均匀分布开始在某些区域产生应力集中现象。同时，因煤体与岩体的固有力学特性存在差异，积聚的弹性能由近似相等地分布在煤体与岩体中逐渐主要分布在煤体中，导致2者的弹性能密度差逐渐增大，这是煤岩组合体变形破坏过程中有序化的一种特殊表现形式。可见煤岩系统正逐渐远离平衡。当达到组合煤岩的抗压强度时，煤体与岩体弹性能密度差也达到最大程度，此时煤岩系统处于最不稳定的临界状态。因为此后即使不主动卸载，由于裂纹的非稳定扩展也将导致煤岩系统的承载能力快速失效。这种突变是一种失稳现象，标志着煤岩系统进入失稳阶段。伴随着裂纹的快速扩展、贯通，积聚在煤岩体内的弹性能快速释放，如果具备足够的剩余能量，将为煤岩碎块的抛射提供一定动能。在失稳阶段，随着煤岩体内部弹性能的释放，煤体与岩体的弹性能密度差快速减小。当2者的弹性能密度差稳定在一个较低水平时，表明煤岩系统已进入一个新的稳定状态，该状态对应于某一宏观有序结构，即耗散结构，表现为变形局部化的出现或宏观裂纹沿某一方位汇聚成了大裂隙。

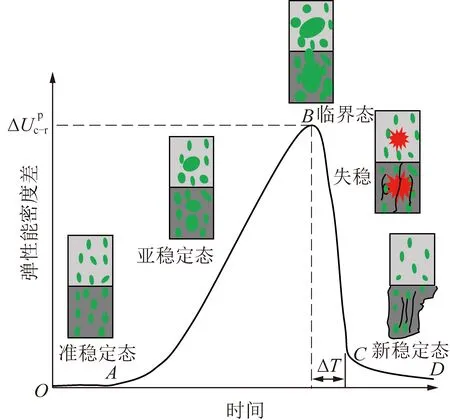
图11 组合煤岩系统差能失稳分析模型

由上述分析可知，当组合煤岩系统处于临界态时，煤体与岩体的弹性能密度差达到最大程度，此时系统处于最不稳定状态，任一微小的扰动都将导致系统发生突变。由岩石力学试验可知，岩石的峰后失稳一般有2种形式：渐进失稳和冲击失稳。渐进失稳发生时，系统由临界态需经历一定的时间才过渡到新稳定态；而发生冲击失稳时，煤岩系统则瞬间由临界态过渡到新稳定态。同时，由第2节可知，煤岩系统的峰值弹性能密度差越大，往往煤岩体越容易发生冲击失稳。

基于上述差能失稳分析模型，笔者提出以煤岩系统的峰值弹性能密度差与失稳阶段持续时间的比值作为评价煤岩组合体冲击倾向性的指标，即煤岩差能失稳指标，其物理意义为煤岩系统失稳阶段煤体与岩体弹性能密度差的变化率。该指标的表达式为

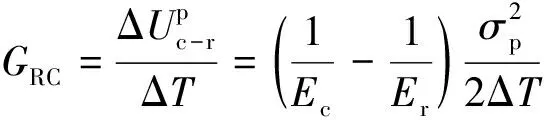
(3)

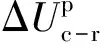
由第2节可知，上述指标考虑了抗压强度(应力水平)、煤岩弹性模量(材料特性)和岩煤弹模比、高度比(结构特征)等因素对煤岩系统失稳的影响，与冲击地压发生的“三因素”相比，此处可视为广义上的组合煤岩失稳“三因素”。另外，该指标通过峰值弹性能密度差以能量的形式将影响组合煤岩失稳的因素加以考虑，体现了煤岩体破坏是能量驱使的本质。同时，该指标还包含了煤岩体失稳阶段的持续时间，可体现能量释放的时间效应。多位学者指出煤岩的冲击倾向性应为能量与时间的双重函数，即与单位时间内弹性能的释放量相关。综上所述，采用煤岩差能失稳指标评价煤岩组合体的冲击倾向性具有一定可行性。

4 煤岩差能失稳指标合理性验证

本节拟通过室内试验数据和数值模拟试验结果来验证煤岩差能失稳指标的合理性。

首先选取了表2中有动态破坏时间记录的试验结果，此处可将动态破坏时间视为煤岩体失稳的持续时间，分析结果见表3。表3中前5个试样的冲击倾向性试验判定结果均为弱冲击，而试样6为强冲击。对比各试样的差能失稳指标可看出，前5个试样的均小于1，与试样6的存在量级上的差别，表明煤岩组合试样的越小，其冲击倾向性越弱。

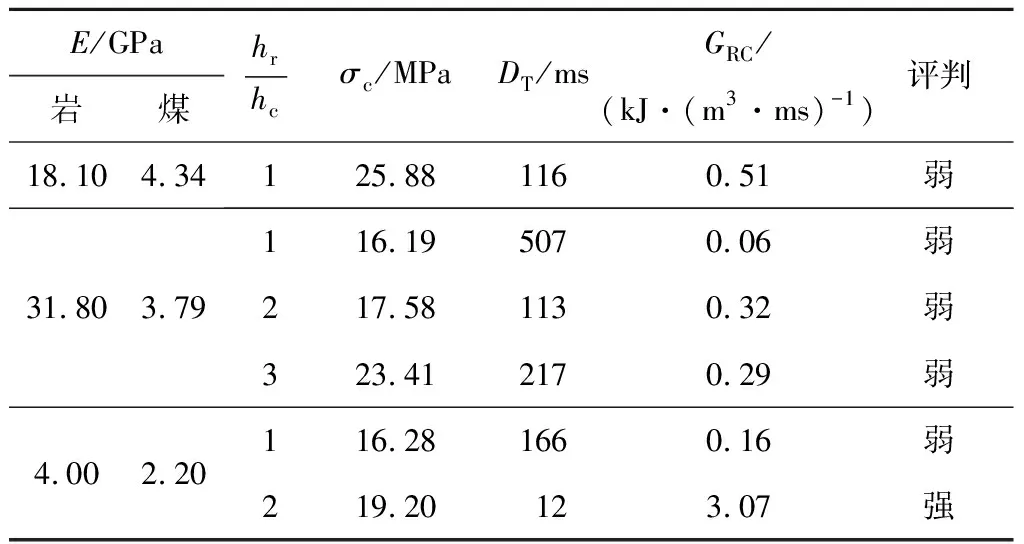
表3 煤岩组合试样冲击倾向性测定结果

根据文献[11-12,30]中煤岩组合试样的试验结果，采用PFC建立相应的数值模型来分析差能失稳指标随岩煤强度比、高度比的变化规律。为了更好地反映岩石类材料的力学性能，颗粒间的接触均采用平行黏结模型。首先建立了相应煤、岩样的数值模型，如图12(a)所示，模型尺寸均为长100 mm，宽50 mm。煤样颗粒半径为0.4～0.6 mm，岩样颗粒半径为0.4～0.7 mm，通过设定一定的孔隙率使颗粒在此范围内随机生成。通过细观参数的不断“试错”，使煤、岩样的模拟结果尽可能与相应的试验结果(抗压强度、弹性模量、泊松比)接近，最终确定煤、岩材料的细观参数见表4。在此基础上，采用表4中的细观参数开展不同组合条件下煤岩组合试样的数值模拟，其中岩煤高度比为1时的数值模型如图12(b)所示，各组合条件下的模拟结果见表5。

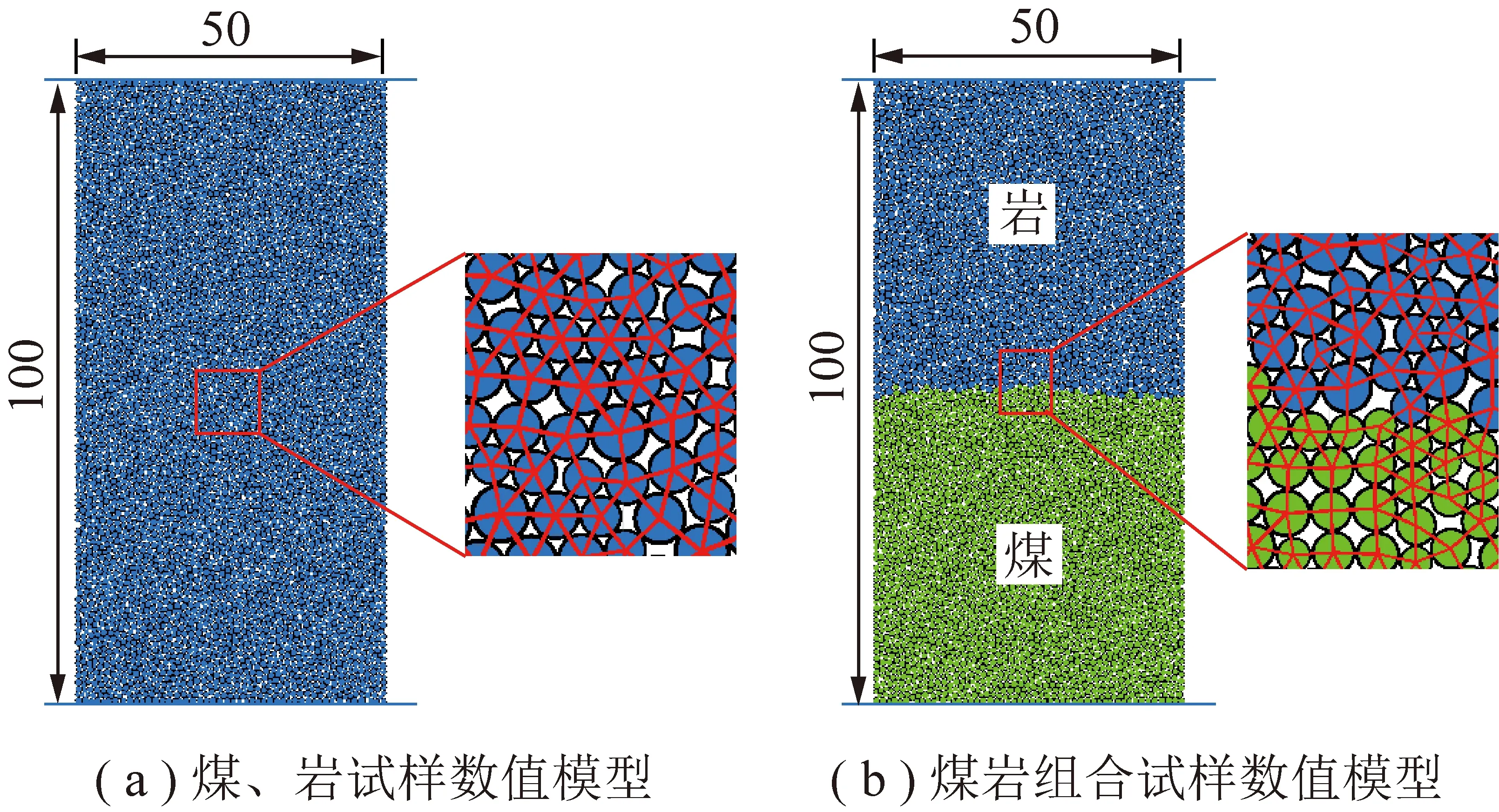
图12 PFC2D数值模型

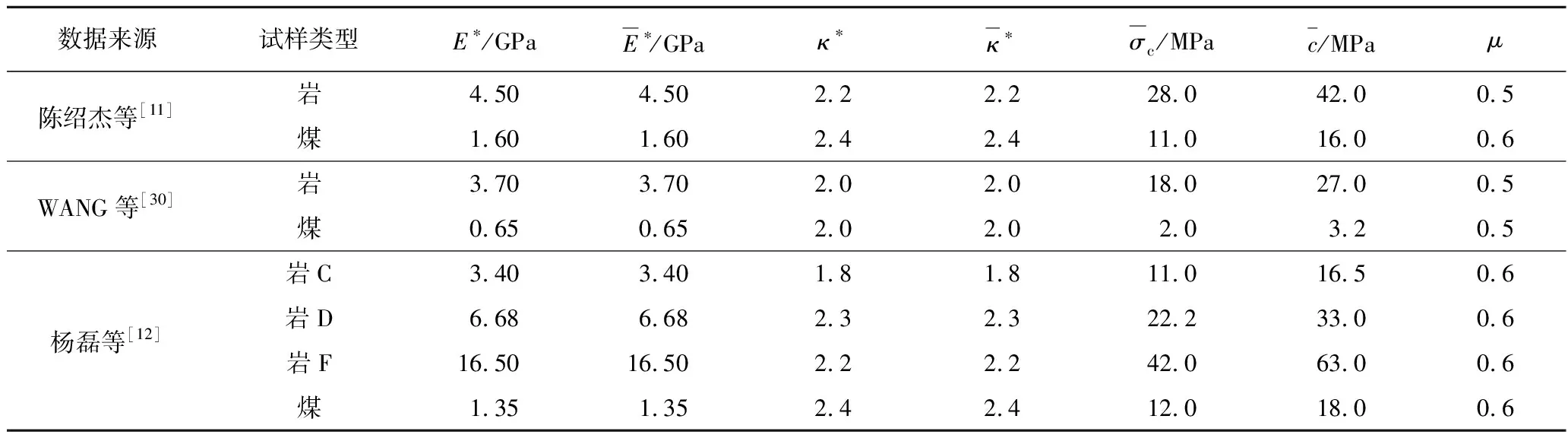
表4 煤岩材料细观参数

由表5可看出，试样1抗压强度的模拟结果为30.02 MPa，而试验值仅为17.99 MPa，2者相差较大。

因表5中前5组试样是研究高度比对差能失稳指标的影响，其他参数必须一致，所以前5组模型的细观参数设置是相同的。因真实试样的非均质性较强，故试样强度往往具有一定离散性。但总体来看，本节所建立的数值模型可较为准确地反映不同组合条件下煤岩组合试样的力学特性。

借鉴文献[40]采用试样破坏后的远场碎屑质量占比和平均粒径尺寸来表征试样破碎程度和冲击倾向性强弱的方法，笔者利用数值模拟中试样破坏之后煤体生成碎片的平均体积表征煤体的破碎程度，即碎片平均体积越小，表明煤体破碎越严重。同时，通过统计试样破坏后质心超出试样初始边界的煤碎片体积占煤碎片总体积的比值来衡量煤体的冲击剧烈程度，即超出边界的煤碎片体积占比越高，表明煤体发生冲击越剧烈。图13展示了不同组合条件下煤岩组合试样冲击破碎程度的变化规律。由图13(a)，(b)可看出，不论对高强度还是低强度的组合试样，随岩煤高度比增大，组合试样的和也逐渐增大，同时煤碎片的平均体积呈减小的趋势，均表明其冲击破坏程度随岩煤高度比的增大而加剧。由图13(c)可看出，随岩煤强度比增大，组合试样的峰值强度、超出边界的煤碎片体积占比以及煤碎片平均体积均表现出与图13(a)，(b)相同的变化趋势，表明在该岩煤强度比范围内，组合试样的冲击倾向性随岩煤强度比增大而有所提高。图14，15展示了不同组合条件下煤岩组合试样的破坏特征，其中红色虚线表示煤岩界面，可明显看出随岩煤高度比和强度比增大，组合试样中煤体的冲击破碎程度愈发严重。

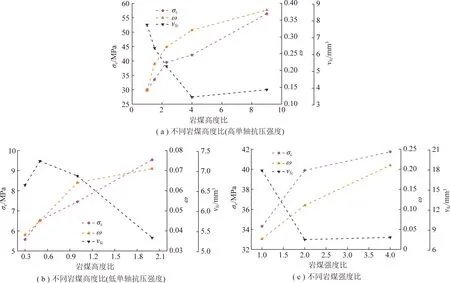
图13 不同组合条件下煤岩组合试样冲击破碎程度

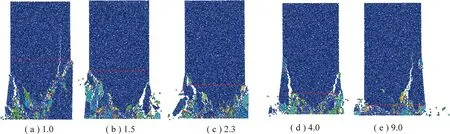
图14 不同岩煤高度比下组合试样破坏特征

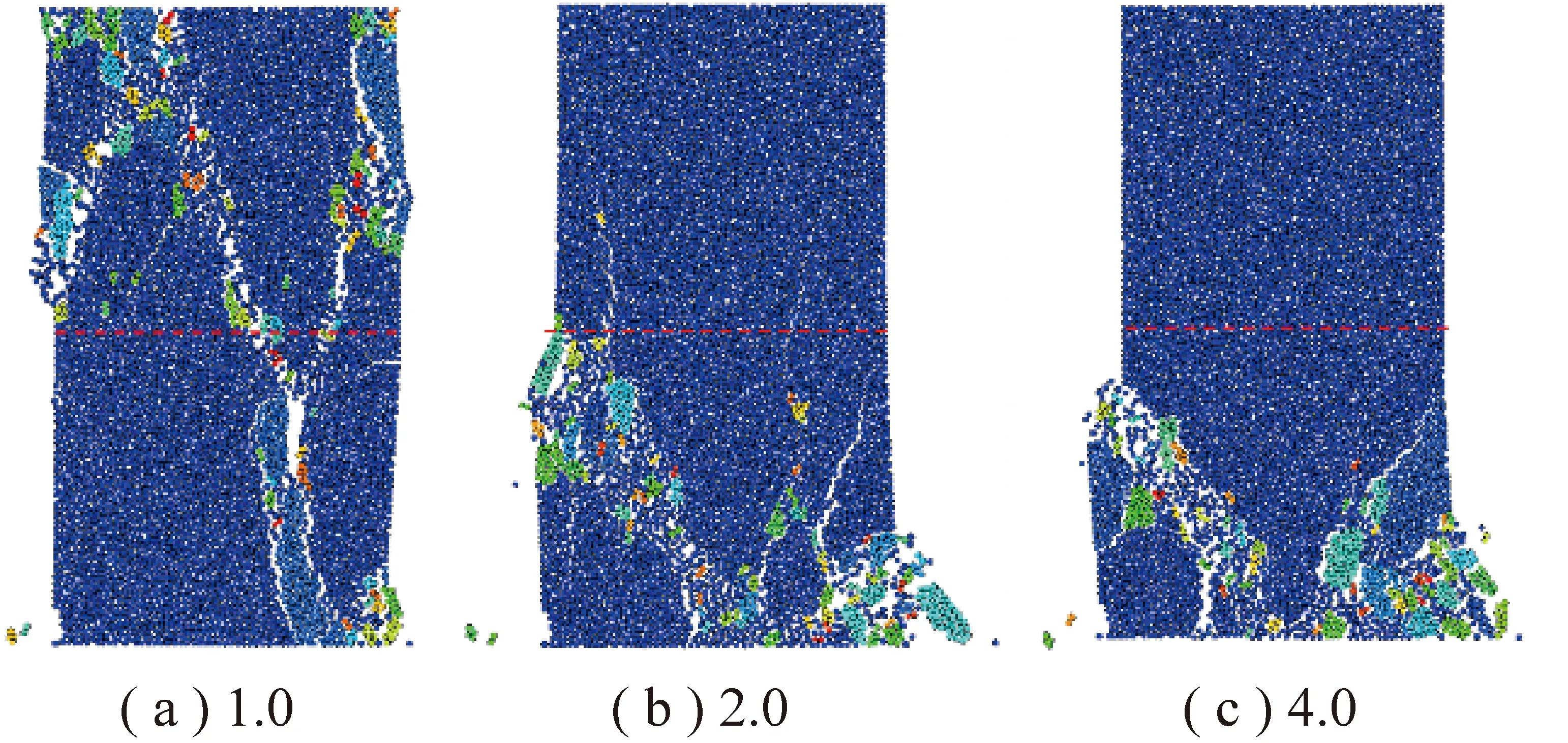
图15 不同岩煤强度比下组合试样破坏特征

表5 煤岩组合试样力学参数模拟结果

下面依据图13的分析结果对煤岩差能失稳指标的合理性进行验证，并与剩余能指数进行对比。由图16(a)可看出，对于第1组数据，随岩煤高度比增大，组合试样的差能失稳指标呈单调增大的趋势，这与试样的冲击倾向性强弱规律表现一致。而剩余能指数并非单调增大，与个别试样实际的冲击倾向性大小关系不符。对于第2组数据，由图16(b)可看出，组合试样的差能失稳指标和剩余能指数均随岩煤高度比增大而单调增大，这与试样实际的冲击倾向性相符。对于不同岩煤强度比的情况，由图16(c)可看出，2个指标也均随岩煤强度比增大呈单调增大的趋势，与图13(c)中组合试样冲击倾向性的分析结果一致。上述分析表明，笔者所提的煤岩差能失稳指标随组合试样冲击倾向性的增强而单调增大，有效验证了该指标评价试样冲击倾向性的合理性。

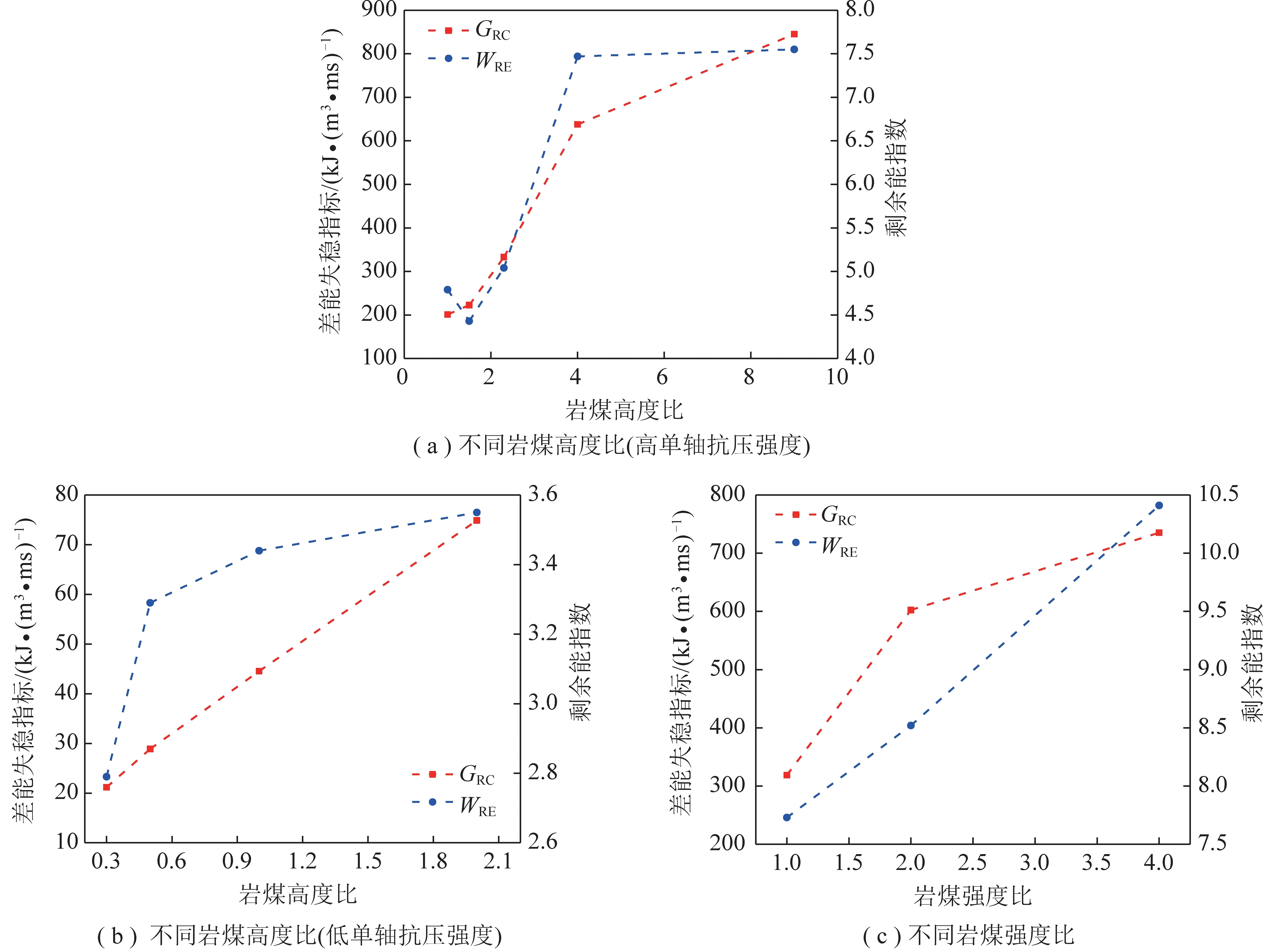
图16 煤岩差能失稳指标合理性验证

图17展示了表5中所有试样的煤岩差能失稳指标与剩余能指数的关系，可看出两者之间具有较强的正相关关系，即差能失稳指标越大，剩余能指数也越大，这进一步表明使用笔者所提的煤岩差能失稳指标来评价组合试样的冲击倾向性具有一定合理性。

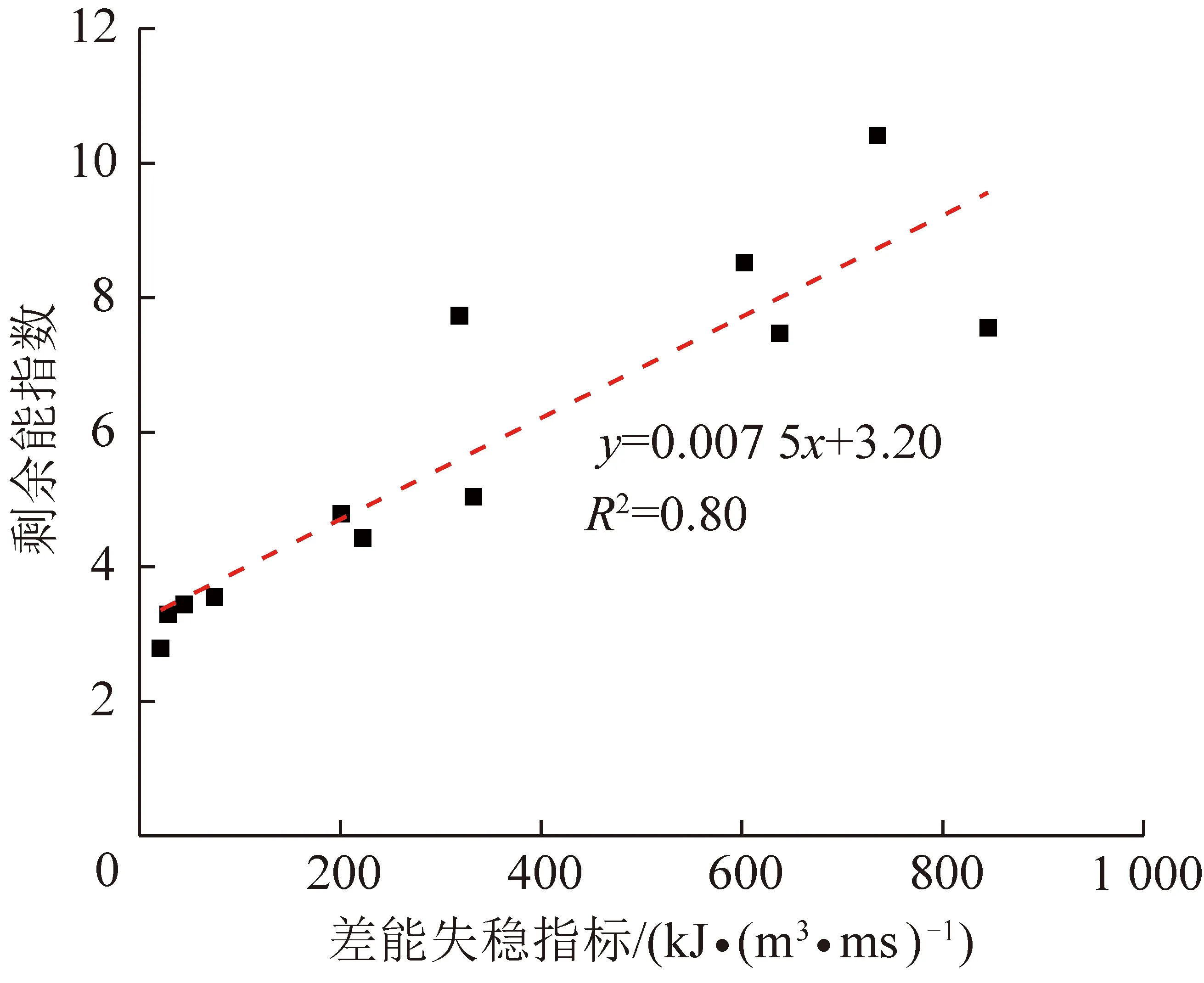
图17 差能失稳指标与剩余能指数的关系

5 煤岩差能失稳指标与现有冲击倾向性指标的联系

目前，我国2010年颁布的GB/T 25217.2—2010推荐了4种煤的冲击倾向性评判指标，分别为动态破坏时间、弹性能量指数、冲击能量指数和单轴抗压强度。其中动态破坏时间是在特定加载条件下(0.5～1.0 MPa/s)得到的煤样从峰值强度到完全破坏所经历的时间，其本质为煤样峰后失稳过程持续时间。对于煤岩组合试样，因其力学特性主要取决于煤体，因此煤的冲击倾向性判别指标对煤岩组合试样同样具有一定适用性。由式(3)可看出，笔者所提的煤岩差能失稳指标综合考虑了单轴抗压强度与煤岩体失稳持续时间Δ等2个参量，若加载速率控制在0.5～1.0 MPa/s，则煤岩体失稳持续时间Δ即动态破坏时间。另外，在采用模糊综合评判方法判定煤冲击倾向性强弱时，，，，四个指标的权重分别为0.3，0.2，0.2，0.3。指标的权重越大，一定程度上表明了该指标与煤冲击倾向性的关系更加密切。可见，煤岩差能失稳指标中包含了煤冲击倾向性评判中2个权重较大的参量。

由煤岩差能失稳指标的定义可知，指标考虑了组合试样中煤体与岩体的峰值弹性能密度这一参量，该参量在评价煤岩冲击倾向性方面具有重要应用。我国2019年颁布的GB/T 25217.3—2019推荐以剩余能量指数来评价煤岩组合试样的冲击倾向性，该指标中也含有峰值弹性能密度这一参量。GONG等基于线性储能规律提出的峰值弹性能量指数、峰值能量冲击指数与剩余弹性能指数3个指标也均采用了峰值弹性能密度这一参量。

笔者所提的煤岩差能失稳指标之所以采用了煤体与岩体的峰值弹性能密度差，主要是从煤岩整体系统的角度出发，考虑了煤体与岩体的力学特性及能量积聚性质的差异。然而，剩余能量指数仍将煤岩组合试样视为单体试样，未考虑煤体与岩体间的能量积聚特性差异。需要说明的是，煤岩差能失稳指标评判组合试样冲击倾向性的等级划分还需要经过大量试验与工程实例来确定，以便更好地应用于工程现场。因煤岩差能失稳指标的大小会受到加载速率量级的影响，从而无法统一评判不同加载速率量级下组合试样的冲击倾向性。鉴于此，笔者建议采用GB/T 25217.2—2010中动态破坏时间的测定方法来开展煤岩组合试样的单轴压缩试验，获得的动态破坏时间即煤岩失稳持续时间Δ，同时也得到了组合试样的单轴抗压强度。然后，分别对煤样、岩样开展常规速率下的单轴压缩试验，得到煤、岩各自的弹性模量。最后，由式(3)即可计算得到组合试样的差能失稳指标。

6 结 论

(1)同一应力水平时，不同类型岩石所具有的弹性能密度主要取决于其弹性模量，且2者呈负相关关系。

(2)煤岩峰值弹性能密度差与抗压强度、煤体弹性模量、岩煤高度比、岩煤弹模比等因素均具有正相关关系，而与岩体弹性模量的关系不明确，且抗压强度是其主控因素。

(3)组合试样中煤体与岩体的峰值弹性能密度差与其最终的破坏程度具有一定关联，即煤岩峰值弹性能密度差越大，往往试样破坏越剧烈。基于非平衡热力学和耗散结构的观点，构建了组合煤岩系统差能失稳分析模型。

(4)提出以煤岩系统的峰值弹性能密度差与失稳阶段持续时间的比值作为评价煤岩组合体冲击倾向性的新指标，本质上表征了煤岩系统失稳过程中储存弹性能的释放速率，并由试验与模拟数据验证了该指标的合理性。