煤层中断层的透射槽波定量响应特征
王保利,金 丹,张唤兰,程建远
(1.中煤科工西安研究院(集团)有限公司,陕西 西安 710077;2.西安科技大学 地质与环境学院,陕西 西安 710054)
据统计,我国煤矿事故中由于地质构造原因引起的事故占比超过70%。我国煤矿地质构造复杂,开采地质条件较差,在这种情况下,未搞清工作面内的地质构造而贸然采掘,极易引发冒顶、片帮、压架、突水以及瓦斯事故等,造成人员和经济损失。因此,超前查明工作面内存在的隐蔽地质构造对煤矿安全高效生产至关重要。
影响煤炭开采的隐蔽致灾地质因素主要包括:断层、陷落柱、煤层厚度突变以及应力集中区等。准确、定量地查明这些地质异常体,可为安全高效回采提供地质保障,这也是我国煤矿高产高效地质保障系统的核心内容。
煤矿安全高效开采,迫切要求能够超前、定量查明小断层、煤层厚度变化、陷落柱、地应力集中区、瓦斯富集带、裂隙发育带等隐蔽致灾地质因素。煤矿井下槽波地震探测技术已在采煤工作面内部隐伏构造探测方面取得了良好的地质效果,但是该技术尚无法实现断层“三要素”(断距、倾角、倾向)的定量判识和煤厚的直接测量,急需开展相关研究以攻克这一技术瓶颈难题。
由于槽波能量对断层更为敏感、直观,因此在断层探测方面应用最为广泛。大部分学者采用振幅衰减系数进行CT反演获得采煤工作面内煤层连续性特征,并据此解释断层产状;由于激发和接收的能量一致性问题,振幅衰减系数法反演精度较差,考虑到槽波的高频和低频分量在经过煤层内的异常构造时,其衰减快慢不一致,因此部分学者采用频率谱相对透射系数法进行断层的CT反演成像。杨元海提出了采用速度谱相对透射系数图法来探测采煤工作面内断层等地质构造,该方法具有原理简单、易于实现且计算量小等特点;周官群等则利用槽波速度对采煤工作面内的断层进行成像,通过速度相对高低来判定断层性质(低速区为逆断层,高速区为正断层),并指出断层断距可依据波速高低进行定性评价,或结合揭露区域类比进行定量评价。除了上述的透射槽波方法外,反射槽波也在断层探测中得到了一定的应用。英国学者MASON等最早进行了一系列反射槽波探测断层的试验研究,并提出了延迟求和的断层成像方法;HU和MCMECHAN提出了反射槽波逆时偏移成像技术,并用于模拟反射槽波成像;王季等提出了基于反射槽波频散相似度的断层成像方法,该方法充分利用了槽波的频散性质,压制了画弧现象,有效提高了断层成像的信噪比和分辨率;金丹提出了时窗能量比值的反射槽波成像方法,来提高反射槽波成像精度;王勃提出利用三分量槽波数据的极化偏移成像方法来消除断层成像假象。梁森、黄超慧等研究了断层的槽波响应特征,对不同断距的断层对槽波的能量和频带进行了半定量分析,但未给出断距和能量之间的定量关系。
上述研究成果表明,在利用槽波进行断层探测时,无论是透射槽波还是反射槽波,可获得断层的走向,并依据相对幅值大致判定断距是否大于半煤厚,但尚不能定量地给出断层断距。同样,在进行数值模拟和物理模拟时,也仅是从定性的角度讨论断层对槽波波场特征的影响,这使得槽波定量探测缺乏理论依据。笔者将从槽波数值模拟角度,分析不同断距断层的槽波波场响应特征,建立断层断距参数与透射槽波多属性之间的定量关系,为断层的透射槽波定量探测提供理论依据。
1 模型设计
为与实际模型更好对比,同时兼顾计算效率,设计的模型大小为544 m×240 m×96 m,包括了在6个面上各16 m的PML边界层。网格采用1 m×1 m×1 m的正方体。
采用的3层模型参数见表1,其中顶板和底板参数一致,为了避免巷道对分析结果的影响,模型中没有加入巷道;煤层埋深40 m(包括模型上部16 m PML边界层);设计的断层位置在=200 m(包括模型左侧16 m PML边界层),走向为方向,平面如图1所示。
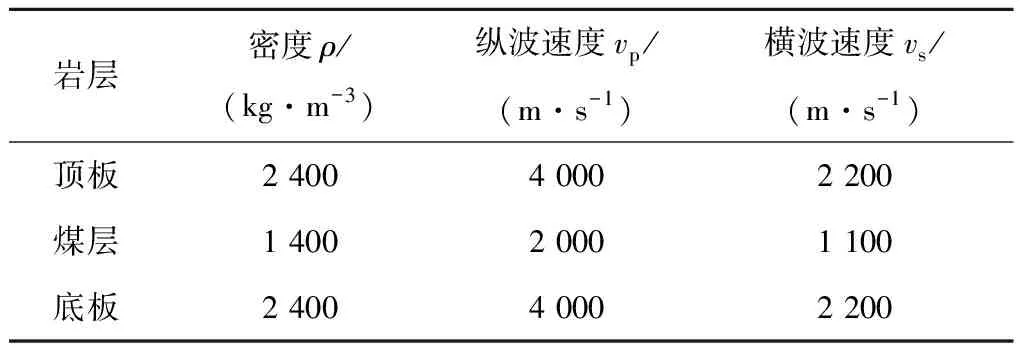
表1 含煤层3层模型物性参数
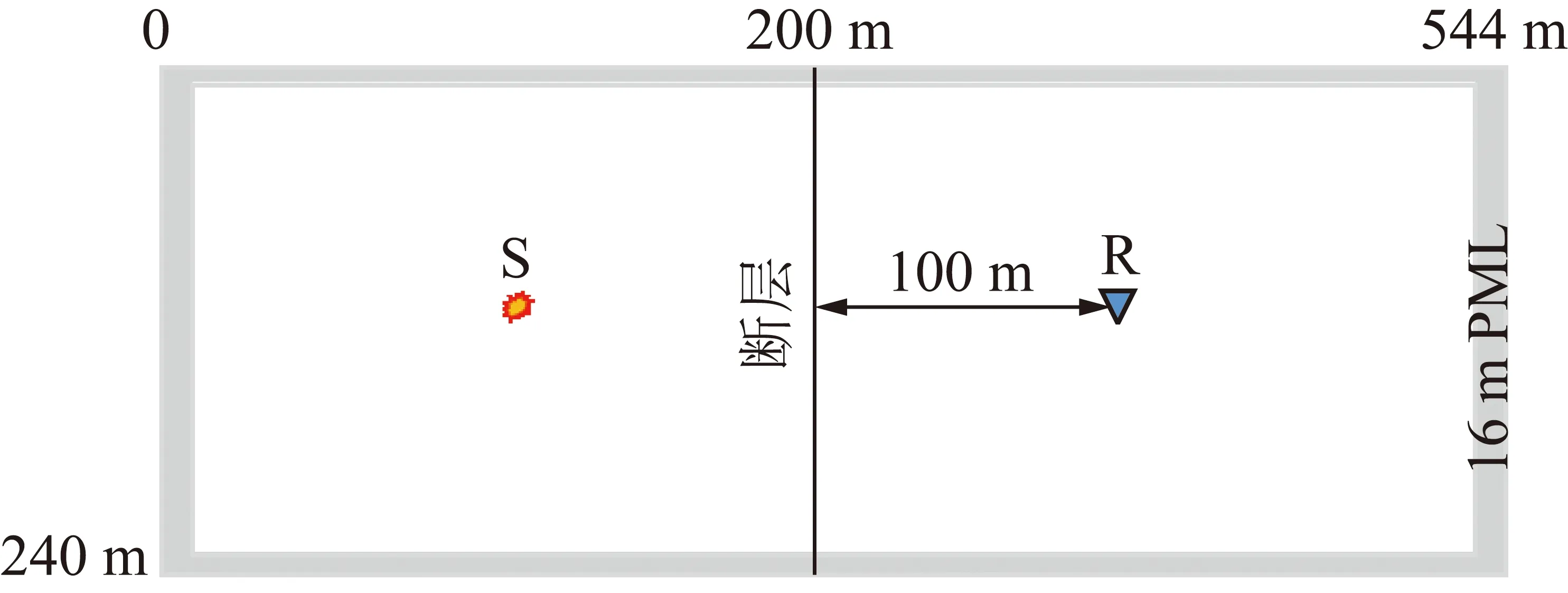
图1 断层模型XY平面
槽波探测断层时,走向可以实现定量探测,但断距难以定量,因此设计断层时,其断距参数的设定主要考虑断距和煤厚的比例关系。具体设计的模型类型见表2,针对5 m煤厚和10 m煤厚的2种煤层分别设计0,1,2,3,4,5,6,8 m和0,2,4,6,8,10,12,16 m断距的断层模型16个,均为垂直断层,断距分别从煤厚的0倍,以0.2倍递增到1.6倍,用以分析不同断距的槽波波场响应。
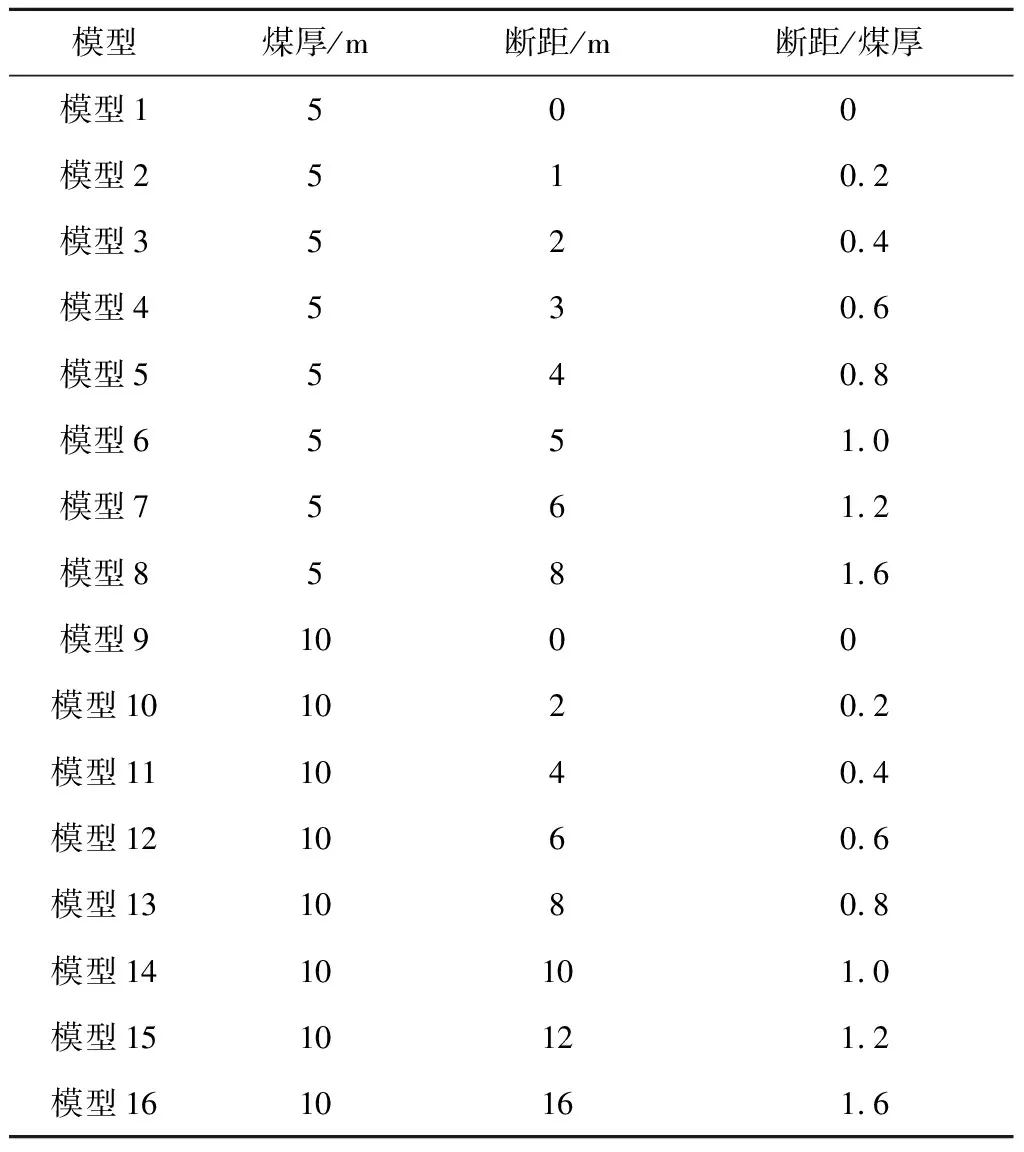
表2 断层模型参数
2 三维三分量槽波数值模拟
利用三维一阶应力-速度弹性波方程,采用二阶时间八阶空间的差分精度求解;同时为避免边界反射对槽波波场的干扰,用PML对边界进行处理;为同时能模拟Love槽波和Rayleigh槽波,采用涨缩源和剪切源2种震源加载方式;考虑到煤厚和槽波埃里相频率的关系,对5 m和10 m煤厚的模型分别采用50~200 Hz和25~100 Hz的宽带Ricker子波,振幅值固定为1.0,0.5 ms间隔采样;为分析断层对透射槽波的影响,在断层左侧100 m处布设震源点S,右侧100 m处布设接收点R。
图2为数值模拟得到的模型1和模型9的三分量记录(三道依次为,和),记录显示三分量记录均有槽波发育,在记录中属于强优势波场。利用多次滤波方法分别计算其群速度频散谱(图3)。图3(a)分别为模型1(5 m煤厚)对应的三分量,,记录,图3(b)分别为模型9(10 m煤厚)对应的三分量,,记录;图3中分量频散谱与理论计算的Rayleigh型槽波基阶(黑线)和二阶频散曲线(白线)吻合、分量频散谱与理论计算的Love型槽波基阶(黑线)和二阶频散曲线(白线)吻合,由于炮检连线平行于方向,因此槽波振型三分量分布与理论吻合;分量Love型和分量的Rayleigh型的基阶能量明显强于高阶能量、分量频散谱较为紊乱。
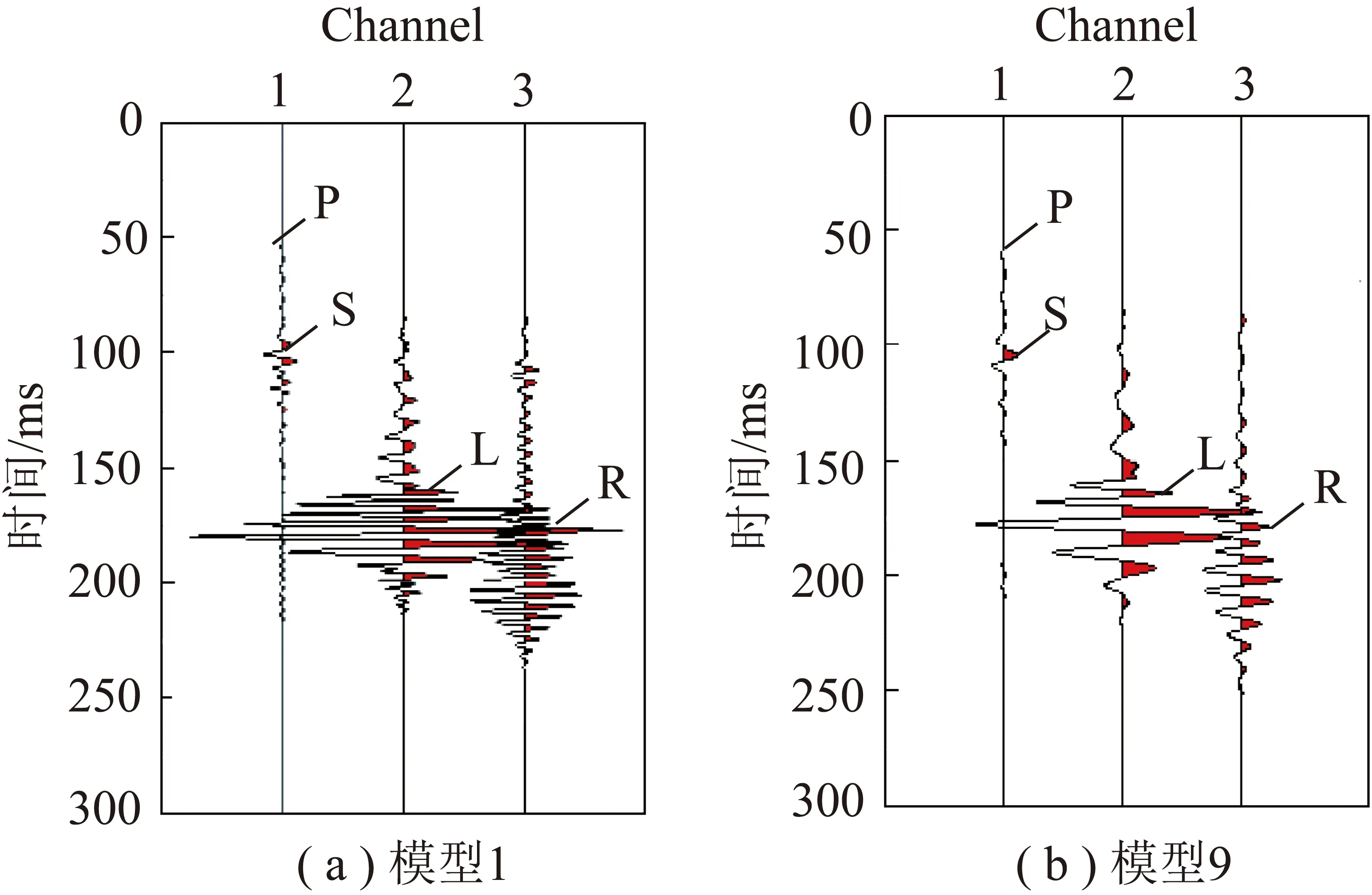
图2 模拟得到的三分量记录(依次为X,Y和Z)
根据上述分析,选定分量和分量记录分别分析Love型和Rayleigh型的基阶透射槽波对断层断距的响应特征。
3 不同断距断层的透射槽波响应特征
3.1 对透射槽波频散曲线的影响
透射槽波在通过断层时,如果对槽波速度产生影响,则该影响最终会体现在频散曲线上,且不同断距的断层,对速度的影响规律同样可在频散曲线中分析得到。为此,笔者在通过对模型1~8(5 m煤厚)的不同断距的透射Love型槽波和Rayleigh型槽波的频散谱上拾取频散曲线(图4),结果显示:无论是Love型还是Rayleigh型槽波,频散曲线几乎没有明显有规律的变化(Rayleigh型槽波100 Hz处的变化应为基阶和二阶叠加所致,其位置如图3(b)分量)。这表明,断层(断面垂直)不会对槽波的频散特征造成影响,也即不会影响槽波传播速度。
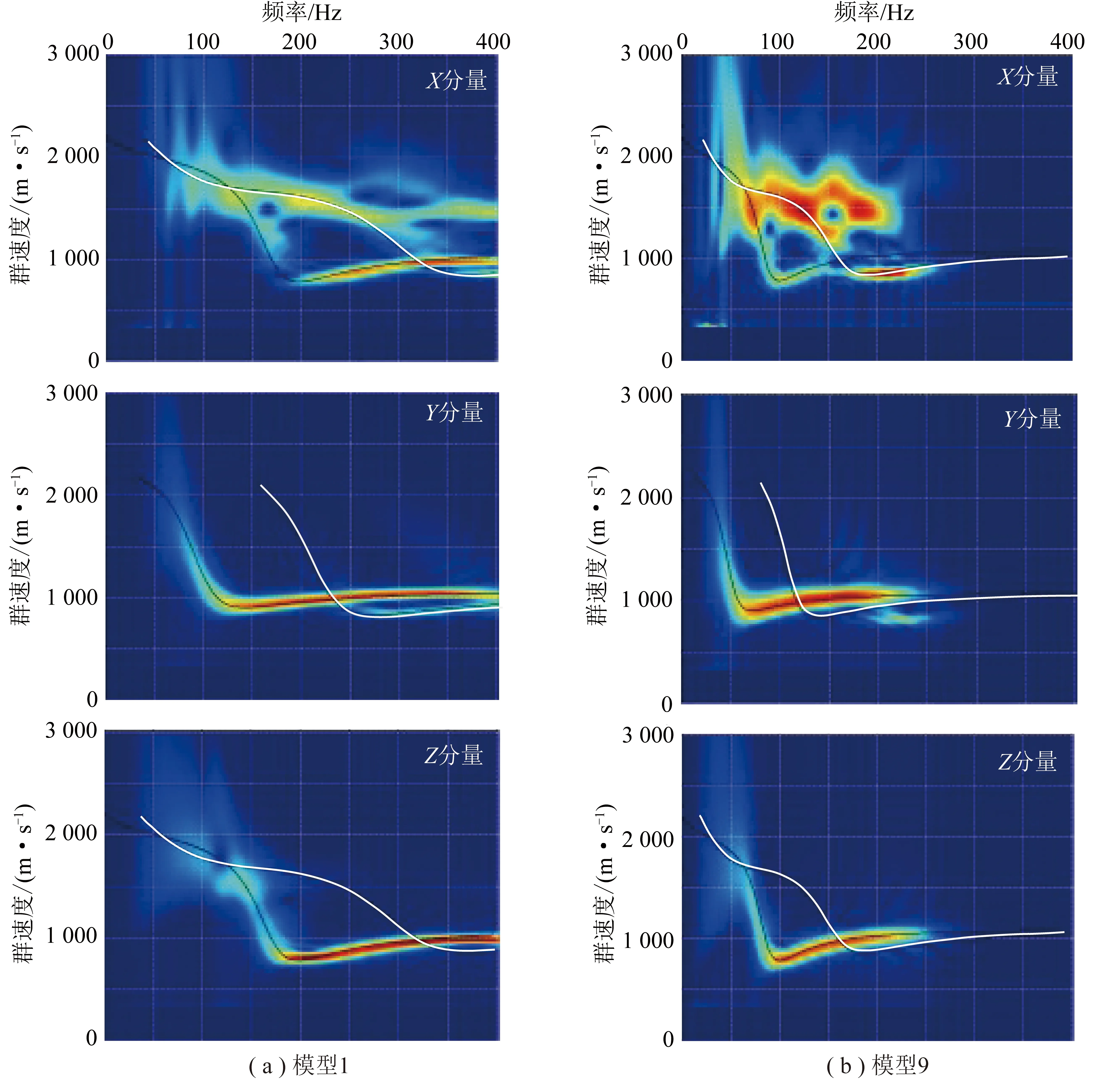
图3 三分量记录的频散谱(黑色尾基阶、白色二阶)
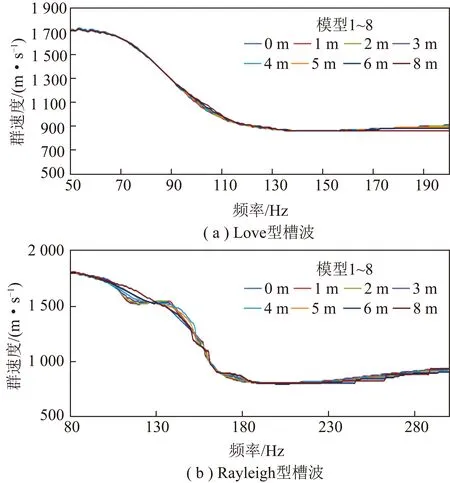
图4 不同断距断层对透射槽波频散曲线的影响
3.2 对透射槽波能量的影响
槽波探测煤层内构造的关键原理是因为煤层内部的构造(如断层)会对槽波的传播产生遮挡效应,从而改变槽波的能量;技术人员通过检测槽波的能量变化获得构造的位置及规模。因此断层对槽波的能量的影响是必须进行精细讨论的,特别是对断层断距的定量探测来说。
一般认为在断层断距大于煤厚时槽波会被完全挡住,从而无法接收到槽波。实际上,根据槽波在煤层深度方向上振幅分布特征,在煤层外侧仍然有一定能量的槽波分布,这些槽波在遇到断层时可以透射进入到断层的另一段内继续进行传播(图5),特别是槽波低频分量。
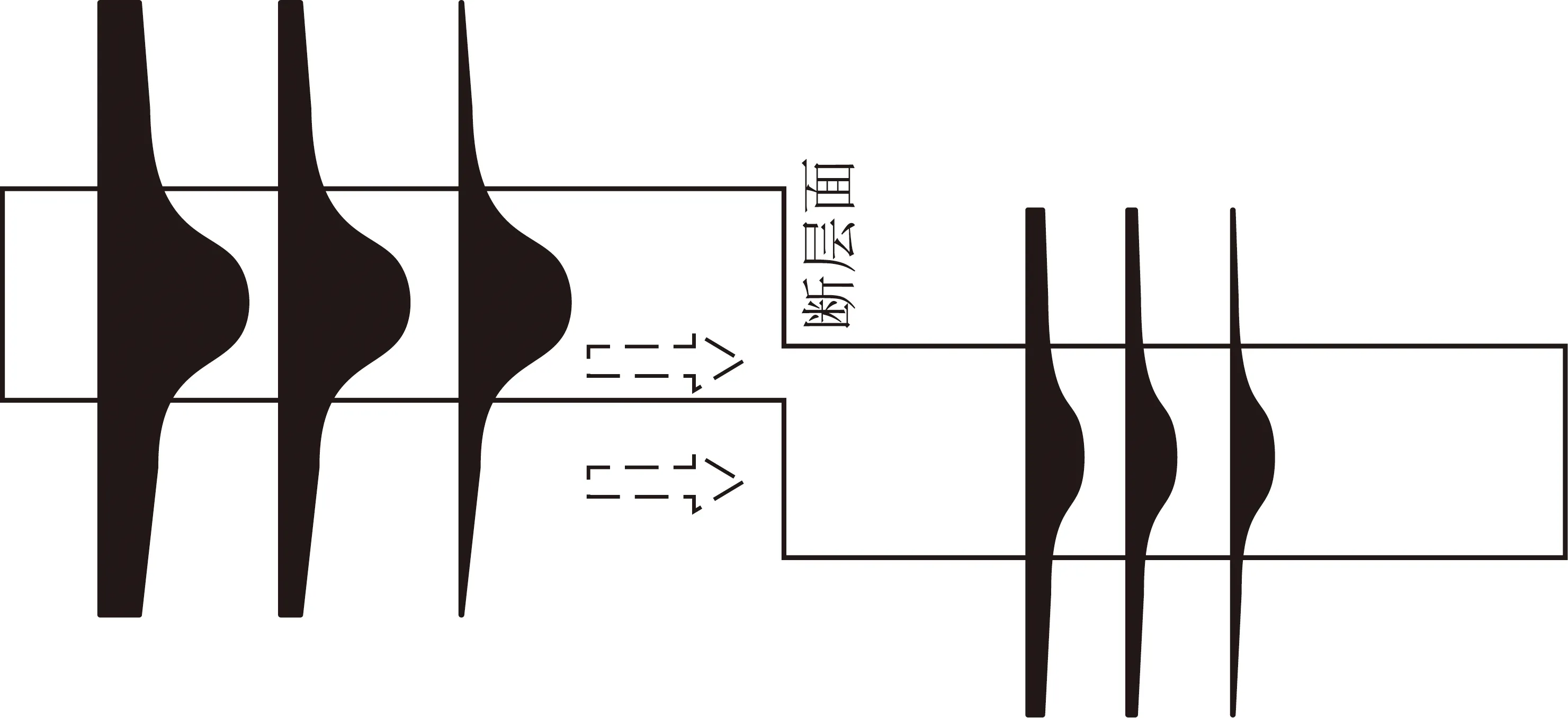
图5 槽波通过断层示意
笔者将在每个记录的频散谱上拾取了基阶槽波频散曲线对应槽波能量,并绘制出不同煤厚、不同断距断层模型中槽波的能量随频率的变化曲线,如图6所示。
图6(a),(c)的Love槽波振幅变化曲线显示,5 m煤厚模型的频率约为10 m煤厚模型的2倍,但振幅约为后者的一半,表明振幅的衰减与频率有一定的关系;在图6(b),(d)的Rayleigh型槽波也有这样的现象,且两者的振幅随频率变化趋势非常一致,这表明断距和振幅的衰减具有一定的定量关系。
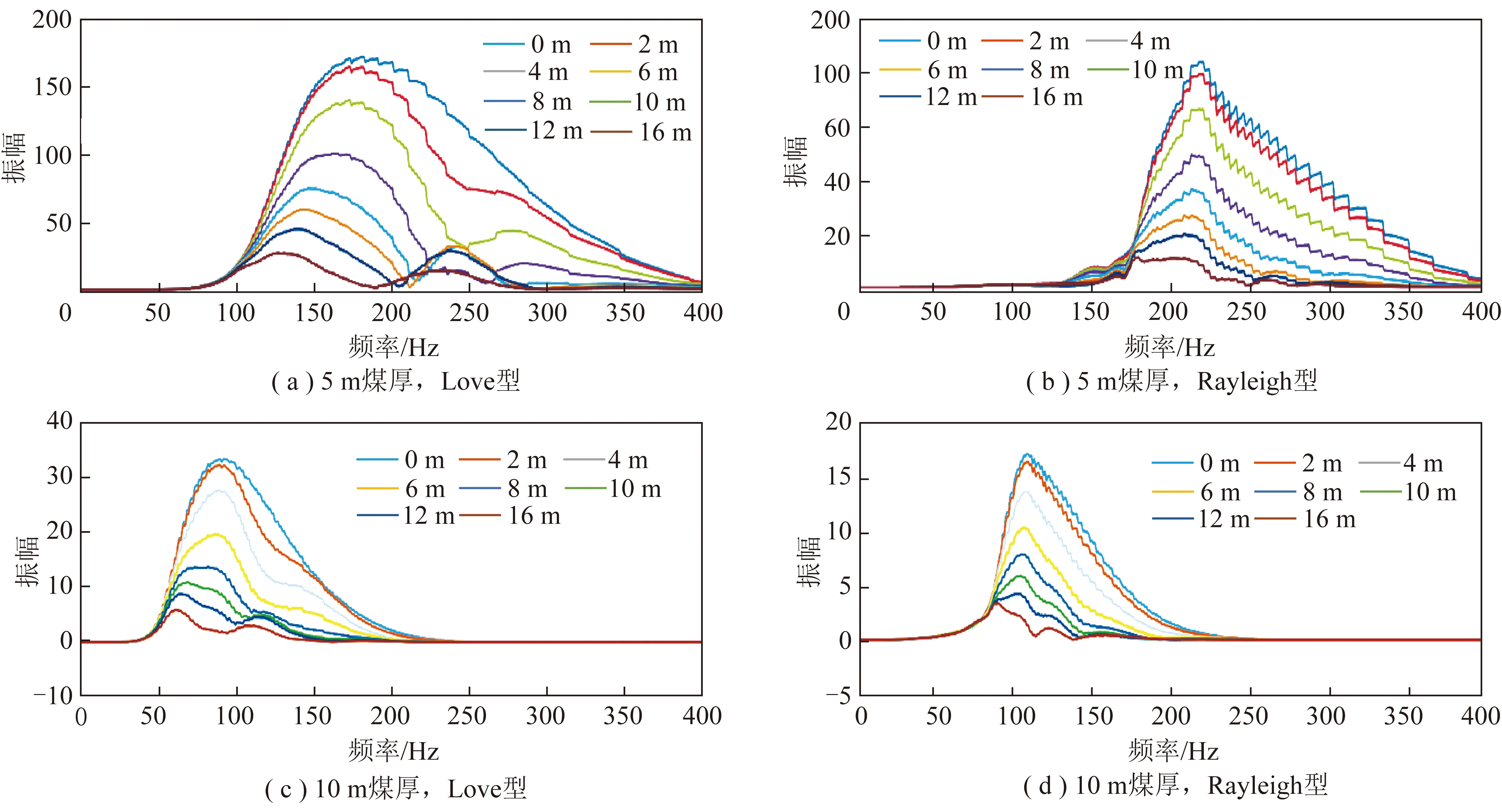
图6 不同煤厚、不同断距的断层对槽波能量的影响
3.3 断距对槽波振幅衰减的定量分析
前面定性地分析了不同煤厚、不同断距的断层对Love型和Rayleigh型基阶槽波的影响,本节将进一步建立断距与槽波能量的定量关系。槽波在过断层时涉及模式转换,理论推导相当困难,笔者主要基于理论记录分析过断层前后槽波能量的定量变化。
设定图1中震源点S激发的信号用()表示,在没有断层存在的情况下(如模型1和模型9),在接收点R接收到的槽波表示为
(,)=()e-ei
(1)
在断层存在时,槽波穿过断层使得能量发生变化,将断层对槽波能量的这种衰减作用采用品质因子进行等效:
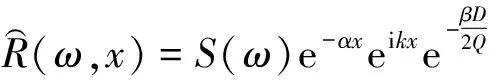
(2)
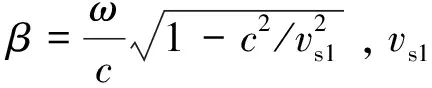
根据式(1),(2)可得到断层对槽波的影响:
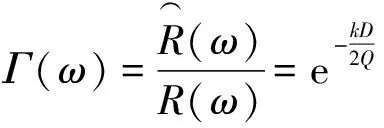
(3)
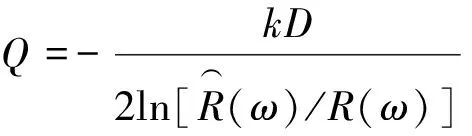
(4)
表2中的18个模型中,模型1和模型9分别为5 m煤厚和10 m煤厚无断层模型,因此在计算时可作为式(4)中的(),从而计算出每个断层模型Love型槽波等效和Rayleigh型槽波等效,如图7所示:横轴为波长/煤厚,可以消除煤厚的影响,从而将不同煤厚进行统一对比分析;为更精确分析能量衰减,分别选取Love型槽波和Rayleigh型槽波的埃里相之后,高阶槽波到达以前的槽波,其中Love型槽波波长分析范围为1.5~2.5,Rayleigh型槽波分析范围为1.0~1.8,下限基本等于埃里相波长;对比发现,对同一类型的槽波,在=(为断距,定义为规格化断距)相同时,其衰减量基本相同;规格化断距相同时,衰减量几乎呈水平直线,表明与槽波波长(规格化后,即)无关;对比Love型,Rayleigh型的衰减发现,规格化断距相同时衰减量也基本相同。
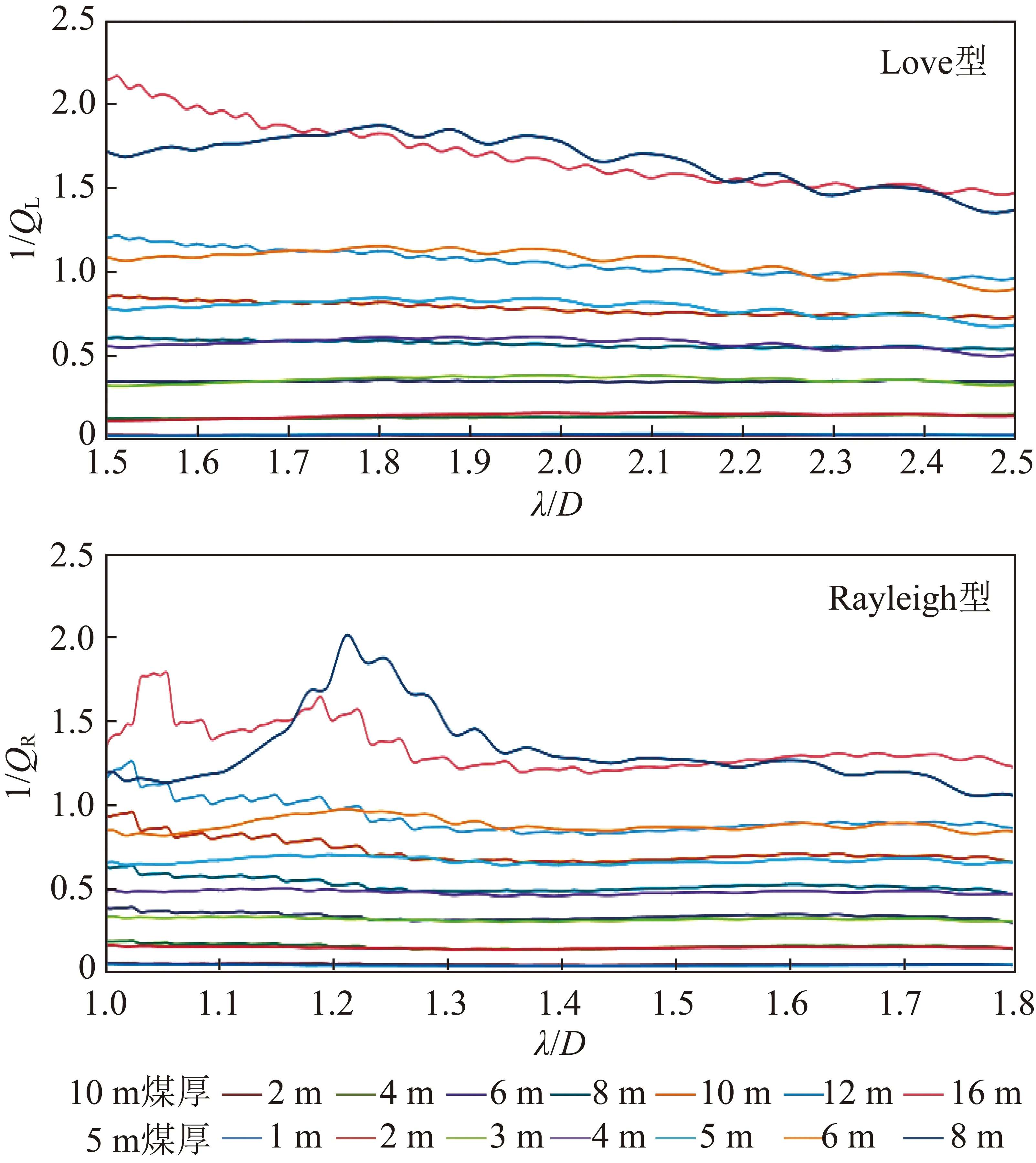
图7 不同煤厚、不同断距槽波衰减与波长的关系
在近似认为衰减量与槽波波长无关情况下,沿着图7的横轴,可求出不同煤厚、不同规格化断距对应的等效(图8),分析可得:不同煤厚、相同振型的槽波,规格化断距和等效具有相当好的一致性;Love型槽波和Rayleigh型槽波同样具有很高的一致性,Love型槽波;随着规格化断距的增加,Love型槽波和Rayleigh型槽波的越来越小,表明其衰减量随着规格化断距的增大而增大;规格化断距在=1/2(也即断距为半煤厚左右)前后的变化呈现不同的斜率,在≤1/2时,等效随规格化断距呈现快速下降趋势,而在>1/2时,以较缓的斜率线形下降,前后斜率差异达到8倍。
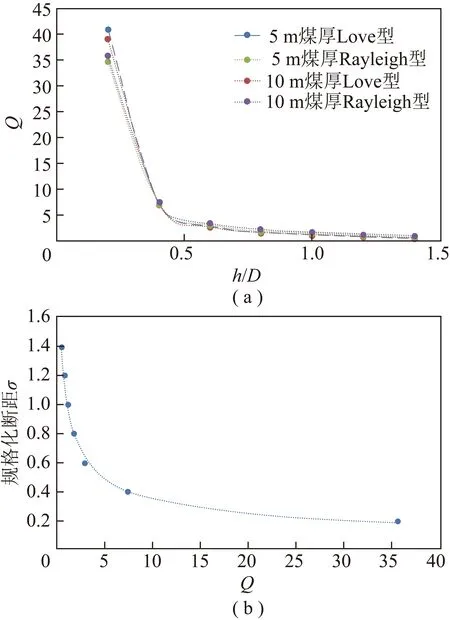
图8 规格化断距σ与等效Q定量关系
采用多项式拟合图8(a)中的4条曲线的平均(拟合曲线如图8(b)中虚线),可得到规格化断距与等效值之间的定量换算关系:

(5)
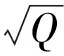
4 结 论
(1)垂直断层不会影响槽波的频散特征,只对槽波的能量有明显的影响。
(2)模拟显示,即便断层断距大于煤厚,仍然会有相当的槽波能量通过,特别是长波长分量。
(3)在槽波波长与煤厚相近时,相同规格化断距的断层对槽波的衰减量不随槽波波长变化,且Love槽波和Rayleigh槽波衰减量几乎相同。
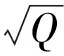
上述结论仅仅是基于理论模拟得出的,其用于实际勘探时仍需要进一步研究。下一步将研究如何在实际数据中应用本文提出的断距定量关系式实现断层断距的定量探测。

