基于并行深度孤立森林算法的水质异常数据检测

王海龙，李东波，吴绍锋

(南京理工大学机械工程学院，江苏 南京 210094)

水作为人类赖以生存的资源，其质量对人类本身和人类社会的良好发展有着很大的影响。随着我国经济不断发展，人民对于水资源的质量要求也日益提高，如何严格把关水质以保证人民良好的生活需要和基本利益是各级政府面临的一个难题。

传统水质异常检测算法经常采用阈值，试图发现那些不属于正常区域的异常点，即根据经验或者数据内容定义一个范围[n,k]，取值不在该范围的即是异常数据，这种基于阈值的方法看似简单，但是往往是不准确的，原因如下：1)一类事物往往是具有多特征的，类别的判定应是基于各个特征的共同计算得到的，而不是简单的基于某一特征；2)异常数据和正常数据间的界限往往不精确；3)阈值判断不一定适用每一个水域，同时正常的数据根据时间和其他因素影响也是不断发展的，目前的正常概念可能随着时间推移将不再适用。

目前，国内外很多学者已经采用了大量的水质异常数据检测方法实现水质异常数据的检测：Byer[1]假设水质指标服从高斯分布，计算得到样本数据的平均值与方差，将实际监测到的每个时间点上水质指标数据测量值与样本水质指标数据时间序列的平均值进行比较，如果差值的绝对值大于样本数据的3倍方差，则当前水质被判定异常；Conde[2]利用人工神经网络等机器学习相关算法，结合监测站点的水质指标数据信息进行建模，通过训练生成分类器来在线判别水质是否正常。

在当前的信息化时代，水质数据通过物联网传输至平台，随着数据不断地产生，上述基于统计和神经网络的方法尽管可靠性较高，但是计算繁琐、效率较低，不适用于对实时性要求较高的水质异常数据检测[3]。

为了解决上述问题，本文引入了孤立森林算法和深度孤立森林算法。孤立森林算法是一种高效的异常检测算法，它利用异常点数量少、异常数据特征值和正常数据差别大两个特点来孤立异常点，算法的效率和可靠性都比较高；而深度孤立森林算法是对孤立森林算法的优化，基于多粒度扫描和级联森林来改进孤立森林算法对局部异常点识别不准确的情况。由于深度孤立森林相比孤立森林多了多粒度扫描阶段和级联森林阶段，会增加一些时间开销，因此本文通过并行化构建孤立森林，从而抵消部分增加的时间开销。

1 水质异常数据分析

异常数据是某个数据集中存在但不合群的数据点，又称离群数据。某一个数据集在多个特征集合上形成一定规律，而集合中有一数据点明显不符合该规律，则该数据点为异常点。

本文数据来自于国家地表水水质自动监测实时数据发布系统的真实数据，见表1。

表1 原始水质数据

为了得到可靠的实验结果，现对水质数据进行以下预处理：

1)水质等级Ⅳ以下的数据使其标签为1.0，代表正常数据；水质等级Ⅳ及以上的数据使其标签为0.0，代表异常数据。

2)删除属性都缺失的数据。

3)因为原数据集合中有缺失的数据，能够凭借着剩余属性判别水质等级，若在此填充中位数、均值或者插值，在不知原数据集合判别标准的情况下，数据集合将变得不可靠，故将缺失值填充为0。

4)删除缺少水质等级的数据。

处理后的水质数据见表2。

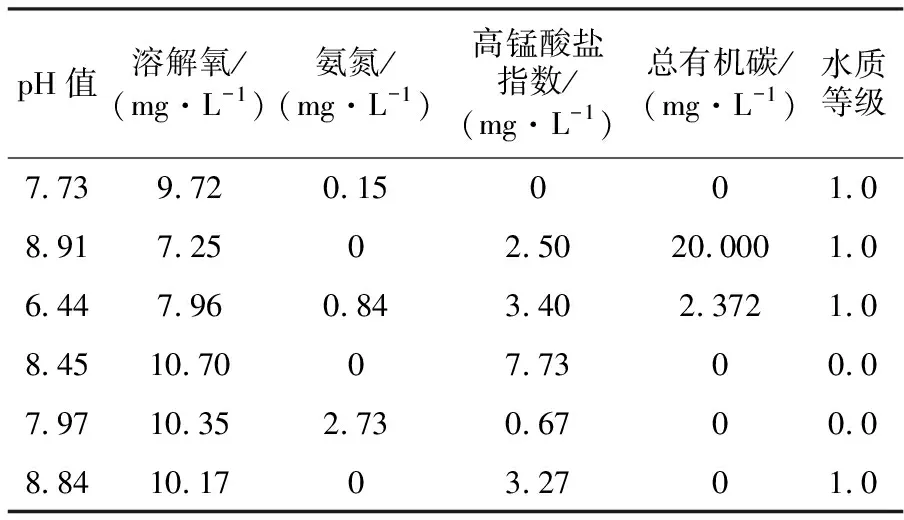
表2 预处理后水质数据

对水质数据进行描述性分析，结果见表3，可以发现异常数据和正常数据在氨氮、高锰酸盐、总有机碳几个指标上差异明显，而pH值和溶解氧则差异较小。

表3 水质数据描述性分析

根据表2生成各指标数据分布图，如图1所示，发现异常数据的溶解氧、高锰酸盐、氨氮等指标相较正常数据波动较大，且存在少数局部异常值。图中深色线代表异常数据，浅色线代表正常数据。

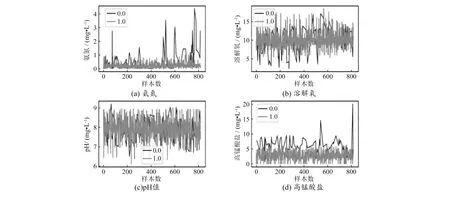
图1 各指标数据分布图

通过分析和经验判断，发现水质数据往往具备以下特点：1)正常数据和异常数据在高锰酸盐、氨氮等指标上有明显差异，而pH值和溶解氧差异较小；2)异常数据较正常数据各指标通常有着较大波动，且有较多远离正常标准的值，整体分布较为稀疏；3)存在少量异常值；4)指标易受气候、人工等因素影响；5)水质数据维度较低，异常数据数量少。

2 基于多粒度扫描孤立森林的水质异常检测

2.1 孤立森林算法

孤立森林算法是一种基于规律，针对异常点是分布稀疏且离密度高的群体较远的点，通过从数据集合随机地获取属性，再随机地获取某条数据，该属性所对应的值作为划分阈值从而将数据集划分为两个部分，不断重复上述步骤，直至使得某部分数据集的数据量小于等于1，即孤立某条数据的算法。实验表明，正常数据被孤立的平均路径长度即划分次数，是异常数据的2～3倍，如图2所示，也就意味着相比正常数据，异常数据往往在更少的划分次数下就能使其孤立[4-5]。

图2 数据平均路径长度

孤立森林通过给定的数据集，每次从中抽取固定大小的子数据集构成子树，通过构建大量的子树形成森林，计算每条数据被孤立或者找到其在树中的位置所花费的路径长度，计算其异常得分，判断当前数据是否异常。

给定一个包含n个样本的数据集，树的平均路径长度为：

(1)

式中：H(i)为调和数，该值可以被估计为ln(i)+0.577 215 664 9；c(n)为给定样本数n时路径长度的平均值，用于标准化样本x的路径长度h(x)。

样本的异常得分s(x,n)定义为：

(2)

式中：E(h(x))为样本x在一批孤立树中找到自己应该所处的位置所花费的平均路径长度。

由式(2)可以得出以下结论：

1)当E(h(x))→c(n)，s(x,n)→0.5,则不能区分样本x是不是异常点。

2)当E(h(x))→0，s(x,n)→1.0，则能够判断样本x是异常点。

3)当E(h(x))→n-1，s(x,n)→0，则能够判断样本x是正常点。

2.2 深度孤立森林

深度孤立森林由多粒度扫描和级联森林两部分组成，多粒度扫描负责以不同特征维度生成新的数据集合，级联森林负责接收和训练多粒度扫描所产生的新数据集合，

2.2.1多粒度扫描

定义特征集合为F，扫描窗口大小为p，根据窗口p构建新的特征集合，定义步长为step，在特征集上进行滑动，得到式(3)所示的数量子特征集合S，其中每个子特征集的标签仍使用原标签，而多粒度则意味着基于不同的窗口大小和步长能获取不同数量和维度的子特征集合。

(3)

多粒度扫描的滑动窗口过程如图3所示，在图中窗口大小为100，步长为1，随着窗口不断滑动，根据式(3)，最终能够得到301个维度为100的子数据集合，同时步长step越大，损失的特征信息越多；步长step越小，产生的子特征集越多，窗口滑动和子特征产生的时间开销越大。

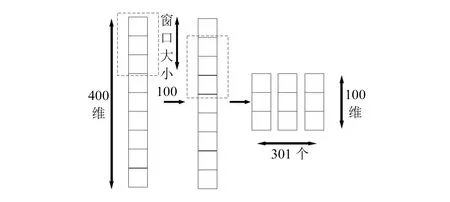
图3 多粒度扫描示意图

在图4中，窗口大小为200，步长为1，根据式(3)，最终得到201个维度为200的子数据集合。

将图3中生成的特征集合分别输入到普通随机森林和完全随机森林中，其中完全随机森林和普通随机森林的不同点在于完全森林中每一棵树都可以通过随机地选择一个特征来分裂树的每个节点，而普通随机森林通过最佳的gini值作为分裂特征。假设图3中所得到的301个100维特征向量每一个对应一个三分类的类向量，即三分类的概率分布，经过普通随机森林和完全随机森林的计算，分别得到了301个3维的类向量，再将该向量进行聚合，得到了一个903维的特征向量，最终再将完全随机森林和普通随机森林的特征向量聚合，生成一个1 806维的向量，同理，图4中生成的特征集合按照上述计算会得一个1 206维的向量，再和上面生成的1 806维向量进行拼接生成一个3 012维的向量作为级联森林阶段的输入，如图5所示。

图4 多粒度扫描示意图

图5 多粒度扫描阶段

2.2.2级联森林

级联森林阶段如图6所示，将多粒度扫描阶段根据不同窗口大小和不同步长所得到的特征拼接，作为级联森林的输入，每一层的输出作为下一层的输入，将最后的输出取平均再取其中最大的值，得到最大值所对应的类别作为最终的结果。级联森林的层数通常有着自适应调节的能力，即在级联森林的构造阶段，在构造当前层时，如果经过交叉验证的准确率相较上一层没有提升或者提升小于阈值，则停止级联森林的构造，因此也会节省算法训练的时间开销。

图6 级联森林示意图

2.3 算法构建

2.3.1并行孤立森林构建

孤立森林分为训练阶段和评估阶段。训练阶段主要目标是分配数据集中各数据点在树中的位置，在本文中，对孤立森林进行了并行优化，即根据 的数量创建n条线程，每条线程各自建树，互不影响，其中建立森林的伪代码如下：

输入：水质数据集X，异常得分阈值S，iTrees数量n，子样本数量s

输出：IForest(iTrees,s,S)

1：最大深度max_length=ceiling(log2n)

2：子样本subsample_size=min(s,X.size)

3：获取特征数num_features=X.cols

4：初始化当前深度current_length=0

5：创建线程池

6：创建存放线程集合list

7：for i=1 to t do

8：创建线程tThread

9：存放线程list.add(tThread)

10：end for

11：利用java8的stream和lambda表达式进行并行化计算得到ListIForest

12：return IForest

线程内部伪代码如下：

输入：水质数据集X，子样本数量s，最大深度max_length，特征数num_features，当前深度current_length

输出：tThread

1：创建线程tThread

2：初始化tThread

3：X′=sample(X,s)

4：iTree=growTree(X′,max_length,num_features,current_length)

5：return iTree

详细建树伪代码如下：

输入：子水质数据集X′，最大深度max_length，特征数num_features，当前深度current_length

输出：ITree

1：if current_length >= max_length or X′.size <=1

2：return LeafNode(X′.size)

3：Q是数据集X′的特征集，随机取某一特征q∈Q,随机取p,其范围是特征q的取值范围

评估阶段根据训练阶段所构建好的森林，计算找到某数据点所花费的路径长度，并根据式(2)得到其异常得分和判断其是否为异常数据点，其伪代码如下：

输入：水质数据集创建的孤立森林T，某条水质数据x，异常得分阈值S

输出：是否为异常值

1：计算寻找x在T中的位置所花费的距离l

2：根据公式(2)计算异常得分s

3：if s>S

4：return-1

5：else

6：return 1

2.3.2并行深度孤立森林构建

由2.2可知，深度孤立森林划分为多粒度扫描阶段与级联森林阶段，其中多粒度扫描阶段的伪码如下：

输入：水质数据集X，维度u，步长step，窗口p

输出：新数据集X′

1：if p>u

2：return X

3：start=0

4：X′= {}

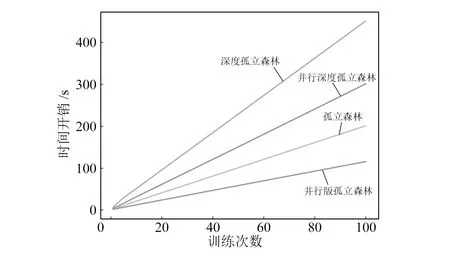
5：while start+step

6：Xj=GenerateDate(X,start,p)

7：X′+=Xj

8：start+= step

9：end while

10: return X′

级联森林阶段的伪码如下：

输入：多粒度数据集X′

输出：结果类别c,层级数depth

1：X = concatenate(X′)

2：for i=1 to depth do

3：tmp1 = NormalForest(X)

4：tmp2 = IsolateForest(X)

5：X = concatenate(tmp1,tmp2)

6：end for

7：X = Avg(X)

8：c = argmax(X)

9：return c

3 仿真结果及分析

3.1 仿真环境

用于仿真的计算机CPU为Intel(R)Core(TM)i5-7300HQ@2.50 GHz，内存为12 GB，操作系统为64位Windows10。

3.2 仿真结果及分析

对孤立森林算法和深度孤立森林算法进行测试，取子树的数量区间为[1,1 000]，基于不同子树数量运行两种算法10次求和取平均值，结果如图7所示，可以看到，深度孤立森林算法的准确率始终大于孤立森林算法，尤其在子树数量较少的情况下，深度孤立森林算法有很好的性能，但是相比较孤立森林算法波动性较大。

图7 准确率变化图

选取子树数量为500棵，对4种算法训练不同次数，结果如图8所示，并行版的算法相较于普通版本的算法都有着一定的训练效率提升，但是由于并行深度孤立森林算法仅仅优化了级联森林阶段，故并行深度孤立森林的时间开销还是大于普通孤立森林。

图8 各算法时间开销

选取多种异常检测算法，对数据进行测试，结果如表4和图9所示，其中F1代表着精确率和召回率的调和平均值，其综合考虑了精确率和召回率，能够更加准确描述算法的性能。one-class SVM和LOF尽管在整体数据上表现尚可，但是在异常数据上表现非常差，其中one-class SVM仅预测出54.1%的异常数据，LOF仅预测出42.0%的异常数据，而孤立森林和深度孤立森林无论在整体数据，还是在异常数据上，都远远优于one-class SVM和LOF，且深度孤立森林在异常数据的预测准确率上要优于孤立森林。

4 结束语

本文所应用的深度孤立森林算法，相较于其他异常检测算法，在水质异常数据异常检测上准确率非常高，但所花费的代价是增加了算法训练的时间开销。由于森林是一种天然支持并行化的结构，故提出并行孤立森林和并行深度孤立森林以减少算法训练时间，异常检测的两个重要点在于实时和准确，通过文中分析可知，并行深度孤立森林能够很好地满足这两点。