基于SVD和Cholesky求逆方法的精密单点定位研究

王彬彬，易卿武,2，高 铭，盛传贞，应俊俊，杨建雷，赵精博

(1.中国电子科技集团公司第五十四研究所 卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081;2.西安电子科技大学 电子工程学院，陕西 西安 710071;3.中国科学院精密测量科学与技术创新研究院 大地测量与地球动力学国家重点实验室，湖北 武汉 430071)

全球卫星导航系统是一种利用卫星测距信号为用户接收机提供全天候和高精度的定位、导航、授时服务(Positioning,Navigation and Timing,PNT)的现代化系统，并且在重力反演、海面测高等现代大地测量中具有重要的研究价值[1-2]。精密单点定位(Precise Point Positioning,PPP)作为一种全球卫星导航系统(Global Navigation Satellite System,GNSS)高精度定位算法，其能够精确地估计接收机的绝对坐标[3]，已被广泛应用于地壳形变监测、低轨卫星定轨、空间大气监测和时间同步等领域[4-9]。PPP算法的难点在于数学模型中待估参数过多，达到5+N个，其中N为观测卫星数。因此，参数估计会对PPP的处理结果产生重要影响，尤其是矩阵求逆方法更是直接决定了PPP的定位精度和时效性。

矩阵求逆是矩阵论的重要内容，矩阵论中的广义逆能够解决工程应用中的大量离散数学问题，在数理统计、系统理论、优化计算和控制论等多领域中有重要应用[10]。矩阵分解是一种有效的广义逆的求解方法，常用的矩阵分解求逆方法包括正交三角分解、Cholesky分解和奇异值分解(Singular Value Decomposition，SVD)等。相关研究者在大地测量及相关领域对矩阵求逆方法开展了较为深入的研究工作。在海洋数据同化中，SVD分解、LU分解、正交三角分解的计算效率不同[11]。基于即现场可编程门阵列(Field-Programmable Gate Array,FPGA)平台的Cholesky分解求逆法具有较高的计算效率[12]。此外，矩阵分块运算也可采用矩阵分解求逆的方法[13]，其能够提高平差解算的精度和可靠性[14]。

为了研究不同矩阵求逆方法在PPP算法中的具体计算效果，首先介绍矩阵求逆的基本概念，包括广义逆、SVD分解求逆和Cholesky分解求逆。其次，针对高精度GNSS数据处理的复杂过程，论述PPP算法的实现步骤，包括建立观测方程和参数估计方法。最后，结合iGMAS观测站数据，分别统计采用SVD分解求逆法和Cholesky分解求逆法的动态PPP定位精度和计算所需时间，用以验证两种矩阵分解求逆方法在GNSS精密单点定位算法中的应用效果。

1 矩阵求逆

1.1 广义逆

广义逆是线性代数中针对矩阵的一种运算[15]。一个矩阵A的广义逆叫作A的广义逆矩阵，具有部分逆矩阵的特性。假设一矩阵A∈m×n及另一矩阵Ag∈m×n，若Ag满足A·Ag·A=A，则Ag即为A的广义逆矩阵。广义逆也称为伪逆，是针对非可逆矩阵求解出与可逆矩阵类似特性的求逆方法。任意矩阵都存在广义逆阵，若某一矩阵存在逆矩阵，逆矩阵即为其唯一的广义逆阵[7]。考虑以下线性方程

A·x=y

(1)

式中：A为n×m的矩阵；y∈(A)，是A的列空间。若矩阵A为可逆矩阵，则x=A-1·y是方程式的解。若矩阵A为可逆矩阵，则

A·A-1·A=A

(2)

假设矩阵A不可逆，或者是n≠m，需要一个合适的m×n矩阵G，即

A·G·A=A

(3)

因此，G·y为线性系统A·x=y的解。同样，对于m×n阶的矩阵G

G·A·G=G

(4)

成立。那么，广义逆阵可定义为假设一个n×m的矩阵A，m×n的矩阵G可以使A·G·A=A成立，矩阵G即为A的广义逆矩阵。

广义逆矩阵理论可用于推导线性方程组的解。对于上述任何一种广义逆阵都可以用来判断线性方程组是否有解，若有解时列出其所有的解。若以下n×m的线性系统

A·x=b

(5)

有解存在。其中：向量x为未知数；向量b为常数。那么，广义逆矩阵理论得到的解为

x=Ag·b+[I-Ag·A]·w

(6)

式中：I是单位矩阵；参数w为任意矩阵，而Ag为A的任何一个广义逆矩阵。线性系统解存在的条件是当且仅当Ag·b为其中一个解，也就是当且仅当A·Ag·b=b。

当矩阵为方阵时，矩阵分解是一种有效的广义逆矩阵求解方法，通过将一个矩阵拆解为多个矩阵的乘积。常用实现一些矩阵的快速运算，包括三角分解、满秩分解、QR分解、Jordan分解、Jacobi分解、SVD分解和Cholesky分解等。下面主要分析SVD分解和Cholesky分解在矩阵分解求逆中的方法和效果。

1.2 SVD分解求逆

SVD分解是主成分分析、智能计算、机器学习和自然语言处理等领域的基础[16-17]。而SVD分解求逆则是通过构造特征值和特征向量，对矩阵进行奇异值分解，从而便于矩阵求逆运算。对于矩阵M，其与特征值和特征向量的关系为

M·x=λ·x

(7)

式中：λ是矩阵M的一个特征值；x是对应的特征向量。对于n维矩阵M，如果求出所有的特征值λ1,λ2,…,λn，以及对应的特征向量{x1,x2,…,xn}，那么矩阵M可分解为

M=U·Σ·V*

(8)

式中：U为特征向量{x1,x2,…,xn}构成的n维矩阵，V*是矩阵U的逆矩阵。Σ则是特征值λ1,λ2,…,λn构成的对角线矩阵，特征值也被称为奇异值。因此，式(8)为矩阵M的奇异值分解。

奇异值分解可以被用来计算矩阵的逆矩阵。若矩阵M的奇异值分解为M=U·Σ·V*，那么矩阵M的逆矩阵为

M=V·Σ-1·U*

(9)

式中，Σ-1是Σ的逆矩阵，可通过矩阵Σ中主对角线上非零元素都求倒之后再转置得到。

1.3 Cholesky分解求逆

Cholesky分解求逆是指将一个正定的埃尔米特矩阵，即正定对称矩阵分解成一个下三角矩阵与其共轭转置之乘积。通过计算下三角矩阵的逆矩阵，快速求解正定对称阵的逆矩阵[18]。这种分解方式在提高代数运算效率、蒙特卡罗方法等场合中十分有用。实际应用中，Cholesky分解求逆在求解线性方程组中的效率约为三角分解求逆的两倍。

对于n×n的对称正定矩阵A，则存在一个主对角线元素严格正定的下三角矩阵L，满足

A=L·L*

(10)

式中：L是一个下三角矩阵且所有对角线元素均为正实数；L*是矩阵L的共轭转置矩阵。每一对称正定矩阵都有一个唯一的Cholesky分解过程。Cholesky分解的计算时间复杂度为O(n3/3)，正定对称阵A的逆矩阵可由下三角矩阵求逆确定，表示为

A-1=(L·L*)-1=(L-1)*·L-1

(11)

L是通过Cholesky分解得到的下三角阵，假设P是L的逆矩阵，则有

L·P=

(12)

由式(12)可知，P也是下三角矩阵，其中主对角线的值为

(13)

矩阵P是下三角矩阵L的逆矩阵，因此，矩阵A经过Cholesky分解后的逆矩阵为

A-1=(L·L*)-1=P*·P

(14)

2 精密单点定位

PPP是一种使用单个接收机的单系统伪距和载波相位观测数据，采用事后的精密卫星轨道和钟差产品，通过修正观测方程中的系统误差源获取高精度接收机坐标、接收机钟差、大气延迟和浮点模糊度的卫星定位方法。PPP不需要建立同步参考站，能够独立完成高精度绝对定位。同时，可以计算接收机钟差和大气延迟量，在科研和工程领域都具有较高的应用价值，也是目前GNSS数据处理领域的研究热点之一。

2.1 观测方程

采用无电离层组合观测方程[3]，包括无电离层伪距观测方程和无电离层载波相位观测方程，其表达式分别为

(15)

(16)

(17)

其中，

(18)

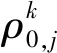
(19)

无电离层相位组合中的模糊度参数是宽巷模糊度和窄巷模糊度的组合，并且包含硬件延迟。因此，其不具备整数特性，在参数估计时需当作浮点数进行处理。在参数估计前需要对无电离层组合观测量进行系统误差修正，包括对流层延迟干分量、接收机端和卫星端的天线相位中心偏差(Phase Center Offset,PCO)和天线相位中心变化(Phase Center Variation,PCV)修正、相对论效应修正、相位缠绕误差修正、地球自转修正、固体潮修正、海潮修正和极移潮修正等。

对无电离层组合进行几何距离线性展开、斜向对流层延迟投影到天顶方向和系统误差修正处理后，将观测方程按照矩阵形式表达。若某一时刻有m个观测卫星，未知参数X的表达形式为

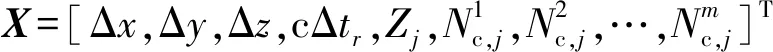
(20)

函数模型和随机模型统称为PPP数学模型，表达式分别为

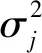
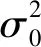
根据无电离层组合的表达式和误差传播定律，天顶方向相位无电离层组合先验精度约为1 cm，伪距无电离层组合先验精度约为1 m。斜向观测值精度与高度角有关，高度角越小先验误差越大，对应的权重也就越小。

2.2 参数估计

卡尔曼滤波是一种最优化的自回归参数估计算法，其基于一组观测序列以及动力学模型信息，采用递归算法求解状态向量的最优估值[19]。状态方程式和观测方程式的数学模型分别为

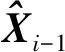
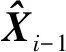
其中，

卡尔曼滤波算法将时间更新和观测更新依次迭代运行，就能够得到所有历元当前时刻的参数估值，是一种局部最优解。有别于最小二乘算法，卡尔曼滤波算法不需要存储所有观测时刻的数据，仅在当前历元进行状态预测和参数估计，未知参数相对较少，很大程度上节省了计算机内存并提高计算效率。另外，状态方程能够基于之前历元的参数估值预测下个历元的参数值，适用于未知参数随时间变化的观测方程。

3 实验分析

国际GNSS监测评估系统(International GNSS Monitoring and Assessment System,iGMAS)是对GNSS运行状况和主要指标进行监测和评估，生成高精度星历、钟差和全球电离层延迟模型等产品的平台。目前，由30个跟踪站、3个数据中心、7个分析中心、2个监测评估中心、1个产品综合与服务中心、1个运行管理控制中心和通信网络组成[20-22]。iGMAS跟踪站完成北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)、全球定位系统(Global Positioning System，GPS)、全球卫星导航系统(Global Navigation Satellite System，GLONASS)和Galileo等GNSS的信号接收和测量、原始观测数据的采集，并进行数据合理性检验和数据预处理，并将数据发送至数据中心备份。中国电子科技集团公司第五十四研究所长期稳定运行一个监测评估中心，研发多频多系统GNSS监测接收机，并装配16个iGMAS跟踪站，iGMAS跟踪站名称及全球分布情况如表1所示。

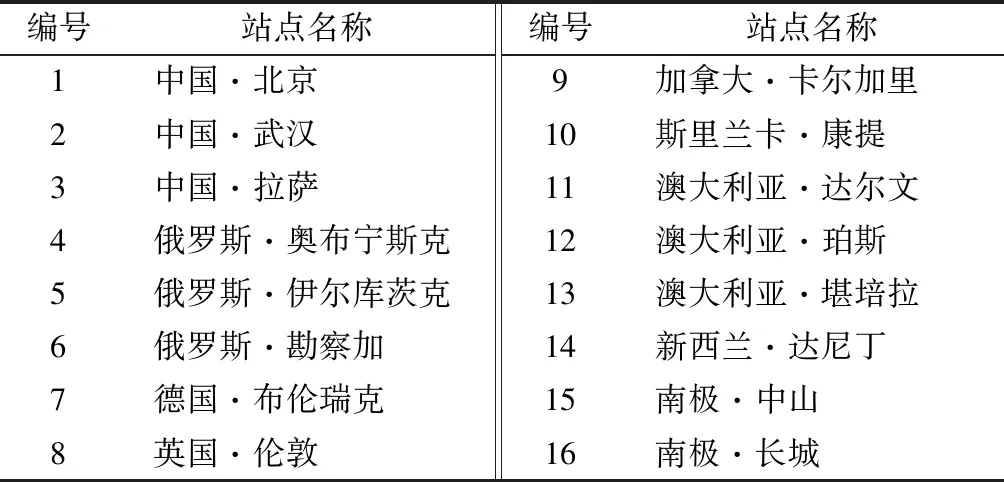
表1 iGMAS跟踪站名称及全球分布

为了分析不同矩阵求逆方法在GNSS精密单点定位参数估计中的应用效果，采用iGMAS跟踪站中的BJF1站在2020年第96天的北斗三号和北斗二号观测数据，进行PPP数据处理验证和处理性能分析。BJF1站位于北京，经纬度为39.6 °N和115.9 °E，接收机主机类型为CETC-54-GMR-4016，接收机天线类型为LEIAR25.R4。数据处理平台为联想E580 PC机，处理器为Intel Core i5-8250 U，主频为1.6 GHz。数据处理软件是在开源库GPSTk基础上开发的GNSS Data Processor软件。在动态PPP数据处理实验中，将接收机坐标参数作为白噪声进行估计。

PPP数据处理流程主要包括数据准备、数据预处理和参数估计。准备的数据文件包括精密星历文件和观测文件，其中精密星历文件可以通过FTP协议从IGS网站获取。将星历数据文件转换为SP3标准格式，观测数据文件转换为RINEX标准格式，完成数据准备工作。数据预处理主要包括周跳探测、粗差处理和误差源模型化修正。采用TurboEdit方法对周跳进行探测[23]，出现周跳的相位观测值通过调整权重进行处理，使用经验模型分别修正，包括卫星天线和接收机天线误差、相对论效应、相位缠绕误差、地球自转、固体潮、海潮和极潮等误差。参数估计部分包括建立函数模型和随机模型，并采用卡尔曼滤波算法依次对每个历元的观测值进行参数估计。卡尔曼滤波与权函数调整迭代运行，直到所有粗差被处理完成为止。

接下来分析SVD分解求逆与Choleskey分解求逆的计算速度。分别采用以上这两种方案处理BJF1站同一天的观测数据。在方案1中，采用SVD分解法处理PPP卡尔曼滤波中法方程求逆问题。在方案2中，则使用Choleskey分解法，求解相应的逆矩阵。统计两种方案中每个历元所需要的时间，包括读取文件、数据预处理和矩阵运算，其中矩阵求逆是主要项。两种方案的计算时间分别如图1和图2所示。

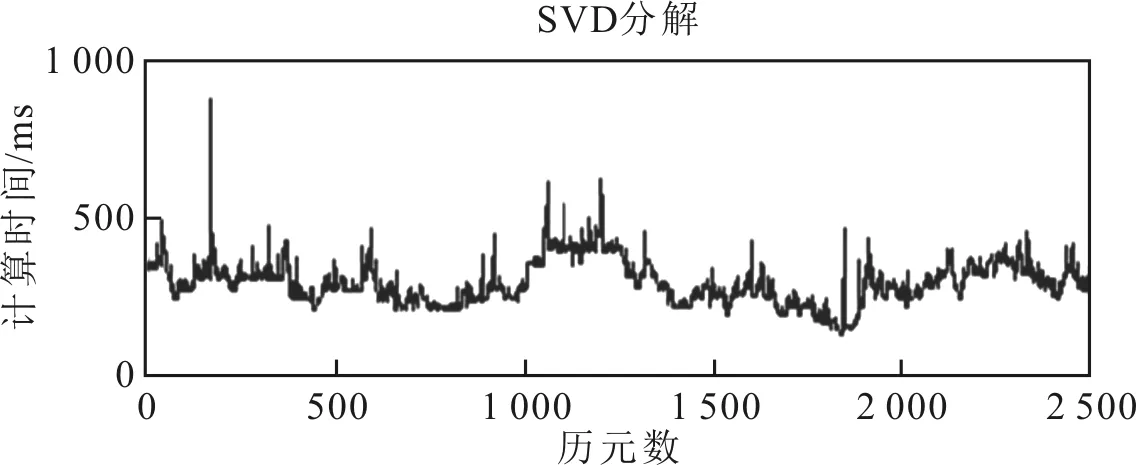
图1 动态PPP卡尔曼滤波法方程SVD分解求逆计算时间

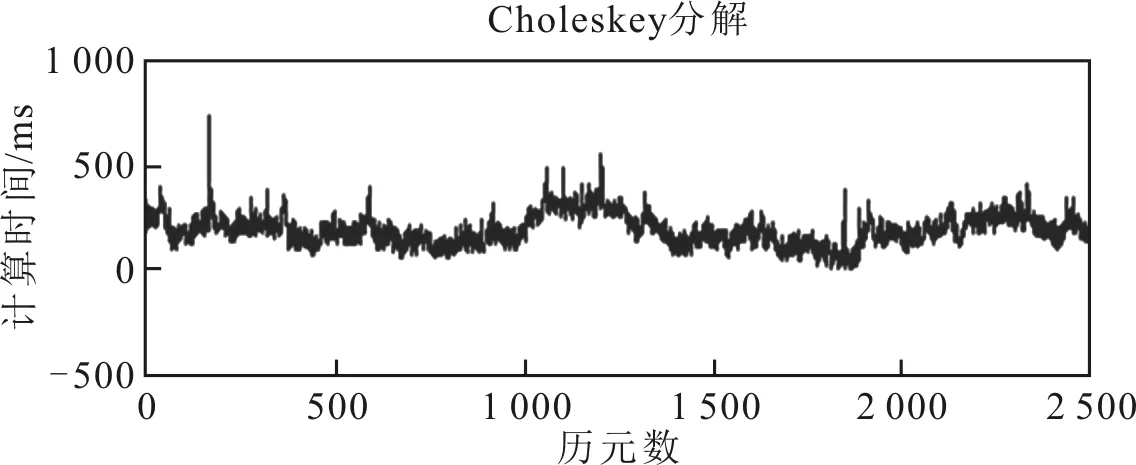
图2 动态PPP卡尔曼滤波法方程Cholesky分解求逆计算时间

由图1和图2可知，在一天所处理的2 500个观测历元中，SVD分解法所需计算时间变化较大，均值为291 ms。而Cholesky分解法所需时间比较稳定，均值为189 ms。两种方案均在第188个历元所需时间较长，通过处理日志判断该历元观测值粗差较多，需要多次矩阵求逆运算，导致该历元计算所需时间较长。

不同的矩阵分解方法求逆精度不一致，这会通过卡尔曼滤波参数估计从而影响PPP定位结果。分别分析SVD分解求逆法和Cholesky分解求逆法对BJF1站PPP定位结果的影响，对比分析方案1和方案2中BJF1站定位精度。以采用事后精密星历，静态PPP处理模式得到的BJF1坐标为参考值，将方案1和方案2中的定位结果分别与参考值进行对比，并将位置定位偏差转换到北方向(North,N)、东方向(East,E)、垂向(Up,U)方向，结果分别如图3和图4所示。

图3 动态PPP卡尔曼滤波SVD分解求逆定位结果

图4 动态PPP卡尔曼滤波Cholesky分解求逆定位结果

在采用SVD分解求逆法的方案1所中，BJF1站动态PPP定位偏差在45 min后首次收敛到0.2 m以内，并在之后的时间段内变化较大，尤其是U方向，抖动剧烈。而在使用Choleskey分解法求逆的方案2中，BJF1站动态PPP定位偏差在12 min就收敛到 0.2 m以内，整个时间段内的定位偏差也表现稳定。经统计，采用SVD分解法的动态PPP在N、E、U三维方向的定位精度分别为5.95 cm、8.04 cm、20.31 cm，而使用Cholesky分解法的定位精度则分别是2.65 cm、4.05 cm、8.04 cm。

由此可知，无论是在计算所需时间方面，还是在因矩阵求逆误差而导致的定位偏差方面，Cholesky分解法均优于SVD分解法，具体的SVD分解和Cholesky分解效果对比情况如表2所示。

表2 SVD分解和Cholesky分解效果对比

4 结语

矩阵分解求逆在工程应用中具有重要价值。论述了矩阵求逆的基本理论和方法，介绍矩阵广义逆的性质及其在线性方程解中的作用。重点论述了两种矩阵分解求逆方法，包括SVD分解求逆法和Cholesky分解求逆法。其中，SVD分解法可用于求解广义逆和方阵求逆，而Cholesky分解法适用于正定对称矩阵求逆。精密单点定位是一种GNSS高精度定位算法，参数估计是PPP数据处理的重要环节，可通过矩阵分解进行快速求逆运算。描述了PPP算法观测方程，介绍观测方程中各参数的几何和物理含义，包括各种误差项的具体处理策略，并论述一种卡尔曼滤波参数估计算法。

采用iGMAS中的BJF1站北斗二号和北斗三号观测数据进行PPP处理，验证SVD分解法和Cholesky分解法的矩阵求逆效果。基于SVD分解法的动态PPP每个历元数据处理所需时间均值为291 ms，N、E、U三维方向定位误差分别为5.95 cm、8.04 cm、20.31 cm。使用Cholesky分解法的动态PPP每个历元数据处理所需时间为189 ms，三维方向定位误差分别为2.65 cm、4.05 cm、8.04 cm。因此，相比于SVD分解法，Cholesky分解法应用于矩阵求逆的时效性更好，动态定位精度统计结果也间接证明了Cholesky分解法矩阵求逆精度更高。这是因为PPP卡尔曼滤波法方程为对称正定矩阵，在矩阵求逆时Cholesky分解法更为适用。