双耦合极化码及其编码调制方案

陈皓炜，蔡穗华，韦宝典，马 啸

（中山大学计算机学院，广东广州 510006）

1 引言

极化（Polar）码是E Arikan 于2008 年基于信道极化现象提出的一类线性分组码［1，2］，是首个可理论证明能达到任意二进制输入离散无记忆对称信道（Binary-Input Discrete Memoryless Channels，BI-DMC）容量且具有较低的编译码复杂度和确定性构造的信道编码方案，因而近年来广受关注.E Arikan 针对所提出的极化码设计了逐次抵消（Successive Cancellation，SC）译码算法［2］以及置信传播（Belief Propagation，BP）译码算法［3］.SC 译码算法在中短码长下性能较差，于是有研究者提出了逐次抵消列表（Successive Cancellation List，SCL）译码算法［4～6］和逐次抵消堆栈（Successive Cancellation Stack，SCS）译码算法［7］.BP 算法由于性能较差，并且高信噪比下会出现错误平层，其他研究者提出了软抵消（Soft Cancellation，SCAN）译码算法［8］和置信传播列表（Belief Propagation List，BPL）译码算法［9］.

为了进一步提升极化码的纠错性能，学者们提出了级联极化码，即在极化码编码器外级联一个系统外码.典型的级联极化码有循环冗余校验（Cyclic Redundancy Check，CRC）辅助的CA-Polar 码［4，10］和基于奇偶校验（Parity Check，PC）的PC-Polar码［11］.2019年，E Arikan 提出了卷积极化码（Polarization-Adjusted Convolutional Codes，PAC）［12］，用码率为1 的卷积码代替级联外码.此外，文献［13］提出了一种基于空间耦合（Spatial Coupling，SC）的SC-Polar 码，可以进一步提升极化码的纠错性能.

为满足日益增长的数据速率需求，通信系统常常通过编码调制来达到较高的频谱效率.极化码在加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道下具有优秀的纠错性能，于是研究者们将极化码与高阶调制相结合以实现高谱效、高能效的信息传输.典型的编码调制方案主要有比特交织编码调制方案（Bit-Interleaved Coded Modulation，BICM）［14，15］和多层编码调制方案（Multilevel Coding，MLC）［16］.2013 年，M Seidl 等人将二元极化码与BICM和MLC相结合，提出了基于极化码的编码调制方案［17］，即比特交织极化编码调制（Bit-Interleaved Polar Coded Modulation，BIPCM）和多层极化编码调制（Multilevel Polar Coding，MLPC）.

在码长较短的情况下，为了提升极化码的性能，我们结合双向叠加传输（Twisted-Pair Superposition Transmission，TPST）方案［18］和SC-Polar 编码方案，提出了双耦合极化码（Dual Coupled Polar，DC-Polar）编码方案［19］并推导了其性能下界.在高阶调制下，我们给出了采用双耦合极化码的BICM 方案，但由于其存在码长匹配的问题，我们基于MLC 的思想设计了双层耦合极化编码调制（DC-Polar Two-Layer Coding，DC-Polar-TLC）方案，该方案使用两个编码器，可以根据调制阶数灵活地分配码长.本文以16QAM和64QAM 下的DC-Polar-TLC系统为例进行仿真，结果表明，在64QAM 调制下，该方案与使用BICM系统的CA-Polar码相比具有约0.6 dB的增益.

2 双耦合极化码

2.1 极化码

信道极化的过程分为信道合并和信道分裂两个步骤.当码长N趋于无穷时，经过极化码编码后的等效比特子信道将极化成几乎无噪的（对应容量为1）或无用的（对应容量为0），其中长度为K的信息比特将在这些几乎无噪声的比特信道内传输，称这些比特信道的序号集合为信息位集合A；长度为N-K的固定比特（称为冻结比特）将放置在无用的比特信道上，称这些比特信道的序号集合为冻结位集合Ac，于是有A∪Ac={1，2，…，N}.我们在信道中传输了N个比特，其中包括K个信息比特，称这种从K维空间到N维空间的映射为极化码编码.

在本文中，我们采用记号Polar(N，K，)来表示一个极化码，其中N=2n表示极化码的码长，K表示信息序列长度，表示长度为N-K的冻结比特序列.

2.2 双耦合极化码编码

双耦合极化码［19］是一种将极化码作为成分码、采用上下两层结构来进行码率分配的编码方案，其上下层之间通过空间耦合进行连接，代替了TPST［18］方案的前向叠加步骤.其基本思想是，利用上下层进行联合编码从而获得性能增益.空间耦合技术将上层的信息处理后放入下层的冻结位上，因此上层的少量错误会带来下层的显著变化，从而使得上层的正确序列更容易被识别.后向叠加技术将下层叠加到上层，因此逐次抵消过程中，在给定上层的情况下，下层进行了部分重传，性能得到改善从而有利于正确码字的识别.为了改善上层的性能，我们使用具有较强纠错能力的列表译码来加大正确码字的影响，从而便于列表内正确码字的识别.

双耦合极化码的编码如图1所示，其编码过程是将长度为K=K0+K1的信息序列编码成长度为2N的码字.算法1 给出了具体的编码算法，其中，S是大小为K0×(N-K1)的耦合矩阵，用于提取上层的编码信息用作下层的冻结比特.Π 是大小为N×N的交织器.为简单起见，本文选择耦合矩阵S和交织器Π 为反向排序矩阵［19］.

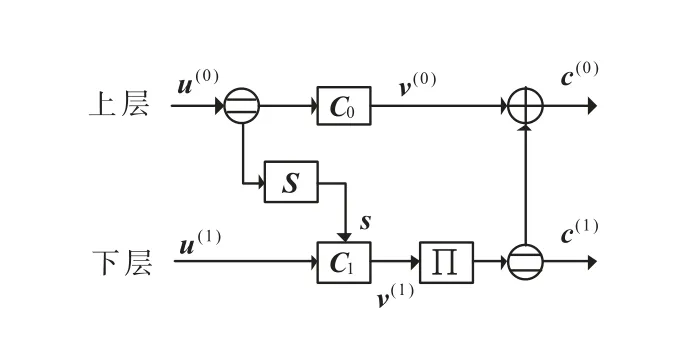
图1 双耦合极化码的编码框图

2.3 双耦合极化码译码

双耦合极化码的译码思路为：通过解调得到的概率序列y来计算上层的概率序列y(0)，并将结果y(0)送入上层子极化码的SCL 译码器中进行译码.将上层译码得到的信息序列进行重新耦合以及重新编码，其中重新耦合的结果作为下层译码器的冻结比特参与下层子极化码的SCL 译码，重新编码的结果用于计算下层概率序列y(1)，之后将结果y(1)送入下层子极化码的SCL 译码器中进行译码.将上下层的译码结果进行重编码，并计算码字似然值，取似然值最大的码字作为双耦合极化码的译码结果.

令P(y|c)表示在已知发送码字c的条件下，接收到y的概率，则双耦合极化码的逐次抵消列表译码算法如算法2所示.

2.4 性能下界

在本节中，我们根据精灵辅助（Genie-Aided，GA）等方法，分析了SCL译码器的误帧率（Frame Error Rate，FER）FERSCL，因此性能下界可推导如下.

（1）上层精灵辅助界P(E0)

考虑事件E0表示v(0)不在上层候选码字列表.我们把下层往上的叠加看成是在上层中加入了噪声，这样概率序列y(0)就可以看成是v(0)经过二元干扰AWGN信道后的输出，其中边信息为y(1).将y(0)送入译码器中进行译码，并在译码中加入精灵辅助，即一旦候选码字中有正确的码字，则将正确的码字输出，我们将上层SCL译码器的性能当作P(E0)的估计值.

（2）下层精灵辅助界P(E1)

考虑事件E1表示在v(0)已知的情况下，下层译码器输出的结果不是v(1).在上层已知的情况下，向上叠加后发送相当于下层码字发送了两次.我们将下层SCL 译码器的性能当作P(E1)的估计值.

由上分析可以得出精灵辅助下界为

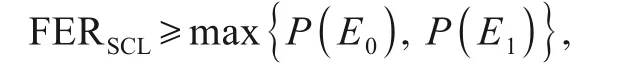
于是我们便可以通过选择子极化码的参数来使得下界达到最小.

示例1为了构造码长为64，信息序列长度为K0+K1=32 的双耦合极化码，我们将上下层的子极化码码长设置为32，均采用SCL 译码器，最大列表大小分别为32和8.图2 所示为不同信息长度分配(K0，K1)下的精灵辅助界.在误帧率为10-5附近，我们选择上下层信息长度分配为(14，18)的参数构造双耦合极化码，因为在这种情况下，其精灵辅助下界在比较大的范围内是最优的，即max{P(E0)，P(E1)}在这种情况下是最小的.

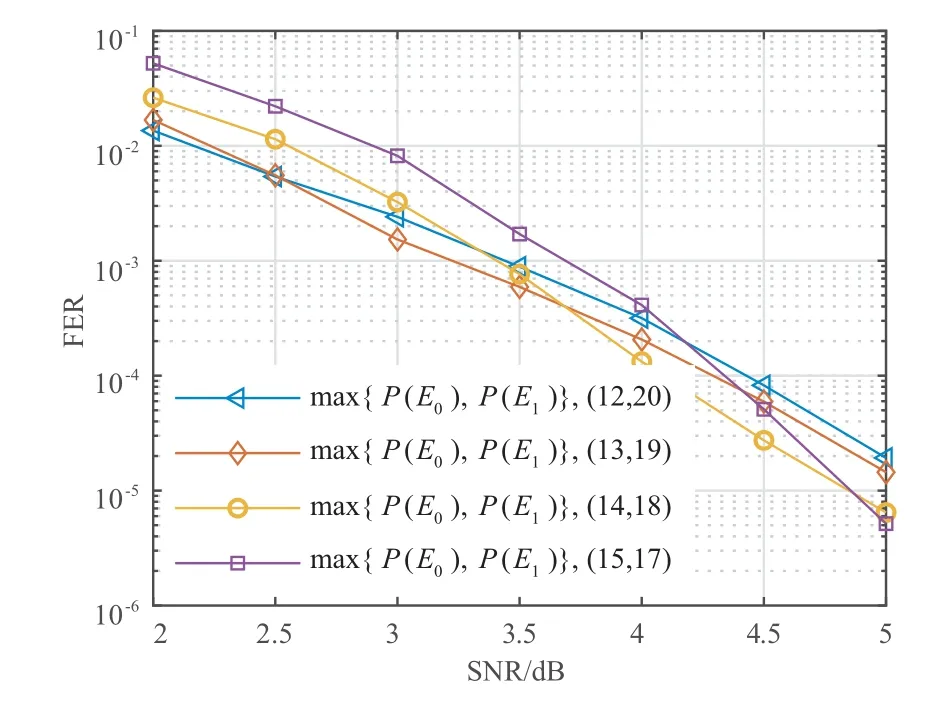
图2 双耦合极化码在不同参数(K0，K1)构造下的精灵辅助界

图3给出了BPSK调制下双耦合极化码在不同参数(K0，K1)构造下的性能.同时，我们也给出了参数(14，18)下的GA 下界以及最大似然（Maximum Likelihood，ML）下界的曲线.我们可以看出在5 dB 附近，使用参数(14，18)构造的双耦合极化码的性能是最优的.这证实了我们从精灵辅助下界中得出的结论.

图3 双耦合极化码在不同参数(K0，K1)构造下的性能及其界

图4 所示为双耦合极化码和CA-Polar 码［4，10］以及PAC［12］在码长为64，不同码率下的性能.可以看出，所提出的双耦合极化码具有良好的性能，在不同码率下性能都与现有极化码短码构造性能相当.

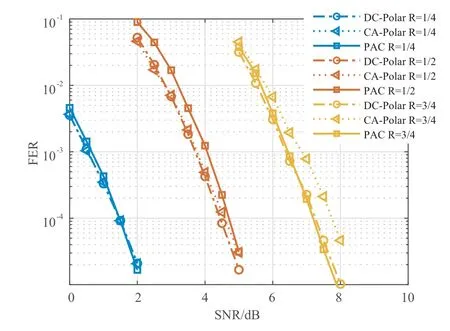
图4 双耦合极化码与其他码的性能比较

3 双耦合极化码的高阶调制

在此节中，我们介绍高阶调制下的双耦合极化码，并给出其相应的编码调制方案.

3.1 双耦合极化码的比特交织编码调制

由于极化码的码长必须为2的幂次，因此当高阶调制映射的比特数不是2 的幂次时，比特交织编码调制（BICM）系统会存在码长匹配的问题.码长匹配的常用方法是删余或截短［20］，其中删余方法有准均匀删余（Quasi-Uniform Puncturing，QUP）［21］及其扩展算法［22］，在本文中仅使用QUP 算法，并将删余后的传输长度记为M.双耦合极化码的BICM 系统框图如图5 所示，在双耦合极化码编码完成之后，将码字c=(c(0)，c(1))送入交织器以及映射器中，经过格雷（Gray）映射得到已调符号序列x.信号经过信道之后，先解映射成概率序列y，之后再解交织，最后送入双耦合极化码的译码器中进行译码.

图5 双耦合极化码的BICM系统框架

示例2在16QAM 调制下，我们考虑码长为128，信息序列长度为K0+K1=64 的双耦合极化码.上下层的子极化码码长设置为64，均采用SCL 译码器，最大列表大小分别为128和8.图6 所示为不同信息长度分配(K0，K1)下的精灵辅助界.可以看出在误帧率为10-5附近，参数(23，41)的精灵辅助界是最优的，因此我们使用该参数来构造双耦合极化码.

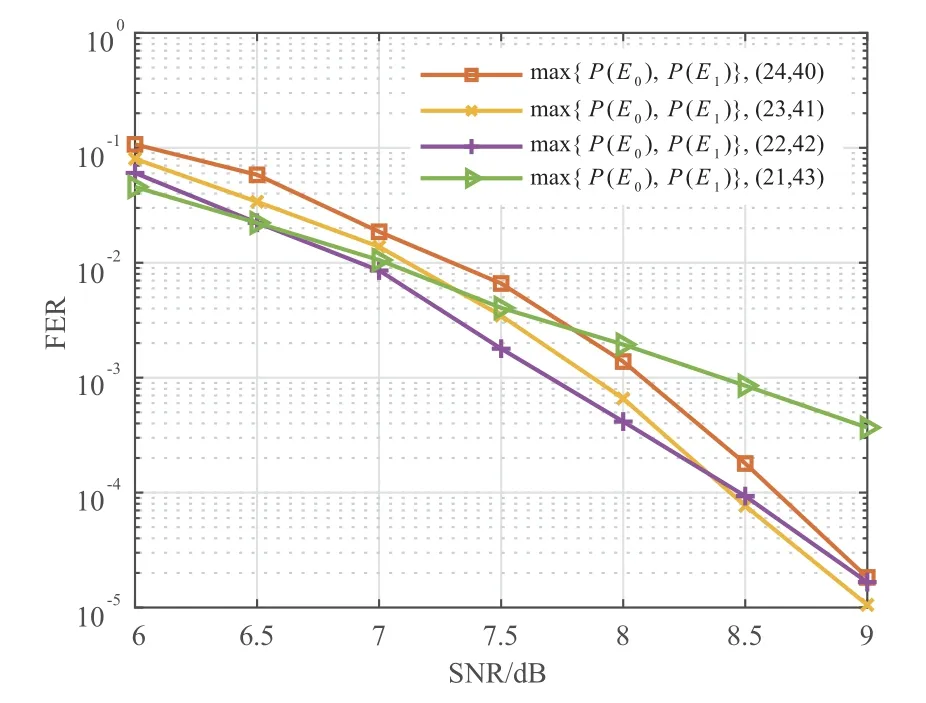
图6 16QAM 调制下BICM 系统中双耦合极化码在不同参数(K0，K1)构造下的精灵辅助界

简单起见，BICM 系统中的交织器设置为随机交织器.我们在图7 中给出了文献［23］中的PAC 以及［24］中的CA-Polar码在BICM系统中16QAM调制下的性能，与双耦合极化码的性能进行对比.可以看出双耦合极化码的性能处于PAC和CA-Polar码之间.

图7 16QAM 调制下BICM 系统中双耦合极化码在参数(23，41)构造下的性能及其界,其中PAC和CA-Polar 码均由参数N=128,K=64构造,SCL译码器参数为L=128

示例3在64QAM调制下，我们考虑码长为192，信息序列长度为K0+K1=96的双耦合极化码.上下层子极化码的母码长度设置为128，传输长度为96.图8所示为不同信息长度分配(K0，K1)下的精灵辅助界.可以看出，在误帧率为10-4附近，参数(34，62)的精灵辅助界是最优的，因此我们使用该参数来构造双耦合极化码.

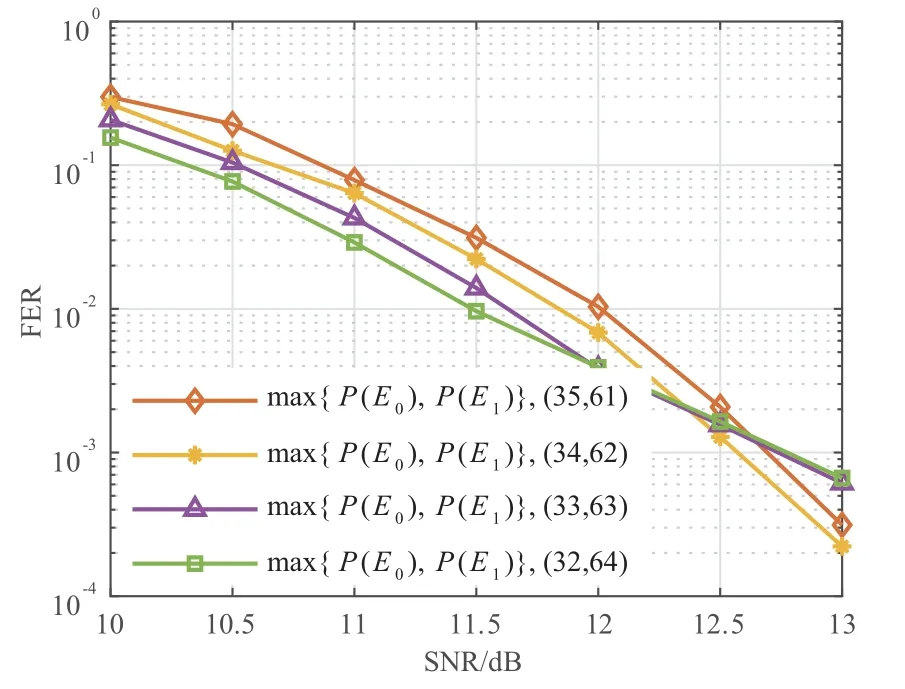
图8 64QAM 调制下BICM 系统中双耦合极化码在不同参数(K0，K1)构造下的精灵辅助界

同样地，我们在图9 中给出了CA-Polar 码在BICM系统64QAM 调制下的性能，与双耦合极化码的性能进行对比.由图可以看出，在64QAM 调制下，删余操作对双耦合极化码性能的影响会更大一些.因此，我们需要考虑一种码长更为灵活，不需要进行删余或截短操作的编码调制方案.

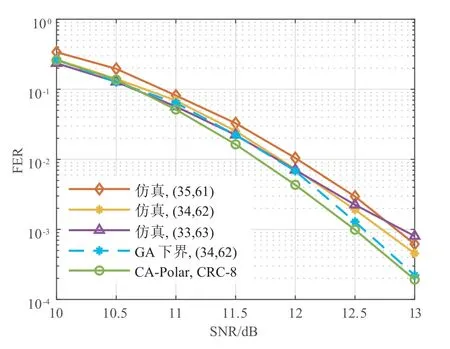
图9 64QAM 调制下BICM 系统中双耦合极化码在不同参数(K0，K1)构造下的性能及其界,其中CA-Polar 码由参数N=256,M=192,K=96 构造,SCL 译码器参数为L=128,CRC 生成多项式为g(x)=x8+x5+x4+1

3.2 双层耦合极化编码调制

为了构造出码长灵活的双耦合极化码，我们基于多层编码调制（MLC）的思想，提出了双层耦合极化编码调制（DC-Polar-TLC）方案.其基本思想是，利用子集划分（Set Partition，SP）映射［25］代替后向叠加.此时，与后向叠加类似，在逐次抵消过程中，当上层的映射比特给定时，下层的星座点具有较大的距离，从而能够改善下层的性能.这样做的好处是，在高阶调制下可以将SP映射和编码联合设计，从而解决码长匹配的问题.

DC-Polar-TLC方案的性能下界可推导如下.

（1）上层精灵辅助界P(E0)

在SP 映射下，我们采用上层对应比特的软信息作为输入，送入上层译码器进行译码，从而得到上层的译码误帧率性能.因为使用了SP 映射，相邻星座点间可能有多个比特存在差异，因此相比于Gray 映射，上层的译码性能会有所下降.

（2）下层精灵辅助界P(E1)

在上层比特已知的条件下，我们提取下层比特软信息，送入下层译码器进行译码，得到精灵辅助下的下层误帧率性能.得益于SP 映射方式，在上层比特已知时，剩余比特对应的星座点之间具有较大的距离，相比于Gray映射，下层的译码性能会有所改善.

和双耦合极化码类似，我们可以通过选择子极化码的参数来使得下界达到最小.

值得指出的是，双耦合极化码的后向叠加是在二元域上进行加法运算，而DC-Polar-TLC 方案借助的是SP映射和MLC方案，其增益和星座的选择与划分有关，因此需要针对具体的星座进行优化设计.

本文以16QAM和64QAM 的DC-Polar-TLC 系统为例进行说明.

在16QAM 调制下，DC-Polar-TLC 系统框图如图10所示.上下层采用码长相同的子极化码进行编码，编码完成之后进行交织并分段，最后送入映射器中进行映射.需要说明的是，DC-Polar-TLC 系统通过SP 映射划分出两层，每层分成两路序列并采用Gray映射.

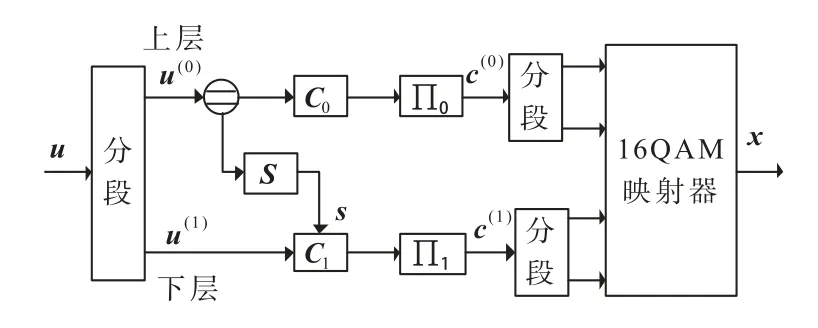
图10 16QAM调制下的DC-Polar-TLC系统框架

在64QAM 调制下，DC-Polar-TLC 系统框图如图11所示.上下层采用码长不同的子极化码进行编码，令N0表示上层子极化码的码长，N1表示下层子极化码的码长.根据映射方式不同可以分成两种情况.第一种情况是N0=2N1，其中上层对应星座的前四个比特，下层对应星座的后两个比特，称这种映射方式为Φ1，如图11（a）所示.第二种情况是N1=2N0，其中上层对应星座的前两个比特，下层对应星座的后四个比特，称这种映射方式为Φ2，如图11（b）所示.

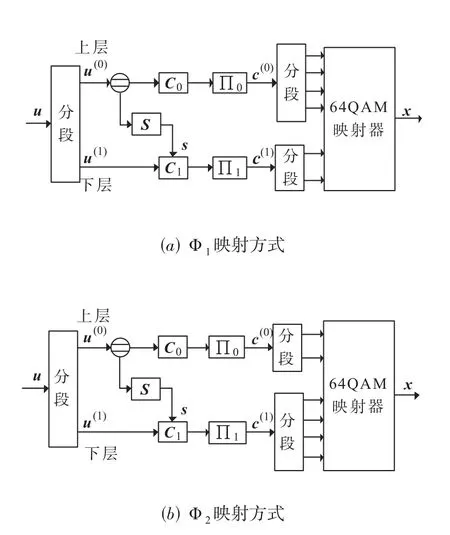
图11 64QAM调制下的DC-Polar-TLC系统框架

示例4在16QAM 调制下，我们考虑整体码长为128，信息序列长度为K0+K1=64 的DC-Polar-TLC 系统.令上下层子极化码的长度为64，均采用SCL 译码器，最大列表大小分别为128和8.经过测试，我们使用参数(19，45)进行构造.

图12 给出了DC-Polar-TLC 系统与三种不同码在BICM 系统下的性能对比.可以看出，在16QAM 调制下，BICM系统的性能要略优于DC-Polar-TLC系统.

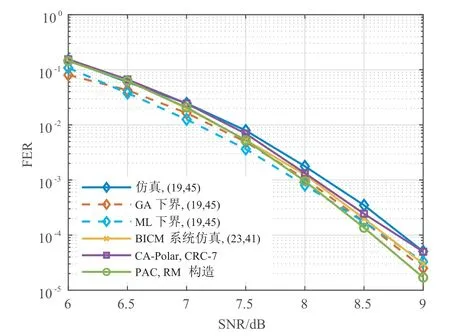
图12 16QAM 调制下DC-Polar-TLC 系统在参数(19，45)构造下的性能及其界

示例5在64QAM 调制下，我们考虑整体码长为N0+N1=192，信息序列长度为K0+K1=96 的DC-Polar-TLC 系统.经过测试，在Φ1映射下我们使用参数(39，57)进行构造，在Φ2映射下我们使用参数(8，88)进行构造.

图13 所示为64QAM 调制下BICM 系统、DC-Polar-TLC 系统、正态近似（Normal Approximation，NA）界［26］以及文献［27］中的延时BICM（Delayed BICM，D-BICM）系统的性能比较.可以看出，在64QAM 调制下，DC-Polar-TLC 系统的性能超过了BICM 系统中的双耦合极化码和CA-Polar 码的性能，以及D-BICM 系统中极化码的性能.这是因为BICM 系统在64QAM 调制下需要进行删余或截短等码长匹配的操作，在一定程度上会影响性能，而DC-Polar-TLC 系统可以灵活地分配上下层码长，因此不会有性能损失.

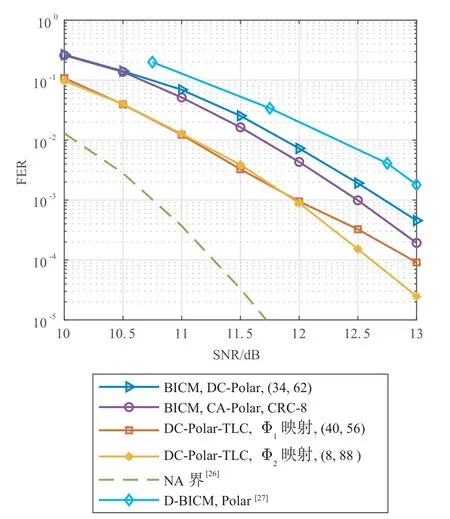
图13 64QAM调制下BICM系统和DC-Polar-TLC系统性能比较

4 结论

本文提出了高阶调制下双耦合极化码的编码调制方案，并根据最优的精灵辅助下界来选择参数进行构造.为了得到码长灵活可变的双耦合极化码，本文提出了双层耦合极化编码调制（DC-Polar-TLC）方案，并分析了DC-Polar-TLC 方案与BICM 方案的区别，通过仿真验证了DC-Polar-TLC 方案的效果比使用删余的BICM 方案更好.本文还举例说明了64QAM 调制下DC-Polar-TLC 方案的两种不同映射的区别，通过仿真发现Φ2映射方式的性能比Φ1映射方式的更好.仿真表明，Φ2映射方式下DC-Polar-TLC 方案的性能比使用BICM 方案的CA-Polar码提升了约0.6 dB.