问题设定驱动的深度强化学习研究:综述
张政锋 赵彬琦 单洪明 张军平
强化学习(Reinforcement Learning, RL)[1]常指智能体通过充当交互接口的马尔科夫决策过程(Markov Decision Process, MDP)[2]在真实环境学习最优策略的序列决策问题.近年来,结合深度神经网络强大表征能力的深度强化学习(Deep RL)在MDP方面具备更好地描述复杂任务场景的能力.具体而言,基于交互接口MDP的智能体,深度强化学习在环境反馈中获取交互经验,通过优化基于期望回报的学习目标,获得最优策略.深度强化学习能为灵活多样的任务场景提供以学习算法为主的解决方案,在棋类[3]、游戏[4]、核聚变[5]等多领域均形成突破性的进展.
强化学习的主流分类方法以马尔可夫决策过程为基础,以单智能体与多智能体为两条主线,根据任务类型的难点所在划分多样的研究方向[6].例如,针对一些任务无法定义收益函数(Reward Function)的难点,发展一系列的逆强化学习方法.这种主流分类方法有助于理论研究者集中精力解决某一核心难点并提供理论保证,但从一类技术方法本身出发探究其适用的问题,对应用研究者而言显得过于分散.而且现实场景总是夹杂多个难点,侧重于单一难点的技术方法在具体问题场景中的效果并不理想.因此,采用问题设定的分类法,以一个问题自身为驱动,将任务设定与解决方案追求的问题特性归纳为考量因素,能为强化学习的发展提供更统一的综述视角.
具体而言,任务设定是对问题场景固有限制的描述,如该设定下动作空间是离散或连续、环境是否具备重置回任一状态的功能.而问题特性指在任务设定的限制下解决方案追求的特性,如有效性、安全性、灵活性等.例如,机器人领域的技术方法除了保证有效性以外,对安全性与实用性提出更高要求,而游戏领域更倾向于灵活性,如策略类型是选择平稳性或非平稳性、是否显式参数化策略函数等,并且解决方案追求问题特性的不同会显著影响算法性能.因此,任务设定与问题特性是当前众多算法发展的根源性差异,这两者统称为问题设定,并以此为新的视角,可为强化学习的发展提供问题设定驱动的研究综述.
当前深度强化学习方面的研究综述主要围绕在其特定研究分支的技术方法和与不同交叉领域的联系上.具体地,高阳等[7]介绍强化学习的基本原理与算法,分析多智能体相关算法.刘全等[8]从值函数、策略梯度、搜索与监督的角度阐述当前深度强化学习的主要方法,从分层、多任务、多智能体、记忆与推理四方面进行梳理.孙世光等[9]综述基于模型的强化学习在机器人场景下的具体模型与方法.Levine等[10]对离线强化学习进行详尽的研究综述.Sutton等[1]具体介绍强化学习的起源、历史、基础技术和多学科领域的联系,如心理学、神经科学等.Bertsekas等[11]深刻揭示强化学习与最优控制领域的内在联系.除此以外,还有众多对强化学习特定分支的研究综述,如分层强化学习[12]、元强化学习[13]等.
不同于先前综述的分类方式,本文以问题设定(任务设定与问题特性)为视角,从智能体、任务、MDP、策略类型、学习目标、交互模式六大设定对象挖掘强化学习不同研究方向的内在关联性,为应用研究者提供更符合现实场景的综述视角.整体而言,从问题特性和任务设定两个因素,分析强化学习的核心挑战,再阐述问题设定的形式化定义,然后以基础设定的变更为前提,深入分析不同算法的根源性差异,探讨其特点、适用性及局限性,最后展望潜在的发展方向.
1 强化学习问题的核心挑战
强化学习方法在不同设定下的有效性主要面临两大核心挑战:效用分配(Credit Assignment)和探索与利用(Exploration-Exploitation).其源于两条相互交错的发展主线——最优控制与试错学习,分别受问题特性与任务设定的影响.最优控制主要贡献价值函数和贝尔曼方程用于效用分配,有“延迟收益”(Delayed Rewards)的特点.试错学习主要贡献策略搜索,在探索过程中有“试错(Trial-and-Error)”的特点.
1.1 面向问题特性的效用分配
效用分配是关于如何将延迟的收益信号分配到恰当状态或状态-动作对上的挑战,有“延迟收益”的特点,反映分配过程要达到何种“结果”,侧重于问题特性.
早期,Minsky[14]提出效用分配的形式化定义,从时序与结构化这两个阶段定义效用分配的基本MDP.1984年,Sutton[15]对表格型的任务设定进行初步描述与研究,认为由收益函数决定的价值函数是极其重要的,依据是价值函数决定了状态-动作对的长期回报,并为智能体的行为模式,即策略函数,提供了决策依据,起着“效用分配”的关键作用.因此,隐式评估策略价值函数的准确估计是首要的,是算法有效性的主要研究思路,称为策略评估(Policy Evaluation).这一核心观点极大推动基于价值的深度强化学习方法的发展,如使用蒙特卡洛或时序差分(Temporal Difference, TD)等方法估计价值函数.该研究思路与最优控制的基础定义高度相似[11],在一定约束条件与效用函数下,规划一种控制策略,使系统的某个性能指标最大.早期强化学习对效用分配的研究结合最优控制中的贝尔曼方程,精确求解最优策略,适用于简单的表格型任务.特别地,最优控制方法更强调基于精确、已知的环境动力学的规划过程,而强化学习方法更注重从环境“交互”中的试错学习过程.
随着2012年深度神经网络在图像识别领域以里程碑的形式出现,其强大的表征能力进一步扩展隐式策略建模方法的应用边界.Mnih等[16]提出将深度神经网络与动作价值函数(Q-value)结合的DQN(DeepQ-learning Network),应用于具有高维连续状态、离散动作设定的雅塔利(Atari)游戏中.在未知环境动力学、无人工设计特征的任务设定下,单凭交互过程中的试错学习,首次验证方法在高维状态空间下的有效性.2016年,AlphaGo[3]考虑问题特性中的效率性,在DQN的基础上拓展任务设定,引入人类专家的示教数据,结合蒙特卡洛搜索方法的控制策略,击败当时的世界围棋冠军.后来,值方法在不同问题特性的考量下开始持续发展.
随后,Deepmind为了追求灵活性,在星际争霸游戏[4]中引入自我博弈的训练机制.在商业上,成功落地的国内腾讯公司的王者荣耀游戏AI[17]从策略鲁棒性的角度引入联盟训练(League Training).这些重大进展得益于游戏虚拟环境中训练样本低廉的获取方式.例如,王者荣耀游戏AI训练的基本资源单位需要用到320块GPU和35 000个CPU核,所需样本达到千万级别.然而,上述方法具有一定的局限性,在机器人领域面临高样本复杂度的难题.2018年,为了完成机械臂通过摄像头进行感知的抓取任务[18],大约需要58万次现实抓取的训练,智能体才能获取具有96%成功率的抓取策略,这在现实世界中对机械造成的耗损是难以接受的.
继而,现实任务场景对强化学习方法的实用性提出更高要求.在资源调度领域,2019年,滴滴出行公司利用值估计的诸多技术,如平滑版本的n步收益裁剪[19],成功在订单调度的现实任务上落地基于深度值网络的强化学习方法,在诸如最大化司机回报、订单响应时间等多项系统指标上超越原有产品的基线.在机器人领域,伯克利的AI研究中心采用从虚拟到现实的研究思路,利用更准确的价值估计算法——REDQ(Randomized Ensemble DoubleQ-learning)[20],在2021年以数万现实样本的代价实现四足机械狗在不同现实场景中的高质量走动[21].
1.2 面向任务设定的探索与利用
探索与利用是关于智能体如何从环境中高效收集与任务目标相关的收益信号的挑战,有“试错”的特点,反映如何找到效用分配过程要达到的“结果”,受任务设定的影响.早期,关于试错学习(Trial-and-Error Learning)的概念源于动物学习心理学领域,Thorndike[22]提出的“效应定律(Law of Effect)”,简明扼要地表明试错学习的本质是一种学习原则,并通过猫逃脱箱子实验中的本能行为,验证强化物(Reinforcement)对决策行为倾向性的影响.直观而言,猫的本能冲动产生试错行为(Exploratory Behavior),引出逃脱箱子的行为结果,通过某种方式连接行为的决策机理,验证试错行为的可学习性.1958年,Skinner[23]发表关于强化鸽子喙击木球这一行为模式的实验,揭示另一种学习原则,即“持续不断对理想行为模式进行强化可塑造行为的结果”.这类早期研究揭示智能体在某类强化物的刺激下会产生试探性行为,并从中学习理想行为模式的原则.
经过计算术语的转换,上述研究观点成为显示策略建模的强化学习方法背后的动机与原理.具体地,将策略指代为智能体当前的行为模式,探索视为智能体试探性的行为模式,利用视为智能体经过试错经验的学习过程后的行为模式,最优策略指代完成任务的理想行为模式.
探索与利用中最简化的任务设定可追溯到1933年只有一个状态的多臂老虎机问题(Multi-armed Bandits)[24].围绕着如何平衡探索与利用能使总体回报最大这一主题,经过数十年研究,已拥有相对成熟的研究体系.然而,多臂老虎机的序列长度为1,而强化学习是一个序列决策问题.在任务设定上,新增的序列特性意味着智能体需要学会忍受短期损失以换取长期回报的策略.
面对低维离散的任务设定,1990年,Sutton[25]提出解决随机游走问题的玻尔兹曼分布,其中的温度系数充当调节探索与利用之间平衡的作用.1992年,Williams[26]提出第一个基于策略梯度进行搜索的方法REINFORCE,引入新的设定对象——显式构建策略函数,调节训练过程中动作噪声的大小以平衡探索与利用.近年来,Haarnoja等[27]提出SAC(Soft Actor Critic),调节策略目标中以信息熵为代表的随机性以平衡两者之间的关系,将探索的有效性扩展到高维连续的任务设定类型上.考虑到设定中随机初始条件与稀疏收益信号导致的低探索效率,Le Paine等[28]提出R2D3(Recurrent Relay Dis-tributed DQN from Demonstrations),在半交互的任务设定下展开对专家数据辅助探索的研究,改善样本复杂度.相反地,离线强化学习为了避免高昂的探索成本,在零交互的设定上研究效用分配的问题,尽管其问题设定的更改决定算法性能的理论上限,却大幅增强相关方法的实用性.
尽管探索方法因任务设定而截然不同,但寻求尽可能有效、可泛化的探索原则是当今这类研究的主要方向.2021年,Ecoffet等[29]提出Go-Explore,揭示“返回可能存在高收益的情景,再进行随机性试探”的简单探索原则,大幅提高探索效率.此外,还有反映智能体内在行为动机(Intrinsic Motivation)以量化状态-动作空间的探索进度(Space Coverage)、乐观看待探索的不确定性和基于信息增益进行决策等探索原则[30].
2 基本定义
强化学习问题主要有3个实体对象:智能体、MDP、环境.具体地,智能体有策略、价值和交互经验池这3个基础对象.智能体与环境的交互接口MDP包含状态、动作、收益、环境动力学、折扣因子这5个元素,用于准确描述环境中的任务.具体关系图如图1所示.
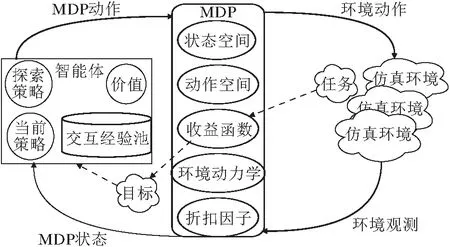
图1 强化学习问题的关系图
强化学习问题的MDP定义为
M=(S,A,R,P,γ).
首先,使用离散的时间序列[2]描述MDP,时间变量为t,幕(Episode)的长度为T;在每个时间刻t∈T,智能体接收用于描述环境观测的状态变量为St,其值s来自MDP中的状态空间S,At表示动作变量,其值a来自MDP中的动作空间A,策略为π(At|St).然后,定义P为环境动力学的函数集合,R为收益函数集合,环境动力学为P(St+1|St,At),其中P∈P,返回下一状态值s′及收益信号R(St,At,St+1),简记为Rt,R∈R.当智能体碰到终止状态ST,将轨迹形式的样本
τ=(S0,A0,R0,…,ST-1,AT-1,RT-1,ST)
放入交互经验池.最后,引入折扣因子γ对长远的收益进行折现.
不失一般性,MDP可简化为M=(S,A,R,P,γ),其中,R为R中某个确定性的收益函数,P为P中某个确定的动力学函数.继而限定收益函数的有界性R∶S×A×S→[0,1],序列特性的有界性γ∈[0,1].为了表述的简洁性,使用st,at,rt,r等同于对应的变量表述St,At,Rt,R.进一步在M上定义策略函数的集合
Π={π|π∶S→A},
其中,确定性的策略表述为π(st),随机性的策略为π(at|st),非平稳的策略为π(at|st,t).
一条轨迹的回报Gt为收益的累积和:
在策略π与动力学P产生的所有可能轨迹下求取期望回报,定义状态价值函数Vπ(s)、动作价值函数Qπ(s,a)如下:
记初始状态分布为μ(s0),从而定义关于期望回报的学习目标:
J(π)=Es~μ(s0)[Vπ(s)]=
Es~μ(s0),a~π[Qπ(s,a)].
(1)
因此,强化学习算法根据期望回报最大化的学习目标,在策略集合Π中搜索最优策略:
3 基础问题设定下的发展脉络
智能体、MDP、环境在不同任务场景下,追求的问题特性与建模的任务设定往往侧重点不同,影响着深度强化学习算法的发展.本节详细叙述问题设定视角下,强化学习方法的理论发展与技术方法的进展.
3.1 问题设定的定义
分别表示智能体空间、任务分布、MDP、策略类型、学习目标、环境交互模式这6大设定对象.
M=(S,A,R,P,γ).
在交互框架M的基础上,根据具体场景选择使用θ参数化的策略类型,如显式建模、随机且平稳的策略函数∶=πθ(·|s).
然后,使用恰当的学习目标表征最优策略的性能,如最大化期望回报

图2 问题设定框架
然而,强化学习问题设定的丰富性主要集中在MDP与策略类型,具体如图3所示.
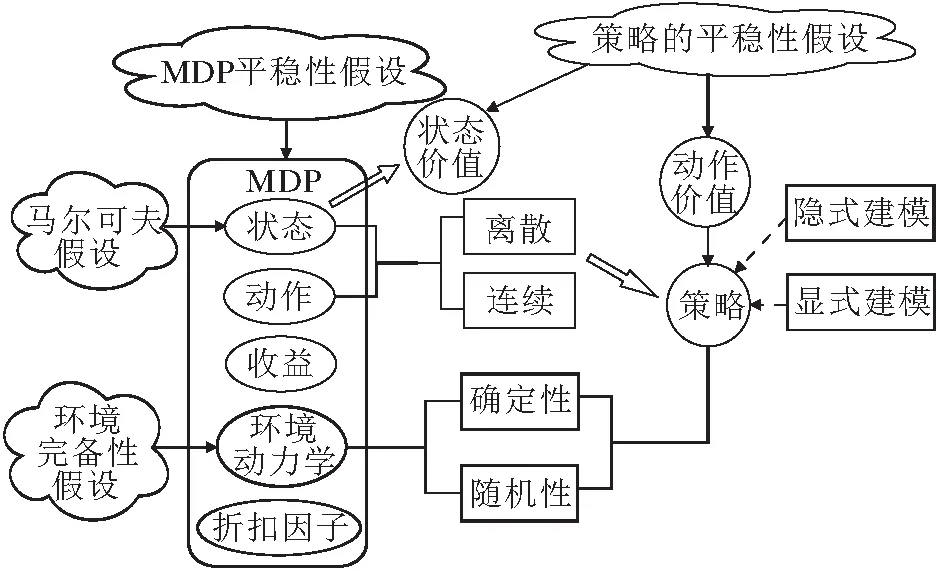
图3 MDP与策略类型的设定
马尔可夫决策过程M=(S,A,R,P,γ)可描述如下.
1)状态是环境系统内部信息的准确表征,智能体决策理应与历史信息相关,即π(at|s0,…,st-1,st),但出于简化序列决策问题的目的,状态空间有马尔可夫性假设,使智能体的决策只依赖于当前状态而与过去无关,即π(at|st).一般而言,状态空间由维度与取值类型这两个角度进行描述,分别为高维或低维、离散或连续或混杂.
2)动作由任务特性所决定,是环境控制量的准确表述,维度和取值类型与状态空间类似.
3)收益函数依据某类“强化物”而设计,是相关任务结果的反馈信号,直接关乎任务在策略集合Π中对应的最优策略子集.
4)环境动力学是环境内部动态过程响应的描述,类型有确定性P(st,at)与随机性P(st+1|st,at).环境动力学默认是未知的,而环境动力学已知的设定被称为环境完备性假设.
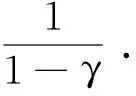
特别地,MDP内的5个元素与序列相关是符合任务场景描述的,如收益函数r(st,at,st+1,t)或环境动力学P(st+1|st,at,t),但与序列相关的特性会增加MDP的复杂度.因此出于简化任务场景的目的,称MDP内的元素与序列特性无关为MDP平稳性假设.故最简MDP定义为M′,主要设定值如下.
1)假设:MDP平稳性假设、马尔可夫假设.
2)状态与动作空间:低维离散,由此构建的MDP也称为表格型MDP(Tabular MDP).
3)收益函数:已知、确定且有界r∈[0,1].
4)环境动力学: 未知,即无环境完备性假设.
5)序列特性: 采用离散时间、无限幕的表述,即T→∞,折扣因子γ∈[0,1),从而确保价值函数的有界性,即
显式建模直接参数化策略a=πθ(·|s),优点在于可根据任务场景设计策略结构,确保策略函数的表达能力.确定策略建模方式后,可选择确定性πθ(s)或随机性πθ(·|s)的策略类型逼近真实的最优策略π*.最后,考虑策略函数与序列特性的关系,称策略与时间无关为策略平稳性假设.因此,显式建模、随机且非平稳的策略类型可形式化表述为
:=πθ(·|s,t).
:
标识最优策略,其策略行为在学习目标的数值上是最优的.然而,期望回报最大化并不一定满足某类行为特性的要求,如鲁棒性、安全性,或契合人类专家的理想行为模式.

表1 交互模式
特别地,表1中的交互模式按智能体与环境的交互成本依次递增.当环境是完备、已知的,智能体与环境的交互成本几乎为零.而均匀交互在设定上引入未知的环境动力学,但“均匀”的交互模式在很大程度上为智能体提供便捷的方式,收集高收益的状态-动作对,更好地评估策略在整个状态动作空间的性能.μ-重置交互打破“均匀”的交互模式,为了搜索最优策略,智能体必须付出额外的交互成本探索整个状态动作空间,确保最终策略的全局最优性.然而,最优策略并不一定会遍历整个状态动作空间,因此专家交互模式为智能体提供引导,在局部状态动作空间内搜索最优策略,有效降低和改善样本复杂度.
值得注意的是,贝尔曼方程作为强化学习的理论基石,有效性主要建立在基础的问题设定上,即单一智能体=1,单一任务=1,最简MDP为M=M′,隐式建模确定且平稳的策略类型
:
期望回报最大化的学习目标
:

表2 基础设定的形式化定义
3.2 基础设定下的理论进展
强化学习最终目的是获取一个策略函数,该策略是否被显式参数化建模,是深入探讨基础设定下理论与技术发展的分类依据.
3.2.1隐式策略建模的理论发展
在基础设定中,强化学习问题可使用经典动态规划算法,如价值迭代(Value Iteration)[1],求得关于策略价值的精确解.具体而言,在离散状态动作空间下,利用贝尔曼最优算子B对表格型Q函数进行迭代,即
Q(n+1)←BQ(n),
经过一定步数后,可得最优Q函数,即
Q(n)→Q*,n→∞.
该设定的特点为,已知环境动力学且在整个状态动作空间更新Q值函数.除了价值迭代,还有基于Q值的策略迭代算法(Policy Iteration)[2],利用贝尔曼一致性算子T对当前策略πk进行策略评估,即
Q(n+1)←TQ(n),
得到Qπk,然后从Q值函数中进行策略改进,即
πk+1←arg maxQπk.
尽管该设定下的经典算法并未体现强化学习的“交互”特性,但为后续理论提供基础的分析思路,如收敛速度、计算复杂度等性能分析.
O(|S||A|ln|S||A|).
这决定相关算法在该设定下样本复杂度的理论上限.
变更基础设定中的交互模式为μ-重置交互:=I3,即环境只支持重置回初始状态分布上,称为基础重置交互.相比均匀交互,该设定下的智能体需要制定探索策略,付出额外的努力去获取新的状态-动作对样本,以保证有足够的样本量覆盖整个状态动作空间.例如,探索策略为UCB(Upper Confidence Bound)的价值迭代算法UCB-VI[32],通过维持历史交互经验中关于状态-动作对的统计量,对新颖的状态-动作施加额外的奖励(Bonus),鼓励智能体的探索朝向潜在的高收益状态.在根本上不同的交互设定决定样本复杂度的下界.
上述理论发展仅与问题设定中交互模式变更有关.进一步地,在基础均匀交互设定下,将最简MDP中的离散状态空间扩展到连续状态空间,于是表格型的表示便不足以精确表达Q值函数.因此,需要寻求Q值函数的近似表示,这从根本上引入函数的近似误差(Approximation Error).为了分析该误差,需要施加线性贝尔曼完备假设(Linear Bellman Completion).首先假定关于Q值的函数集合为
可由专家设计的d维特征φ(s,a)∈Rd和参数向量θ∈Rd进行线性表示:
Q(s,a):=θTφ(s,a),Q∈F.
其次是可行性假设(Realizability Assumption),假设关于任务真实的最优Q值函数存在该函数集合中,即Q*∈F.然后,确保函数在贝尔曼最优算子B迭代后,仍处于函数集合内,即BQ∈F.然而,最优算子的迭代过程
由此,相关理论分析可设计尽可能满足这些假设的强化学习算法,如非平稳策略的LSVI(Least Square Value Iteration)[33].
进一步地,可将线性表示扩展到非线性表示,如神经网络,以涵盖表达能力更强的Q值函数.类似地,理论分析需要最优Q值函数在非线性表示中的可行性假设、在贝尔曼最优算子迭代中的完备性假设及采样数据的分布假设.由此设计的算法,如FQI(FittedQ-iteration)[34],可视为分析深度强化学习算法DQN的理论基础.因此,状态动作空间从离散到连续的设定扩展要求函数的近似表示.这必须施加函数表示的可行性假设、算子迭代的完备性假设等,才能从理论上使误差可控,提供该问题设定下关于样本复杂度的理论分析,为算法的有效性提供坚实基础.
为符合现实任务场景的问题设定,将基础重置交互中的最简MDP变更为连续的状态空间.此时,既要考虑Q值函数的近似误差,又要权衡策略在高维连续状态空间上的探索进度.为此,不仅样本复杂度的上下界应尽量避免与状态空间的规模相关,而且还要对环境的动力学P(s′|s,a)进行相关结构假设,以便更好量化策略的探索进度.于是,该问题设定下理论探讨增添一个额外的核心问题——如何施加最小程度的环境结构假设,找到低样本复杂度的最优策略.
目前的理论研究主要依赖于Bellman Rank[35]和Eluder Dimension[36]这两种对结构复杂度的测量工具.当它们较低时,理论保证能以高样本效率搜索到邻近的最优策略.因此,以相关理论为基础结合深度模型的设计,尽可能满足相关的假设,有利于保障相关算法的有效性.
3.2.2显式策略建模的理论发展
直接建模策略函数能根据问题特性设计策略结构,增强策略的表达能力,其与基础设定的主要不同在于μ-重置交互模式.
类似地,策略函数在离散状态动作空间下为表格型.当扩展到连续的状态动作空间后,策略函数有线性表示或非线性表示.例如,显式建模一个随机且平稳的策略函数,可采用神经网络fθ(s,a)作为非线性表示,Softmax为满足随机且平稳的策略结构:
然而,该问题设定下相关算法分析与隐式策略建模截然不同,需要分析策略的收敛特性[37]而不是策略的价值函数.
策略函数的优化目标(式(1))是非凸的,在理论分析其收敛性时,需要界定优化方法中关于策略梯度的步长,并且对不同形式的梯度施加相关假设,如平滑性假设、近似假设等,以保证策略在优化算法下能收敛于全局最优点.
基于表格型策略、Softmax策略结构及一定条件,策略梯度算法的收敛点正好对应于全局最优策略,但收敛速度却与状态空间的规模呈指数级衰减.为此,相关研究从策略目标上施加正则化项,如信息熵(Entropy)、对数屏障(Log Barrier)等[38],缓解收敛速度较慢的问题.
进一步地,除了参数空间上的梯度优化,还可在策略空间上进行优化,如自然梯度算法NPG(Na-tural Policy Gradient)[39].关于问题设定中的策略类型,不仅局限于表格型,还可延伸到线性、甚至于非线性表示,如Q-NPG[40].或寻找更稳健的梯度优化方式,如信赖域约束下的策略梯度算法TRPO(Trust Region Policy Optimization)[41].
在估计目标梯度中,可借鉴基于动态规划的值估计方法,从而延伸执行者-评估者的算法框架(Actor-Critic, AC)[42],视为广义策略迭代(Genera-lized Policy Iteration, GPI)[1]的特殊形式.这是显式策略建模下最重要的理论成果.具体而言,GPI主要分为策略评估与策略改进.策略评估对当前策略进行价值评估,返回价值函数,是一个关于策略性能好坏的预测问题.而策略改进利用预测的价值函数,以某种方式改进策略,是一个关于如何让当前策略往更大期望回报的方向进行更新的控制问题.在一定条件下,经过不断循环策略评估、策略改进过程,GPI确保策略、价值函数分别能逐渐收敛到最优策略与最优价值函数.由此,GPI提供统一的理论视角以看待强化学习算法.例如:基于价值的策略迭代算法可看作策略评估环节为贝尔曼一致算子,策略改进环节为贪心方式;对于基于策略梯度的强化学习算法,策略评估环节为梯度的近似估计 (Gradient Estimation),策略改进环节为随机梯度优化方法.
3.3 问题设定下技术方法的发展
3.3.1 强化学习交互流程
强化学习方法的基本交互流程如图4所示.首先,智能体与MDP交互,MDP的设定决定智能体内的价值网络与策略网络.其次,历史信息以轨迹样本的形式
τ=(s0,a0,r0,…,sT-1,aT-1,rT-1,sT)

图4 强化学习的基本交互流程图
或转移样本(Transitions)的形式(s,a,r,s′),存储进交互经验池.随后,智能体利用价值网络与交互经验池中的数据进行策略评估,根据价值目标在优化器下对当前策略的价值进行预测.接着,策略网络利用预测的价值函数进行策略改进,策略目标在优化器下指导最优策略的搜索.最后,价值目标和策略目标是策略评估与策略改进的核心.另外,价值网络与策略网络不同的表示、结构、数据正则化都会影响策略的最终性能.
3.3.2隐式策略建模的技术方法
隐式策略建模下的强化学习方法的侧重点在策略评估环节,是对评估策略的价值函数进行参数化建模,利用交互经验对价值函数进行准确估计,解决关于策略的价值函数的预测问题.
价值函数是关于长期回报的期望,对期望估计最直接的方法为蒙特卡洛采样方法(Monte-Carlo Methods, MC).从初始状态分布μ出发,根据当前策略π与环境交互,直到达到终止状态,得到粒度为轨迹形式的交互样本.具体而言,计算轨迹长期回报Gt,以
Q(st,at)←Q(st,at)+α(Gt-Q(st,at))
的方式近似价值函数Qπ(s,a).根据大数定律,在足够多的轨迹样本下,MC能渐进收敛于真实的价值函数.该方法的优点是,在期望意义下无偏差,有利于估计状态子空间的价值.相反地,缺点为方差较大、难以收敛,当状态空间庞大时,要求大量的轨迹样本,而且理论的收敛性要求在均匀交互模式的问题设定下,才能评估整个状态空间的价值.
为了应对μ-重置交互模式的特点——权衡策略的探索进度,以及缓解MC高方差的问题,研究者开始研究时序差分(TD).最早被称为TD(0)的时序差分估计法[1]通过自举(Bootstrapping)价值函数估计当前的价值,避免以轨迹为粒度的交互样本,可用转移样本(st,at,rt,st+1,at+1)对价值函数进行更新,如
Q(st,at)←
Q(st,at)+α(rt+γQ(st+1,at+1)-Q(st,at)).
但是,自举在价值预测时引入偏差.自举的估计方式在最简MDP的问题设定、广义线性表示价值函数的条件下,有严格渐近收敛于真实值的理论保证.
出于探索目的,根据价值估计使用的交互样本,将策略区分成同轨策略(On-Policy)与异轨策略(Off-Policy).具体而言,同轨策略指策略评估过程中的轨迹样本仅来自当前的待评估策略,而异轨策略指用于评估当前策略的轨迹样本可能来自其它策略的交互过程.值得注意的是,异轨的值估计方法与基本理论框架GPI在策略评估环节有微小差异.因此,为了纠正使用异轨策略交互数据估计当前策略梯度而引起的偏差,Glynn等[43]提出重要性采样(Impor-tance Sampling)纠正异轨交互数据的方法.总之,TD虽然克服MC高方差的特点,却在策略评估中引入偏差,而偏差会因策略改进环节的利用而不断累积,在某些场景下的累积偏差会导致非常差的策略性能.
为了更好地平衡价值函数中的偏差与方差,后续研究发展出融合MC与TD的n步自举法(n-step Bootstrapping),并结合资格迹(Eligibility Trace)形成统一的价值估计框架TD(λ)[1].具体来说,其将交互样本粒度为一个完整轨迹的MC和单个时刻的TD,融入n个时刻.特别地,n步自举法可结合用于缓解偏差的双Q学习,或用于纠正偏差的重要性采样和树回溯等方法.虽然增加一定的计算量,但可用资格迹进行内存与计算量的优化.2018年,由De Asis等[44]推广上述MC、TD、n步自举、回溯等方法,提出一个统一的价值估计方法Q(σ).
上述的MC、TD、n步自举方法大多在表格型MDP的问题设定下,有严格的理论收敛性保证,但在应用深度神经网络作为非线性表示以近似复杂场景的MDP时,并无严谨的理论证明,但仍能通过基础的理论分析,设计与解决使用深度网络进行价值近似中遇到的问题.
最初,Mnih等[16]提出利用卷积神经网络建模Q值的DQN,随后在DQN基础上使用双Q学习技巧以稳定训练过程,提出Double DQN[45].Hausknecht等[46]使用循环神经网络满足问题设定中关于状态的一阶马尔可夫假设,提出DRQN(Deep RecurrentQ-learning Network).Igl等[47]从关于环境动力学模型的生成式角度,提出DVRL(Deep Variational RL).
从价值网络结构出发,Wang等[48]选择建模优势函数以降低价值估计的方差,提出Dueling DQN.Bellmare等[49]与Dabney等[50]选择建模期望回报的价值分布,即Q值分布,分别提出C51(Categorical DQN)和QR-DQN(Quantile Regression DQN).特别地,Zahavy等[51]额外构建低价值动作的过滤网络,过滤不理想的动作,提出AE-DQN(Action Elimina-tion).
从探索特性出发,Osband等[52]基于Q值函数的不确定性角度,提出Bootstrapped DQN,指导智能体探索.Fortunato等[53]通过扰动网络层参数的方式,提出适应深度网络探索方法的Noisy DQN.Hessel等[54]结合优先经验池回放PER(Prioritized Experience Replay)、n步自举值估计、建模价值分布等众多技巧,提出Rainbow DQN,深入分析这些网络训练技巧的作用.
在理论上,DQN存在对价值的预测具有过高估计偏差(Overestimation Bias)的问题.Lee等[56]从偏差的角度,通过为目标Q值增加纠正项,缓解该问题.特别地,van Hasselt等[57]进一步分析函数近似表示、自举、异轨策略学习这致命三元素(Deadly Triad)对价值估计的影响.Fujimoto等[58]通过对双Q网络进行裁剪,提出Clipped DQN,缓解高偏差.但是,裁剪却又带来过低估计的问题,Jiang等[59]提出AC-CDQ(Action Candidate Based Clipped DoubleQ-learning),在更复杂的问题设定上,缓解价值过低估计的问题.
近来,Kuznetsov等[60]结合建模价值分布的网络结构、多个价值网络与裁剪的技巧,提出TQC(Truncated Quantile Critic),缓解过高估计偏差的问题.Chen等[20]通过随机选择Q函数子集,计算目标Q值,提出可媲美基于动力学模型的值估计方法REDQ.Peer等[61]进一步分析集成Q函数估计的偏差来源.Li等[62]通过额外构建一个关于参数的后验分布模型,采样Q值函数,提出HyperDQN,相比DQN,提升数倍的样本效率.由此可见,准确性、权衡偏差与方差及利用Q值函数的不确定性可用于指导价值函数的学习过程.
总之,隐式策略建模下的强化学习方法发展脉络如图5所示.

图5 隐式策略建模下的强化学习方法
3.3.3显式策略建模的技术方法
显式策略建模下的强化学习方法的侧重点在策略改进环节,一般对策略函数进行参数化显式建模,融入专家对具体问题的先验知识,构建策略函数的结构表示.从历史交互经验中对当前策略函数进行直接评估,或是借助价值函数进行间接评估,进而解决关于策略函数的控制问题.
早期,Marbach等[63]提出策略梯度定理,直接评估当前策略,直接计算策略目标的参数梯度,为后续的策略梯度算法提供严谨的理论基础.特别地,1992年,Williams等[26]提出REINFORCE,是该理论的一个算法实例.具体而言,直接以蒙特卡洛采样的方式评估策略性能,具有高方差的特点.
相比直接计算策略目标的参数梯度,2001年,Kakade等[39]提出NPG,利用费舍尔(Fisher)信息矩阵将参数梯度投射到策略梯度,让原本在参数空间的策略搜索变为策略空间中搜索,使梯度的信息与策略目标的关系更紧密.进一步地,2017年,Liu等[64]提出在核函数空间进行策略搜索的SVPG(Stein Variational Policy Gradient),缓解维度灾难的问题.此外,Wu等[65]使用K-FAC(Kronecker-Fac-tored Approximation Curvature)的优化方法计算策略梯度,使梯度信息带有二阶信息,此方法称为ACKTR(Actor Critic Using Kronecker-Factored Trust Region).
除了直接计算策略梯度以评估策略性能外,还有借助特定评估量间接评估的方式.特别地,该评估量可为参数化的价值函数,以此近似计算策略目标的梯度,达到策略改进的目的,也称为AC框架.然而,近似计算的方式会引入相应的误差.
从方差的角度分析误差来源,使用同轨数据对价值函数的估计方式是无偏的,但却需要大量的样本数据,否则策略性能会面临高方差的影响.为了权衡数据量与高方差的影响,Mnih等[66]从分布式架构的角度出发,提出使用同轨策略在线进行多样性数据收集的A3C(Asynchronous Advantage Actor-Critic),稳定提高数据质量,降低方差.在此基础上,进一步使用同步(Synchronous)协调器的A2C(Advantage Actor-Critic)能更有效利用GPU资源.Espeholt等[67]在交互经验池中引入重要性采样,改善上述分布式架构,于2018年提出IMPALA(Im-portance Weighted Actor-Learner Architectures)架构,改善样本复杂度.特别地,Horgan等[68]提出分布式架构Ape-X,采用回放机制对交互经验池中的重要数据进行优先采样,提高样本的利用效率.
不同于提高数据质量的思路,Schulman等[41]观察到策略参数的微小变动会显著影响策略行为的表达,引起同轨策略的不稳定性问题,于是借鉴“裁剪”技巧可降低方差的思想,提出TRPO,以信赖域的约束方式限制策略更新过程中的剧烈变化.然而TRPO中关于费舍尔信息矩阵的计算开销过大.2017年,Schulman等[69]提出PPO(Proximal Policy Optimization),以近似计算的方式简化TRPO中关于费舍尔信息矩阵的计算,成为当下广泛应用的同轨策略算法.然而,同轨策略对数据量的要求处于百万级别,难以走进现实的应用场景.
从偏差的角度分析误差来源,使用异轨策略的交互数据对价值函数的估计是有偏的,但能充分利用历史数据降低方差,提高样本效率,使样本量迈入十万级别.具体而言,Degris等[42]提出基于异轨的AC框架——Off-PAC(Off-Policy Actor-Critic),从偏差角度进行理论分析.Wang等[70]提出ACER(Actor-Critic Experience Replay),从交互经验池的角度扩充A3C的分布式架构,并结合异轨策略的数据以降低方差.进一步地,当策略类型为确定性时,Silver等[71]提出确定性的策略梯度算法DPG(De-terministic Policy Gradient).若动作从离散扩充到连续,Lillicrap等[72]提出针对连续动作的算法DDPG(Deep DPG).为了改善DDPG的不稳定性问题,Fujimoto等[58]提出构建两个动作价值函数进行策略改进的TD3(Twined Delayed DDPG).针对随机性的策略,Abdolmaleki等[38]结合同轨策略与异轨策略的优势,提出可同时作用于离散动作和连续动作的MPO(Maximum a Posteriori Policy Optimiza-tion).Haarnoja等[27]提出基于最大熵框架的SAC,从探索的角度缓解价值估计的偏差.特别地,Duan等[73]借鉴QR-DQN对价值分布的建模,提出在SAC基础上建模价值分布以进行值估计的DSAC(Dis-tribution SAC).
近年来,Agarwal等[74]对策略的探索进度进行量化,提出PC-PG(Policy Cover-Policy Gradient).Cobbe等[75]提出PPG(Phasic Policy Gradient),在PPO的基础上引入辅助训练阶段,显著提高样本效率.Liu等[76]提出OPPOSD(Off-Policy Policy Opti- mization with State Distribution Correction),针对异轨策略的偏差来源,在ACER的基础上纠正行为策略与目标策略之间的状态分布偏差.特别地,在SAC的基础上,Lyu等[77]建模两个策略网络以辅助探索,进一步探讨价值纠正(Value Correction)和策略正则项(Policy Regularization)对算法性能的影响,从而提出DARC(Double Actors Regularized Critics),相比SAC而言,提升近70%的策略性能.
总之,显式策略建模下的强化学习方法发展脉络如图6所示.
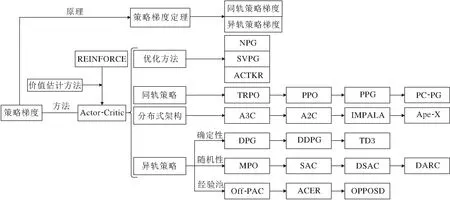
图6 显式策略建模下的强化学习方法
3.3.4强化学习评估环境
本节简要介绍如下深度强化学习方法的相关评估环境:Atari[78]、MuJoCo(Multi-joint Dynamics with Contact)[79]、DeepMind Lab[80]、Stochastic Deep Sea[81]、PySC2[82]、CARLA[83].
具体介绍如表3所示.

表3 常用的评估环境特点
基于价值的方法一般适用于离散的动作空间,如DQN用在以图像为输入形式的Atari游戏.特别地,连续型矩阵用于强调状态为图像.
针对连续的动作空间,常用的环境为MuJoCo.较特殊的Stochastic Deep Sea主要用于评估算法的探索效率.复杂的场景常有混杂的状态动作空间,即图像类的连续型矩阵、传感器类的连续型向量、目标类的离散型向量等混杂空间类型,如自动驾驶的仿真平台CARLA.
这些常用的评估环境如图7所示.

(a)MuJoCo
常用的同轨策略算法和异轨策略算法在常见的连续控制任务上的基准结果如表4所示.这些任务的共同目标为:让不同关节结构的机器人尽可能快速地往前跑,由此设计相关的收益函数.结果的评估方式为:计算多次独立实验后关于幕的平均总回报与标准差.PyBullet[84]是替代MuJoCo对机器人关节动力学进行仿真的物理引擎,在其上的相关任务更困难.
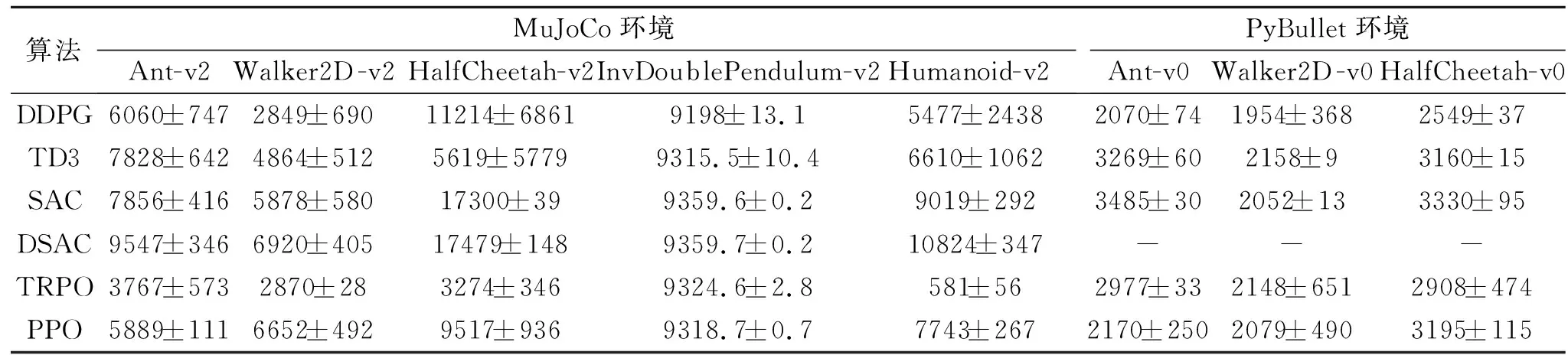
表4 常见的连续动作控制任务的基准结果
值得一提的是,收益函数并不能准确表达理想行为模式,这意味着总回报越高,并不代表策略越优.当收益函数在精确设计的条件下,相关任务的评估指标才能更好地衡量不同算法的优缺点.
同样地,常用算法(A2C,DQN,TRPO,PPO,ACER,ACKTR)在Atari[78]环境中以图像为输入、离散动作为输出的常见任务上的基准结果如表5所示.

表5 Atari环境下离散动作控制任务的基准结果
此外,关于相关算法的基准结果会受到诸多因素的影响,如算法的超参数、实现方式的差异、任务设置、所需样本量.因此,需要制定统一、合理的策略评估方式,对不同算法的各方面性能进行有效对比,如基础的强化学习算法库Stable-Base-lines3[85]在统一评估标准下提供可供参考基准结果.
4 强化学习问题的延伸设定
本节进一步延伸强化学习其它问题设定,梳理强化学习各子领域的内在逻辑关系及其主要动机,整体结构如图8所示.下文从学习目标、策略类型、MDP、任务、智能体这五个设定对象进行叙述.
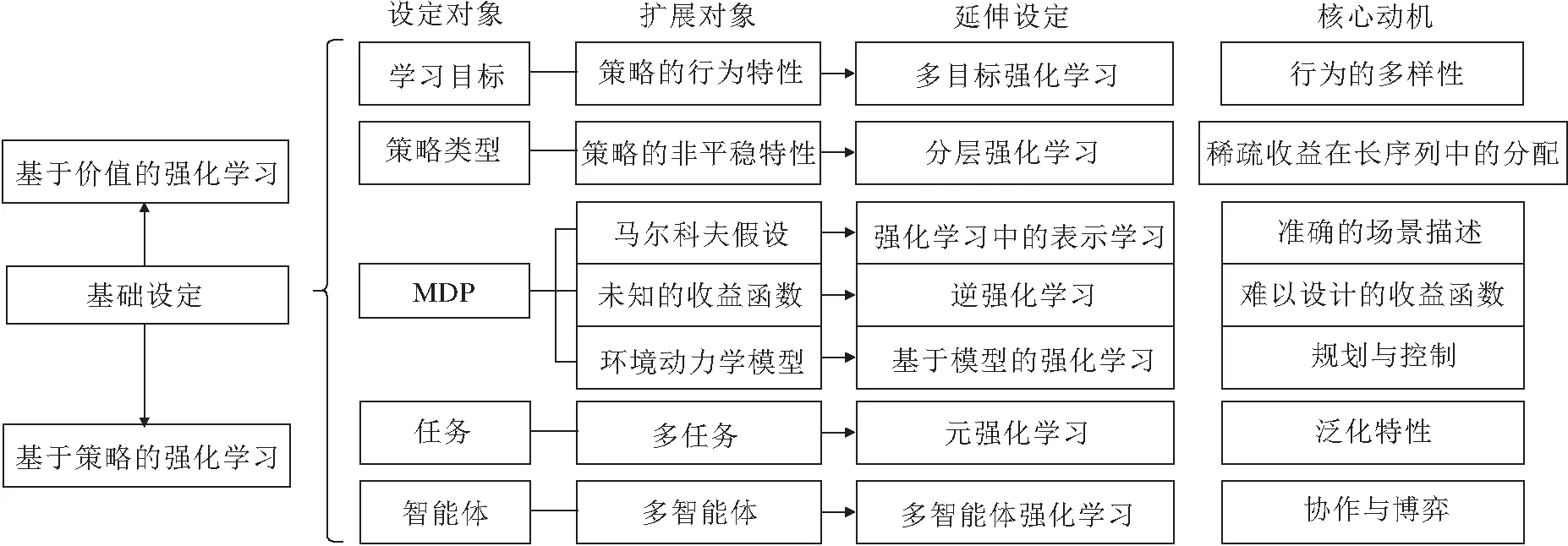
图8 强化学习方法延伸设定的主要逻辑
4.1 多目标设定
从单一学习目标到多目标关于行为特性的扩展,其延伸设定称为多目标强化学习(Multi-ob-jective RL)[86].核心动机为:理想行为模式不仅只满足于完成任务,还需要考虑行为模式的其它特性,如安全性、鲁棒性、收敛性、可解释性等问题特性.由此构建相关辅助目标,设计强化学习算法,使其在策略集合Π中搜索既满足期望回报最大化,又符合某种行为特性的策略.形式化表述如下.
将
M=(S,A,R,P,γ)
中的单个收益函数根据问题特性扩充到多个,该问题设定MDP称为MOMDP,其中
R=(r1,r2,…,rm)T,γ=(γ1,γ2,…,γm)T,
m为目标数量.于是,第i个目标定义如下:
其中μ为初始状态分布.特别地,使用wi作为第i个目标的权重系数,满足
于是关于多目标的策略学习目标为:
多目标强化学习的难点在于,如何搜索到合适的策略,以平衡多个目标,因为目标之间往往是相互冲突的.如导航小车以到达目的地为任务,主目标为到达目的地,而辅助目标希望既要速度快,又要能耗低,但速度与能耗这两个辅助目标是冲突的.因而,多目标强化学习可借鉴与策略约束有关的研究思路,通过将问题特性设计为待优化的辅助目标,来学习复杂行为.
4.2 策略类型的设定延伸
不论隐式建模还是显式建模,针对随机性或确定性的策略类型,在基础设定中均有一定程度的探讨,如DPG[71]、SAC[27],但是它们都基于策略平稳性假设.
因此,策略从平稳性假设扩充到非平稳性,其延伸设定称为分层强化学习(Hierarchical RL, HRL)[12],是关于策略在序列特性的扩展.核心动机为:当涉及到一个长序列的复杂场景时,序列特性为平稳的策略π(at|st)不足以描述复杂行为,面对稀疏的收益信号,难以有效进行效用分配.因此,需要考虑对序列特性进行分层,拆解长序列与复杂行为,采用分而治之的解决思路.而时间序列是序列特性的直观形式,于是从最微观层面可认为每个时刻t均对应一个策略π(at|st,t).直观地,π(at|st)是全局策略的形式化表述,π(at|st,t)是局部策略的形式化表述,自然的分层策略可表述为π(at|st,gt),其中gt为时刻的抽象表示(Temporal Abstra-ction),是对复杂行为意图的分解,如
gt=f(st,t),
基本结构如图9所示.
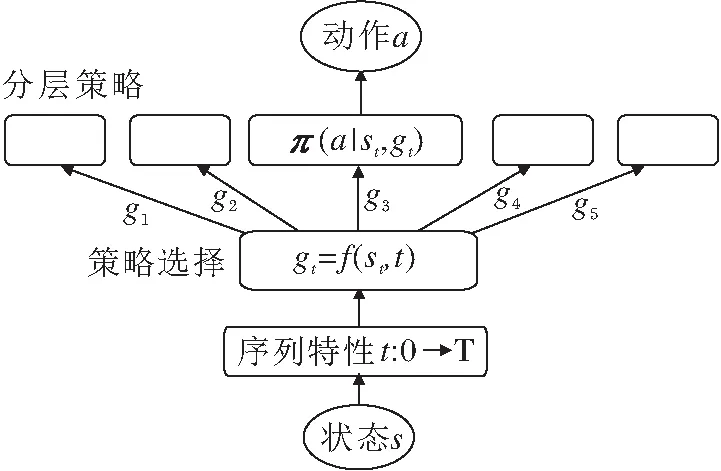
图9 HRL基本结构
例如,在机械臂拿起锤子敲钉子的任务中,主目标是敲钉子的收益r1,辅助目标为拿起锤子的收益r2.那么,由基础设定下的强化学习算法训练得到的策略行为,往往只会拿起锤子或仅用机械臂敲钉子.原因是拿锤子、敲钉子该理想行为在序列特性上存在先后的顺序关系,与时刻相关,但在基础设定下被策略平稳性假设所简化.
分层强化学习的难点在于:如何自动化地抽象层级关系,即哪些时刻对应子行为模式;如何学习这些子行为模式对应的分层策略;如何组合这些分层策略为理想的行为模式.
特别地,针对稀疏收益、长序列的具体场景而言,应用分层强化学习,人为设计层级关系是强化学习在落地过程中十分有效的手段[87].尽管这意味着相关方法在一定程度上损失泛化性能.进一步地,非平稳性的设定可同样扩展到收益函数、环境模型、价值函数等对象.
4.3 MDP的设定延伸
4.3.1 收益函数
从已知的收益函数扩展到未知的收益函数,其延伸设定称为逆强化学习(Inverse RL)[88].核心动机为:在复杂场景下人为根据任务特性设计准确的收益信号是较困难的.精准地把握任务特性, 需要对领域知识具有深入了解.
于是,可通过理想行为模式的数据,如专家示教数据,以数据驱动的方式学习收益函数的表示,并求解最优策略,形式化表述如下.
理想行为模式的数据以轨迹形式表述为
τ*=(s*0,a*0,s*1,a*1,…,s*T),
参数化建模的收益函数表述为rη(s,a).如图10,构建理想行为模式的轨迹分布pη(τ),引入一个二值的最优变量Ot,令

图10 理想行为模式的概率图
p(Ot=1|st,at)
表示当前时刻的状态和动作值是最优的概率.
具体而言,选择
p(Ot=1|st,at)=exp(rη(st,at)),
于是有
特别地,若同时参数化策略πθ,其轨迹分布为πθ(τ),通过JS散度拉近两分布的距离,得到如下逆强化学习的优化目标:
该优化目标是要寻找参数η,来获得理想行为的轨迹分布与当前策略的轨迹分布差距较大的收益函数.再在当前收益函数rη(s,a)下寻找最优策略πθ,两者相互迭代优化,找到关于任务的最优策略π*与收益函数表示r*.
逆强化学习方法的难点是,如何在训练得到的收益函数表示下求解最优策略.主要原因有:1)关于理想行为的数据集存在噪声且可能对应多个收益函数,拟合结果并不确保收益函数唯一;2)强化学习方法对收益信号的数值、表示十分敏感,在可能存在多个收益表示时,求解策略往往差强人意,出现非常差的策略性能.
尽管逆强化学习能直接从理想行为数据集上获取相关策略,但是其额外增加对数据集数量与质量的要求与拟合收益函数的计算开销.针对难以设计收益、数据集易于获取的问题场景下,结合逆强化学习与模仿学习(Imitation Learning),能进一步达到更稳定的性能.
4.3.2环境动力学模型
从未知的环境动力学到环境动力学模型的扩展,其延伸设定称为基于模型的强化学习(Model-Based RL)[9].核心动机为:追求一个高样本效率的最优策略,智能体不应只从交互式的试错经验中学习,还能通过交互经验构建环境动力学模型,预测环境的动态特性,从而让智能体具备规划与控制的能力.追求的问题特性为效率性,对模型结构的选择、学习与利用具有较高要求.
从交互经验或相关数据中构建关于环境动力学的数据集
参数化环境动力学模型Pψ(st+1|st,at),通过最大似然目标
进行学习.这是一个典型的监督学习问题,关于Pψ的建模方式自然会因具体任务场景、函数表示、优化算法的不同而有丰富多样的方法.
因此,相关强化学习方法可结合环境动力学模型进行规划、控制,如同时参数化策略πθ.在已知模型Pψ下求解策略,根据策略的交互经验继续训练动力学模型,目标可表述为
基于模型的强化学习的难点在于如何处理环境模型的不确定性与近似误差(Approximation Error).当环境动力学过程过于复杂时,模型的误差会在不断的策略利用中积累,在长序列决策问题上造成不理想的结果.
在决策或规划过程中,当出现数据集未曾出现或频率极少的状态动作时,模型的不确定性会造成严重的策略偏差.
尽管,基于模型的强化学习能利用环境模型对样本复杂度、探索效率、安全性、适应性、可解释性等强化学习中的挑战进行显著改善,但却引入额外的计算开销和因不确定性与近似误差带来不稳定性问题.针对交互样本获取成本昂贵、有深厚领域知识支撑的问题场景,基于模型的强化学习能显著改善样本复杂度,并对非平稳环境提供自适应的模型支持[89].
4.3.3马尔可夫假设
拓宽基础设定中的马尔可夫假设,可视为MDP中对状态定义的扩展.核心动机认为:马尔可夫假设限制关于问题场景的准确描述,使智能体每个时刻的决策并未考虑历史信息,造成策略性能无法继续提升.决策信息的缺乏从根本上成为限制性能的瓶颈,从而需要提取关于状态的抽象表示(State Abstraction).
具体而言,许多问题场景是难以获取其内部信息准确表征的,即环境并非完全可观测,不能简单地将状态等同于环境观测,需要从中抽象观测空间,该延伸设定称为POMDP(Partially Observable MDP)[90].形式化描述如下.
将M=(S,A,R,P,γ)扩展成(Ω,O,S,A,R,P,γ),其中,Ω为观测空间,O∶S×A→Ω为观测函数,表示对于O(a,s′,o)任一动作与其到达的下一状态下、产生观测值为o的概率.通过相关编码器f对历史观测信息进行抽象,如
st=f(o0,o1,…,ot-1,t),
得到状态的抽象表示.
状态表示的学习难点在于如何从历史信息、序列特性中准确提炼对决策有帮助的表征.具体地,状态表示与具体问题场景强相关,状态编码的准确性是策略决策的基石,从根本上决定任务的可行性.
针对具体的问题场景,尽可能采用人为定义状态以准确表征环境的内部信息.当面对高维复杂的场景,如图像、传感器等混杂状态空间时,需要寻求该设定下的状态表示方法.
4.4 多任务设定
将基础设定中的单一任务扩展到多任务,是关于任务数量对学习机制的扩展,其延伸设定称为元强化学习(Meta RL)[13].在这个扩展中,核心动机认为:要追求一个泛化性强的最优策略,智能体不应只从单一任务的交互经验中学习,而是在多任务下提炼共同的元策略,从而面对新任务时也能快速泛化.因此,元强化学习的着重点在于任务级的泛化性.形式化表述如下.
假设有n个训练任务集的MDP:
Mtrain={M1,M2,…,Mn},Mi=(Si,Ai,Ri,Pi,γi),
测试任务集为Mtest.在基础设定下,第i个任务的最优策略参数为:
可简记为
θ*=fRL(Mi).

接着,寻找元模型的最优参数φ*的方式为
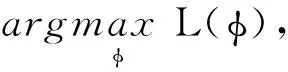
其中L为策略学习目标.
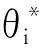
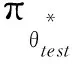
特别地,当元模型f和策略学习目标L均采用策略梯度作为优化方法时,具体方法称为MAML(Model-Agnostic Meta Learning)[91],是元强化学习算法中极具影响力的工作.
元强化学习的难点在于任务分布的设置及元模型结构的选取.任务分布决定泛化性能的方向,如迷宫环境中不同类型的迷宫不会设置为差异太大的任务.其次,元模型结构的选取多种多样,每种结构均有优缺点,在不同场景下表现各不相同.
此外,针对具体问题场景元强化学习提供任务级的泛化特性,代价是需要精心设计相关的任务分布,以及因寻找适应问题场景的元模型结构而付出的计算开销.
在多任务的问题设定下,元强化学习的对象不仅为策略,还可为环境动力学模型、网络结构、MDP等对象[89].元强化学习逐渐成为强化学习研究中热门的子领域,是探讨强化学习算法泛化性能的切入点.
4.5 多智能体设定
将基础设定中的单一智能体扩展到多智能体,是关于智能体个数对学习机制的扩展,延伸设定称为多智能体强化学习(Multi-agent RL)[92].核心动机为:为了描述真实场景下协作与竞争关系,智能体不仅是自身与环境交互的简单关系,还有跟其它智能体的合作与博弈等复杂关系.因此,在早期便有针对多智能体在复杂任务场景下学习机制的相关研究.一般而言,多智能体完成任务的3种方式为协作、博弈或两者兼之,由此设计各智能体对应的MDP.
多智能体强化学习的难点在于多个学习目标、MDP的非平稳特性和多样化的信息结构.具体而言:1)对于每个智能体而言,学习目标一般是多样的,既需权衡竞争者策略,又要考虑合作者的状态,还要满足自身收益.2)MDP的非平稳性指单个智能体面对的环境动力学是非稳态的,因为环境是根据多个智能体的共同作用而返回下一状态的,但对于单智能体,它不一定能看见所有其它智能体.这导致理论分析上的困难.3)多智能体之间的信息结构设计是多样的,如中心化、去中心化或拓扑结构,具体如图11所示.

图11 多智能体的信息结构
总体看来,多智能体是最复杂的问题设定,其还可包含多任务场景下的泛化性、MDP与策略的非平稳性及多目标下的强化学习问题.进一步地,在多智能体的设定下,强化学习与博弈论产生深刻联系,并从中寻求相关的理论基础,如纳什均衡.
5 交互模式的延伸设定
基础设定中已阐述关于环境完备性、均匀交互和μ-重置交互模式的相关内容.本节关注专家交互和离线学习这两种交互模式,重点综述专家交互的相关方法.作为延伸设定的分析示例,在问题设定下梳理子领域的发展逻辑.
5.1 专家交互
专家交互是一种半交互方式,主要有在线的专家反馈和离线的专家数据.从离线专家数据中学习称为示教学习(Learning from Demonstration, LfD)[93].核心动机为:利用专家数据对效用分配、探索与利用进行指导.在基础设定下,价值和策略函数在评估和改进环节迭代到收敛,常常需要百万级别的样本量,阻碍其进一步的发展.于是,自然可以利用专家行为数据蕴含的监督信息来改善高样本复杂度的难题.
专家交互方法的大致流程包括专家数据的获取方式与类型、从专家数据中提取知识表示、知识表示对设定对象的指导方式、指导方式中的反馈机制,具体如图12所示.
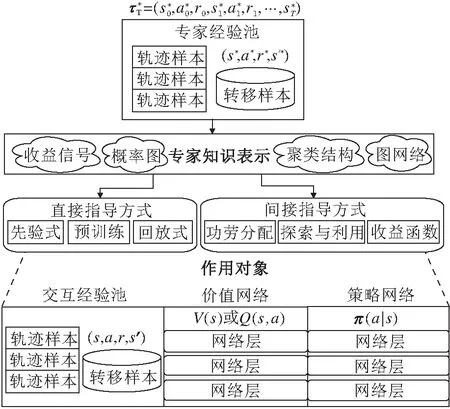
图12 专家交互方法的示意图
5.1.1直接指导方式
本节主要分析先验式(Prior)、预训练(Pre-train)、回放式(Replay)这3种直接指导方式,根据其指导对象与作用机理,分析并讨论直接指导方式的优缺点.
1)先验式.指导的对象为价值网络,主要动机是希望策略评估过程中,动作价值函数能对专家的状态-动作进行合理地效用分配.例如, 将专家经验池直接加入异轨强化学习算法的交互经验池中,然后由价值网络的学习目标对专家经验池进行采样学习.在此基础上,大多数强化学习算法均有先验式版本,如DQfD(DeepQ-learning from Demonstrations)[94].
2)预训练.指导的对象可为策略网络或价值网络,主要动机是给策略在状态动作空间中一个好的初始点,使其更接近专家策略.例如,预训练策略网络πθ(a|s)将专家经验池的数据处理成适合监督学习的形式De={(s*i,a*i)}.由此,进一步最大化对数似然学习目标
称为行为克隆(Behavioral Cloning, BC).然后,把预训练后的策略参数作为智能体中策略网络的初始化参数.同样地,各类异轨强化学习算法均使用预训练技巧,如SAC+BC[93].
3)回放式.指导对象为交互经验池,主要动机是修改交互经验池的采样机制,不应用随机采样,而是采用某种回放机制对专家数据进行优先采样.例如,优先经验池回放PER[54],基于当前动作价值函数,为每个转移样本(Transition)计算时序差分误差(TD-Error).根据误差项设定优先度系数,优先度系数越高,被采样的概率也越高.因而,专家数据样本往往被设置为较高的优先度系数.
下面说明直接指导方式的性能与缺点.
1)先验式的指导方式在Actor-Critic框架下效果十分有限,因为价值网络的学习目标是评估收集交互经验池中所有经验的行为策略,而不是目标策略网络.由贝尔曼一致性方程可知,行为策略与当前策略之间存在策略分布上的偏差,使直接加进交互经验池中的专家示教数据并未起到理想的作用,反而起到影响策略评估过程的负作用.实验表明,单一的先验技巧在大多数异轨强化学习算法中的性能改进并不显著[95].
2)预训练的指导方式在大多数场景下能轻微提高策略性能,原因是专家示教数据是通过最大对数似然的学习目标将“专家知识”以预训练的方式传递给策略网络.因此,只要策略参数能得到一个好的初始点,就能避免陷入前期探索过程的低效.但是,如何充分利用专家示教数据获取一个好的起点,是一个极具工程性与技巧性的问题,需要对数据进行大量的清洗并获取特征,将预训练的技巧用至恰到好处.
3)回放式的指导方式能明显提升策略性能[96].主要原因是:通过强化学习的基础机理,如TD误差或策略分布的偏差,对交互经验池中的样本进行选择性采样,使价值网络评估的行为策略不再是表示整个交互经验池,而是与当前策略发生关联,更符合理论框架GPI中的理论条件,如策略评估的对象为当前策略、策略评估过程需要迭代价值网络到收敛等.尽管如此,“交互”的属性让策略与交互样本之间存在相互影响,难以满足理论分析中对交互经验池样本的质量、分布假设等条件的保证.为此,需要大量的实验评估,才能从统计意义验证回放式指导方式的有效性.
总之,直接的指导方式将专家轨迹数据中的收益信号直接当作专家的知识表示,其特点为关注智能体的外部状态,如初始化状态分布、经验回放方式等.
5.1.2间接指导方式
本节简要介绍作用于价值、策略、收益函数的间接指导方式及方法背后的主要动机.
1)作用于价值网络的学习目标,在策略评估环境利用专家知识表示如收益信号,指导智能体的效用分配问题.主要动机为:以某种具体约束方式在价值目标中突出专家状态-动作对出现的回报,如NAC(Normalized Actor Critic)[97].
2)作用于策略网络的学习目标,在策略改进环境利用专家知识表示隐含的专家策略,对智能体的探索策略进行指导.主要动机为:对策略分布的偏差施加分布约束,让当前策略与专家策略的联合分布满足软约束,建模约束中的专家分布抑或是添加行为克隆的损失函数的TD3+BC[98]等.
3)作用于收益函数的表示学习,共同指导智能体的效用分配、探索与利用.主要动机为:从专家行为数据中捕捉具有参数化结构的收益函数.例如,使用最优变量的概率图模型建模专家行为,通过参数化的收益函数捕捉专家数据中的知识表示[99].
整体看来,间接指导方式不如直接指导方式简洁,需要额外提取专家知识表示,而且理论分析也较为困难,目前尚未建立通用的算法框架.但是,间接指导从离线数据中学习到的知识结构,具备更强的泛化能力,相关研究已建立起了与示教学习算法框架[88]的联系.然而,如何在环境交互中更有效地嵌入专家知识,仍是一个开放性问题[95].
5.2 离线强化学习
扩展问题设定中的离线学习交互模式使智能体在完全离线的数据集上学习,此延伸设定被称为离线强化学习(Offline RL)[10].核心动机为:在一个离线的行为数据集上学习一个与环境交互表现良好的策略.该问题设定更追求实用性,零交互的任务设定使智能体失去交互特性,也让策略失去探索特性.因此,离线数据集的质量决定策略性能的上限.
Agarwal等[100]的研究为离线强化学习的可行性提供积极的研究结果.在数据集足够大,多样性足够丰富的条件下,离线方法REM(Random Ensemble Mixture)在Atari游戏上超过在线交互的DQN.
在探索受限的条件下,离线强化学习面临分布偏差和策略评估这两个核心难点.分布偏差指离线数据集与环境交互之间的状态动作分布偏差;策略评估是当策略无法在环境交互中得到评估时,如何利用离线数据“准确地”评估策略性能.这是离线交互的问题设定特有的局限.针对分布偏差,当前研究从策略约束和值函数估计中的不确定性出发,缓解由离线数据的分布差异引起的偏差来源.对于离线的策略评估,只能借助环境动力学模型的建模近似计算,这也意味着引入模型的近似偏差,极易造成策略评估的不准确性.因此当前这些难点是相关解决方法的主要瓶颈.此外,离线强化学习强调问题设定变更——离线交互,创造借鉴监督学习相关思想方法的可能性,增强强化学习方法的实用性,在不少应用上都具有较优的性能表现.
6 结 束 语
6.1 问题设定驱动的方法论
从问题设定视角上看强化学习,选择如下经典算法:VI[1]、SAC[27]、FQI[34]、DQN[45]、PPO[69]、DDPG[72]、OPPOSD[76]、Option-Critic[87]、 f-MAX[88]、 MBMRI
(Model-Based Meta-RL)[89]、MAML[91]、OERLwD(Over-
coming Exploration RL with Demonstrations)[93]、REM[100]、QMIX[101].相关设定如表6所示.
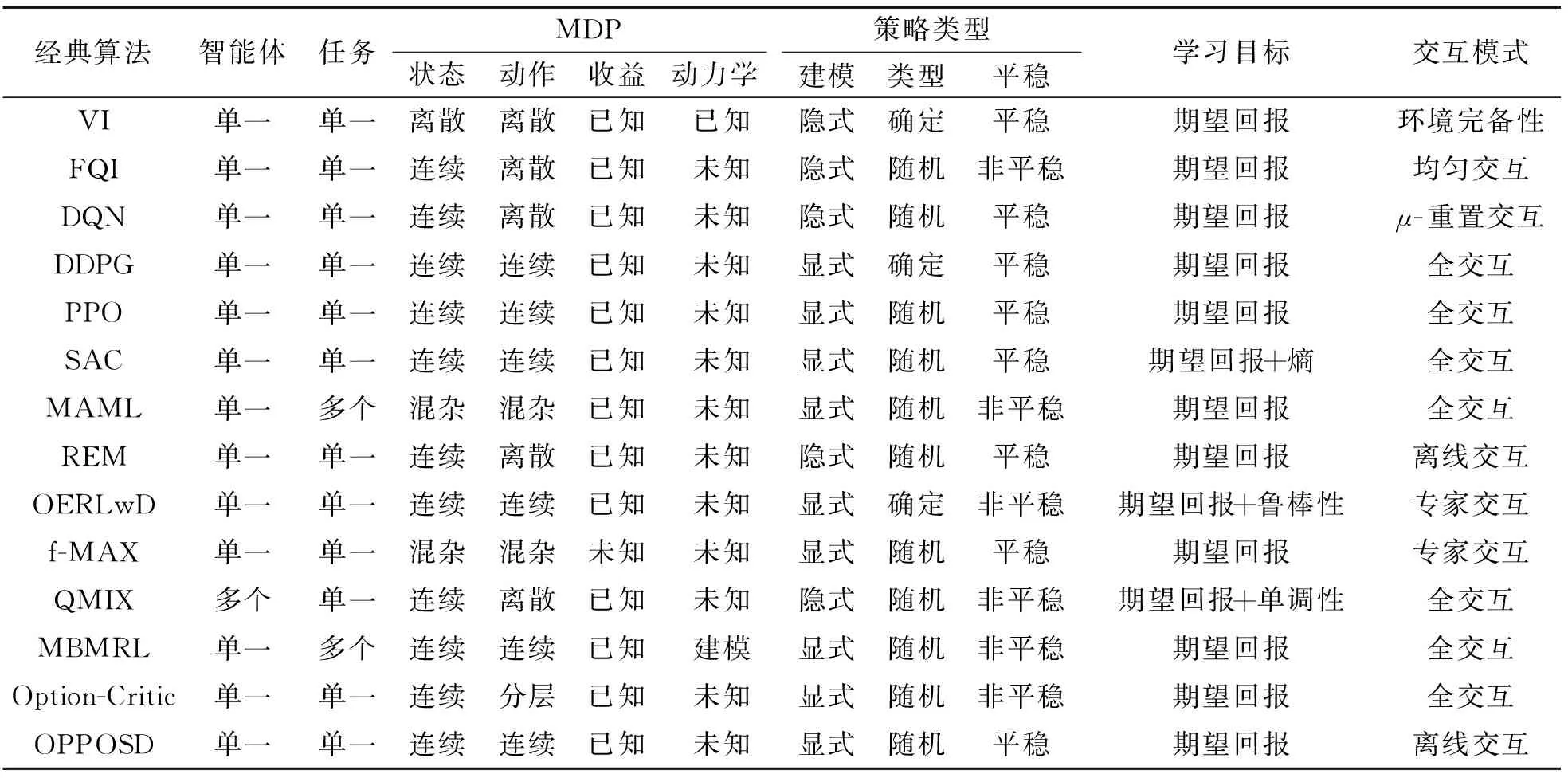
表6 经典算法的问题设定
以具体任务场景为驱动,从问题设定视角看待强化学习各研究方向的技术,可遵循如下方法论:
1)根据任务场景,从智能体、任务、MDP、策略类型、学习目标、交互模式6个设定对象确定场景的具体问题设定,选择策略函数或价值函数的建模方式.
2)在具体问题设定基础上,从经典算法设定中选择合适的解决方案,得到基准结果.
3)在基准结果上根据问题特性融合、借鉴强化学习各研究方向的关键技术.例如:由于任务场景的长序列特点,选择非平稳策略的建模方式,再借鉴分层强化学习的思想方法;若具备任务场景的相关领域知识,为了提高解决方案的样本效率,选择建模未知的动力学模型,采用基于模型的强化学习方法;若追求策略的泛化性能,可在多任务设定下构建任务分布,融合元强化学习的思想方法.
6.2 当前研究热点
经过近年来的发展,基础设定下的强化学习方法的有效性已得到充分验证,基本理论也趋于完备,在众多新领域和应用上也取得突破[4-5,21].然而在走向现实应用场景时,现有方法仍主要面临高样本复杂度与仿真环境的制约.因此,当前研究热点主要集中在如下几方面.
1)基础的两大核心挑战——效用分配和探索与利用对智能体学习效率的影响.效用分配的方式以价值函数为主,早期使用价值函数建模期望回报的方式[45],具有高偏差、鲁棒性差的特点.随着应用场景的复杂化,一个准确、平滑、鲁棒的价值函数是至关重要的.因此,Li等[62]提出HyperDQN,建模价值函数分布以权衡偏差与方差,Chen等[20]提出REDQ,在多样的函数结构中随机化策略的评估值,用于确保准确性的同时提升鲁棒性.对于探索与利用,除了基于信息增益和不确定性的探索方法[30],研究者们更集中于寻找对通用场景都尽可能有效且简单的探索原则,如“返回到高收益状态,再随机探索”[29]以提升探索效率,从而改善高样本复杂度的难题.
2)为了摆脱仿真环境的制约与高昂的交互成本,充分利用离线的大型数据集学习最优策略,研究者们把目光投向离线强化学习.一方面,离线的固有缺陷要求数据集具备丰富的多样性.因此,如何准确定义、表示、量化数据集上的多样性成为了当下的研究热点,如有研究者提出NeoRL(Near Real-World Offline Reinforcement Learning)[102]等数据集与评估准则.另一方面,离线评估容易引起策略学习过程中的分布偏差,有研究者提出OPPOSD[76]等策略约束的方法,来降低偏差的影响.尽管此类方法存在过于保守的缺点,但在特定场景中也有不错的性能.而REM[100]从价值函数的不确定性角度尝试解决分布差异缓解过于保守的缺陷,但实证研究却表现出鲁棒性较差的缺点.此外,为离线强化学习提供更有效的理论保证的相关研究、指导相关的算法设计也成为当下的研究热点.
3)除了通过解决两大核心挑战缓解高样本复杂度的研究思路,还存在通过变更问题设定进一步提高样本效率的研究方向.当研究者具备领域的专业知识时,面向问题设计特定结构与表示的动力学模型,即基于模型的强化学习研究方向[9],在付出额外计算成本与牺牲泛化性能的前提下,能显著地将样本利用率提高一个量级,是强化学习在单一场景下落地的有效方法.若不希望牺牲泛化性能,在策略学习过程中引入专家交互模式的研究思路[93],充分利用专家知识纠正策略偏差且维持技术框架的可扩展性与泛化性[95],是当下热门的研究方向.
6.3 未来发展趋势
尽管强化学习在近年来发展迅速,但在面向现实场景与新问题的应用时,仍面临不少挑战.
1)从问题设定驱动的整体视角上看,强化学习面临架构设计的挑战.在现实场景中,状态动作空间的不同设定、策略建模的不同选择或是超参数的不同扰动都会显著影响强化学习方法的性能表现.目前大多数方法都是通过专家经验式建模或启发式搜索的方式进行架构设计,这无疑给新问题的解决增加复杂性[103].因此,如何针对现实场景自动化设计强化学习解决方案,是一个未来值得研究的课题[104],如面向问题MDP的自动化建模、超参数的自适应优化、深度网络结构的自适应调整[105]等.
2)强化学习方法的有效性在大多数场景下已被验证,但其泛化性仍未被很好地解决.目前改进泛化性能的方法大多基于元学习与迁移学习,从与目标任务相近的任务分布中提取有效的特征以改善目标任务的学习效率,但目前方法任务分布的覆盖面较窄,有效特征的定义也较模糊.因此,借鉴计算机视觉与自然语言处理领域中大模型的预训练思想,训练相似问题设定下的强化学习大模型以帮助智能体高效解决目标任务,是值得研究与探讨的方向[106].此外,结合因果特征的选择算法进一步定义与筛选任务分布中的有效特征[107],是提升强化学习可解释性与特征鲁棒性的可行方向.
3)为了提高强化学习的实用性,近年来研究者在交互模式上引入离线学习的设定,因为在一个大型离线数据集上能以更低的样本复杂度搜索目标任务的最优策略.但是,这类离线强化学习方法往往过于保守而存在鲁棒性较差的缺点[10].而且,这类方法在离线状态下存在准确策略评估的固有限制,使得它们在真实场景下的性能表现往往不及预期.因此,在离线设定下引入有限的环境交互,如专家交互,从少量交互资源中纠正策略偏差,进而改善离线强化学习先天缺陷,提升策略性能,是未来值得关注的方向.此外,理论上如何衡量离线数据集的多样性[74]和提供有限交互资源以实现对策略改进的性能保证,仍是理论研究中一个亟待解决的问题.进一步地,在应用方面,仍然缺乏一个可扩展且统一的基础框架,以便于在有限交互资源下整体评估各类算法的表现[95].
4)目前强化学习的研究方向主要针对单一难点,如分层强化学习主要解决稀疏收益的领域难点,但现实场景中往往存在多个难点,具有复杂的问题设定,因而需要更多复杂设定下验证多种方法组合性能的研究.例如,现实场景有稀疏的收益分布、收益函数难以设计、状态表示复杂三个难点,分别对应非平稳策略建模、未知收益函数学习、混杂状态空间的问题设定,因此可借鉴分层强化学习、逆强化学习和表示学习相关方法进行组合,并研究其组合的有效性与相关理论,如研究多智能体与稀疏收益设定下的有效性[108].进一步地,若解决方案追求多任务的泛化特性,结合元强化学习并维持方法的可扩展性是一个严峻的挑战.此外,多数场景具有较高的安全性要求,使用强化学习时如何维持多种特性之间的平衡也是未来研究的重要课题.

