基于萤火虫算法的螺栓连接结构布局优化

王长飞，周焕林

(合肥工业大学土木与水利工程学院，安徽合肥 230009)

0 前言

螺栓连接是机械结构中重要的连接方式，其连接强度直接关系到结构的安全性与可靠性。由于螺栓孔的存在，使得被连接件材料存在不连续性，极易产生应力集中、变形，甚至松弛脱落。为了减小连接板的孔周应力集中，使得连接结构载荷分布更为均匀，结构更加安全可靠，需要对螺栓连接结构的螺栓布局进行优化设计。KIM等介绍了4种不同的有限元模型，所提出的模型均考虑了预紧效应和连接件之间的接触特性，并通过试验对所提出的模型进行了验证。KWON等提出了3种模型来解决因接触面问题而难以建模的螺栓连接结构，并通过试验验证了模型的正确性。曹明利用ABAQUS分析软件通过7种建模方法对螺栓连接结合面进行了仿真和模态分析。吴松建、刘文光基于参数化模型，提出了一种螺栓连接板抗共振最优布局方法。PEDERSEN以螺栓的疲劳寿命为优化目标，对单个螺栓建立细节模型并进行了形状优化。XIA等在考虑疲劳寿命约束的条件下，对翼梁螺栓连接搭接板进行了优化设计。KRADINOV等将遗传算法和应力分析相结合，对螺栓搭接板中的螺栓直径、间隙、边距及间距等进行了优化设计，使得搭接板的最大应力显著下降。

本文作者以典型螺栓连接结构为研究对象，建立螺栓连接结构参数化有限元模型，分析了螺栓孔周应力，运用萤火虫算法以螺栓间距为优化变量对螺栓连接结构进行布局优化设计。

1 螺栓连接结构有限元分析

1.1 螺栓连接模型

研究对象为图1所示的多螺栓连接结构，由两块薄板和螺栓、螺母组成，螺栓为M12螺栓。该连接结构上端固定，下端承受20 MPa的面压荷载，使整个结构处于单剪的受力状态。其中螺栓连接结构的几何尺寸如表1所示。

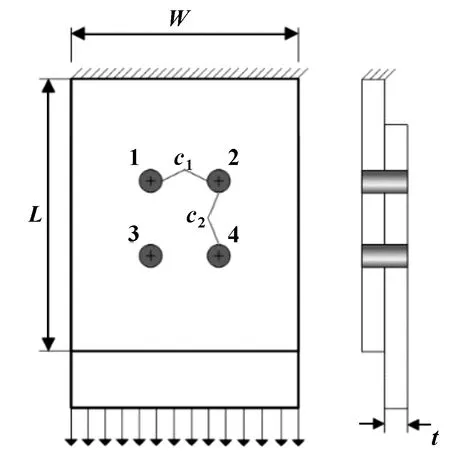
图1 螺栓连接结构示意

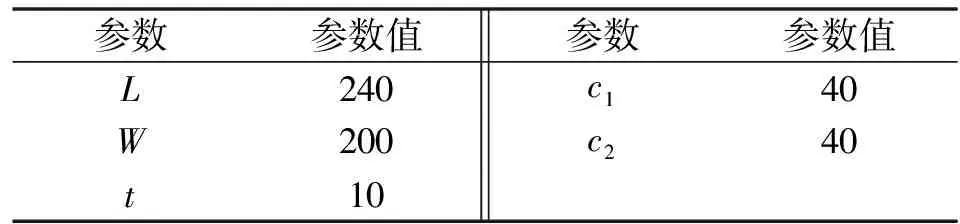
表1 螺栓连接结构几何尺寸 单位:mm

1.2 有限元建模

基于ABAQUS软件，将图1所示的螺栓连接结构模型离散化，所有单元均为六面体单元，考虑到连接板螺栓孔位置材料的不连续性，孔周属于应力集中区域，为了更好地模拟孔周应力集中现象，对螺栓孔进行网格细化，如图2所示。在螺栓连接结构中，螺栓预紧力和连接件之间的接触是螺栓连接的两个主要特性。在ABAQUS软件中，连接件之间的接触可以通过定义摩擦来模拟，预紧力可以通过施加螺栓载荷来模拟。

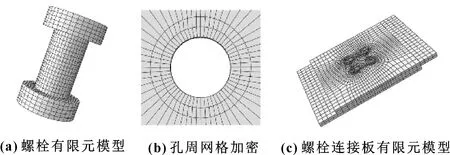
图2 螺栓连接结构有限元模型

考虑到ABAQUS软件所使用的内核语言是Python语言，可以利用Python语言编程对ABAQUS软件包实施二次开发，通过Python可以直接与ABAQUS内核交互，对螺栓连接结构进行参数化建模。

1.3 有限元分析

考虑到Von Mises等效应力能有效表示复杂载荷下连接板应力状态，以Von Mises等效应力不大于极限应力为设计标准。线性减缩积分单元(C3D8R)和非协调单元(C3D8I)都适用于接触分析，位移结果相近，考虑到C3D8I单元可以克服剪切自锁问题，得到的应力结果更准确，因此采用C3D8I单元进行螺栓连接结构的分析。

经过有限元计算，得到螺栓和连接板的应力云图，如图3和图4所示。可知：螺栓的最大应力为528.8 MPa，连接板的最大应力为376.6 MPa；第一排螺栓的孔周应力大于第二排螺栓，螺栓孔处有明显的应力集中，连接板的最大应力已超过设计极限，表明这个布局不合理，需要进一步优化。

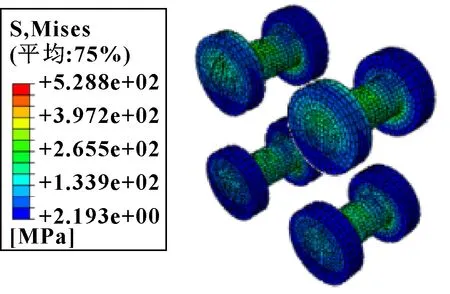
图3 螺栓应力

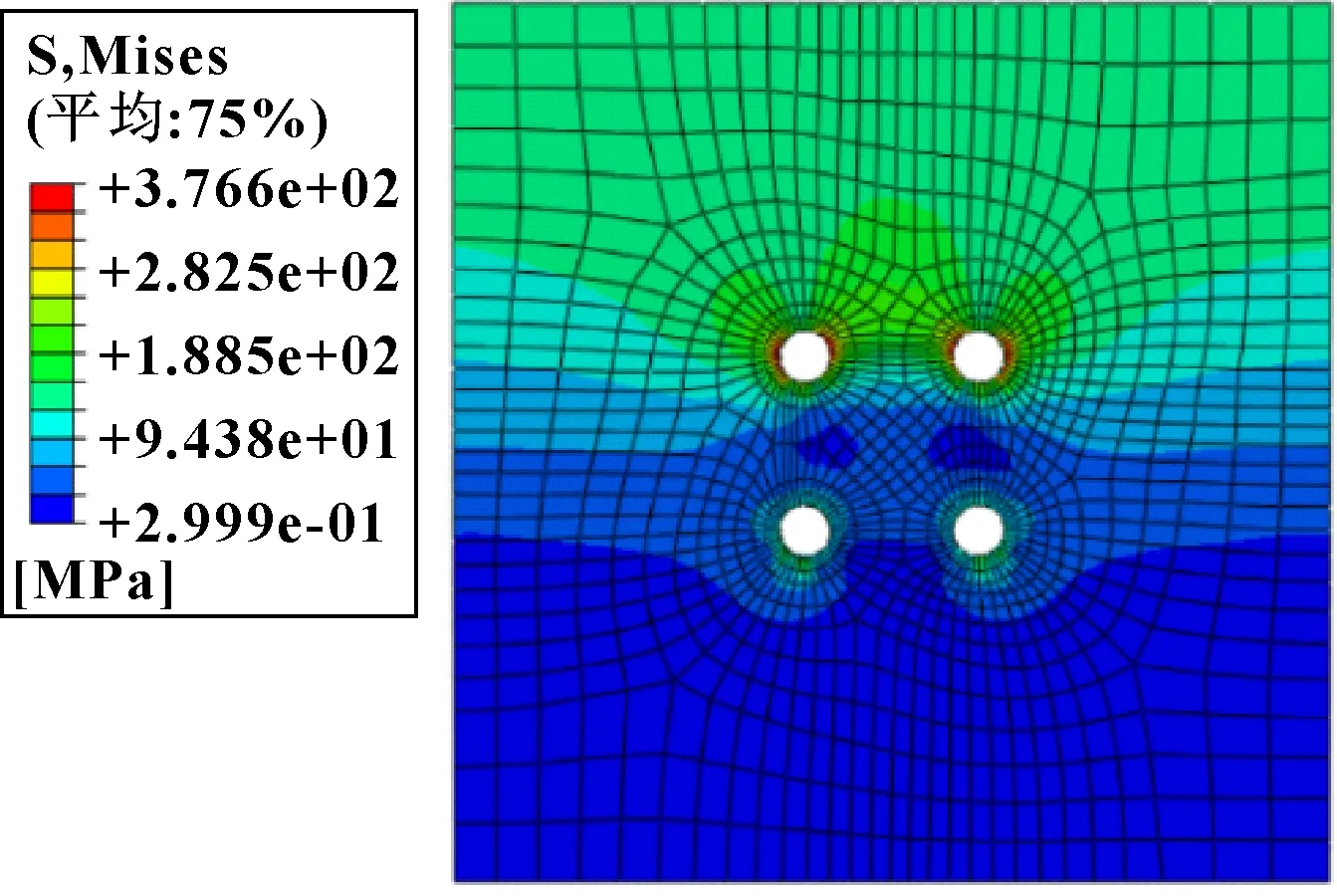
图4 连接板应力

2 萤火虫算法

2.1 萤火虫算法

萤火虫算法是由YANG提出的，它来源于对萤火虫群体行为的简化和模拟，是一种高级启发式算法。该算法通过萤火虫个体之间的相互吸引达到寻优的目的。假设待优化目标函数的解空间为维。在该解空间中，萤火虫算法随机初始化一群萤火虫、、…、、…、，为萤火虫的个数，是一个维向量，表示萤火虫在解空间中的位置，可以代表该问题的一个潜在解。定义萤火虫的绝对亮度是由目标函数直接决定的，则绝对亮度的大小直接表示了萤火虫所代表的潜在解的优劣，即绝对亮度更大的萤火虫所代表的潜在解更好。绝对亮度小的萤火虫被绝对亮度大的萤火虫吸引而不断向其移动，从而不断更新自身位置以找到最优解。

绝对亮度是指对于某只萤火虫，初始光强度(=0处的亮度)为萤火虫的绝对亮度，表达式为

=()

知识是核心素养的载体，活动是形成素养的途径。本节课通过具有思维性、实践性的教学活动，立足于学科方法与知识的渗透，促进核心素养的达成。

(1)

式中：()为优化模型目标函数。

相对亮度()是指萤火虫在萤火虫处的光强度，表达式为

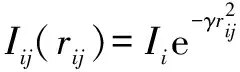
(2)

式中：为萤火虫的绝对亮度;为萤火虫到萤火虫的距离；为光吸收系数，可设为常数。

依据相对亮度可得到萤火虫对萤火虫的吸引力为

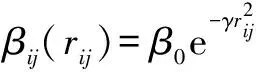
(3)

式中：为最大吸引力，即在=0处的吸引力，对于大部分问题，可以取1;为光吸收系数，可以取∈[0.01,100];为萤火虫到萤火虫的笛卡尔距离，即

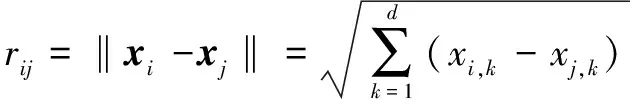
(4)

当萤火虫被萤火虫吸引后，萤火虫向其移动而更新自己的位置。位置更新公式如下：

(+1)=()+()[()-()]+α

(5)

式中：为算法的迭代次数；、为萤火虫和所处的空间位置；()为萤火虫对萤火虫的吸引力；为常数，取∈[0,1]；是由高斯分布、均匀分布或者其他分布得到的随机数变量。

2.2 螺栓布局优化

选取螺栓之间的横向间距和竖向间距作为优化变量，并以板的最大应力最小为优化目标，对螺栓连接件模型进行优化设计。根据钢结构设计规范，螺栓间距和边距应满足规范要求，对于M12螺栓而言，孔边距不应小于1.5，孔间距不应小于3。考虑到优化方案采用对称螺栓设计方案，当螺栓间距确定时，其边距也随之确定，因此设置螺栓间距大于36 mm、小于164 mm作为约束条件。

螺栓连接结构的布局优化可以由下式表示，

find,

min

s.t.≤,≤

(6)

式中:、为优化设计变量;和分别是设计变量的下界和上界；是连接板最大孔周应力。

3 螺栓布局优化结果

采用萤火虫算法对螺栓连接结构进行布局优化，优化后的连接板应力云图如图5所示。

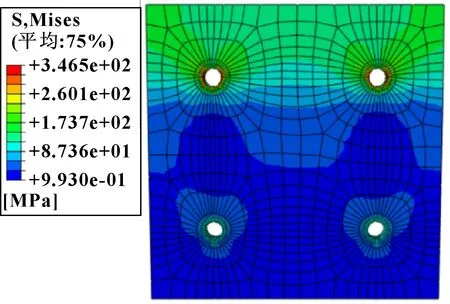
图5 优化后连接板应力

优化后螺栓最大应力为518.8 MPa，连接板的最大应力为346.5 MPa。优化后螺栓与连接板的应力均得到降低,优化结果如表2所示。可知:与原结构设计方案相比，优化后结构的最大孔周应力下降了30.1 MPa，优化率为8.0%。优化后连接板最大应力稍大于设计极限，考虑到可能由于螺栓数量较少，结构承载能力不足，现将螺栓数量由4个增加到6个，并对改变后的螺栓连接结构进行分析。

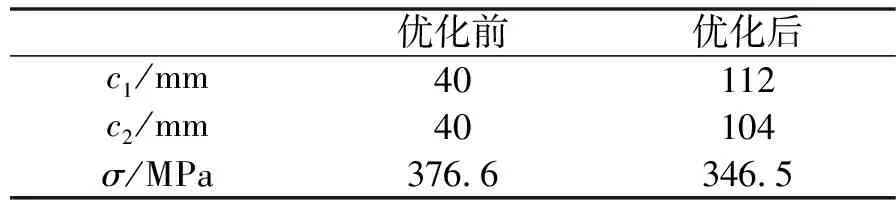
表2 优化结果(4个螺栓)

保持螺栓横向间距与竖向间距不变，将螺栓数量从4个增加到6个，此时连接件的螺栓初始设计方案有三排和双排两种，如图6和图7所示。

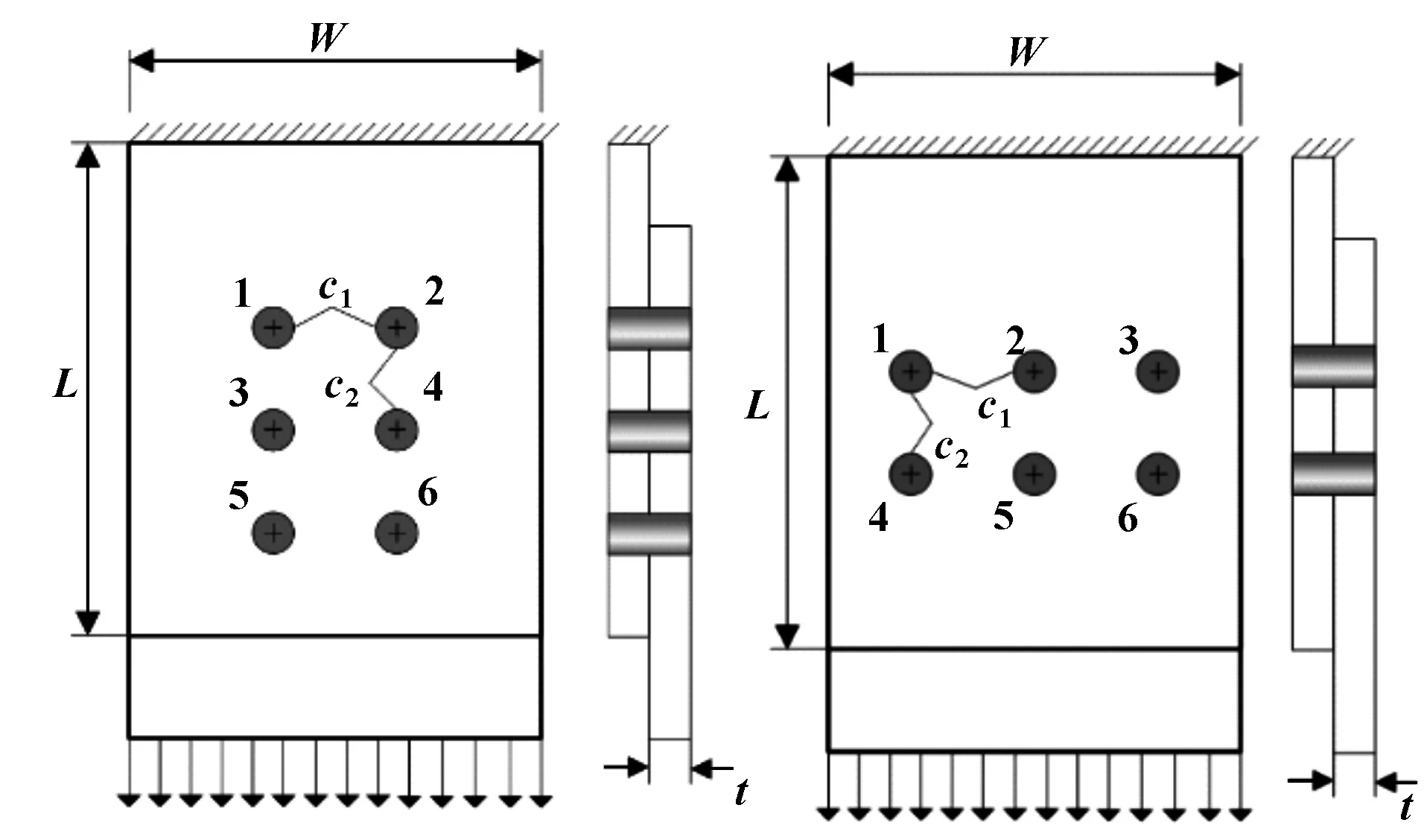
图6 三排螺栓连接结构示意 图7 双排螺栓连接结构示意

采用萤火虫算法对上述两种螺栓连接结构进行布局优化，优化后的螺栓连接结构如图8所示。可知：对于上述初始设计方案，优化后得到相同的螺栓布局。

图8 优化后螺栓连接结构示意

优化结果如表3所示。与第一种初始设计方案相比，优化后结构的最大孔周应力下降了67.1 MPa，优化率为20.5%；与第二种初始设计方案相比，优化后结构的最大孔周应力下降了23.6 MPa，优化率为8.3%。

表3 优化结果(6个螺栓)

由于结构对称，相同排螺栓孔周应力基本相同。沿螺栓孔逆时针方向提取优化前后连接板最大应力处的孔周应力进行对比，图9为优化前后最大孔周应力对比图。可知：优化前后，孔周应力集中位置基本不变，但孔周应力集中得到了明显改善。

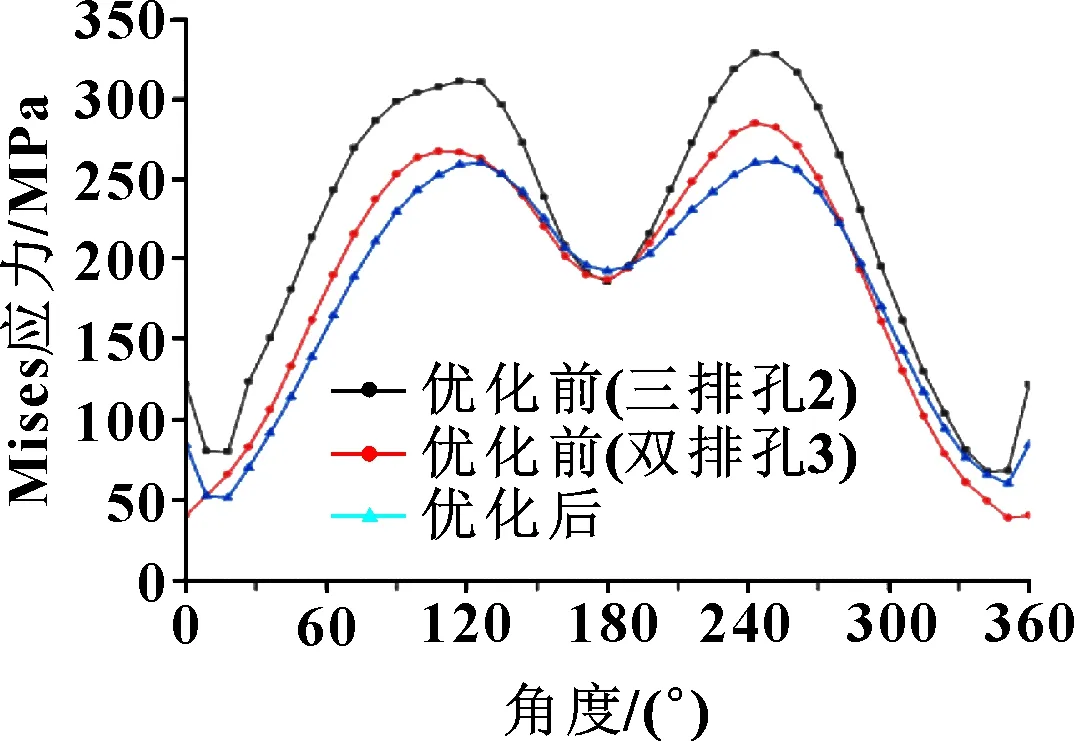
图9 优化前后最大孔周应力变化

4 结论

对螺栓连接结构进行力学分析，根据有限元计算结果，发现第一排螺栓的孔周应力大于其他排螺栓的孔周应力，相应地第一排螺栓的孔周应力集中也更加明显。将有限元方法与萤火虫算法相结合，对螺栓连接结构进行优化，螺栓数量为4个时，优化后结构的最大孔周应力下降了30.1 MPa，优化率为8.0%。螺栓数量增加后，对两种初始设计方案进行有限元分析。发现螺栓数量增加后连接板的孔周应力得到明显降低，但螺栓孔有严重的应力集中现象。对两种初始设计方案进行布局优化，得到相同的最优布局。与第一种三排螺栓的初始设计方案相比，优化后结构的最大孔周应力下降了67.1 MPa，优化率为20.5%；与第二种双排螺栓的初始设计方案相比，优化后结构的最大孔周应力下降了23.6 MPa，优化率为8.3%。

数值算例表明了萤火虫算法在螺栓连接结构布局优化中的有效性。研究结果可供机械设计参考。