基于优化极限学习机的涡轴发动机转子碰摩故障诊断
黄磊,戴金跃,胡阳,彭俞根
(1.江苏航空职业技术学院航空工程学院,江苏镇江 212134;2.中国航发北京航空材料研究院,先进高温结构材料重点实验室,北京 100095)
0 前言
涡轴发动机作为直升机动力源,无论在通航运输还是部队作战,其运行状态、工作环境都决定着飞行任务是否能够如期完成。由于涡轴发动机机动性能多变,飞行任务包线不如民航涡扇发动机规律,经常会在转子过渡态—稳态之间发生瞬间失衡现象,而这种现象会导致发动机出现短暂的碰摩现象。
目前,监控发动机转子状况,常采用分析安装在发动机机匣上各测点振动加速度传感器采集的振动信号的方法。但机匣测点上采集的振动信号通常属于耦合信号,需要对振动信号进行有效处理后,才能够有效识别出转子故障,而类似于短时傅里叶、小波变换等信号处理方法均存在一定的局限性。因此,部分振动信号的故障诊断采用振动信号分析与诊断算法相结合的方法。
针对涡轴发动机出现的碰摩故障,MUSZYNSKA、袁惠群、褚福磊、WILLIAMS等学者的研究,使得转子碰摩实现从原理分析到数学求解、从有限元仿真到实物模拟,并到工程应用。随着碰摩理论的深入研究,针对不同情况而进行的碰摩研究较多。王四季等以对转双转子局部碰摩为研究对象,对高压、低压、高低压转子碰摩进行实验分析,并通过频谱分析得出碰摩故障能够通过和频进行诊断。但对于基于振动信号分析的识别方法,如果事先未知故障频谱特征成分表现形式,则难以进行故障识别。因此,本文作者针对某涡轴发动机涡轮机匣振动测点采集的数据,对频谱进行分析,提取振动特征参数,结合优化极限学习机,对涡轴发动机燃气涡轮碰摩、动力涡轮碰摩等状态进行识别。
1 极限学习
极限学习机(Extreme Learning Machine, ELM)网络通过随机产生输入层与隐含层的连接权值和阈值,并基于Moore-Penrose算法计算极限学习机网络的输出,实现了避免单隐层前馈神经网络的缺陷,因而广泛用于数据压缩、特征学习、聚类、诊断等领域。HUANG等对极限学习机理论进行严格的数学论证,表明它能够逼近任意的非线性分段函数。
假设有个独立样本(,),=[1,2,…,]∈、=[1,2,…,]∈,具有个隐含层节点且隐含层与输出层激活函数分别为()、()的单隐层前馈神经网络结构如图1所示,数学表示如式(1)所示。

图1 极限学习机网络结构
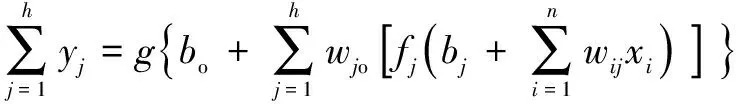
(1)
式中:为输入变量,=1,2,3,…,;为输入变量与隐含层神经元的连接权值;o为隐含层神经元与输出层的连接权值;为隐含层神经元的阈值,=1,2,3,…,;为输出层神经元的阈值。
如果为0,且()为线性激活函数时,将个独立样本代入式(1)简化可得式(2):
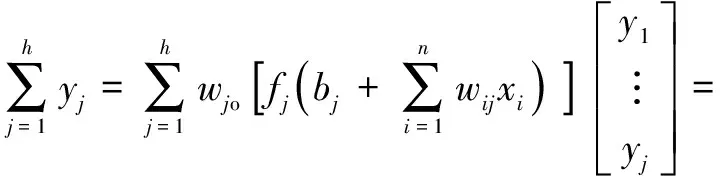

(2)
==⟹=
对于式(2),如果存在观测样本,同时∈×、≥且()=,则的Moore-Penrose广义逆可表示为
=()
(3)
将式(3)代入式(2)可得出极限学习机输出权值向量:
==()
(4)
极限学习机中常用的激活函数有几种,文献[9,12]对不同激活函数进行了研究。本文作者基于这些文献研究结果,选择Sigmoid()函数作为激活函数。
2 优化的极限学习机
极限学习机能有效避免部分前馈神经网络存在的缺陷,但它相比其他网络可能需要更多神经元。同时,其随机权值的赋予,可能会导致病态问题的产生,故采用遗传算法进行优化。
遗传算法的诞生得益于生物基因间的变异、交叉、选择,是一种被广泛应用于不同行业的智能寻优算法。随着遗传算法的不断应用,也逐渐暴露出搜索能力受交叉变异概率影响等缺陷。因此,本文作者采用改进遗传算法对极限学习机进行优化,并运用到后续转子故障诊断。
2.1 遗传算法
遗传算法中基因个体的选择沿用轮盘赌方式执行,假设个体累积概率为、个体适应度函数为()、轮盘旋转次数为,则个体累积经验选择概率可表示为

(5)
在遗传算法中,变异操作能改变种群个体的结构,是影响遗传算法搜索的关键。因此,应在保证种群多样性的同时提高算法搜索能力。本文作者借鉴文献[14]中的方法引入高斯变异,采用如式(6)所示的变异操作方式:
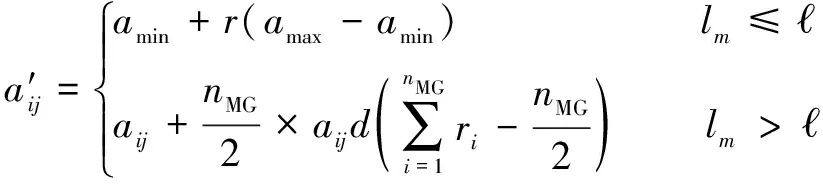
(6)

=min{-,-}
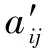
交叉、变异操作均采用多点方式进行(每次变异点数为当前基因数的50%,变异位置随机选择),其操作示意分别如图2、图3所示。

图2 多点交叉
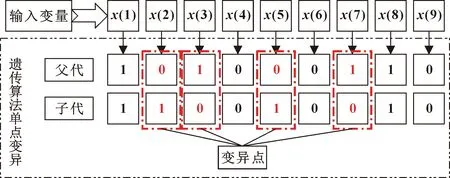
图3 多点变异
2.2 优化的极限学习机
优化的极限学习机是采用遗传算法优化极限学习机中隐含层神经网络的权值和阈值。优化的极限学习机主要分为两部分:一部分是遗传算法根据个体适应度,不断进行个体基因交叉、变异、选择,每次迭代更新过程中需要更新最优个体,迭代结束后最优个体基因序列值即为极限学习机中隐含层神经网络的权值和阈值;另一部分是极限学习机部分,极限学习机在接收到每次迭代更新的最优个体时,计算当前个体下输出权值和适应度函数,并将结果反馈给遗传算法,用于遗传算法迭代计算。优化极限学习机流程如图4所示。

图4 优化的极限学习机流程
优化极限学习机诊断流程描述如下:
(1)基于待诊断数据样本类型确定ELM网络的结构,并定义遗传算法种群适应度函数;
(2)初始化遗传算法基本参数,并对种群中个体的基因序列值进行二进制编码;
(3)对种群进行交叉、变异、选择操作,产生新的个体,即可行解;
(4)将所得到的可行解代入极限学习机中,通过Moore-Penrose方法计算ELM网络输出权值矩阵,并计算当前个体适应度,遍历整个种群找到局部最优解,并更新全局最优解;
(5)算法终止判断:若满足算法终止条件,则输出遗传算法全局最优解,并代入极限学习机中;若否,则重复步骤(3)—步骤(5);
(6)用Moore-Penrose方法计算极限学习机输出权值矩阵,并对故障样本进行诊断。
3 转子碰摩实验
3.1 转子碰摩数据来源描述
涡轴发动机转子振动碰摩数据源自某型号军用发动机,由于信息保密的原因,以发动机涡轮机匣测点为碰摩振动监测点,从涡轴发动机试车数据中提取并稍加处理动力涡轮、燃气涡轮转子的0.5、1、2、3、4倍频,进而构建涡轴发动机的振动包络曲线,经过处理后的发动机正常状态包络线幅值如图5所示。以图6所示的试车转速曲线(燃气涡轮最大转速为36 700 r/min、动力涡轮为25 400 r/min)还原振动信号,涡轮机匣测点的采样频率为10 kHz,模拟时间为3 min。模拟振动信号包括涡轴发动机正常状态、燃气涡轮转子碰摩、动力涡轮转子碰摩、燃气与动力涡轮碰摩4种,碰摩故障发生点都在转子转速达到最大转速后0.02 s处。

图5 振动包络曲线

图6 转速曲线
3.2 转子碰摩振动信号分析
涡轴发动机发生碰摩段的燃气涡轮转子转速为36 700 r/min、动力涡轮转速为25 400 r/min,各基频幅值分别为611.7、423.3 Hz,分别记为、。涡轴发动机正常状态、燃气涡轮转子碰摩、动力涡轮转子碰摩、燃气与动力涡轮碰摩4种状况的振动信号和快速傅里叶变换(Fast Fourier Transform,FFT)频谱如图7所示。可知:正常状态与碰摩故障状态下的振动信号、频谱信号存在较明显差异,碰摩状态更加凸显次谐波的存在;但对于另外3种碰摩状态,从振动信号上而言,不存在明显的区别,但频谱图却存在较为明显差异,频谱中均存在主频、次频、和频成分;基于文献[8]中的结论,根据和频的出现可判断碰摩故障的发生。
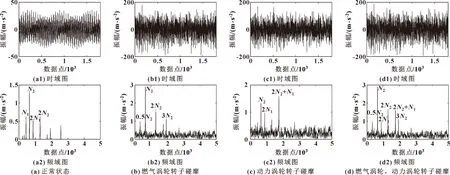
图7 转子碰摩振动信号分析
3.3 转子碰摩数据提取与处理
由图7可知,如不具备对碰摩故障信号的分析经验,难以从振动信号或频谱信号中直接分析出碰摩故障或碰摩故障类型,但碰摩故障特征会表征在振动信号的特征指标中。因此,本文作者提取振动信号的偏度指标、均方根指标、波形指标、脉冲指标、峰值指标、裕度指标,并基于第2节提到的优化极限学习机对碰摩故障进行诊断。
每类工作状态下数据集均为120组,共计480组数据,部分数据如表1所示。可以发现:不同状态下的碰摩故障所引起的特征指标变化趋势存在差异,且各指标之间数量级差异明显,容易增加数据级所导致的诊断误差,因此按式(7)进行归一化处理:

表1 特征指标数据集

(7)
其中:、和分别表示特征指标的最大值、最小值和平均值;表示特征指标的第个值;表示归一化后的值。
4 转子碰摩故障诊断
基于第3节得到的转子碰摩数据,采用文中提到的优化极限学习机模型对碰摩故障类型进行诊断。算法参数设置:遗传算法种群大小为30、迭代步数200、种群范围为[-0.5 0.5];极限学习隐含层神经元个数由后续实验结论予以确定。为避免诊断结果不受初始数据随机性的影响,诊断实验重复50次,取平均值为结果。
4.1 数据比例分配与输出结果描述
诊断过程中,随机将480组样本打乱,用于训练、校验、测试的样本比例为5∶3∶2,且样本数据间彼此不重复。由于神经网络输出神经元判断类型均采用概率表示,为避免分类出现小数等特殊情况,对网络输出结果采取四舍五入法,直接转换为故障类型标签,予以识别。
4.2 ELM网络神经元参数选择
由于极限学习机的隐含层神经网络数量对诊断结果存在影响,需要基于数据样本进行实验,选择合适的神经元数量。训练集、测试集诊断准确率与校验集误差收敛值随极限学习机隐含层神经元数量的变化如图8所示。

图8 诊断准确率、校验集收敛误差与ELM隐含层神经元数量的关系
由图8可知:随着神经元数量逐渐增加,训练集、测试集诊断准确率逐渐增加,神经元数量较少时诊断效果差,收敛误差波动范围较大。通过综合分析,诊断算法中隐含层神经元数量设定为114,因为此时训练集、测试集诊断准确率相对较高,误差收敛值较稳定,不会出现训练集准确率增加而测试集诊断结果降低的过拟合现象。
4.3 诊断结果描述
优化极限学习机对转子碰摩故障的诊断结果如图9所示。可知:在50次诊断过程中,训练集样本准确率为95%~98%,平均准确率高达96.8%,诊断准确率最大波动幅值为2.82%(如图10所示);测试集诊断准确率处于95%~95.93%,平均准确率高达95.43%,诊断准确率最大波动幅值为0.93%(如图11所示)。在诊断过程中,算法的平均收敛误差如图12所示,其误差收敛趋势平滑下降,且能够达到0.22的收敛精度。
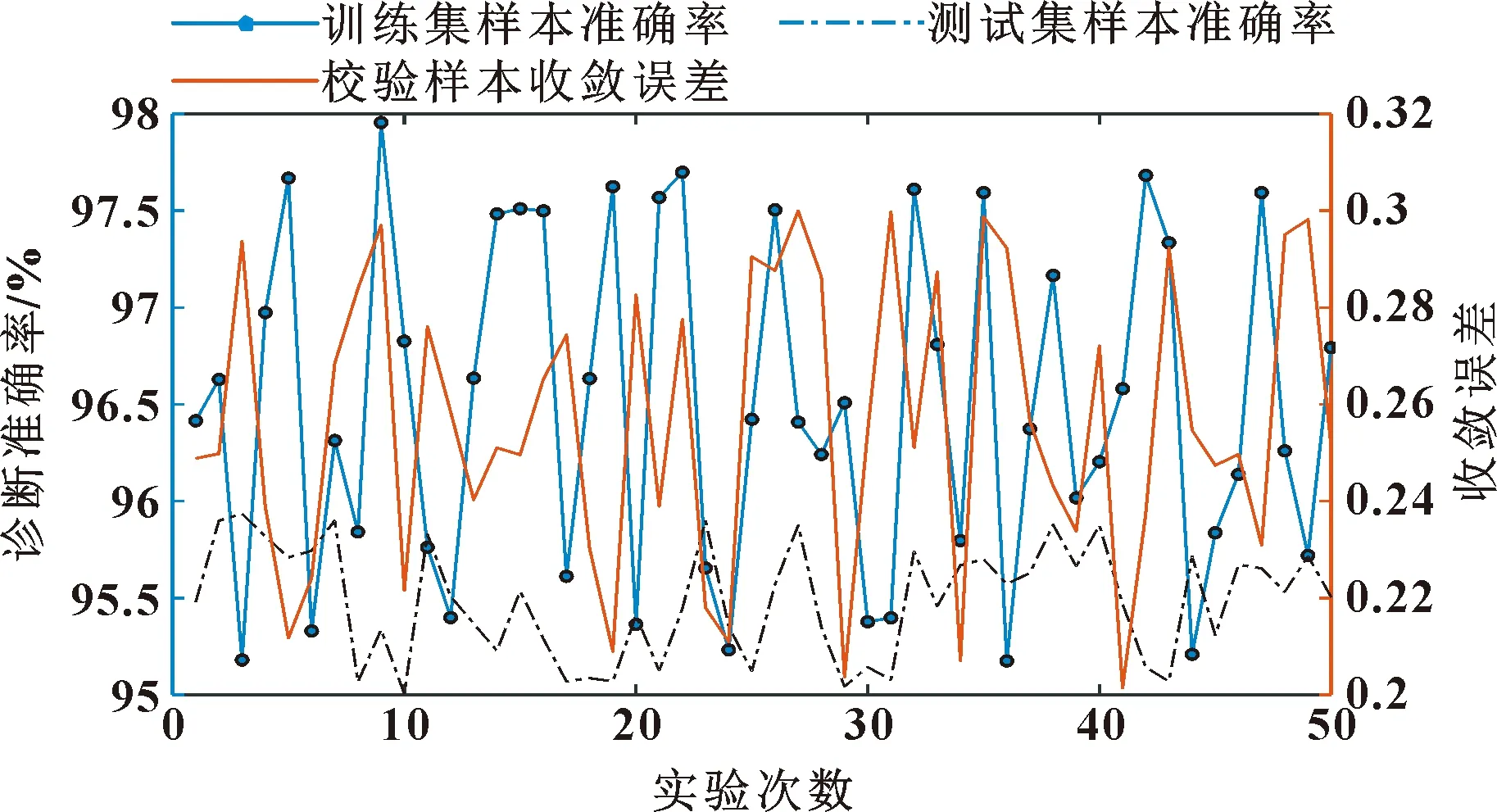
图9 优化极限学习机50次诊断结果

图10 训练集诊断结果波动情况 图11 测试集诊断结果波动情况 图12 校验集平均误差收敛情况
由上述分析可知,基于优化极限学习机的转子碰摩故障诊断在多次诊断下,其诊断效果明显、结果波动幅值较小,收敛误差相对较低。因此,优化极限学习机适用于转子碰摩故障诊断。
5 总结
针对涡轴发动机转子出现碰摩的情况,本文作者提出了优化极限学习机的碰摩故障诊断方法。首先,基于某实际涡轴发动机振动包络曲线,还原涡轴发动机正常状态、燃气涡轮碰摩、动力涡轮碰摩以及燃气动力涡轮碰摩4种状况下的振动信号,并对振动信号进行频谱分析,得出不易从振动信号频谱中识别出故障的结论;其次,提出基于振动信号特征的数据集,可使用优化的极限学习机对它进行诊断;最后,进行了仿真实验。结果表明:优化极限学习机诊断准确高达95.43%,诊断结果波动幅值为0.93%,收敛误差相对较低,验证了优化极限学习机适用于转子碰摩故障诊断。

