二阶同步提取Chirplet变换及应用于变转速滚动轴承故障诊断

柯伟，金仲平，吕信策，余肇鸿

(1.台州市特种设备检验检测研究院，浙江台州 318000；2.武汉科技大学机械与自动化学院，湖北武汉 430081)

0 前言

旋转机械被广泛应用于众多领域中，而滚动轴承在旋转机械中起着至关重要的作用，同时也是最常见、最主要的故障来源之一。当轴承发生故障时，相应的故障特征会表现在振动信号中，因此对振动信号进行故障特征提取即可有效地对滚动轴承进行故障诊断。但是旋转机械的传动系统十分复杂，振动信号通常被淹没于背景信号与噪声中，难以被准确识别。并且，在实际工业生产中，设备往往是以变转速的运行状态工作，此时滚动轴承的故障信号为非平稳信号，传统的故障特征提取方法无法准确识别其故障特征。因此，能够揭示信号非线性时变特征的时频分析方法(Time-Frequency Analysis，TFA)开始为国内外学者关注。

常见的时频分析方法包括：短时傅里叶变换(Short-Time Fourier Transform，STFT)、Chirplet变换(Chirplet Transform，CT)、连续小波变换(Continuous Wavelet Transform，CWT)等。STFT是通过窗函数将信号切分成许多相同的小的时间间隔，近似认为每一个时间间隔内的信号是平稳信号，用傅里叶变换(Fourier Transform，FT)分析每一个时间间隔，以此来确定该时间间隔存在的频率。但由于STFT是一种线性固定分辨率的时频分析方法，受Heisenberg-Gabor不等式的约束，对复杂信号进行时频分析的效果较差。连续小波变换(CWT)利用一个小波函数在局部时间窗口内与信号相乘，具有多分辨率、局部性好等优势，但其窗口仍是相对固定的，不能够根据信号特征调节窗口参数。CT是一种具有较高分辨率的参数化时频分析方法，采用变换核函数，通过一个额外的调频参数，使之能更好地匹配待分析信号，达到更优的时频分析效果。

传统时频分析方法自身存在一些不足，无法满足高分辨率的需要，这就需要对它们进行改进。为实现理想时频表达，借鉴同步压缩变换(Synchrosqueezing Transform，SST)算法思想，YU等提出一种新的时频分析方法，并命名为同步提取变换(Synchroextracting Transform，SET)。与SST的压缩方式不同，SET方法仅保留与信号瞬时频率(Instantaneous Frequency，IF)有关的时频信息，并去除大部分模糊能量。尽管SET可以增强能量集中度，但是由于SET依赖于恒定振幅和线性频率调制信号的假设，在分析强调制信号时，很容易偏离真实的IF时频脊线。ZHU等对SET算法进行了改进，借鉴CT变换的思想，提出SECT算法，并进行了验证，得出SECT较SET确实有一定改进，但时频面上的能量不够集中，同时与SET一样易受噪声影响，计算结果的时频面上仍具有较多噪声成分。BAO等推导了二阶SET算法，通过对STFT求二阶偏导数，能够更好地实现瞬时频率的估计，进而使得计算结果更加接近IF曲线，但由于STFT本身受到固定窗宽的影响，其应用前景有限。

基于此，本文作者基于STFT的标准SET算法进行了理论分析；考虑到STFT受到窗宽的局限性，基于Chirplet变换推导同步提取Chirplet变换(SECT)理论，可以有效地改善时频表达；利用相位的二阶展开进行更准确瞬时频率估计，进一步提高时频脊线的能量集中性，提出二阶同步提取Chirplet变换算法。利用模拟信号说明SECT2在应用中具有更好的时频聚焦性。利用蝙蝠信号与变转速试验台数据对所提方法进行验证，并实现变转速下轴承故障诊断。

1 理论描述

1.1 同步提取理论

标准SET算法基于STFT时频谱估算瞬时频率，设多分量AM-FM信号()的数学模型为

(1)

(2)

其中：()为Schwartz空间中的窗函数，定义为标准偏差的高斯窗函数：

(3)

基于STFT的标准SET写成：

(4)

(5)

[-(,)]为同步提取算子(SEO)，满足以下条件：

(6)

基于STFT的SET算法框架如图1所示。由于STFT受到Heisenberg-Gabor不等式的约束，导致它进行瞬时频率估算的结果不准确。因此,本文作者对基于CT时频谱的IF估算展开研究。

图1 标准SET算法框架

1.2 同步提取Chirplet变换

由于STFT窗函数选定之后，分辨率无法改变，CT通过使用额外的参数调频率(Chirp Rate，CR)进行窗口调节。对于信号()，其CT定义为

(7)

其中:为CR参数。假设在=附近，信号()的相位近似等于其二阶局部展开：

(8)

同样，考虑幅值调制定律在=附近的展开，即：

(9)

其中:为一个正整数;()为()的阶导数。

基于式(8)(9)的假设，若≡″()，式(7)可以改写为

(10)

则基于CT进行的瞬时频率IF估计公式写为

(11)

(12)

因此，SECT算法定义为

(13)

1.3 二阶同步提取Chirplet变换

基于CT，式(1)定义信号()的理想时频表示(ITFR)描述为

(14)

通常，假设单分量信号在每个瞬间都被高斯调制：

()=e[(-)](2)ei2π(++12)

(15)

基于此假设，信号()对的导数可以写成：

(+)()

(16)

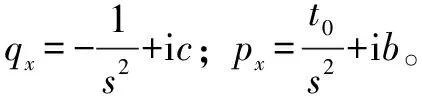
(17)

(18)

结合式(17)和式(18)，得到：

(19)

因此，对瞬时频率IF即′()的二阶估计可描述为

′(,)=(+)

(20)

其中:()表示复数的虚部。

最终，文中所提出的二阶同步提取Chirplet变换(SECT2)定义为

(21)

其中：[-′(,)]为二阶同步提取算子。文中所提出方法的整体流程如图2所示。

图2 文中方法的流程

2 数值仿真信号分析

在噪声背景下，时频分析方法可以有效识别时变特征，正确提取不同组分的时频脊线，即表明它具有良好的适用性。文中数值模拟仿真各组分信号设置如下：

()=e-003cos[2π(007-08+4+25)]

(22)

()=e-003cos[2π(014-16+8+50)]

(23)

()=e-003cos[2π(021-24+12+75)]

(24)

()=()+()+()+()

(25)

对模拟信号添加信噪比为15 dB的噪声()，信号时域图如图3(a)所示，模拟信号的理想IF曲线如图3(b)所示。

图3 模拟信号时域图及其理想IF曲线

分别使用STFT、CT的时频分析方法对模拟信号进行分析，其计算结果如图4所示。相比于STFT，CT的计算结果具有更高的时频能量聚焦性，因此对CT进行进一步研究。

图4 STFT及CT计算结果(数值仿真信号)

对SET算法进行改进，将原有基于STFT的SET算法改为基于CT的SET得到SECT算法。SET、SECT的计算结果如图5所示。

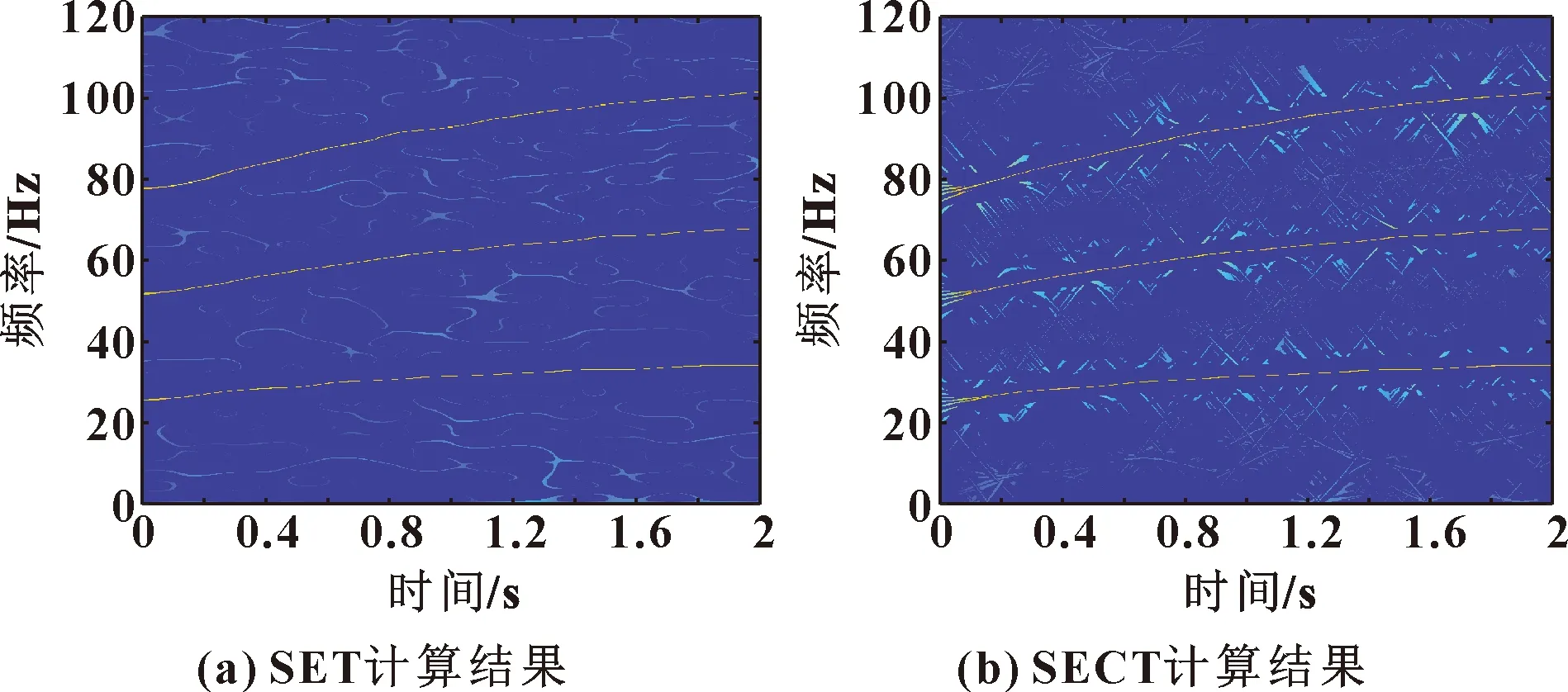
图5 SET及SECT计算结果(数值仿真信号)

由图5可以发现：无论是SET还是SECT，噪声对时频表达分辨率均有较大影响，存在不同程度的时频模糊现象。对比图3(b)，图5均不能获得理想的时频表达，存在着时频脊线能量发散甚至脊线扭曲失真的问题。为增强时频聚焦性，进行更加准确的瞬时频率估计，利用文中所提出的SECT2算法对数值仿真信号进行分析，结果如图6所示。

图6 SECT2计算结果(数值仿真信号)

通过观察以上几种方法的计算结果，SECT2计算的结果时频聚焦性最好，且脊线能量较高，脊线形状与图3(b)所示理想IF曲线最符合。各种方法的Renyi熵对比如表1所示。Renyi是一种衡量时频面能量聚集程度的指标，其值越低表明该处理结果脊线的能量越集中，SECT2方法的时频处理结果具有最集中的能量，验证了所提方法具有较好的有效性与先进性。

表1 几种方法计算结果的Renyi熵比较(数值仿真信号)

3 试验数据分析

3.1 蝙蝠信号分析

以莱斯大学(Rice University)记录的蝙蝠信号为例，该信号的采样频率为140 kHz，时域图、频谱如图7所示。对它进行STFT、CT计算，结果如图8所示。两种时频处理方法能量均过于分散，但相比之下CT方法计算结果比STFT方法计算结果好。

图7 蝙蝠数据时域图及频谱

图8 STFT及CT计算结果(蝙蝠信号)

在STFT、CT方法的基础上，利用SET、SECT方法对蝙蝠信号进行处理，结果如图9所示。可知：SECT能量发散，不能很好地反映多组分信号时频脊线。利用SECT2方法对蝙蝠信号进行处理，结果如图10(a)所示，显然其时频能量的聚集性更好。

图9 SET及SECT计算结果(蝙蝠信号)

对SECT2计算结果作脊线提取，结果如图10(b)所示，可知所提出方法能够较好提取蝙蝠信号中包含的脊线信息。表2所示为几种方法的Renyi熵值比较，结果表明SECT2方法计算结果的时频面上噪声干扰信息较少，具有更好的多组分信号时频分析能力。

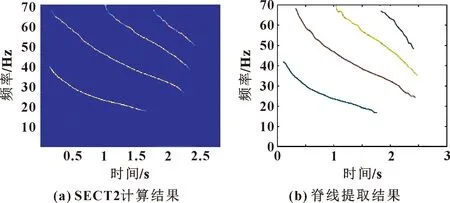
图10 SECT2计算结果及其脊线提取结果

表2 几种方法计算结果的Renyi熵比较(蝙蝠信号)

3.2 试验台故障数据分析

为验证所提出的SECT2方法的有效性，以实验室轴承-齿轮故障综合试验台进行测试和分析。试验台及其结构简图如图11所示，其中测点处为可更换的故障轴承，轴承故障类型为外圈故障。为模拟变转速工况，试验转速从0加速到1 000 r/min，并经过一段时间恒转速运行，最终减速到0，采样频率设置为2 560 Hz。测量得到的原始振动信号时域图及频谱如图12所示。

图11 试验台实物图及其结构简图

图12 试验台振动信号时域图及频谱

由于试验台模拟变转速工况，从图12(b)中的频谱图中无法反映出时变的故障特征信息。对采集的信号作STFT及CT分析，结果如图13所示。可知：STFT的时频模糊现象很明显，噪声随机地分布于时频平面，无法正确识别时变故障特征；相比之下，CT的结果较好，其时频脊线的能量较高，但仍然很发散，难以进行脊线提取。利用所提出的SET及SECT对振动信号进行分析，结果如图14所示。

图13 STFT及CT计算结果(试验台信号)

图14 SET及SECT计算结果(试验台信号)

对比计算结果可知：SET、SECT方法时频表达效果较STFT和CT有所提升，但依然存在时频脊线能量不集中问题，在100～150 Hz之间有严重的能量发散现象，无法从时频图中有效地识别故障特征，导致时频分析的效果欠佳。利用所提出的SECT2方法进行进一步处理，使其时变信号的能量进一步集中，相应的处理结果如图15所示。

图15 SECT2计算结果(试验台信号)

对比图14和图15可知，SECT2方法处理结果相比于SET和SECT，其时频表示的分辨率明显增强，时频脊线更加集中，且有效地解决了能量发散问题。上述几种方法的Renyi熵比较如表3所示。可知：SECT2具有最小的Renyi熵，说明它具有最高能量的时频脊线，且能量集中程度最佳。

表3 几种方法计算结果的Renyi熵比较(试验台信号)

对SECT2方法处理结果进行脊线提取，结果如图16所示。从图中可以很清晰地识别到故障特征频率及其2倍频。通过安装转速传感器，实际测量得转频曲线为0递增到16.6 Hz，再递减至0。根据图15中提取的故障特征频率曲线为0递增到53 Hz，再递减至0，故障特征频率(FCF)曲线为转频曲线的3.2倍。根据轴承动力学特征，利用外圈故障计算公式：=04××=3.2，可以判断故障为轴承外圈故障，验证了所提方法对变转速下轴承故障诊断的有效性。

图16 SECT2方法脊线提取结果

4 结论

基于同步提取理论，本文作者结合Chirplet变换，推导同步提取Chirplet变换公式，进一步地，对瞬时频率进行二阶估计，提出了二阶同步提取Chirplet变换，用于实现噪声干扰下的多组分信号高分辨率表达。与基于STFT的标准SET进行了对比，所提出的SECT2具有更强的时频脊线聚焦性，可获得比SET更集中、更高能量的时频脊线。通过蝙蝠信号、试验台测量信号对所提方法进行验证，结果表明SECT2方法具有更好的时频分析能力。