环形防喷器密封胶芯本构模型研究

王玥,邹龙庆,张宗旭,付海龙,2,黄聪聪

(1.东北石油大学机械科学与工程学院，黑龙江大庆 163318；2.东北石油大学环渤海能源研究院，河北秦皇岛 066004)

0 前言

在石油天然气钻采装备中，橡胶材料充当重要的密封元件。环形防喷器密封胶芯为丁腈橡胶材料，其弹性和密封能力决定了环形防喷器井控能力。环形防喷器的工作环境较为复杂，密封胶芯作为其核心部件，会受到高温、过载等各种极端工况，这些对其密封性能形成考验。近年来，越来越多的人通过数值模拟对橡胶密封性及力学性能展开研究。橡胶力学行为较复杂，力学性能会随环境温度、加载历程和材料成分等条件的不同而不同。材料本构模型的确定作为力学研究的关键显得尤为重要。按照连续介质力学观点，橡胶属于典型的超弹性材料，其非线性高弹特性用超弹性模型来表征。为此，基于应变能函数的超弹本构关系确定成为环形防喷器密封胶芯力学分析的前提。

目前针对橡胶主要有基于黏弹性描述的Maxwell模型和Kelvin-Voigt模型，基于超弹性描述的Neo-Hookean 模型、Mooney-Rivilin模型和Yeoh 模型。Maxwell模型优势在于表征黏弹性材料的松弛现象，而不能表征蠕变；相反，Kelvin-Voigt模型只能表征材料的蠕变，表征应力松弛方面具有短板。因此这两种模型均不能准确地反映防喷器胶芯的力学性能。而由上述两个模型演绎的多元组合模型广义Maxwell模型虽然能够较好地反映橡胶材料的力学性能，但由于引入参数较多，方程过于繁杂，且各弹性和黏性单元的参数识别比较困难。按超弹材料理论的Neo-Hookean模型描述大应变时不够精确，且使用范围较窄。而Yeoh模型在描述小应变能函数时，需要引入较多参数，从而降低了有限元分析过程中的适用性。Mooney-Rivilin模型因能够在较大变形范围内描述橡胶材料的力学性能，且采用双参数描述方式，模型更简单，因此在工程上被广泛应用。

本文作者提出通过橡胶单轴压缩实验构建橡胶材料应力应变关系，并经最小二乘法拟合，建立Mooney-Rivilin本构关系，其可靠性经数值分析和有限元计算获得验证。

1 丁腈橡胶Mooney-Rivilin 模型参数

Mooney在Rivilin应变能函数的基础上简化得到Mooney-Rivilin本构模型，其应变能为

=(-3)+(-3)

(1)

式中:、为材料参数。

根据能量守恒定律，有限变形弹性固体的本构模型：

=-++

(2)

其中:为柯西(Cauchy)应力张量；为反映为左Cauchy变形张量。、分别定义为

(3)

(4)

初始无应力构型的超弹性材料，应变能函数可表示为

=(,,)

(5)

(6)

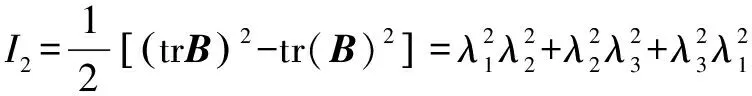
(7)

(8)

其中：为左Cauchy变形张量的第三不变量；、、为3个主伸长比。

由于橡胶材料的变形过程在受力方向上各向同性且不可压缩，故：

(9)

应力张量可表示为

(10)

如图1所示，取一橡胶微元，当3个方向的正应力都不为零时，称该点处于三向(空间)应力状态，如图1(a)所示；而对于单轴压缩实验，只有一个方向受力，另外两个方向自由，如图1(b)所示。所以有：

图1 不同工况下橡胶微元主应力分布

==0

(11)

(12)

将式(12)代入式(10)中，可得：

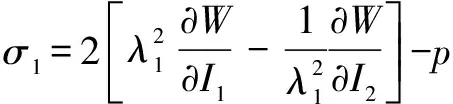
(13)

(14)

令=，联立式(13)、(14)可得：

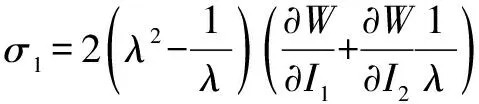
(15)

因此有：

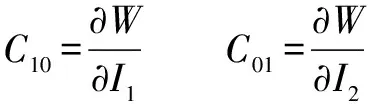
(16)

故有：

(17)

在单轴压缩实验中，主应力方向上的工程应变与主伸长比的关系为

=1+

(18)

主应力与工程应力的关系为

=

(19)

因此，应力应变的关系为

(20)

2 橡胶压缩实验

2.1 实验方法及过程

实验所用橡胶试件为丁腈橡胶，其直径=30 mm，高度=10 mm，邵氏硬度85,如图2所示。

图2 实验用橡胶试件

实验准静态加载采用的CMT5105型全数字化电子万能试验机如图3所示。将试件置于实验台下托盘中心并与上压板对中，启动试验机，上压板以10 mm/min的速度施压橡胶试件。加载遵循GB/T 7757—2009《硫化橡胶或热塑性橡胶压缩应力应变性能的测定》,压缩最大应变量25%。

图3 丁腈橡胶试件单轴压缩实验系统

正式实验之前对所有橡胶试块进行预实验，每次以10 mm/min的速度施压橡胶试件，直至应变达到25%，卸载使试件回弹5 min，目的是为了消除Mullins效应对实验结果的影响。正式实验共有3组，3个尺寸材料完全相同的丁腈橡胶试块以相同的速度压缩至相同的变形量，每组实验进行多次重复测试。计算机自动记录3组实验的力-位移对应数值，由数值获得的其中1组力-位移曲线如图4所示。

图4 单轴压缩力-位移曲线

2.2 实验结果分析

经多组重复性实验，选取有效实验结果取均值并分别计算应力和应变。建立的应力-应变曲线如图5所示。可见，在加载阶段应力-应变近似线性关系，而在卸载过程中应变明显滞后于应力且变形恢复具有一定的迟滞，验证了橡胶在小变形压缩阶段具有线弹性特征，但变形恢复过程具有明显的黏弹性特征。

图5 单轴压缩应力-应变曲线

利用MATLAB,结合上节应力-应变关系式(20)，通过最小二乘法拟合，获得Mooney-Rivlin模型的关键参数：=0.882 3 MPa；=0.403 6 MPa。

3 有限元仿真分析

为了验证以上获得的Mooney-Rivlin模型的两个参数的正确性，用ABAQUS有限元仿真的方法模拟单轴压缩实验。将求得的两个参数输入到材料属性中，并定义材料属性，通过仿真求得应力-应变曲线。然后将仿真应力-应变曲线与实验所得曲线进行比较，若两者相差不大，则说明拟合获得的参数具有可靠性。

3.1 有限元建模

在ABAQUS中建立相同尺寸模型，如图6所示。

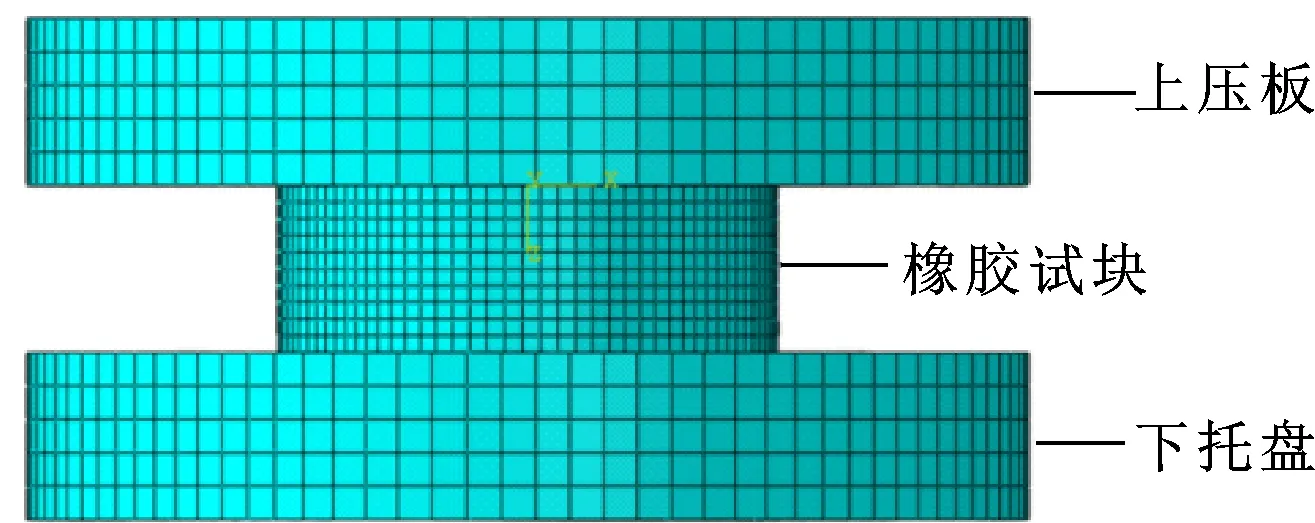
图6 ABAQUS模型

模型中材料属性如表1所示。

表 1 材料属性

根据单轴压缩实验的实际工况对模型施加边界条件，将上压板向下施加2.5 mm的位移，下托盘设置为完全固定约束,然后求解计算，在结果中查看对应的应力-应变值。

3.2 结果分析

将获得的两参数和代入上式(20)，并代入应力值，得到相应的应变值，再将应力-应变曲线与实验结果进行对比，如图7所示。可以看出：数值分析结果与实验吻合较好，仅有的偏差源于实验加载初期材料预压缩变形。对比结果验证了运用最小二乘法确定的Mooney-Rivilin 本构模型参数和的准确性。

图7 实验-数值分析曲线结果对比 图8 实验-有限元仿真曲线结果对比

将有限元仿真结果与实验数据对比，如图8所示。

通过实验测得应力-应变数据与有限元模拟数据对比，可以看到吻合度极高，最大误差为4.2%。再次验证了Mooney-Rivilin 本构模型的可靠性。

4 结论

针对防喷器胶芯用橡胶的本构模型问题，通过实验手段和仿真验证，得出以下结论：(1)基于Mooney-Rivilin 本构理论推导出的应力应变关系，可用于胶芯的仿真分析研究，模型的关键参数和可经过单轴压缩实验获得。(2)研究获得的工程应力-应变曲线是常温准静态条件下单轴压缩实验所得，适合防喷器胶芯工作实际，因此基于实验方法确定Mooney-Rivilin 本构模型参数的方法具有可靠性，可普遍用于大部分工业环境下丁腈橡胶产品的理论研究。