某型新能源减速器齿轮传动系统动力学特性

罗瑞田，郭 栋，申志朋，周 仪，陈国利

（1.重庆青山工业有限责任公司，重庆 402760；2.重庆理工大学 车辆工程学院，重庆 400054）

为应对日益严重的环境污染和燃油供应不足问题，我国制定了节能与新能源汽车的发展规划，加快汽车产业转型升级，使汽车行业朝高速化、轻量化和电动化的方向发展，使其成为汽车行业的研究热点。作为节能与新能源汽车中的重要部件，新能源减速器在工作过程中受到多种内外激励，可能导致减速器产生振动噪音，影响整车噪声、振动与声振粗糙度（Noise, Vibration and Harshness, NVH）性能。因此，研究内外激励对减速器齿轮动力学响应的影响规律，对于提升新能源汽车NVH性能至关重要。

针对齿轮传动系统的动力学特性问题，国内外学者做过许多研究，研究内容囊括了齿轮啮合刚度的精确计算、精确建模、动力学分析以及性能优化。文献[2]综合考虑时变啮合刚度以及静态传递误差对系统的影响，建立了齿轮动力学模型，并基于试验对模型进行了验证。文献[3]建立了考虑时变啮合刚度、齿轮侧隙等非线性参数的动力学模型，研究了发动机扭矩波动对齿轮副响应的影响。文献[4]基于单对齿轮啮合耦合型动力学模型，研究了齿面摩擦对系统特性的影响。文献[5]建立了具有双侧约束的单自由度非线性直齿轮动力学模型，分析了其系统的动态特性，并研究了激励幅值对齿轮冲击状态的影响。文献[6]将变速器实测激励与模型结合，通过阶次分析、频谱分析以及接触斑分析等方法定位了噪声源。文献[7]基于赫兹接触理论和分形理论，建立了减速器齿轮非线性动力学模型，研究了外界激励和系统自身参数对减速器传动系统稳定性的影响。文献[8]研究了啮合刚度以及齿轮侧隙对非对称渐开线齿轮动力学响应的影响。

本文以某型新能源减速器为研究对象，综合考虑时变啮合刚度、齿轮侧隙、静态传递误差等因素，建立减速器齿轮动力学模型，采用龙格库塔法对模型进行求解，研究扭矩波动以及啮合刚度对减速器齿轮动力学响应的影响规律。

1 减速器动力学模型

1.1 动力学模型搭建

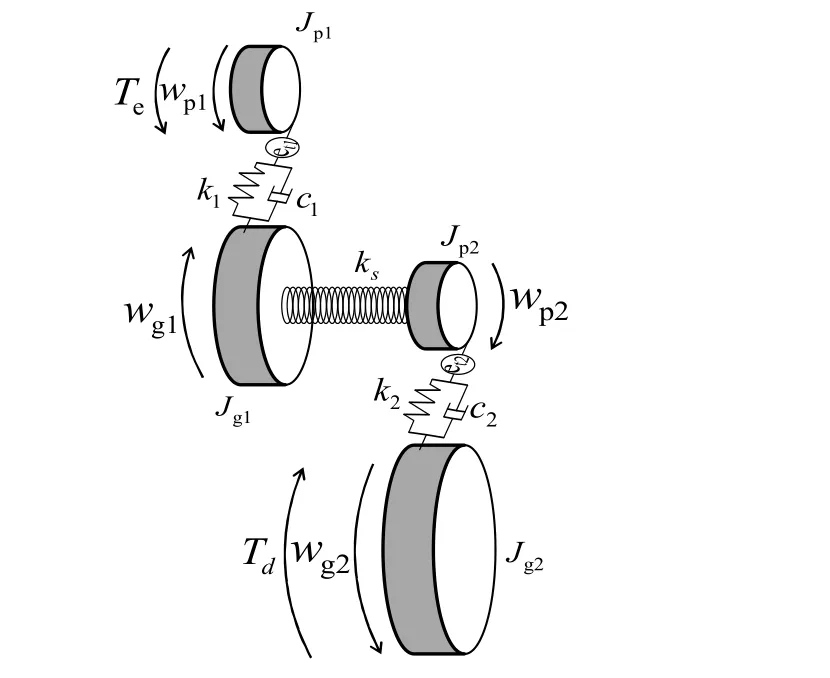
本文研究对象为某型新能源减速器，其结构如图1所示。减速器包括两对齿轮副，、分别表示一级和二级齿轮副小齿轮转动惯量；、分别表示一级和二级齿轮副大齿轮转动惯量；、分别表示一级和二级齿轮副啮合刚度；、分别表示一级和二级齿轮副啮合阻尼；、分别表示一级和二级齿轮副静态传递误差；表示中间轴扭转刚度；表示驱动力矩；表示负载力矩。减速器齿轮参数如表1所示。

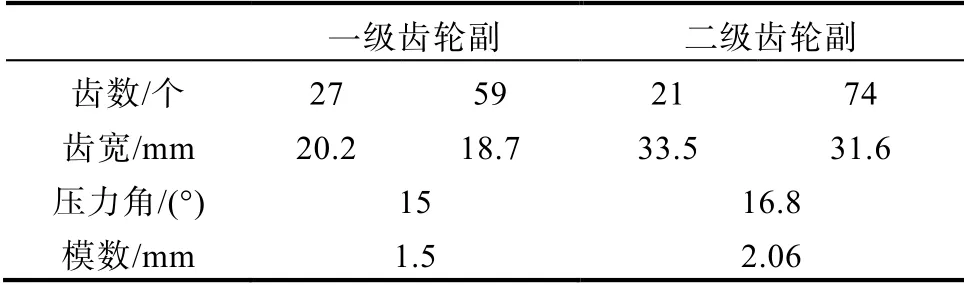
基于新能源减速器动力学模型，可得系统运动方程

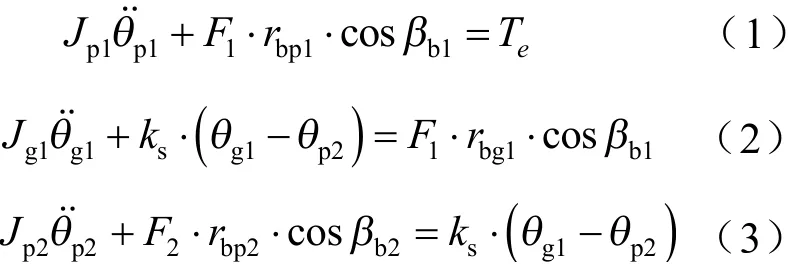
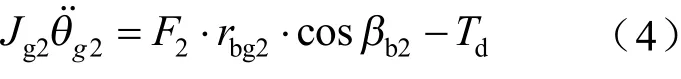
式中，、、、分别表示四个惯量的角位移；、、、分别表示四个齿轮的基圆半径；、分别表示两对齿轮副的基圆螺旋角；、分别表示两对齿轮副的啮合力。

齿轮啮合力可通过式（5）表达，式中下标（=1、2）表示齿轮副1和2，（）表示齿轮侧隙函数，表示齿轮侧隙。

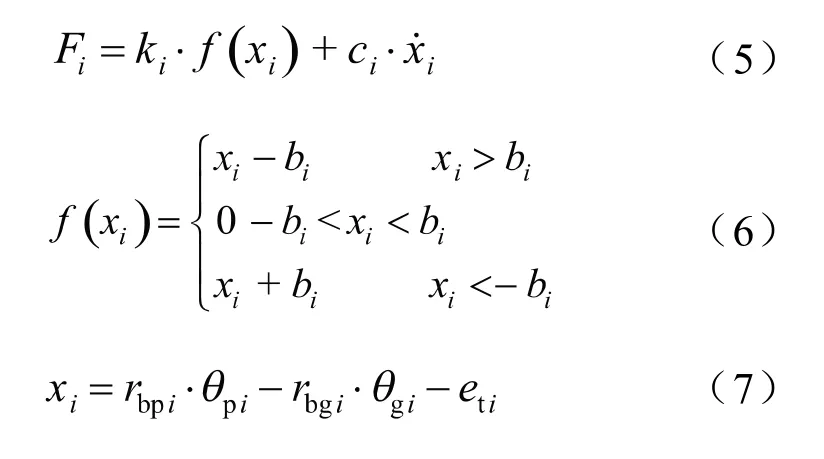
由于本文所建立的减速器齿轮动力学模型考虑了时变啮合刚度、齿隙等多个非线性参数，系统非线性程度强，因此，本文采用龙格库塔法对所建立的模型进行求解。

1.2 模型参数计算

1.2.1 时变啮合刚度

时变啮合刚度是影响齿轮动力学响应的关键因素之一，本文采用势能法计算两对齿轮副时变啮合刚度。本文研究对象均为斜齿轮，在计算斜齿轮时变啮合刚度时，通过切片法将齿轮沿着轴向均分为小薄片（如图2所示），对每片薄片运用势能法计算其时变啮合刚度，最终通过叠加的方式得到斜齿轮时变啮合刚度。势能法将齿轮啮合刚度分为接触刚度、弯曲刚度、剪切刚度、轴向压缩刚度以及基体刚度，将各部分刚度并联，得到斜齿轮副的时变啮合刚度，即为

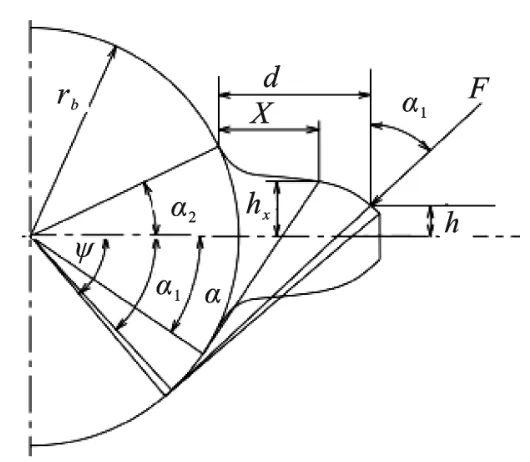
图3为通过势能法计算得到的新能源减速器两级齿轮副时变啮合刚度。

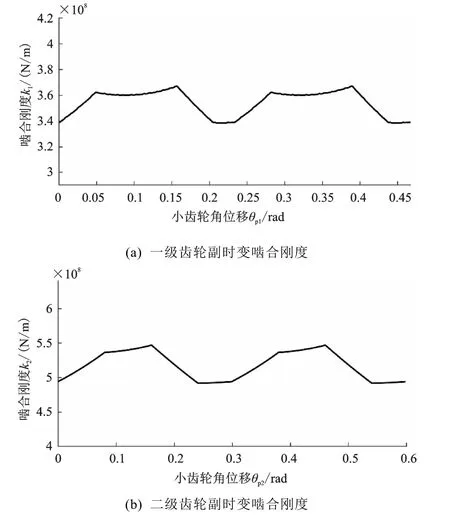
1.2.2 静态传递误差

静态传递误差的定义为当齿轮箱是完美、无误差无挠曲时，其输出轴位置与实际输出轴位置之差。齿轮静态传递误差可通过解析法和试验测得，本文采用文献[11]中的切片法计算齿轮副静态传递误差，其结果如图4所示。

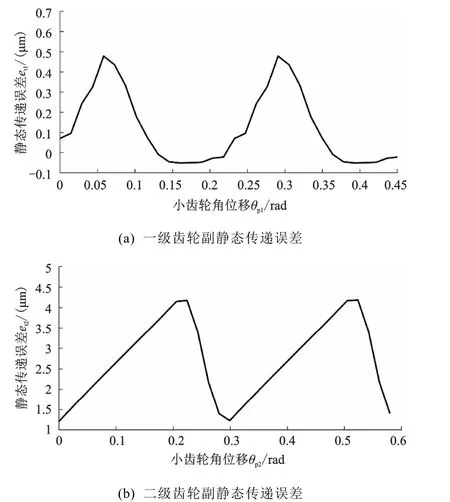
2 动力学分析

2.1 扭矩波动的影响

扭矩波动对整车传动系统NVH性能影响较大，发动机或电机扭矩波动通过传动系统传递至减速器，进而导致减速器产生振动噪声问题。本文动力学模型中的驱动力矩可通过式（9）表示，因此，计算减速器在转速1 500 r/min、平均扭矩80 Nm下，扭矩波动分别为0 Nm、100 Nm、200 Nm时系统的响应。

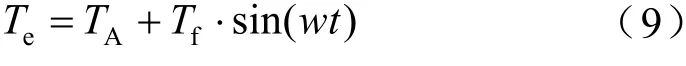
式中，表示激励角频率。

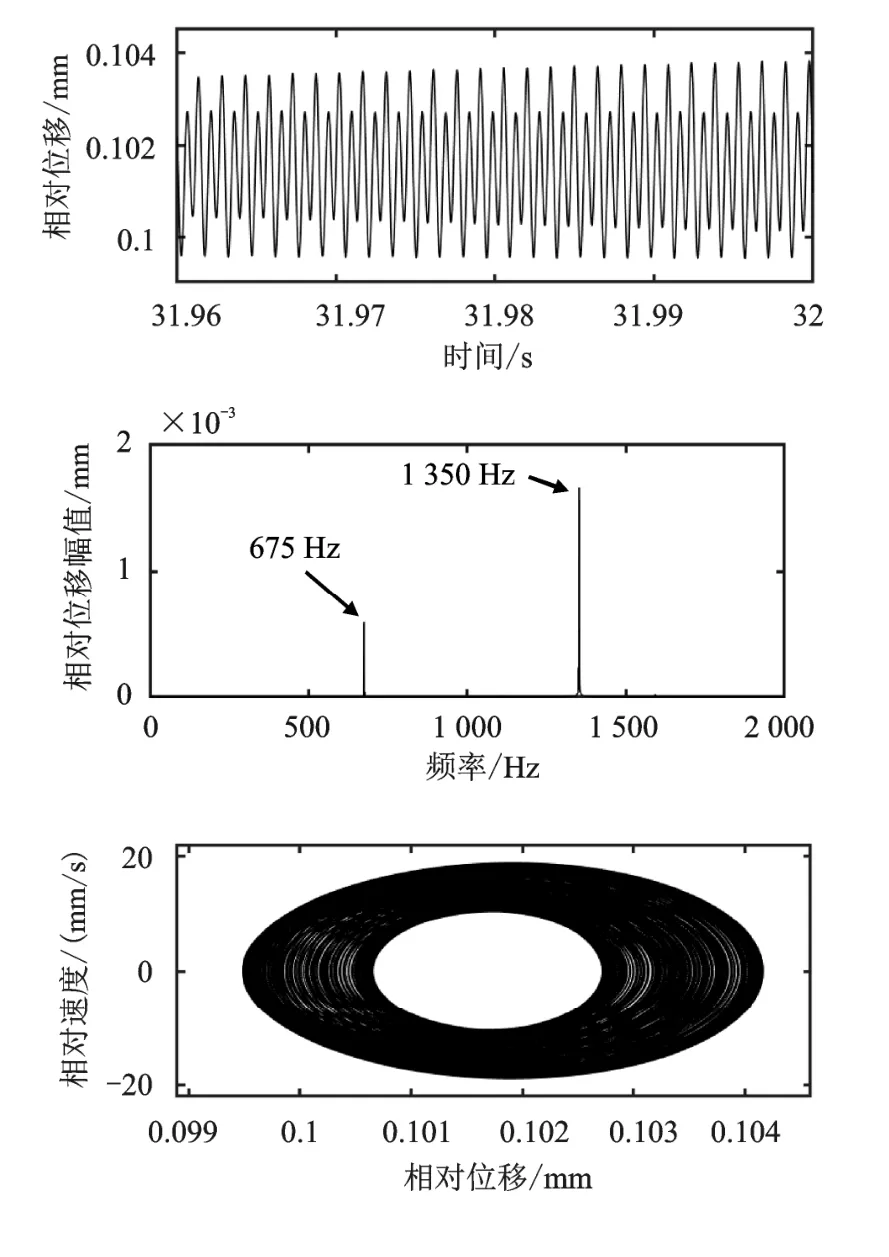
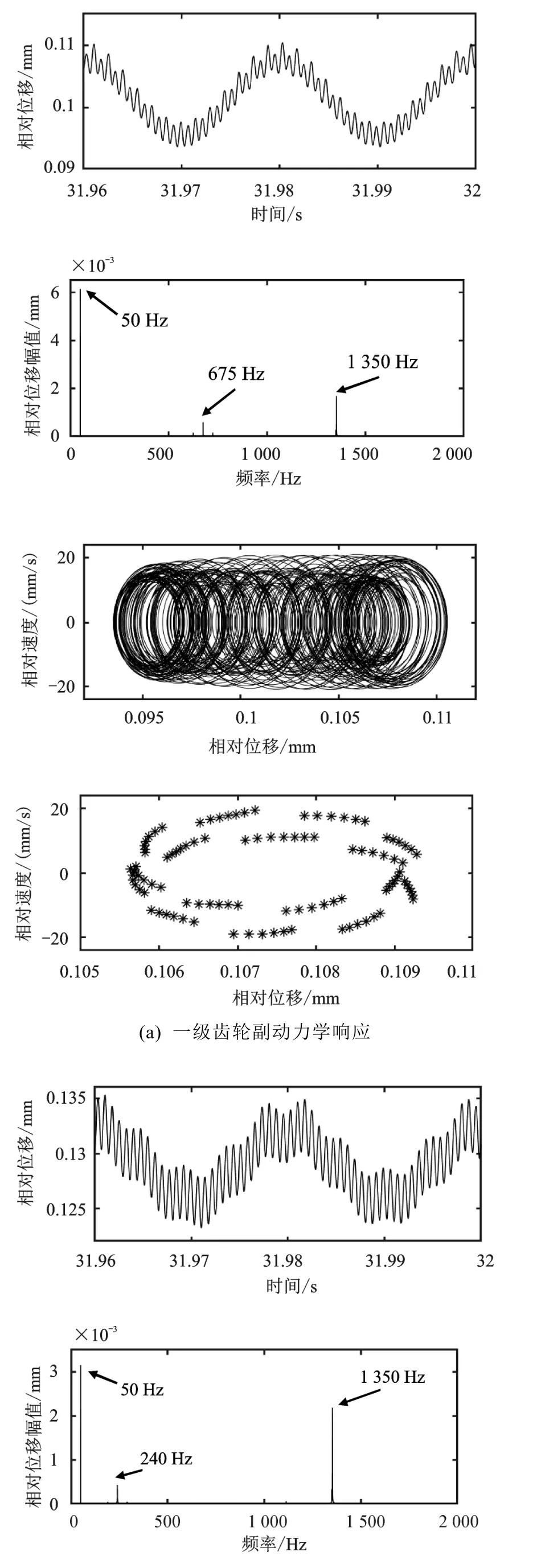
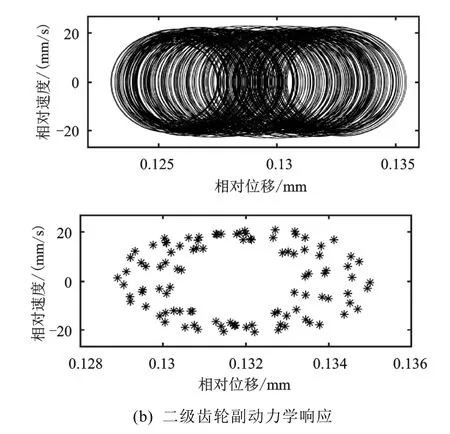
当=0 Nm时，一级齿轮副相对位移快速傅里叶变换（Fast Fourier Transform, FFT）频率成分主要为675 Hz以及1 350 Hz，其中675 Hz为啮合频率（1 500×27/60），1 350 Hz为2阶啮合频率，如图5(a)所示；二级齿轮副FFT频率成分主要为240 Hz以及1 350 Hz，240 Hz为二级齿轮啮合频率（1 500×27×21/（60×59）），如图5(b)所示。通过图5(a)(b)中的相图以及庞加莱映射图可看出，两对齿轮副均作概周期运动。当=100 Nm时，齿轮相对位移曲线趋向于正弦形式，一级齿轮副相对位移FFT频率成分主要为50 Hz、675 Hz以及1 350 Hz为激励频率，如图6(a)所示；二级齿轮副FFT频率成分主要为50 Hz、240 Hz以及1 350 Hz。尽管图6中的相图以及庞加莱映射图反映出此时两对齿轮仍做概周期运动，但是通过FFT图可看出，扭矩波动增大，相对位移幅值增加。当=200 Nm时，齿轮相对位移曲线更趋向于正弦形式，两级齿轮副相对位移FFT频率成分主要为激励频率。此时两对齿轮副做概周期运动，通过FFT图可看出，扭矩波动增加到200 Nm后，相对位移幅值进一步增加。

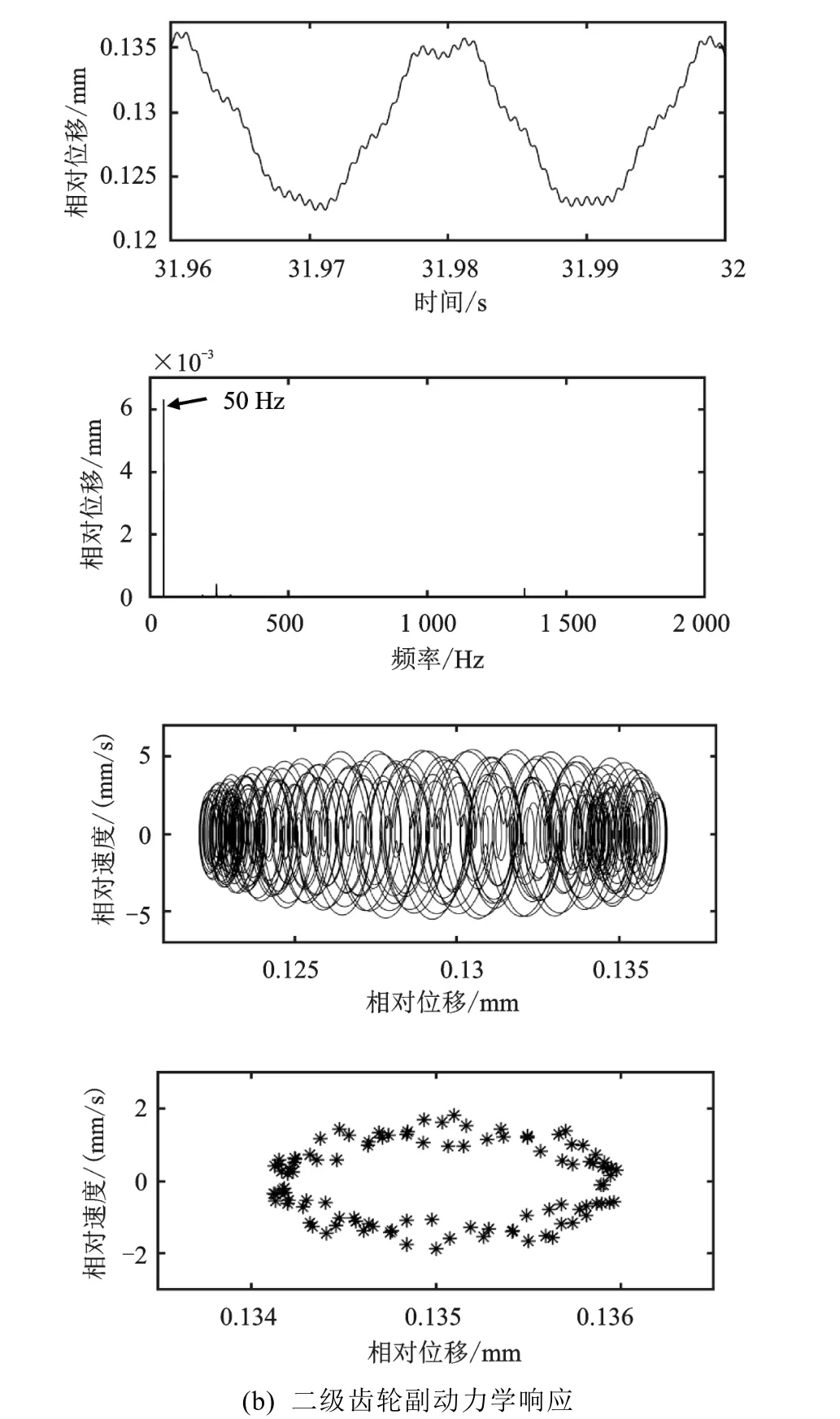
2.2 啮合刚度的影响

为了将1.2.1中计算得到的齿轮啮合刚度引入到模型中，对啮合刚度进行傅里叶展开，转换为式（10）的形式。本节将探究平均啮合刚度对减速器齿轮动力学性能的影响。因此，计算减速器在转速1 500 r/min、平均扭矩80 Nm、扭矩波动0 Nm下，平均啮合刚度分别为0.5×、1×、2×时系统的响应。

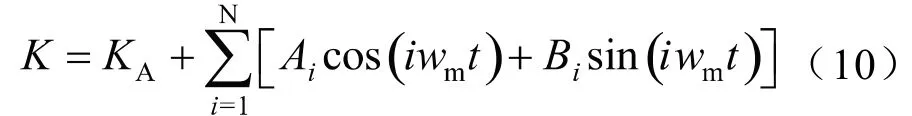
式中，表示啮合角频率。

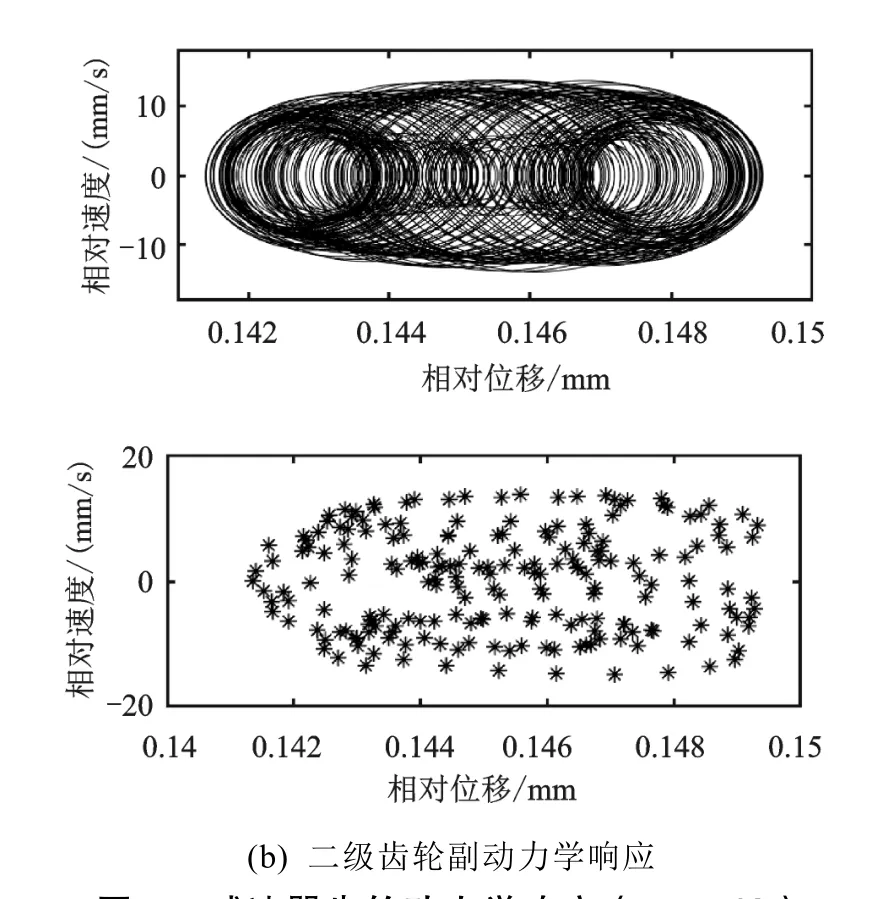
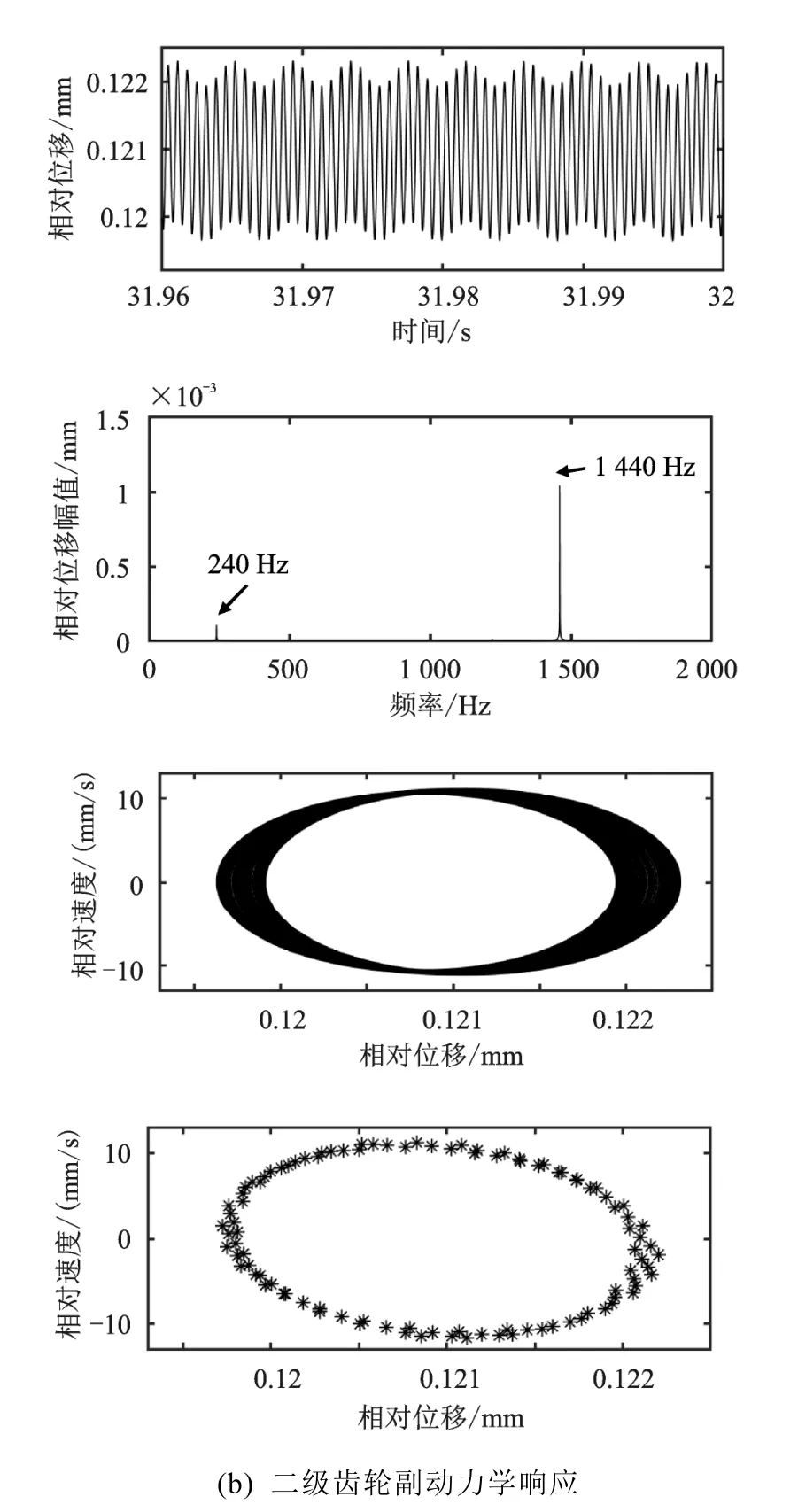
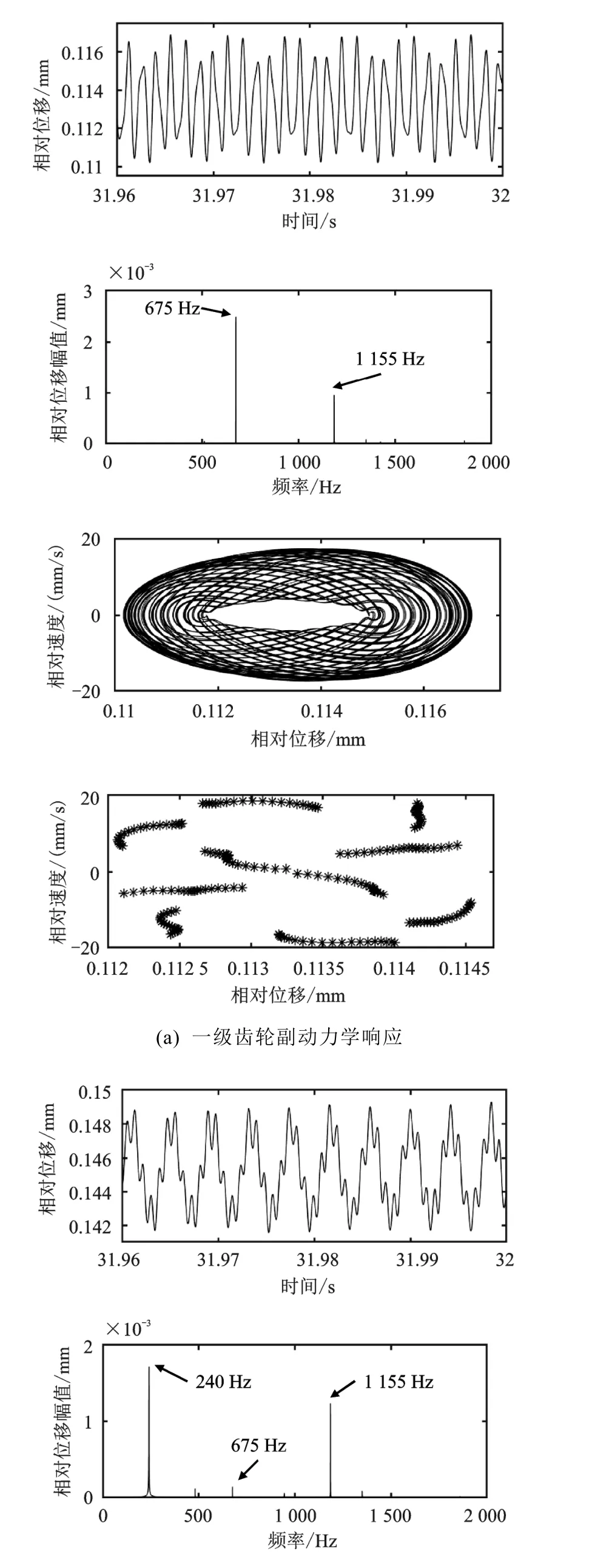
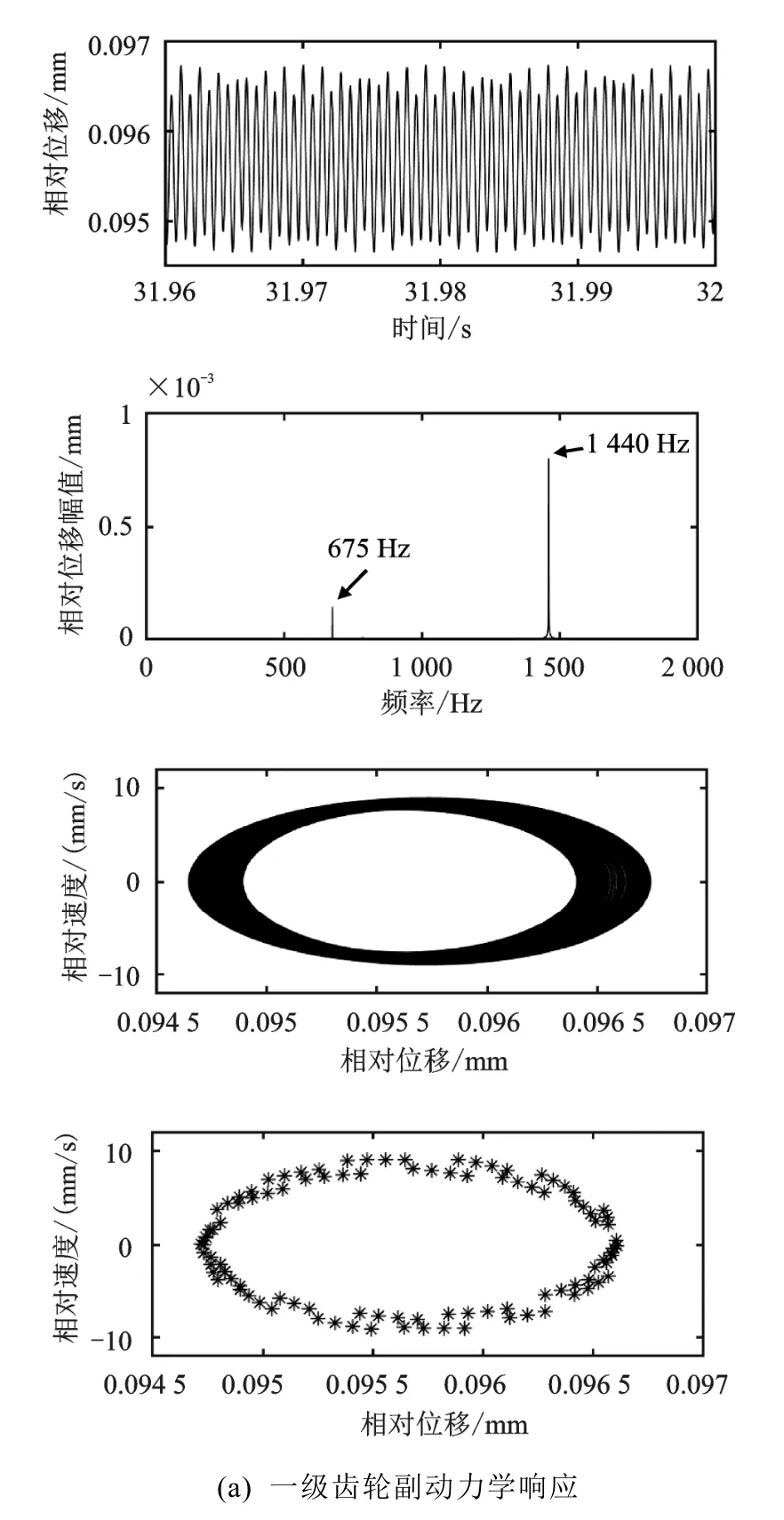
当平均啮合刚度为0.5×时，如图8(a)(b)所示，一级齿轮副相对位移FFT频率成分主要为675 Hz以及1 155 Hz；二级齿轮副FFT频率成分主要为240 Hz、675 Hz以及1 155 Hz。通过相图以及庞加莱映射图可看出，在较低的平均啮合刚度情况下，两对齿轮副作混沌运动。当平均啮合刚度为1×时，结果如图5(a)(b)所示，一级齿轮副相对位移FFT频率成分主要为675 Hz以及1 350 Hz，二级齿轮副FFT频率成分主要为240 Hz以及1 350 Hz。通过图5(a)(b)中的相图以及庞加莱映射图可看出，两对齿轮副做概周期运动。当平均啮合刚度为2×KA时，结果如图9(a)(b)所示，一级齿轮副相对位移FFT频率成分主要为675 Hz以及1 440 Hz，二级齿轮副FFT频率成分主要为240 Hz以及1 440 Hz。通过相应的相图以及庞加莱映射图可看出，两对齿轮副做概周期运动。对比平均啮合刚度较小时，减速器齿轮副动力学响应情况，增大齿轮副平均啮合刚度，齿轮相对位移FFT幅值减小，齿轮副从混沌状态转变为概周期运动状态。

3 结论

本文考虑了齿轮时变啮合刚度、侧隙以及静态传递误差等非线性因素，建立了某型新能源减速器齿轮动力学模型，并通过4/5阶龙格库塔法对模型进行求解。通过计算分析不同条件下减速器齿轮动力学响应情况，得出结论：（1）输入扭矩波动对齿轮动力学影响较大，增大扭矩波动会使齿轮相对位移波动幅值增加，齿轮副相对位移曲线趋向于正弦形式，激励频率对应成分对齿轮动力学响应的影响最大；（2）增大齿轮平均啮合刚度，齿轮相对位移波动幅值降低，系统从混沌运动变为概周期运动。