电缆连接套结构静力学分析及优化

陈 果，王仓平，任宏东

（中国核工业二三建设有限公司，北京 100000）

0 引言

电缆线敷设常常涉及通信设施等工程领域，传统缆线敷设过程主要以人工为主，人工敷设存在人员需求大、敷设效率低、敷设过程不安全等缺点。尽管当前大截面电缆敷设时有卷扬机和电缆输送机作为电缆敷设的辅助工具，电缆敷设效率和安全性有所提高，但是采用卷扬机和输送机进行电缆敷设效率依旧较低。因此，缆线敷设机器人以相对安全可靠的优势发展起来［1-2］。电缆敷设机器人使用自动控制技术，融入当前科技技术，通过机械手对电缆抓附，机器人拖动电缆在电缆桥架内行走，电缆到达指定位置后放置在电缆桥架内。电缆敷设机器人主要由全向轮移动底盘、伺服牵引装置、支臂调节装置、锚定固定装置、运动控制单元、系统检测单元、导航避障单元、电源充电单元等功能模块组成，上述整套方案可实现电缆的自动化敷设牵引作业。采用电缆敷设机器人敷设缆线时较人工缆线敷设效率会提高10倍以上，同时具有人工投入少、敷设过程可控等优点。电缆连接套结构作为缆线机器人连接缆线的关键结构，主要作用在于连接电缆线和缆线敷设机器人，由此可见保证电缆连接套结构的安全可靠关系着缆线敷设能否快速高效地进行。

销轴在某些工装中起到关键作用，采用有限元方法对其进行应力应变或模态分析，最终获得的仿真结果已成为指导设计的主要依据［3-4］。文献［5］考虑盘式制动器在频繁制动过程中容易引起销轴断裂，利用有限元方法对销轴进行受力分析，为盘式制动器的设计提供帮助。常见引起销轴断裂的原因是疲劳，这与材料本身属性息息相关。因此在设计时需要充分考虑材料属性以及实际使用工况等多个因素。防止销轴断裂的方法有改善焊接工艺技术和改变销轴材料等［6］。李杰等［7］对油缸用35#钢销轴断裂的原因进行了物理检测及有限元分析，发现销轴的加工裂痕以及热处理容易形成裂纹源从而导致存在销轴断裂隐患。近年来随着计算机以及有限元理论的发展，有限元仿真分析已成为工程设计必不可少的工具之一，ANSYS Workbench集成了结构、流体、电磁等多学科仿真计算模块，其中结构分析中的静力学已经被广泛应用于工程设计领域。静力学分析的主要步骤包括：将工程实际问题简化为分析用的物理模型、定义材料属性、网格划分、载荷约束加载并给出方程求解的边界条件、求解计算、模型优化，结果后处理及分析。

本论述通过ANSYS Workbench静力学分析模块对电缆连接套结构进行分析，分析其位移变形及等效应力；着重分析其关键受力部件即销轴的应力分布，并对销轴尺寸及材料进行优化，为电缆连接套结构的设计提供依据。

1 静力学基本理论及模型建立

1.1 静力学基本理论

结构静力学分析在Ansys workbench的Static Structural中进行，不考虑与时间相关的物理量，忽略惯性力和阻尼的情况下，静力学分析的有限元方程可写成：

式（1）中：[ K ]为刚度矩阵，{ x} 为位移矢量，{F } 为载荷矢量。若[ K ]为定值，此时材料结构变形小且为线弹性，求解的是线性静力问题，反之为非线性静力问题。为求解上述有限元方程，在进行实际工程问题分析时，需要考虑几何模型的尺寸、材料属性、约束条件以及所施加的载荷。

工程零件在外部载荷较大的情况下容易发生结构失效，包括零件的变形、断裂、磨损、弹性、塑性、断裂韧性等。为避免上述结构失效，在零件设计时必须综合考虑各个性能，常采用应力分析的方法预测结构应力应变和位移。等效应力是指将三个主应力表示为一个等效的正值应力，其定义为：

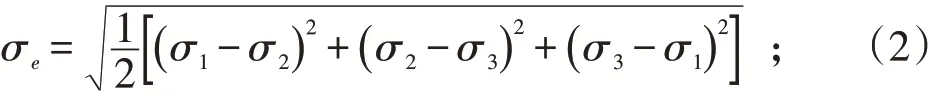
其中：σ1、σ2、σ3分别为第一主应力（Maximum Principal）、第二主应力（Maximum Principal）和第三主应力（Minimum Principal），同时 σ1>σ2>σ3。等效应力σe（Equivalent von-Mises）常常在形状改变比能原则中预测材料的屈服强度，而位移和应变则描述材料的变形状态。

强度设计准则作为设计主要依据至关重要，其主要包括断裂准则、屈服准则和莫尔准则，其中断裂准则主要包括最大拉应力准则和线性断裂力学准则。屈服准则作为强度设计准则的一种主要包括最大剪应力准则和形状改变比能准则。本论述主要使用形状改变比能准则，它是指当一种材料处于任何应力状态时，只要形状改变比能达到极限值，材料就会发生屈服破坏。失效判据为σe=σs，设计准则为σe≤[ σ] 。莫尔准则主要适用于拉压强度不相等的材料，比如铸铁等脆性材料。

1.2 三维有限元模型

电缆敷设机器人的重要问题之一是电缆与机器人的连接问题，安全可靠的连接关系可以保证缆线机器人正常工作，同时提高缆线敷设效率。如图1所示为电缆机器人的电缆连接套结构，左边的钢丝绳连接端与机器人内部的钢丝绳相连接，缆线固定端与钢丝绳连接端通过螺纹连接，右侧的缆线被嵌套在其上面的钢丝绳网套上，可以实现向左拉动，缆线与钢丝绳之间的摩擦力足够拉动整个缆线水平向左移动。钢丝网套通过套箍拧成一个钢丝套环套在销轴上，外侧的涨紧套起涨紧与保护作用。

图1 电缆连接套结构

为了验证缆线敷设机器人工作时电缆连接套结构的可靠性，对电缆连接套结构进行静力学仿真分析，同时研究当拉力不同时，不同材料的销轴是否满足应力应变要求。如图2所示，显示了电缆连接套结构的三维简化模型，坐标原点位于左侧钢丝绳连接端的侧表面，模型总长312 mm，其中销轴为关键受力部位，图2中销轴的半径为7 mm，高为36 mm。需要说明的是，缆线机器人最大牵引力为15 000 N，正常工作时其牵引力小于15 000 N，因此在牵引力分别为15 000 N、12 000 N、9 000 N 时，查看销轴的静力学性能，分析其形变与屈服强度是否满足设计要求，同时查看电缆连接套结构的位移与形变。

图2 电缆连接套结构的三位简化模型

各部件的材料参数见表1所列，有限元仿真用到的主要物性参数有密度、杨氏模量、泊松比及屈服强度等。

表1 材料特性参数

2 网格划分及添加载荷

根据上述分析，在三维建模软件中画出电缆连接套，导入Ansys workbench的静力学分析模块进行材料、网格、载荷及求解的相关设置。网格结构如图3所示，网格划分采用Ansys workbench 自带的mesh 模块进行划分，对于上述电缆连接结构，四面体网格足以满足计算要求，销轴及钢丝绳等部件进行局部加密处理，同时不同部件之间的网格节点相互对应，以保证仿真数据通过网格节点传递的准确性，网格节点数目为14万左右。网格满足有限元静力学计算要求。

图3 电缆连接套结构有限元网格划分

有限元模型约束条件及假设：为分析电缆连接套静力学性能，不考虑其随时间的变化状况。如图2 所示，电缆连接套左侧孔内施加向左的牵引力分别为15 000 N、12 000 N、9 000 N；电缆连接套左侧实际为缆线固定端，假设其为固定约束，在牵引力的作用下达到动态平衡。在现有材料的基础上查看电缆连接套结构各个部位的位移与抗屈服性能。分析研究时忽略各个材料的不均匀性。

3 仿真结果分析

对电缆连接套结构进行静力学分析，如图4 所示，为牵引力为15 000 N时，电缆连接套的位移分布，从图中可以看出，最大位移为0.1139 mm时最大变形发生在左侧孔受力区域，最小变形发生在右侧固定端。进一步分析，当牵引力为12 000 N 和9 000 N 时，电缆连接套结构的最大位移为0.091 mm 和0.068 mm，可见随着牵引力地减小，最大变形也在减小，且最大变形发生的位置不变。综上所述，牵引力在合理范围内时电缆连接套结构的位移形变均不超过0.2 mm，故其位移形变可以忽略。

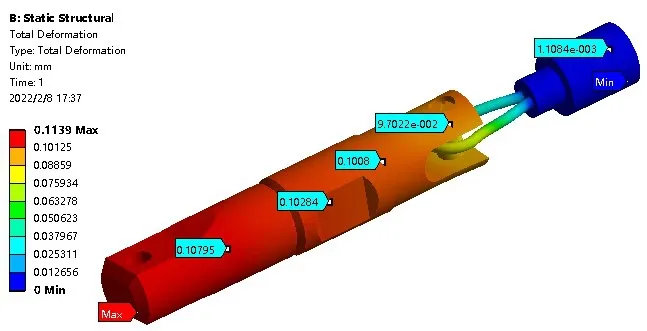
图4 牵引力为15000N时，电缆连接套的位移分布

电缆连接套结构的静力学分析中，销轴与钢丝网套接触的部分会产生很大的局部接触应力，所以销轴处最容易出现应力集中。为了验证关键受力部位销轴的应力分布，如图5所示，为不同牵引力对应销轴的等效应力分布，销轴材料为45#钢。由图5 可以看出：随着牵引力F地增大，其最大等效应力也在逐渐增大，最大等效应力分布在销轴中部，牵引力F等于9 000 N时，最大等效应力为299.14 MPa，未超过材料的屈服强度；牵引力F 等于12 000、15 000 时，销轴的最大等效应力分别为399 MPa和499 MPa，此时应力最大值超过了材料的屈服强度355 MPa，故不满足设计要求。

图5 不同牵引力对应销轴的等效应力分布

对于上述不足，现提出两种解决方案：第一种方案——不改变销轴材料属性的前提下，加大销轴半径；第二种方案——改变销轴的材料属性，保持其半径不变。如图6 所示，销轴半径改变后其最大等效应力分布，可以发现，随着销轴半径地增大，销轴的最大等效应力在逐渐减小，当销轴半径增大至10 mm时，销轴的最大等效应力为384.25 MPa，其最大等效应力仍然大于销轴材料的屈服强度355 MPa，如果再增大销轴半径，直径为42 mm的缆线固定端与销轴不能良好配合，由此考虑第二种方案，即改变销轴材料。材料的机械性能决定材料的使用工况，选取销轴材料时往往会考虑材料的弹性、强度、刚度、硬度、疲劳强度等特性。一种材料对应的应力增长是有限的，超过限度后材料就会被破坏。就销轴材料45#钢而言，其作为最常见的一种优质碳素钢可以作为大部分机械零部件的材料，但是它的硬度不高，屈服强度为355 MPa，若要用于硬度较高或磨损严重的零部件时需要慎重考虑。对于电缆连接套结构中的销轴而言，最大拉力为15 000 N 时，45#钢已经不能满足形状改变比能准则，因此需选用高强度、高硬度的材料。20 CrNiMo 钢及40 CrNiMo 钢两种材料属于高淬透性合金钢，其强度高塑性好，通常情况下被用于高强度的关键受力部位。销轴可选新材料的物性参数见表2所列。

图6 销轴半径改变后其最大等效应力分布

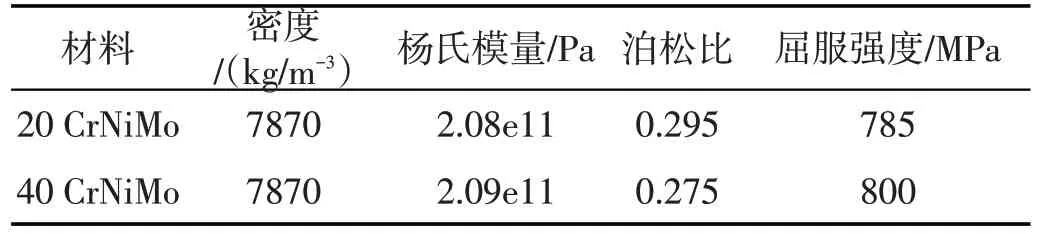
表2 销轴新材料属性

如图7 所示，当销轴材料为20 CrNiMo 和40 CrNi-Mo、F=15 000 N 时销轴的等效应力分布。可以发现材料为20 CrNiMo时，等效应力的最小值在销轴上下两侧，最大值在销轴中部，销轴的最大等效应力为495.91 MPa；材料为40 CrNiMo 时，等效应力最大值与最小值的分布位置不变，销轴的最大等效应力为498.09 MPa。根据形状改变比能准则，两种材料对应销轴的等效应力的最大值均不超过材料的屈服强度，满足缆线敷设机器人最大牵引力的设计要求。故第二种方案较为合理，销轴可更换上述两种屈服强度较高的合金钢材料。

4 结论

本论述对电缆连接套结构进行静力学仿真分析，分析其位移及等效应力分布，对销轴的等效应力进行重点分析，得到以下结论：牵引力在合理范围内时电缆连接套结构的位移形变均不超过0.2 mm，故此时其位移形变可以忽略；当牵引力为最大F=15 000 N、销轴材料为45#钢时，销轴应力最大值超过其屈服强度，增大销轴半径虽然可以减小应力，但仍不能满足设计要求。因此考虑更换销轴材料且保持原有半径大小的方案，经过验证可选20 CrNiMo 或40 CrNiMo 作为销轴的新材料，半径保持7 mm 不变，此时销轴应力满足小于屈服强度的设计要求。