考虑航线网络重叠航段的双寡头竞争市场集装箱班轮运输动态定价模型

宋 巍 杨华龙 郑建风

(大连海事大学 交通运输工程学院,辽宁 大连 116026)

0 引言

集装箱班轮运输是国际工业品海运贸易的主要运输方式,其具有“定线、定船、定期和定港”等特征[1],即船公司在既定的航线上,选取一组特定型号的船舶,按照规定的船期表,顺序挂靠多个选定的港口,为客户提供规则的班轮运输服务。为了降低运营成本,提高市场占有率及航运竞争力,船公司之间纷纷加强合作并组建海运班轮联盟,集装箱班轮运输市场由此呈现出寡头竞争的市场格局[2],如近期相继组建的2M(马士基航运和地中海航运联盟)、Ocean(法国达飞轮船、台湾长荣海运、香港东方海外及中国远洋海运集团联盟)、THE(赫伯罗特、阳明海运、日本邮船、川崎汽船、商船三井、韩进海运联盟)三大海运联盟。因而,在某些航线上,相继出现了两家(或多家)寡头船公司提供无差异的班轮运输服务,此时运价便成为寡头船公司间竞争的关键[3]。此外,由于集装箱班轮运输市场总体上呈现运力供求失衡,衰退期延长等特征,因此,如何制订合理的集装箱班轮运价,已成为寡头竞争市场环境下船公司的核心决策问题。

班轮运输定价一直是学者们研究的热点问题。运输需求是船公司定价决策时所关注的最主要因素之一,结合运输需求对运价的影响,Lim等[4]考虑季节性需求波动,构建了托运人与承运人的竞价模型。Garrido[5]针对班轮运输的弹性需求情形,运用复式拍卖方式确定班轮运价。在此基础上,Qu等[6]则进一步分析了港口补贴政策对干线/支线承运人和托运人的影响,建立了干线/支线班轮运输定价模型。此外,考虑集装箱班轮运输市场面临的产能过剩以及市场竞争等因素,Zhou和Lee[7]结合空箱调运成本,运用伯川德纳什均衡原理,研究了双寡头市场竞争环境下的班轮运输定价问题。Chen等[8]将运输物品分为高价值和低价值两类,利用运输低价值货物来平衡市场的需求不平衡问题,构建了双寡头市场竞争环境下的集装箱班轮运输定价模型。考虑集装箱班轮运输公司对风险规避的影响,Zheng等[9]研究了两家容量规模不同的船公司的集装箱班轮运输定价策略,提出博弈竞争定价决策模型。Choi等[10]分析风险态度和需求波动对两个集装箱船公司之间服务定价博弈的影响,建立竞争下对风险敏感的集装箱运输公司的定价均衡。

上述文献从需求因素扩展到市场竞争、货物分类和风险规避等因素,对班轮运价问题进行了较为深入的研究,取得了许多有益的研究进展,但这些研究都是基于既定或预设的运输需求波动状态而得出的静态定价结果,在面对变化多端的班轮运输市场环境时,其适用性较为有限。为此,一些学者借鉴收益管理理论方法在航空运输领域中的成功应用经验,又进一步结合班轮运输的特点,开展了班轮运输动态定价方面的研究。如,Lee等[11]应用启发式算法解决班轮运输中出现的延迟收益管理问题,制定混合整数线性规划模型,确定海运能力最优分配的阈值政策。李冰州[12]结合集装箱船舶体积和重量的二维运力约束,研究了班轮运输二维多航段多箱型在线动态定价模型;杨华龙等[13]在将托运人细分为合同客户和普通客户的基础上,构建了两阶段舱位分配模型以及现货市场分时段的班轮运输动态定价模型;汪挺松和李曼[14]引入奖惩因子,构建了考虑时间敏感货物对配送时间要求的班轮运输两阶段舱位分配和现货市场动态定价模型。考虑到两家船公司在单一起讫港口对(OD流)上的竞争关系,Yin等[15]结合托运人的偏好因素,应用效用函数理论,建立了单OD流集装箱班轮运输动态定价模型,初步解决了市场竞争环境下单OD流的班轮运输动态定价问题。

以上研究虽然取得了一些可喜的研究成果,但与航空运输领域研究成果的广泛应用相比,班轮运输动态定价的研究与应用仍很匮乏[16]。主要是由于班轮运输船舶挂靠港口和货物OD流众多,航线网络结构复杂且存在航段重叠,现有研究大都仅考虑单航线或单OD流的情形,与联盟下班轮运输的实际尚存在一定的差距。鉴于此,本文在现有研究的基础上,综合考虑客户运价敏感度和市场竞争强度等因素对集装箱运输需求及运价的影响,从以下两方面进行创新性的扩展研究:一是依据班轮运输多港挂靠和客户分类的特征,将单OD流扩展至多OD流,提出客户分类条件下考虑多OD流的班轮运输即期市场动态定价策略;二是结合班轮联盟形成的双寡头竞争市场环境,将单航线班轮运输问题扩展至网络多航线问题,提出考虑重叠航段的双寡头船公司班轮运输分时段动态定价策略。以期为实际双寡头竞争市场环境下船公司班轮运营管理提供科学的决策依据。

1 问题描述

在集装箱班轮运输的相同(或相近)远洋区域内,通常会有不同联盟旗下的两家(或多家)寡头船公司经营同一航线,提供无差异的集装箱班轮运输服务,船公司之间互为竞争对手。如在远东—美西的跨太平区域,Ocean联盟旗下的中远海运(China Cosco shipping corporation limited)和THE联盟旗下的阳明海运(Yang Ming marine transport corp)都经营AAC航线,提供无差异的集装箱班轮运输服务,两家船公司呈现双寡头竞争的情形。而且,两家船公司在跨太平区域的集装箱班轮运输网络中经营多条与AAC航线存在航段重叠的航线,如表1所示。

表1 两家船公司经营与AAC存在航段重叠的航线Table 1 Two shipping companies operate routes that overlap with AAC

由表1可以看出,Ocean联盟旗下的中远海运和THE联盟旗下的阳明海运两家寡头船公司在AAC航线上的班轮挂靠港口及顺序完全相同,两家公司在该航线上互为直接竞争对手。且中远海运的AAC航线与CEN航线,都包含上海—长滩港口对的重叠航段,AAC航线与AAC4航线,都包含上海—长滩港口对和宁波—长滩港口对的重叠航段;阳明海运的AAC航线与PN31航线和PN32航线,都包含上海—西雅图港口对和宁波—西雅图港口对的重叠航段。

船公司面临的客户大体上可分为两类:一类是长期合同客户(一般为大客户),这类客户通常会提前几个月或者一年签订运输服务合同,具有运价相对固定的特点[17];另一类是即期市场客户,即期市场客户一般在船期临近时开始订舱,运价容易出现较大波动[18]。在考虑客户分类的基础上,集装箱班轮运价决策的重点主要是对即期市场客户的动态定价。进一步地,由于集装箱班轮运输具有适用于收益管理理论的典型特征[19],因此,船公司需要综合考虑客户分类特征和时间因素,并结合即期市场客户需求的变动规律和竞争对手的定价策略,对即期市场客户进行动态定价决策,以实现船公司收益最大化的目标。

在即期市场上,集装箱货运需求与运价呈负相关关系[7],即运价越高,则需求越低。同时,集装箱货运需求的运价敏感性又随着订舱(揽货)截止期的临近而减弱[9],即越临近订舱截止期,货运需求对运价变化越不敏感。为此,船公司可将揽货期划分为若干个时段,在每个不同的时段采取不同的定价(即分时段动态定价),以使班轮运输收益最大。其中,t表示揽货期的某个时段,t值越小表示越接近订舱截止期,如图1所示。

图1 即期市场揽货期时段划分Figure 1 Division of booking horizon in spot market

此外,由于不同航线相同OD流间的集装箱运价应保持一致,故在重叠航段上,客户主要根据航线上船舶的挂靠港口顺序、航行时间和到离港日期等选择集装箱货物运输航线。因此,班轮定价不会影响客户货物运输量在各条航线重叠航段之间的分配比例。

根据以上问题描述,为了便于建模求解,本文做以下假设:

(1)决策期内船舶挂靠的港口及其顺序已知;

(2)决策期内OD流间长期合同客户的货运需求量已知;

(3)即期市场客户的运价敏感度与揽货期及运输需求量相关[9];

(4)即期市场潜在客户是理性的,不存在个人偏好,且对于运输时间和运价都具有一定的敏感性[20];

(5)决策期内船公司在各条航线重叠航段之间的客户货物运输量分配比例已知。

2 建模与求解

2.1 参数与变量定义

本文的参数符号说明如下:

N表示船舶挂靠港口的个数;

I={1,2,…N}表示船舶挂靠港口的集合,船舶挂靠港口的顺序为1→2→…→N→1,船舶挂靠相邻两个港口之间的航线部分称作航段,船舶由港口i出发的航段亦记为航段i,i∈I。

s表示货物运输的OD流(起讫港口对);

S表示所有货物运输的OD流集合,s∈S;

T表示船公司在即期市场按时段(周)划分的揽货周期;

t表示揽货周期T内的某个时段(周);

a表示船公司,a=1,2;

Ca表示船公司a的船舶容量;

表示船公司a在OD流s上的合同客户需求;

δsi=1表示OD流s的货物运输经过航段i,δsi=0表示OD流s的货物运输不经过航段i;

表示船公司a在OD流s(s与其他航线的航段重叠)上的客户货物运输量分配比例系数;

表示t时段船公司a在OD流s上的潜在的即期市场集装箱需求;

表示船公司a在OD流s上的单位集装箱运输成本,包括装港拖箱费、码头操作费、运费、卸港码头操作费、拖箱费等费用[21];

表示在t时段OD流s上客户需求对船公司a运价的敏感度;

表示船公司a在OD流s上的市场竞争强度,即每降低一个单位运价从竞争对手吸引过来的需求;

Rs表示OD流s的一个运价上限;

表示船公司a在OD流s上长期客户的集装箱运价;

本文的变量定义如下:

表示t时段船公司a在OD流s上即期市场客户的集装箱运价。

表示t时段船公司a在OD流s上的集装箱运输需求量,是关于集装箱运价的因变量。

2.2 模型构建

在双寡头竞争市场环境下,两家船公司提供无差异的集装箱班轮运输服务,分别以自身利润最大化为决策目标,各自独立定价。假设船公司a的即期市场的班轮运输需求与其自身运价及竞争对手运价线性相关[7-9],需求函数中所有参数都是确定的,且对于两家船公司都是已知信息,则t时段在OD流s上客户班轮运输需求量与船公司a运价之间的函数关系如下:

这意味着对于船公司a而言,其在t时段OD流s上运价每降低一个单位,其客户班轮运输需求量将增加个单位,其中是需求对运价的敏感系数,即运价降低触发的需求增加系数;是市场竞争强度系数,即船公司运价降低从竞争对手吸引过来的需求增加系数;是航线网路各OD流(航段)客户货物运输量分配比例系数,由于船公司在航线网路重叠航段(相同OD流)的定价相同,因此,客户货物运输量在各条航线重叠航段之间的分配比例也不会改变。于是,船公司a以收益最大化为目标的即期市场分时段动态定价模型M为:

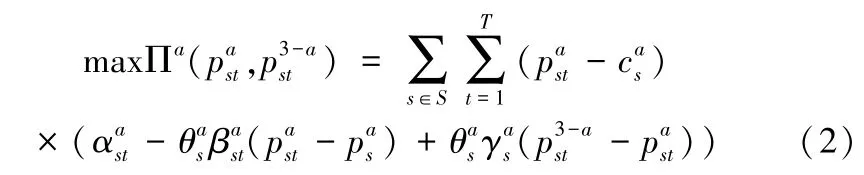
约束条件为:

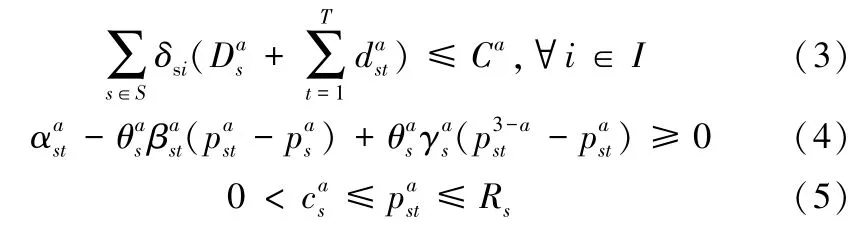
目标函数式(2)表示船公司a即期市场的收益;约束式(3)表示船公司a在每个航段i上的所有集装箱舱位需求量小于船舶容量;约束式(4)表示船公司即期市场的班轮运输需求为非负;约束式(5)为船公司a在OD流s上的集装箱运价不能高于其价格上限Rs,利润不能低于成本。

定理1模型M是关于船公司a集装箱运价策略集pa=的凸规划问题。

目标函数Πa关于的一阶导数为:

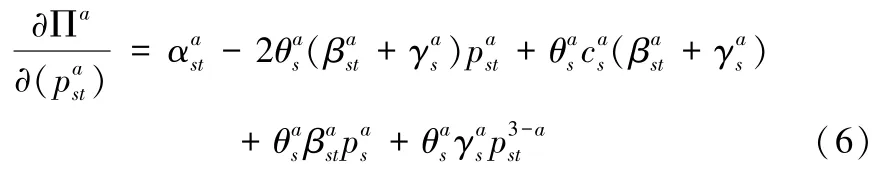
二阶导数为:

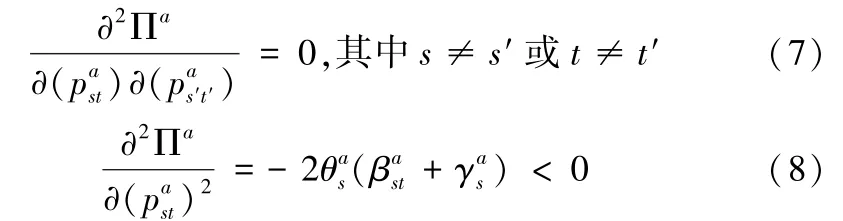
因此,船公司a目标函数函数Πa的海塞(Hessian)矩阵为:

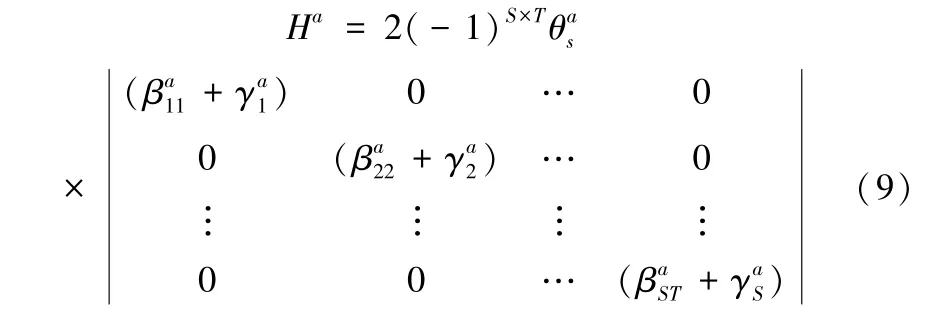
由于式(9)中海塞(Hessian)Ha的一阶顺序主子式:二阶顺序主子式,以此类推,故海塞矩阵Ha负定,可得船公司a的收益函数Πa是关于决策变量的严格凹函数。且约束条件式(3)、式(4)和式(5)都是线性函数,因此运价策略集合是凸集,因此,模型M是关于集装箱运价策略集的凸规划问题,得证。

本文关心的核心问题是在博弈双方均考虑竞争对手定价策略的情形下,纳什均衡策略集是否存在,以及是否唯一。有如下结论:

定理2模型M在每个时段存在唯一的纯策略纳什均衡。

证明:首先证明纯策略纳什均衡的存在性。根据纳什均衡存在定理[24],若对每一博弈参与者的策略空间都是非空紧凑凸集,收益函数关于其策略空间连续且是拟凹函数,那么存在纯策略纳什均衡。由于模型M的约束条件式(3)、式(4)和式(5)都是线性函数,故运价策略集是凸集。且由于,所以,运价策略集是紧凑闭凸集。此外,由定理1可知,模型M的收益函数Πa是关于pa的严格凹函数。由此可见,模型M满足纳什均衡存在定理,故模型M中至少存在一个纯策略纳什均衡。

再证唯一性。这里我们采用Cachon等[25]给出的方法来证明纳什均衡的唯一性。要证明均衡的唯一性就要验证船公司的收益函数是一个收缩映射(contraction mapping),而验证收益函数的收缩性等价于验证如式(10)海塞矩阵:式(10)是一个严格对角占优矩阵,即矩阵H中每个主对角元素的模都大于与它同行的其他元素的模的总和。其中,和分别为船公司1和船公司2的决策变量。

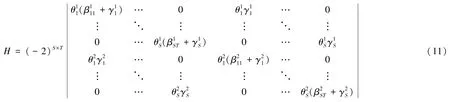
显然,对于式(11)中矩阵H的每个主对角元素的模都大于与它同行的其他元素的模的总和,即则H是一个严格对角占优矩阵,所以在模型M中在每个时段存在唯一的纯策略纳什均衡。得证。

推论1如果两家船公司信息对称,则模型M存在唯一对称的纯策略纳什均衡。

证明:如果两家船公司信息对称,则有模型M为对称博弈。推论1可由定理2的证明方法得到,得证。

由定理1和定理2可知模型M是连续可微的严格拟凹函数,每个船公司的可行策略集是闭合凸集,根据文献[22],利用库恩-塔克(K-T)方法可以求解模型M,得到双寡头竞争博弈下两家船公司的纳什均衡策略。

船公司a的拉格朗日函数为:

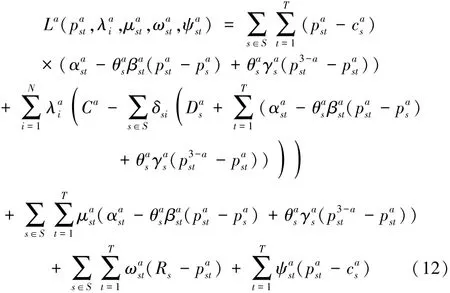
船公司a的K-T条件如下:

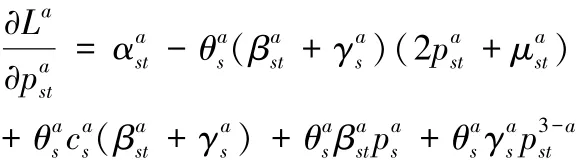
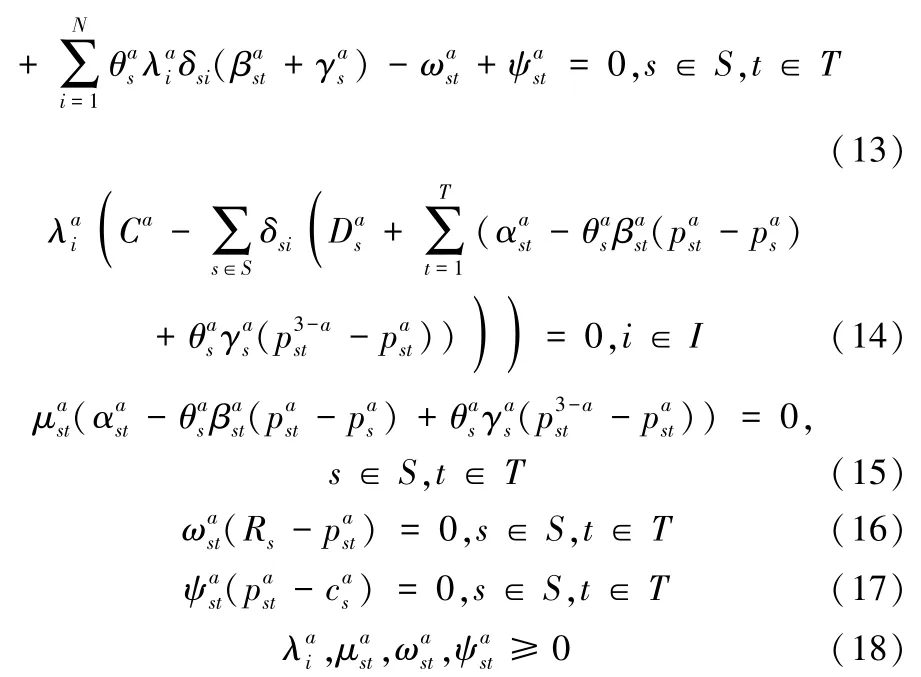
满足条件式(13)～式(18)为船公司a的K-T点。同样,可以推导出另外一家船公司的集装箱运价策略K-T点。

根据船公司a的K-T条件,可得如下性质:

(1)若船公司a在每个航段s的集装箱装载量均小于船舶容量,即:则必有拉格朗日乘子

因此,若任何航段s满足以上性质(1)～性质(3),则根据式(13)可得:

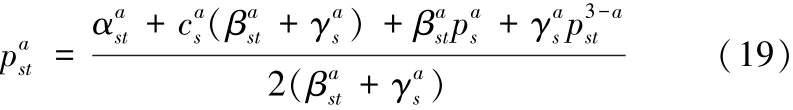
根据式(19),可求得两家船公司a=1和a=2即期市场客户的集装箱运价为:

若存在某个航段s不满足性质(1)～性质(3),将两家船公司a=1和a=2的K-T条件联立,可以得到两家船公司K-T条件组成的一个线性互补问题(LCP)[26-27]方程组为:

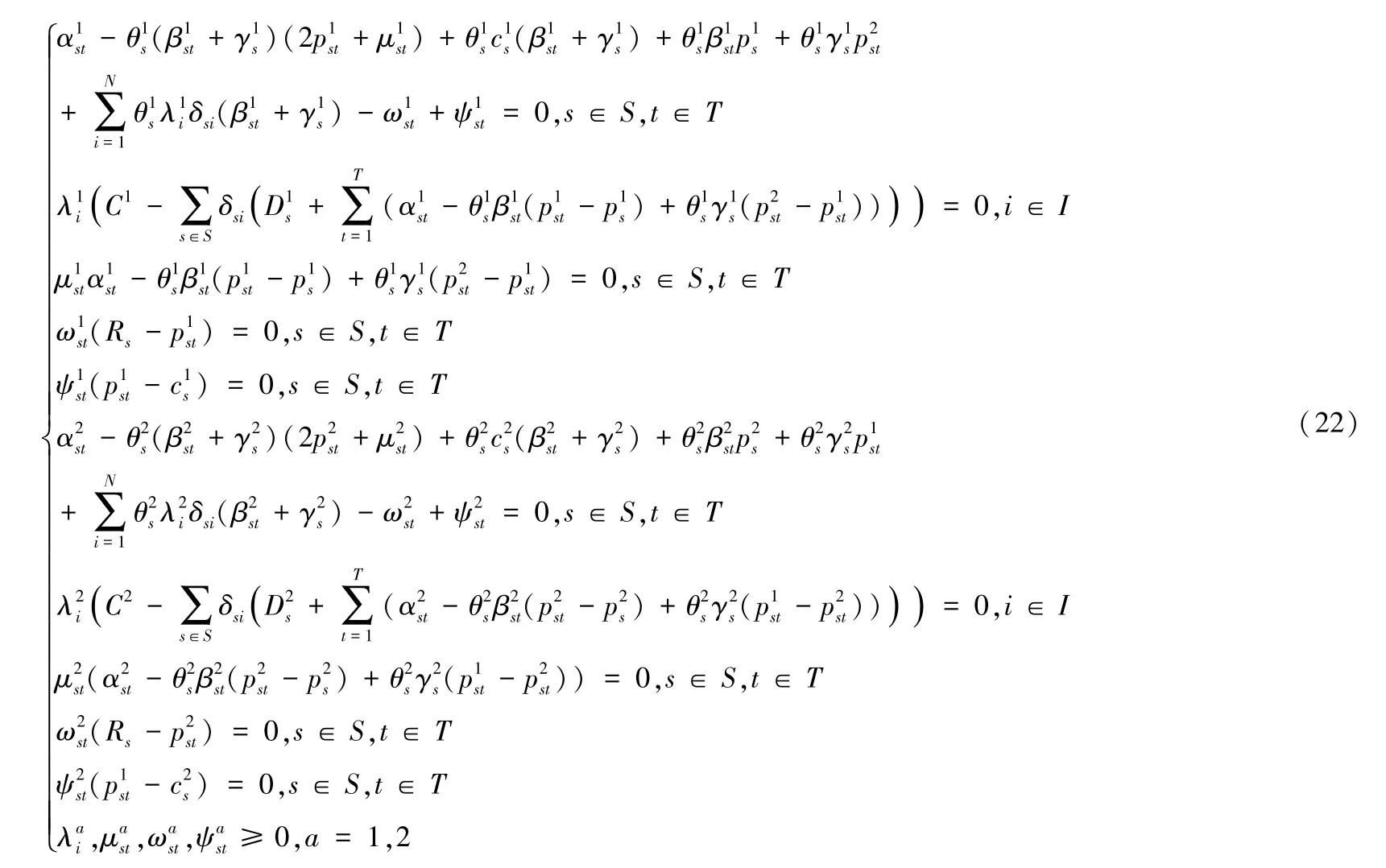
满足方程组式(22)及约束条件式(3)～式(5)的运价策略集记为¯,拉格朗日乘子记为。

定理3运价策略集是模型M的纳什均衡策略集。

证明:由定理1可知,任何一家船公司a的目标函数是严格凹函数;由定理2可知,船公司a的运价策略集的可行域是闭凸集,目标函数连续可微,约束条件式(3)～式(5)为线性函数,且连续可微,模型M的可行策略集是闭凸集。根据文献[22]中的定理4.6,则模型M的策略集为GNEP均衡策略。因此,运价策略集¯p是双寡头动态定价模型M的纳什均衡策略集,得证。

式(22)可以组成以下两个互补的向量:

将式(23)与约束条件式(3)～式(5)组成不等式方程组,利用Lingo等商业软件求解此不等式方程组[28],便可以得到双寡头动态定价模型M的纳什均衡策略集¯p。

3 算例分析

3.1 数据搜集

以AAC航线为例,某两家寡头船公司提供无差异的集装箱班轮运输服务,同时在跨太平洋区域,两家船公司都经营与AAC航线存在航段重叠的多条集装箱运输航线,如表1所示。参照网站https://www.clarksons.net上的船型信息,假设两家船公司在该航线上配置了装载量为10642TEU的集装箱船,两家船公司在各OD流长期合同客户的舱位需求信息已经通过历史数据统计得出,两家船公司在各OD流上的单位运输成本信息参照网站www.APL.com上的相关数据提取获得。两家船公司在即期市场的揽货时段为两周,即按周可以分成两个时段。表2给出了各OD流的信息,其中,船公司即期市场的运输需求量均值和在重叠航段上客户货物运输量分配比例系数均为船公司的商业机密,这里参照标准算例库LINER-LIB-2012[28]中的需求数据,对船公司即期市场的运输需求量均值暂作假设,按照各船公司合同客户市场货物需求数据,对重叠航段上客户货物运输量分配比例系数暂作假设,运价上限来自船公司公布的数据,即期市场客户的价格敏感系数和市场竞争强度参照文献[7,8]选取,具体数据如表2所示。

表2 OD流的信息Table 2 Information on the OD streams

3.2 计算结果与敏感性分析

应用Lingo11.0软件编程,选择global solver求解定价模型M,表3为双寡头竞争下(市场竞争强度=1)两家船公司在AAC航线上各港口对间两阶段的集装箱动态定价计算结果。

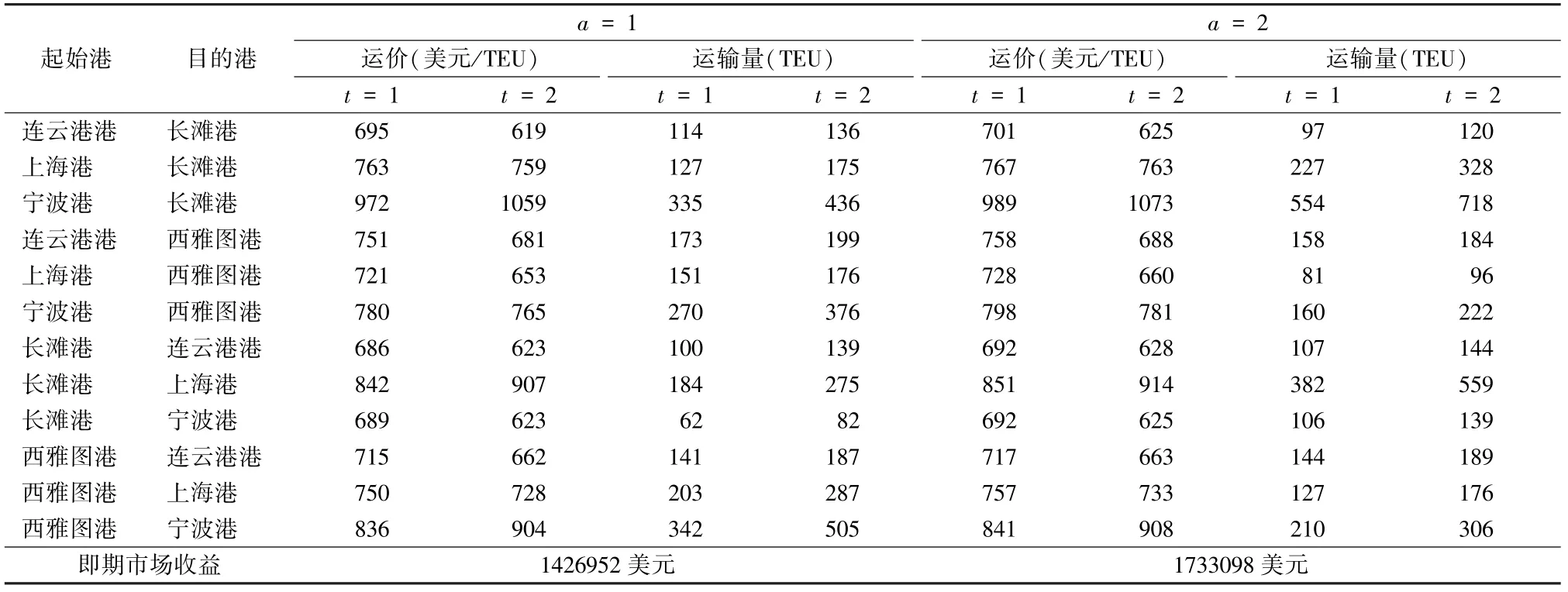
表3 集装箱动态定价计算结果Table 3 Calculation results of container dynamic pricing

由表3可以看出,在市场竞争强度1下,两家船公司t=1时段的运价均高于t=2时段的运价。原因在于,在供大于求的双寡头竞争市场环境下,集装箱运价成为船公司竞争的重点,船公司通过降低集装箱运价,可以提高船舶货物装载率及其自身的市场竞争力。

此外,由表3可见,采用本文设计的动态定价模型方法,船公司1和船公司2的即期市场收益分别为1426952美元和1733098美元。与文献[29]所评述的静态定价方法相比,船公司1和船公司2的即期市场收益分别增加了175032美元和294608美元。原因在于,本文基于收益管理的思想所构建的动态定价模型,能够根据不同时段双寡头即期市场需求的变化及客户的运价敏感度的不同,分时段动态地制定即期市场集装箱运价,这样可以更好地应对集装箱运输即期市场需求的波动性,显著地提高船公司的运输收益及市场竞争力。

在双寡头竞争环境下,即期市场客户的运价敏感度和竞争强度都是直接影响船公司即期市场集装箱运价及运输收益的关键因素。显而易见,客户的运价敏感度与集装箱运价呈负相关关系;市场竞争强度表示两家船公司竞争的激烈程度,越大,表示其中一家船公司每降低一个单位的运价从竞争对手吸引过来的市场需求越多。为了分析竞争强度对集装箱运价的影响,本文选取船公司1在上海港—长滩港两个往返航段上集装箱运价与市场竞争强度间的变化进行敏感度分析,结果分别如图2中a和b所示。

图2 上海—长滩往返航段市场竞争强度与运价变化趋势Figure 2 Shanghai-Long Beach round-trip leg market competition intensity and price change trend

由图2可以看出,上海港—长滩港之间的往返航段集装箱运价都随着竞争强度的增强而降低,当市场竞争强度较大时,随着竞争强度的增强,两个港口对间的往返集装箱运价不再随之有明显的降低;原因在于,在供大于求的市场环境下,为了提高船舶装载量及市场竞争力,集装箱运价成为船公司竞争的重点,两家船公司均会通过降低集装箱运价而吸引需求,以增加其船舶的装载量及运输收益,集装箱运价会随着竞争强度的增大而降低。但当运价降至到一定水平(如接近集装箱的单位运输成本)后,此时,船公司已没有多少降价空间。因此,当市场竞争强度较大时,运价降至到一定水平后,随着的增强,运价便不再明显降低。此外,图2还显示,当市场竞争强度较低时,t=2时段的集装箱运价高于t=1段的集装箱运价,而当市场竞争强度较大时,t=1时段的集装箱运价高于t=2时段的集装箱运价。这是由于,在市场竞争强度较低(即需求转移的可能性较低)、运价较高时,为了吸引客户需求,鼓励货主尽早订舱,船公司会给予较早订舱的客户一定的运价优惠。客户若在较晚时段订舱,则要承担较高的运价。而在市场竞争强度较强、运价较低时,在临近船期的较晚时段,为了提高船舶的装载率,船公司则会通过降价以提高市场竞争力和市场份额。不过还应看到,客户若在较早时段订舱,虽然比在较晚时段订舱时运价可能会略微高些,但却可以获得成功订舱的保障,相反,客户若在较晚时段订舱,虽然比在较早时段订舱时运价可能会低些,但却会面临一旦出现舱位不足集装箱有可能被拒载的风险。

为了进一步地分析客户运价敏感度及市场竞争强度对船公司收益的共同影响,本文参照文献[26],令即期市场客户运价敏感度在[0.6,1.5]范围内变化,参照文献[7,8],令市场竞争强度在[0,10]范围内变化,得到两家船公司的收益随着即期市场客户运价敏感度及市场竞争强度系数的变化趋势,分别如图3中a和b所示。

从图3可以看出:两家船公司的即期市场收益随着市场竞争强度的增大而降低,而收益降低的幅度会随着竞争强度的增大而出现明显的减缓趋势。客户运价敏感度对两家船公司即期市场收益的影响与市场竞争强度相关,当市场竞争强度较低(如图3中小于1)时,两家船公司即期市场收益随着客户运价敏感度的降低而增加;而当市场竞争强度较高(大于1)时,两家船公司即期市场收益随着客户运价敏感度的降低而降低。究其原因,是由于当市场竞争强度较低时,随着客户运价敏感度的降低,此时,若船公司提高运价,不仅不会对客户需求产生较大影响,而且也不会造成较多市场需求流向竞争对手,因而使船公司即期市场收益得到明显增加。而当市场竞争强度较大时,为了保持客户市场需求份额,提高市场竞争力,船公司便会采取降价策略,随着客户运价敏感度的降低,若一家船公司降低运价,其竞争对手也会随之降低运价,两家船公司降价竞争直至达到一个纳什均衡点,此时,两家船公司的收益就都会减少。

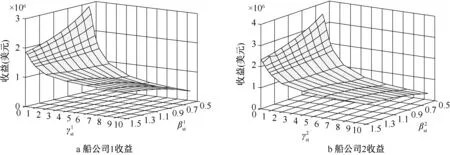
图3 客户运价敏感度及市场竞争强度对船公司收益的影响Figure 3 Impact of customer pricing sensitivity and market competition intensity on shipping company revenue

综合上述分析,可得如下研究结论和管理启示:

(1)在竞争激烈的双寡头集装箱班轮运输市场,船公司采用分时段动态定价有助于提高运输收益。因此,船公司可以根据即期市场客户的需求变化规律,将揽货期划分为若干个时段,对即期市场客户采取灵活的分时段动态定价策略,从而提高运输收益。

(2)船公司的运输收益与市场竞争强度呈负相关关系,集装箱运价随着双寡头市场竞争强度的增强而降低。因此,船公司之间加强联盟合作可以有效地降低市场竞争强度、避免价格战,从而提高运输收益。

(3)当市场竞争强度较低时,船公司的运输收益与客户运价敏感度呈负相关关系,而市场竞争强度激烈时,船公司的运输收益与客户运价敏感度呈现正相关关系。因此,船公司根据不同竞争市场下,运用即期市场客户运价敏感度对收益的影响,采取分时段定价策略,尽量降低一些揽货期临近截止的紧急客户运价敏感度对集装箱运输需求的不利影响,从而使船公司的运输收益得到更显著地提高。

4 结束语

本文基于收益管理的思想,结合班轮联盟经营实际,依据船公司经营多条航线且存在重叠航段的情形,研究了两家寡头船公司在同一竞争航线上,考虑货物多OD流的集装箱班轮运输动态定价问题,构建了双寡头竞争即期市场集装箱班轮运输分时段动态定价模型,并设计了相应的求解算法,算例分析验证了模型和算法的有效性和适用性。

本文的创新性工作主要包括:(1)结合班轮运输船舶多港挂靠运营实际和客户分类特征,将班轮运输动态定价问题研究由单OD流深化扩展到多OD流情形,提出了考虑多OD流的即期市场动态定价策略。(2)在班轮运输寡头竞争的市场环境下,将单航线班轮运输问题扩展至网络多航线问题,提出了考虑重叠航段的分时段动态定价策略。(3)提出并验证了广义纳什均衡更适合于描述实际班轮运输寡头竞争市场,K-T条件方法是求解双寡头竞争市场班轮运输动态定价的有效方法。这些创新性研究不仅提升了班轮运输动态定价模型的实用性,而且还能有效提高船公司的收益。

在集装箱班轮运输中,还存在寡头船公司在干/支线联运网络竞争的情形。因此,下一步研究可扩展到双寡头干/支线联运网路竞争市场集装箱班轮运输动态定价问题。