应急条件下危险医疗废物管理系统的网络设计

董乾东 李 敏

(南京大学 工程管理学院,江苏 南京 210093)

0 引言

突发的自然灾难或人为因素引起的灾难严重影响着人们的生命安全,如果不及时得到有效控制,将会导致全球性的危机。最近二十年间,已爆发数起致命的传染病,如2003年的非典型肺炎(SARS)、2009年的H1N1流感及2014年的埃博拉病毒等,都夺去了许多生命,严重影响了经济的发展,引起了全球性的恐慌。随着医疗体系和经济的发展,寻求医疗救治的人数急剧增加将导致医疗废物爆炸性增长,预计到2030年即使没有大规模流行病爆发,医疗废物的数量也将会比2018年增长超过50%[1]。2020年,全球多个国家遭受新冠肺炎的危害。根据世界卫生组织(WHO)的数据[2],截至2020年11月29日,全球累计确诊病例已超过6180万,死亡人数已超过140万。为了有效预防新冠肺炎的传播,妥善处理短期内急剧增加的危险医疗废物是至关重要的。为此要系统地考虑废物管理问题,包括废物的产生、收集、运输、回收和处置、回收资源的再利用以及残留物的处置等,以减少对经济和环境的危害[3]。例如巴西在新冠疫情期间超过35%的危险医疗废物没有妥善处理增加了新冠病毒传播的风险,同时由于循环利用项目的暂停导致经济和环境额外的双重损失[4]。与普通废弃物不同,医疗废物尤其在流行病期间具有很强的传染性,处理不及时将对环境和经济产生更加严重的影响。和传统的医疗废物管理系统网络设计相比,应急条件下的医疗废物管理系统网络设计面临的问题主要包括时间周期较短,一般只有几周到几个月;待处理的医疗废物的数量主要和流行病传播的速度密切相关,不确定性较大;为了有效并且及时地处理产生的大量医疗废物,需要快速、灵活地设置临时处理中心。因此,设计危险医疗废物管理系统网络,以便及时有效地处理疫情期间产生的医疗废物有着重要的现实意义,一方面降低了因医疗废物带来的风险传播,另一方面节约了经济成本。此类问题即为多目标优化问题,需要平衡多个可能相互冲突的目标,增加了决策的难度。

国外已有一些文献对危险废物网络设计问题进行了研究。Alidi[5]针对一种危险废物,以最小化成本为目标构建整数目标规划模型。Boyer等[6]针对工业危险废物选址运输问题构建混合整数规划模型,以总成本和总风险为目标函数,采用加权求和法进行求解。Cappanera等[7]构建以最小化成本为目标的选址运输模型,采用基于拉格朗日松弛的启发式算法进行求解。Current和Ratick[8]把公平性引入到模型中,指出运输问题和选址问题相互关联,采用加权求和法进行求解。Emek和Kara[9]研究了垃圾处置中心的选址问题,考虑环境污染因素,以最小化成本为目标构建整数规划模型,通过高斯扩散方程量化了空气污染浓度。Samanlioglu[10]针对工业危废管理问题,以最小化成本和风险为目标构建多目标选址模型,利用增广加权契比雪夫法求解。Ghezavati和Morakabatchian[11]研究了工业危险废物网络设计问题,通过考虑顾客满意度水平拓展了文献[10]的研究。Wyman和Kuby[12]考虑成本、风险和公平性等因素构建混合整数规划模型,解决危险废物网络选址和物流配送问题,采用加权求和法求解。同样考虑了选址公平性问题,Giannikos[13]构建了目标规划模型,并且通过引入单调递增惩罚函数改进目标规划方法,获得了相对满意解。Mantzaras和Voudrias[14]以传染性医疗废物为研究对象构建单目标优化模型,利用Evolver和Crystal ball进行求解。Alumur和Kara[15]针对危险废物管理问题构建了以最小化成本和风险为目标的优化模型,采用相对简单的线性加权求和方法进行求解。上述研究主要集中在工业危险废物的处理,而对医疗废物的研究较少。受SARS等流行病的影响,少数学者开始研究危险医疗废物的处理。Büyüktahtakın等[16]同时考虑流行病传播规律和物流问题,建立了流行病-物流混合整数规划模型,在预算限制的条件下最小化风险。Taslimi等[17]分析了收集和运输医疗废物过程中产生的风险,提出了基于分解思想的启发式算法。Lowe等[18]定性分析了Nebraska biocontainment unit(NBU)通过穿透式高压灭菌的方式对埃博拉病毒感染的医疗废物进行处理。Chiang等[19]统计SARS期间台北的医院产生的危险医疗废物数量,发现SARS患者平均每天产生的医疗废物显著增加,超过平时正常水平的四倍。上述文献只研究了一种危险废物,或单时间周期情形下的危险废物管理问题,且大多数模型采用简单的线性加权求和法求解。还有部分文献仅考虑了成本。实际上,危险废物管理系统的网络设计问题中除经济成本外,风险等也是不容忽视的关键因素。

另一方面,国内对危险废物管理系统的网络设计研究相对较少,多数文献研究应急情况下灾后救援物资配送网络设计问题。王苏生等[20]基于灾后救援过程中的物资分配问题构建双层规划模型,并采用竞争缓解策略解决双层规划求解时间较长问题。陈莹珍和赵秋红[21]则从公平的角度研究救援物资分配问题,通过供应与需求比率和物资满足率之间的正相关关系刻画公平性,利用启发式方法求解所构建模型。王新平和王海燕[22]考虑多个疫区的情况下,研究应急物资调度问题,通过遗传算法对仿真算例进行求解。同样研究灾后应急救援,王海军等[23]则以最小化成本和风险为目标,考虑多种车辆分析设施选址和配送路径问题,采用遗传算法求解构建的混合整数规划模型。郑斌等[24]考虑多式联运问题构建双层规划模型,以运输时间和物资分配公平性为优化目标,通过遗传算法求解。王雷等[25]则以时间和成本为目标函数构建数学模型,解决恐怖袭击过程中的警务调度问题,采用遗传算法进行求解。只有少数文献从定性的角度对危险医疗废物进行分析,罗兰等[26]通过归纳分析全国各个地方的医疗废物处理情况指出我国医疗废物管理系统缺乏回收环节,应该效仿日本等国家建立相应的回收系统。同样采用定性分析的方法,谭庆等[27]分析了武汉火神山医院医疗废物处理遇到的问题,指出由于医疗废物管理系统的不完善,比如没有灵活建立临时的医疗废物存储或处理中心,短时间内患者的急剧增加导致医疗废物堆积。蔡洪英等[28]以疫情期间重庆市的危险医疗废物处理为分析对象,指出面对巨量的危险医疗废物,必须安排专人二十四小时至少收集并处置一次。

综上所述,现有关于危险废物网络设计问题的文献仅有少数考虑了多时间周期情形,很少从定量角度系统地分析危险医疗废物管理问题。少数考虑多时间周期的研究分析的主要是较长时间周期(年)的情况,缺少基于短时间周期(流行病等特殊事件要求)对危险医疗废物管理问题进行的研究。此外,大多数应急物流网络设计的研究主要涉及救援物资物流网络设计问题,即使少数关于危险废物网络设计问题的研究也仅考虑一种危险废物及一种处理技术,但现实生活中存在多种危险废物,并且每种危险废物需要不同的处理技术。本文考虑到疫情期间危险医疗废物的高传染性,以最小化总成本和总风险为目标构建了多目标混合整数规划模型,同时考虑现实情况中网络节点处理能力有限、危险医疗废物种类和相应处理技术匹配、短时间周期内(天)危险医疗废物需清零等约束。本文构建的模型在处理危险医疗废物管理系统的网络设计问题方面更具一般性。另外,很少有研究使用实例验证危险医疗废物管理系统网络模型在实践中的可行性和有效性,而且多数使用的求解方法是启发式方法或加权求和法。本文以中国武汉新冠肺炎疫情为算例,采用加权求和法、增广加权契比雪夫法和增广ε约束法求解,并对比三种方法的数值表现。

1 问题描述及模型构建

1.1 问题描述

本文考虑的应急条件下危险医疗废物网络设计问题主要包括设施选址、危险医疗废物运输及处理技术选择和回收等问题(详见图1)。涉及的网络节点主要包括:医院、危险医疗废物临时及已有处理中心、循环利用中心和垃圾处置中心。医院会产生多种危险医疗废物,国家卫生和计划生育委员会发布的《医疗废物分类目录》将医疗废物分为感染性废物、病理性废物、损伤性废物、药物性废物和化学性废物。根据《医疗废物管理条例》,医疗机构治疗的病患产生的生活垃圾也视为医疗废物。一般来说,医疗部门产生大量不同种类的医疗废物,主要包括废弃的外科手套、手术器械、用于打针或抽血的针头、口罩、防护服、护眼用具(护目镜或面罩)、其他个人防护设备和药品等。不同种类的危险医疗废弃物通常有不同的最大储存时间限制,例如在新冠肺炎疫情期间,武汉市规定新冠肺炎患者产生的危险废弃物在医院的最大储存时间是24小时。危险医疗废物不能简单地采用焚烧或填埋的方式统一处理,一方面因为金属等类别的医疗废物不适合焚烧或填埋,另一方面因为用于垃圾处置的资源有限,需要多种处理方式分流,共同解决危险医疗废物的处理问题。为充分降低传染的风险,本文将医院及病患产生的各种医疗废物经过集中收集之后分类为可循环利用部分和待处理部分。可循环利用部分包括手术器械等不适合通过焚烧和掩埋等方式处理的金属类废弃物,此类废弃物经过严格消毒杀菌之后可以重复使用,既节省了经济成本,又减轻了垃圾处置中心的压力。待处理部分包括口罩、外科手套、防护服、用于抽血或打针的针头、病患生活用品等,此类医疗废物通过消毒杀菌处理之后分为可循环利用部分和待处置残渣。所有危险医疗废物均需要经过垃圾处理中心或垃圾循环利用中心进行消毒杀菌处理,每个时间周期期末(例如24小时)医院、处理中心和循环利用中心的医疗废物均需清零,实现日产日清。如果危险医疗废物不及时处理,尤其对医院而言,人口比较密集,可能会产生交叉感染,而且占用医院有限的空间资源。考虑到垃圾处置中心一般都处在较偏远的地方,人口密度较低,每个时间周期期末可以储存部分未被处理的危险医疗废物。可循环利用的部分直接运送到循环利用中心做进一步处理,待处理部分运送到已有或临时处理中心进行处理。已有的或临时的处理中心处理危险医疗废物时须使用与之相匹配的处理技术进行处理,如微波、化学或高温高压等消毒方式。经过危险医疗废物处理中心和循环利用中心处理后产生的医疗垃圾残渣直接运送到垃圾处置中心进行最终的焚烧或填埋处理。

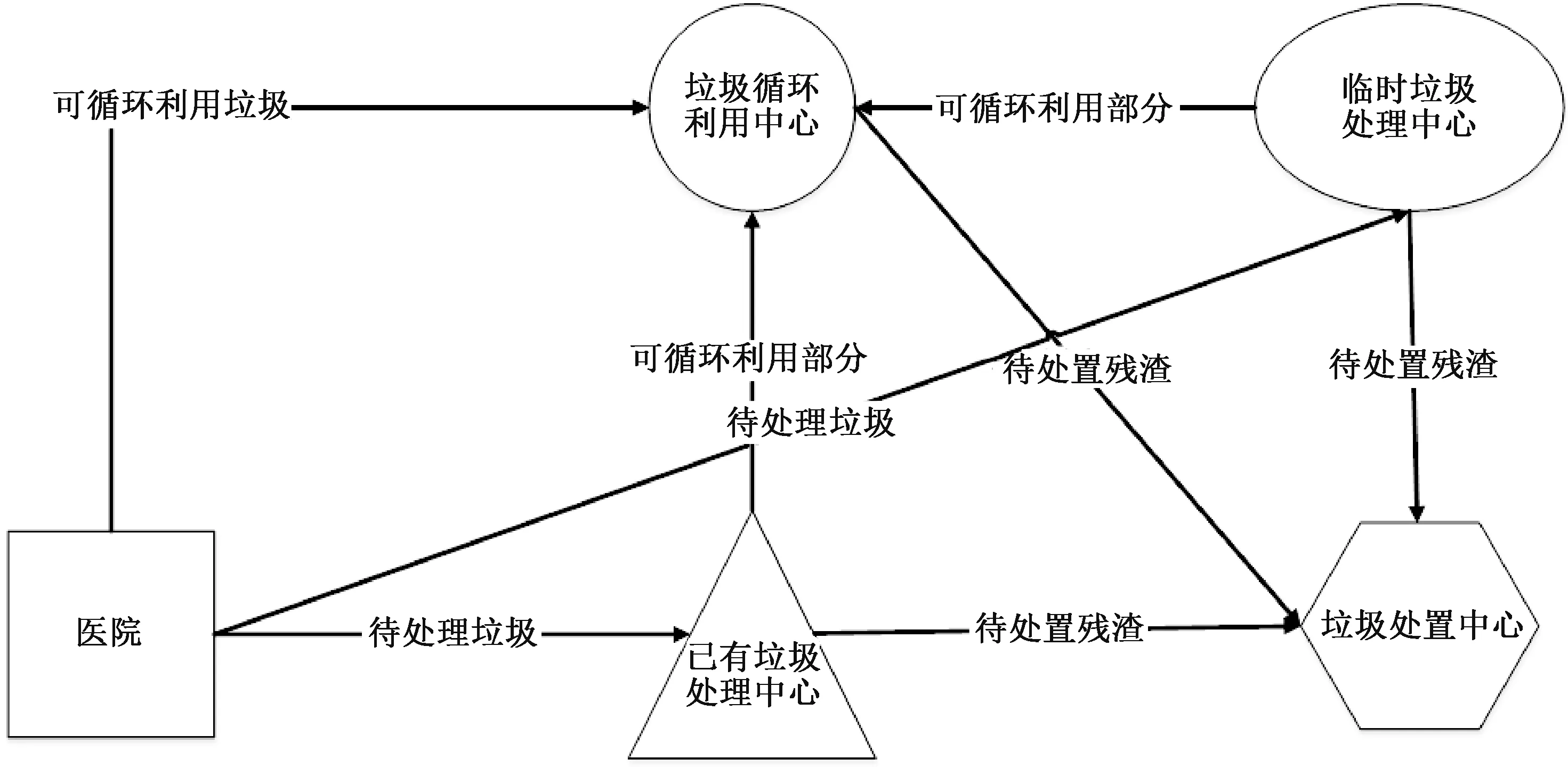
图1 危险医疗废物管理网络Figure 1 Hazardous medical waste management network

本文要解决的主要问题为:医院产生的多种类别且数量递增的危险医疗废物在短时间内(例如每天)运输及处理问题;为了及时处理大量危险医疗废物,临时处理中心、循环利用中心和垃圾处置中心的选址问题;每个时间周期开放及运营临时处理中心和循环利用中心的选取问题;当临时处理中心开放时,需要具备的处理技术问题;各网络节点的处理能力及回收等因素对危险医疗废物的管理产生的影响等问题。

本文考虑的总成本包括运输成本,各个循环利用中心、已有或临时处理中心和垃圾处置中心的处理成本,临时处理中心及循环利用中心的开放和运营成本,已有处理中心和垃圾处置中心的运营成本等。医院等网络节点的危险医疗废物存在感染周围居民的风险,而且危险医疗废物的运输对道路两旁的居民同样产生感染的风险。因此总风险包括医院、处理中心、循环利用中心等在处理及运输危险医疗废物过程中产生的风险。为使设计的危险医疗废物管理系统网络更加经济且对环境造成的负外部性最小(即风险最小),本文考虑以下几种约束。首先,危险医疗废物物料平衡,即每种危险医疗废物在各处理中心或循环利用中心进行处理,需满足输入量和输出量均衡。而且每个医院产生的危险医疗废物必须在要求的时间内得到处理,不允许有残存堆积。其次,考虑危险医疗废物处理中心、循环利用中心和垃圾处置中心最大和最小处理能力约束,而且临时处理中心和循环利用中心的开放和运营都要满足最小和最大处理能力约束。最后,已有处理中心或临时处理中心拥有的处理技术必须和待处理的危险医疗废物相匹配才能进行处理。

1.2 模型构建

考虑疫情期间产生的大量危险医疗废物需要及时且有效地处理,本小节基于多时间周期情形,对危险医疗废物网络设计问题进行研究,构建多目标混合整数规划模型。

为合理地构建模型,本文提出以下假设:(1)如果人口比较聚集,那么感染的可能性及传染速度增大;危险医疗废物数量较多时,则携带的病毒数量增多的可能性增大。因此假设危险医疗废物在运输及处理过程中产生的风险和人口密度、运输距离及危险医疗废物的数量正相关,且具有可加性;(2)考虑到应急条件下资源的稀缺性和疫情持续时间的短暂性(一般几周或几个月),如果在某个时间周期之后关闭网络节点意味着资源的重新分配和移动,不利于危险医疗废物的管理。因此,为加强资源利用率,临时危险医疗废物处理中心或循环利用中心如果开放,余下的时间周期均要使用;(3)类似文献[10]和[15],假设运输成本和运输距离及载重相关,运营成本和处理的危险医疗废物数量线性相关。

本文采用字母加不同的上下标表示参数和变量。使用符号说明如下:

集合:

H:医院h的集合;

T:危险医疗废物处理中心t的集合;

P:时间周期p的集合;

S:危险医疗废物循环利用中心s的集合;

R:临时危险医疗废物处理中心r的集合;

D:危险医疗废物处置中心d的集合;

V:网络节点v的集合,V⊆{T,R,S};

W:危险医疗废物种类w的集合;

L:危险医疗废物处理技术种类l的集合。

参数:

Qhpw:时间周期p医院h产生的危险医疗废物w的数量;

Nhp:时间周期p医院h的病人数量;

chvp:时间周期p从医院h运送危险医疗废物到网络节点v∈{t,r,s}的单位成本;

ctsp:时间周期p从处理中心t运送危险医疗废物到循环利用中心s的单位成本;

crsp:时间周期p从临时处理中心r运送危险医疗废物到循环利用中心s的单位成本;

cvdp:时间周期p从网络节点v∈{t,r,s}运送危险医疗废物到垃圾处置中心d的单位成本;

dhv:医院h与网络节点v∈{t,r,s}的距离;

dvs:网络节点v∈{t,r}与循环利用中心s的距离;

dvd:网络节点v∈{t,r,s}与垃圾处置中心d的距离;

:从医院h到已有处理中心t运输路径存在的人数;:从医院h到网络节点v∈{t,r,s}运输路径存在的人数;

:从网络节点v∈{t,r}到循环利用中心s运输路径存在的人数;

:从网络节点v到垃圾处置中心d运输路径存在的人数;

:网络节点v∈{t,r,s}周围存在的人数;

:从医院h到网络节点v∈{t,r,s}运输危险医疗废物存在风险的概率;

:从网络节点v∈{t,r}到循环利用中心s运输危险医疗废物存在风险的概率;

:从网络节点v∈{t,r,s}到垃圾处置中心d运输危险医疗废物存在风险的概率;

:网络节点v∈{t,r,s}运营时周围存在风险的概率;

:时间周期p网络节点v∈{t,r}采用技术l的最大处理能力;

:时间周期p循环利用中心s的最大处理能力;

:时间周期p垃圾处置中心d的最大处理能力;

bvpl:时间周期p网络节点v∈{t,r}采用技术l的最小处理能力;

bsp:时间周期p循环利用中心s的最小处理能力;

bdp:时间周期p垃圾处置中心d的最小处理能力;:时间周期p网络节点v∈{t,r}采用技术l的单位处理成本;

:时间周期p循环利用中心s的单位处理成本;

:时间周期p垃圾处置中心d的单位处理成本;

frpl:时间周期p开放配置处理技术l的临时处理中心r的固定成本;

fsp:时间周期p开放循环利用中心s的固定成本;

ovpl:时间周期p配置处理技术l的网络节点v∈{t,r}的运营成本;

osp:时间周期p循环利用中心s的运营成本;

odp:时间周期p垃圾处置中心d的运营成本;

κhpw:时间周期p医院h运出的危险医疗废物w待处理比例;

αtlw:已有处理中心t采用处理技术l处理危险医疗废物w的可回收比例;

βsw:经循环利用中心s处理的危险医疗废物w的残余比例;

γrlw:临时处理中心r采用处理技术l处理危险医疗废物w的可回收比例。

决策变量:

yrpl:等于1时表示在周期p开放配置处理技术l的临时处理中心t,否则等于0;

ysp:等于1时表示在周期p开放循环利用中心s,否则等于0;

uvpl:等于1时表示在周期p使用配置处理技术l的网络节点v∈{t,r},否则等于0;

usp:等于1时表示在周期p使用循环利用中心s,否则等于0;

udp:等于1时表示在周期p使用垃圾处置中心d,否则等于0;

λlw:等于1表示危险医疗废物w可以被处理技术l处理,否则等于0;

xhvpw:时间周期p从医院h运送到网络节点v的危险医疗废物w的数量;

xvspw:时间周期p从网络节点v∈{t,r}运送到循环利用中心s的危险医疗废物w的数量;

xvdpw:时间周期p从网络节点v∈{t,r,s}运送到处置中心d的危险医疗废物w的数量;

zvplw:时间周期p网络节点v∈{t,r}采用处理技术l处理的危险医疗废物w的数量;

zspw:时间周期p循环利用中心s处理的危险医疗废物w的数量;

zdpw:时间周期p处置中心d处理的危险医疗废物w的数量;

:时间周期p处置中心d未被处理的危险医疗废物w的数量。

本文建立以下混合整数规划模型,记作MIP(mixed integer programming):

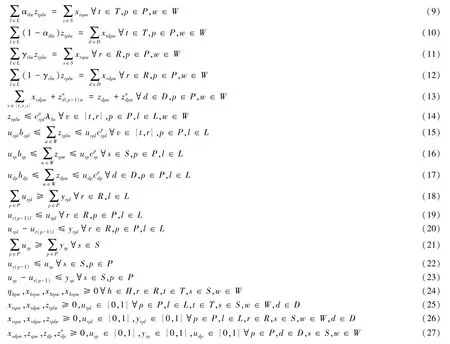
其中函数f1和f2分别表示设施选址和医疗废物运输及处理过程中产生的总风险和总成本。总风险包括各网络节点之间运输危险医疗废物产生的风险和处理危险医疗废物产生的风险。总成本包括网络节点间的运输成本、运营成本、临时节点的开放成本和处理危险医疗废物的变动成本。约束(3)表示医院产生的危险医疗废物的质量平衡。约束(4)和(5)表示运输的危险医疗废物待回收部分和待处理部分的质量平衡。考虑到流行病的高传染性,所有危险医疗废物均需要被处理。约束(6)表示循环利用中心危险医疗废物的质量平衡。约束(7)表示经循环利用中心处理之后不能回收再利用的残余。约束(8)表示已有处理中心和临时处理中心的危险医疗废物质量平衡。约束(9)和(10)表示经过已有处理中心处理之后可以回收再利用部分和残余。约束(11)和(12)表示经过临时处理中心处理之后可以回收再利用部分和残余。约束(13)表示垃圾处置中心的危险医疗废物质量平衡。约束(14)表示已有处理中心和临时处理中心的危险医疗废物处理技术要和待处理的危险医疗废物种类相匹配。约束(15)～(17)分别表示循环利用中心、已有处理中心、临时处理中心和垃圾处置中心的处理能力约束。约束(18)和(21)确保临时处理中心或循环利用中心被使用的次数多于开放的次数。约束(20)和(23)表示临时处理中心或循环利用中心如被使用,那么该中心必须是开放的;同时确保不重复开放。考虑应急条件下资源有限和时间周期较短,约束(19)和(22)表示临时处理中心或循环利用中心如被使用,那么该处理中心就要运营到时间周期结束。约束(24)～(27)表示各个决策变量是非负或0-1变量。

由于本文的单目标问题可以归类为能力受限的设施选址问题,这类问题已在一些研究中被证明是NP难问题[29],因此本文所研究的问题是NP难的,需要选择合适的数值算法求解。

2 数值算法

上节构建的模型MIP(1)～(27)为多目标混合整数规划模型,而决策者很难明确辨别多个目标之间的相对重要性。本文所考虑的问题涉及的目标函数(经济成本和风险)相互冲突,不存在唯一最优解。因此,需要求解出一组有代表性的非支配解,决策者再根据个人偏好、具体的实际管理问题进行选择。已有研究提出了求解多目标优化问题的数值算法,但这些方法的数值表现很大程度上依赖于模型的质量[10,11,13]。数值表现较好的求解多目标优化问题的方法可以求得更多的分布较为均匀的差异解。本节根据所构建的多目标混合整数规划模型的特点,采用三种算法进行求解,并对数值表现进行比较。

本文模型可以简化为minf(x)={f1(x),f2(x)} s.t.x∈X,其中f1(x)和f2(x)分别表示总成本函数和总风险函数,可行域X由约束(3)～(27)确定。由于f1(x)和f2(x)的量纲不同,需要利用归一化方法统一,即表示第i个归一化后的目标函数,和分别表示第i个目标函数的最小值和最大值。为理想点(utopia point),fmax=(fmax1,fmax2)为帕累托解的上界(nadir point)。通过分层序列法求得帕累托解的上界,即和

2.1 加权求和方法

加权求和方法[30]是求解多目标优化问题的传统方法之一。这种方法利用非负权重将多目标问题转化为单目标问题,通过调节权重求得非支配解。针对本文模型MIP,定义λ1≥0和λ2≥0(λ1+λ2=1)分别为总风险和总成本的权重。经过归一化处理之后,模型MIP可以转化为:

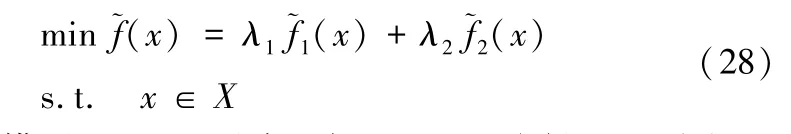
对上述模型(28),通过在区间[0,1]上取得i+1个权重向量求得i+1个非支配解。令j=0,…,i,可以得到权重λ1=1-j/i和λ2=1-λ1。求解模型(28),得到最优解x*,进而得到原模型MIP的非劣解(f1(x*),f2(x*))。由于标准化处理时导致目标函数值~(x)太小,所以本文在求解模型时用~(x)替代~(x),θ为足够大的数,以使该算法有更优的数值表现。已有文献Koski等[31]表明,加权求和方法虽然操作简单,但是存在一些不足。例如求得的非劣解分布不均匀;当非支配解构成的区域是非凸域时,加权求和方法找不到非支配解。

2.2 增广ε约束方法

增广ε约束方法最早由Haimes等[32]提出,后经Mavrotas和Florios[33]引入互补松弛变量对其进行优化,目前已经被广泛应用到生产制造、物流等领域进行多目标问题的求解。针对本文所构建模型的增广ε约束方法具体实现过程如下:

步骤1确定目标函数最小值f1min和最大值f1max,计算v

步骤2求解i+1个非支配解,v被i+1个点分成长度为v/i并且相等的i个部分,初始化j=0,转入下一步。

步骤3如果j≤i,求解模型(29),否则终止。

其中μ为目标函数f1(x)的松弛变量,τ是一个充分小的正参数,λ1=1-j/i。

步骤4如果模型(29)存在最优解(x*,μ*),那么得到非支配解(f1(x*),f2(x*)),转入下一步,否则转入步骤6。

步骤5如果模型(29)中的松弛变量μ满足μ*＞v/i,那么接下来循环迭代产生的一些帕累托解是相同的。因此,为了提升效率,令,j=j+Δ,转入步骤3。

步骤6如果模型(29)找不到可行解,算法终止。

鉴于设定的i+1个点不能保证获得同样数量的帕累托解,因此如果要获得足够数量的非支配解,可以通过增大i实现。

2.3 增广加权契比雪夫方法

契比雪夫方法最早由Bowman[34]提出,后经Steuer和Choo[35]改进为增广加权契比雪夫法。针对本文模型MIP,令λ1≥0和λ2≥0(λ1+λ2=1)分别为总成本和总风险的权重,τ为充分小的正参数。模型MIP转化为:

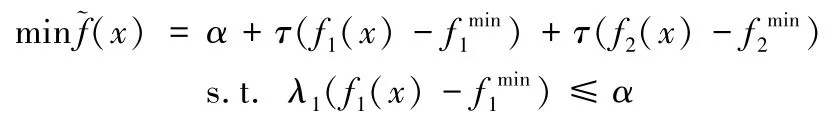
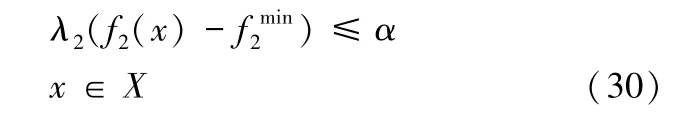
针对模型(30),欲求i+1个非支配解,需要在区间[0,1]上取得i+1个权重。令j=0,…,i,可以得到λ1=1-j/i和λ2=1-λ1。为使该方法数值表现更优,本文用~(x)替代,其中θ是一个充分大的常数。通过求解模型(30),得到其最优解x*,进而得到原模型的非支配解(f1(x*),f2(x*))。

3 数值实验

3.1 实例

本节以中国武汉在新冠肺炎疫情期间危险医疗废物管理系统网络设计为例,验证模型在实践中的有效性和可行性,同时采用第2节提出的多目标优化方法求解,获得危险医疗废物处理的最优方案,并进行敏感性分析。因为新冠病毒具有较强的感染性,潜伏期间患者没有明显的外部表现特征,而且武汉是交通枢纽,因此在短时间内感染人数急剧上升,产生的危险医疗废物也急剧增多。2020年2月,武汉设立了27个针对新冠肺炎患者的定点医院,另外新建雷神山和火神山2家临时医院和11家临时方舱医院,产生危险医疗废物的医院共40家(详见表1—表3)。医院产生的危险医疗废物数量和住院的新冠肺炎患者数量正相关。根据2018年武汉统计年鉴,每个病床每天产生大约0.6千克的危险医疗废物。考虑到新冠肺炎治疗的特殊性,本文假设每个新冠肺炎患者每天产生2千克危险医疗废物[36]。为了使危险医疗废物得到有效处理,武汉市一些垃圾转运中心转为危险医疗废物临时循环利用中心。医院、已有或临时危险医疗废物处理中心、循环利用中心和垃圾处置中心等网络节点的具体分布见图2,网络节点之间的距离通过百度地图获取。危险医疗废物运输过程中产生风险的概率为3.6*运输距离*10-7[36]。处理中心和循环利用中心发生风险的概率为πr2*人口密度[37],处理中心的感染半径设置为2千米,循环利用中心的感染半径设置为1千米。每家医院产生两种危险医疗废物(w1,w2),一类为通过焚烧等方式可以处理的,如衣物等;另一类为焚烧不能处理,需要消毒之后回收的,如金属医疗用品、不锈钢饭盒等。不同类别的危险医疗废物需要相应的技术(l1,l2)进行处理,具备不同处理技术的设备购置成本、处理成本以及处理能力不同。潜在网络节点有6个临时处理中心(r1-r6),4个已有处理中心(t1-t4),4个循环利用中心(s1-s4)和3个垃圾处置中心(d1-d3)。

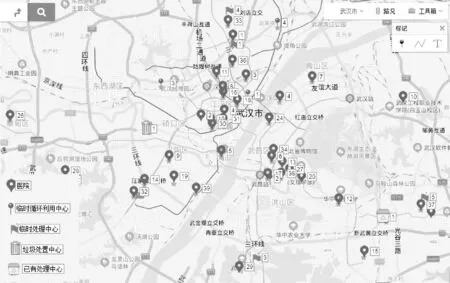
图2 网络节点分布情况Figure 2 Network nodes distribution

表1 临时危险医疗废物处理中心及人口密度Table 1 Temporary hazardous medical wastetreatment center and population density

表3 医院及病床数量Table 3 Number of hospitals and beds

表4～6是已有处理中心、临时处理中心和循环利用中心的相关参数,包括成本和处理能力数据等,数据是根据实际情况以及文献[38]获得。本文考虑的运输成本和运输距离、路况及载重有关,距离市区近时单位运输成本设置为35元/吨/千米[37],但距离市区较远时,考虑到人口密度相对稀疏,单位运输成本会有所下降,因此假设单位运输成本服从区间[30,35]上的均匀分布。

表4 临时危险医疗废物处理中心相关参数Table 4 Parameters of temporary hazardous medical waste treatment center

表2 临时循环利用中心及人口密度Table 2 Temporary recycling center and population density

采用第2节所提到的三种方法对算例进行求解,并且比较三种方法的数值表现,衡量指标为求得的非劣解个数、解的分布均匀性和计算时间,计算机的配置为Core i3/2.53GHz/Windows7。增广加权契比雪夫法和加权求和法中的参数θ设置为103,增广ε约束方法和增广加权契比雪夫法中的参数τ设置为10-3。求解结果见图3和表7。图3(a)是6个非支配解的分布情况,图3(b)是11个非支配解的分布情况。从图中可知,增广加权契比雪夫法和加权求和方法求解的非支配解集在真实帕累托前沿的右下方,即使随着解的个数增加,该缺点依然存在。而增广ε约束方法相比较于增广加权契比雪夫法和加权求和方法,求得的帕累托前沿分布更加均匀。表7是11个帕累托解和求解时间。从表7可知,增广加权契比雪夫法计算耗时最长,加权求和方法因其计算量小耗时最短,解的分布最均匀的是增广ε约束方法。因此,结合图3和表7可知,针对本文模型的求解,从解的分布均匀性和计算时间综合考虑,增广ε约束方法数值表现更优。

表7 帕累托前沿Table 7 Pareto front

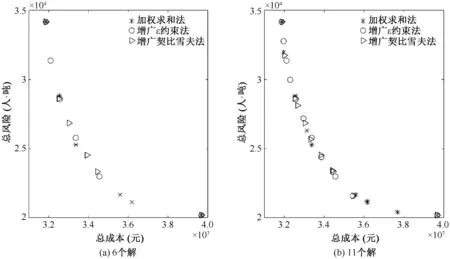
图3 帕累托前沿Figure 3 Pareto front

表5 已有危险医疗废物处理中心相关参数Table 5 Parameters of hazardous medical waste treatment center

表6 临时危险医疗废物循环利用中心相关参数Table 6 Parameters of temporary hazardous medical waste treatment center

表8是等权重时增广ε约束方法对算例的求解结果。从表8可知每个时间周期医院产生的多种医疗废物分配和处理情况。医院产生的危险医疗废物分别由已有处理中心1和临时处理中心1、3进行处理。医疗废物可回收的部分均由临时循环利用中心1回收处理。

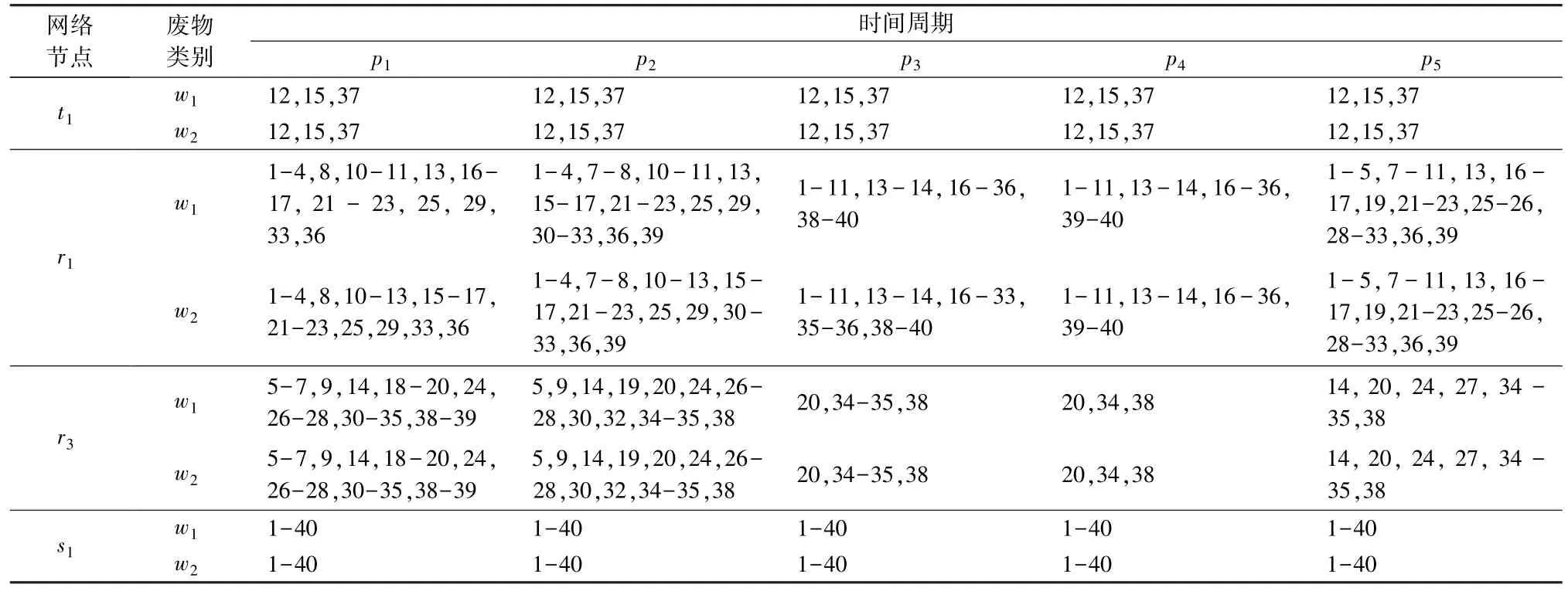
表8 医院的医疗废物分配情况(等权重)Table 8 Distribution of medical waste in hospital (equal weight)

3.2 敏感性分析

为使模型能够更合理地刻画现实场景,本文模型对已有的和临时的网络节点,包括处理中心和循环利用中心等,均设置最小处理能力和最大处理能力约束以确保网络节点都在合理的工作负荷范围内运行。本小节定义指标“处理能力比率”,即网络节点最小处理能力与最大处理能力的比值。将各网络节点的最大处理能力固定在最大值,分析最小处理能力的变化对危险医疗废物网络的影响。本小节设置处理能力比率从0.1增大到0.9,变化步长为0.1。

图4为网络节点处理能力比率的变化对总成本和总风险的影响。由图4可知,随着处理能力比率的增大,总成本单调递增。当处理能力比率小于0.2时,总成本没有变化,但当处理能力比率超过0.2 时,总成本逐渐增加,而且增速逐渐增大。与总成本情况不同,总风险随着处理能力比率增大呈现先不变后减小再增大的变化趋势。当处理能力比率小于0.2 时,处理能力比率的变化对风险没有影响。当处理能力比率在0.2到0.6之间变化时,风险逐渐减小。但当处理能力比率超过0.6 之后,风险逐渐增大。由此可知,网络节点处理能力比率的大小显著影响危险医疗废物管理系统网络的总成本和总风险。因此,决策者需要谨慎考虑危险医疗废物管理系统网络中各节点的处理能力,进而平衡经济成本和风险。当处理传染性较高的流行病(如新冠肺炎)产生的危险医疗废物问题时,可以优先考虑风险因素,其次再考虑成本,根据具体问题调整目标函数权重,进而更加合理、高效的解决危险医疗废物管理问题。

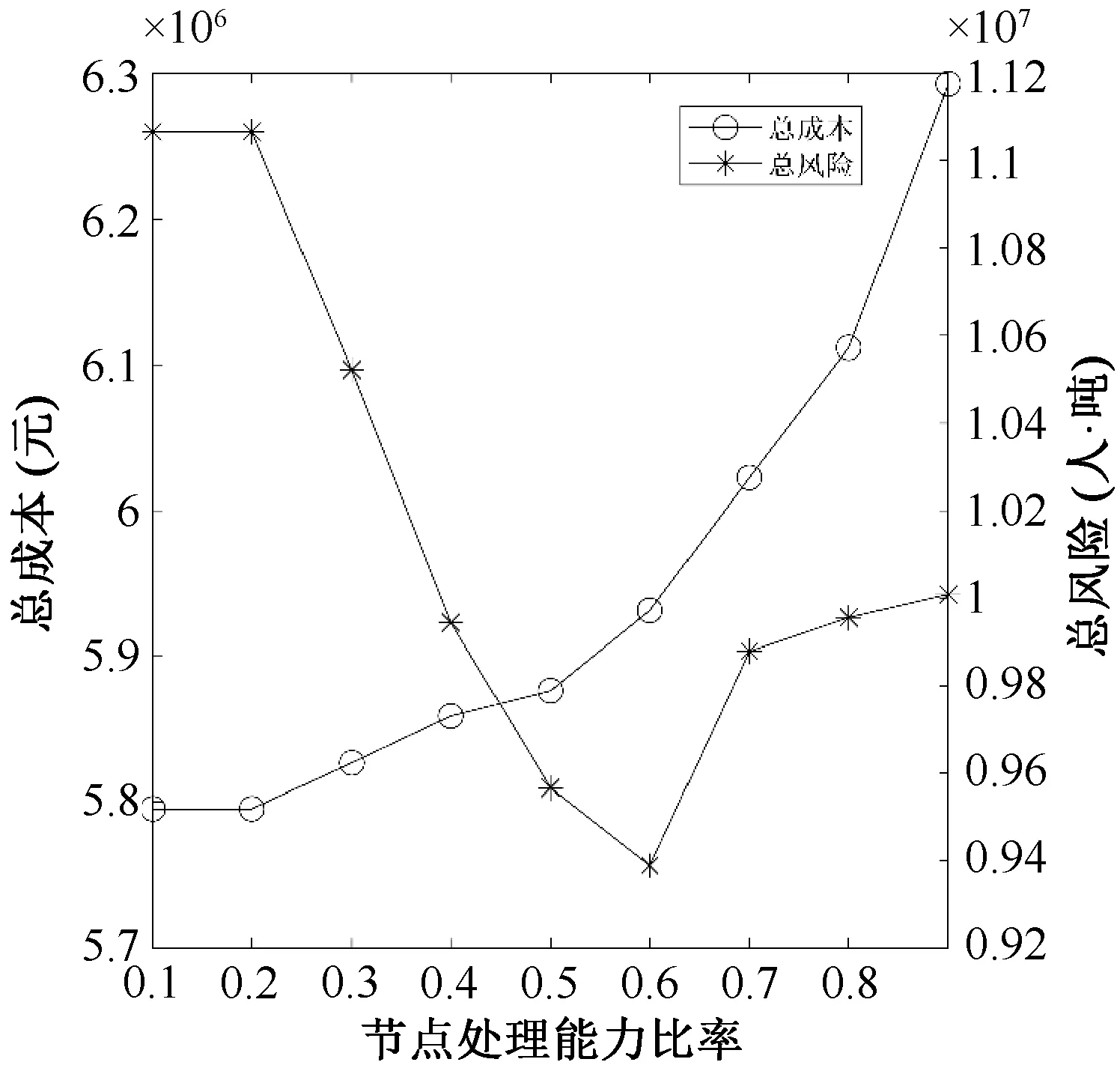
图4 节点处理能力对总成本和总风险的影响Figure 4 Impacts of nodes processing capacity on total cost and risk

图5是关于回收率对危险医疗废物管理系统总成本和总风险的影响,设置回收率从0.1增大到0.9,步长为0.1。由图5可知,总成本随着回收率的增大单调递减。当回收率小于0.3 时,总风险未发生变化,但当回收率超过0.4 时,总风险开始减少。原因是当回收的医疗废物较多时,与回收的医疗废物较少时相比网络节点的选择和使用发生变化,在运输距离、人口密度等因素的影响下,总风险变小。但当回收率超过0.7,总风险开始增大。因此,决策者可以通过调节危险医疗废物的回收率控制管理系统的总成本和总风险。

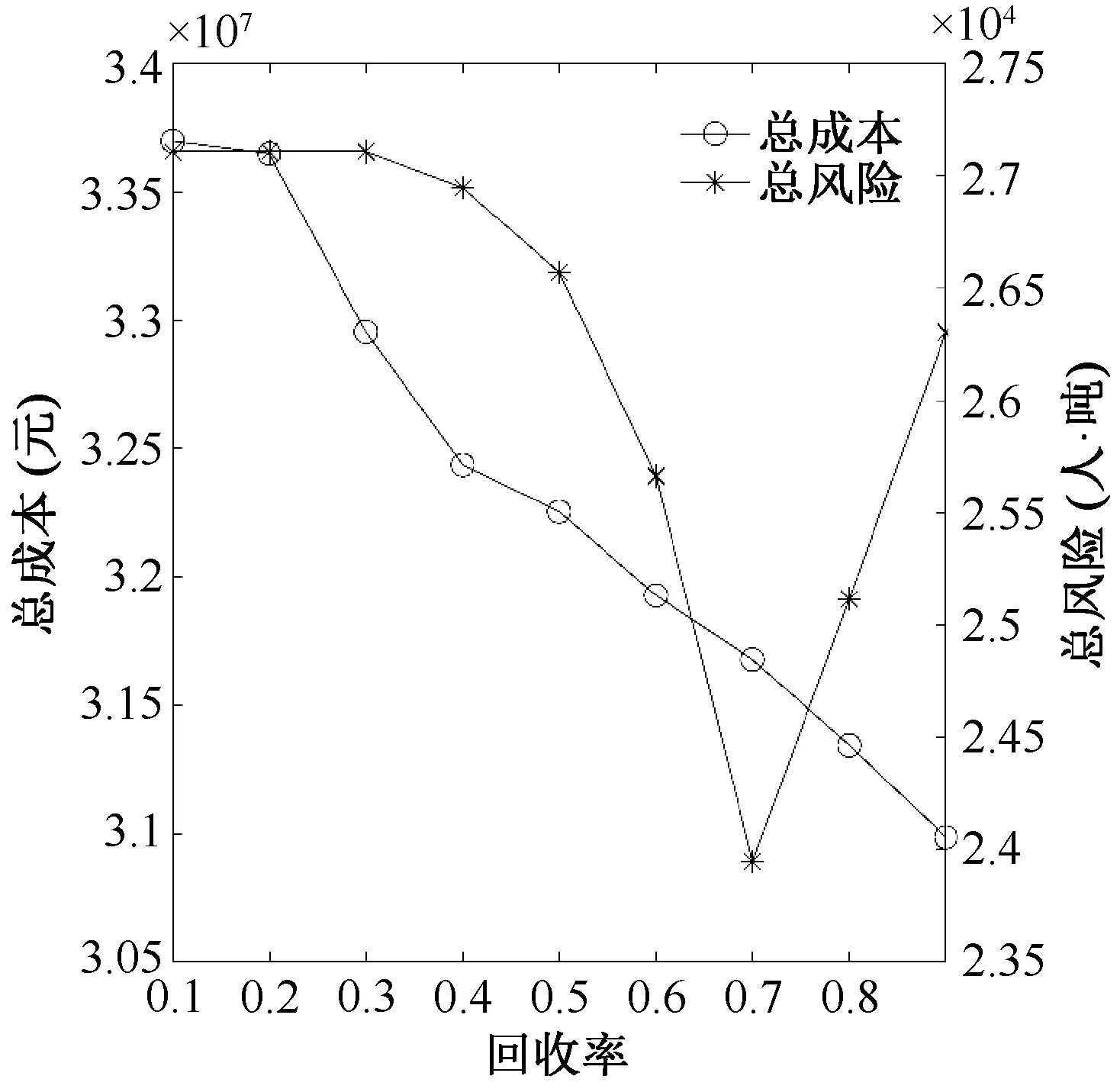
图5 回收率对总成本和总风险的影响Figure 5 Impacts of recovery rate on total cost and risk

3.3 管理启示

数值实验验证了本文提出的多目标混合整数规划模型在实践中的有效性和可行性,得到应急条件下危险医疗废物管理最优方案。数值实验结果揭示的管理及实践意义如下:

(1)根据数值实验结果可知,决策者在做多目标决策时几乎不可能同时实现多个决策目标最优,即通常得不到唯一最优解,只能得到帕累托最优解。本文采用的多目标优化方法很好地平衡了多个冲突的目标,得到帕累托最优解。相比较而言,增广ε约束方法在获取帕累托最优解的数量和分布均匀性方面的数值表现均优于加权求和法及增广加权契比雪夫法。决策者可以根据实际决策问题,设置合适的参数(权重等),从而得到相应的决策方案,达到相应的决策目标。

(2)采用本文提出的多目标混合整数规划模型,在应急条件下对危险医疗废物管理系统网络进行设计,得到医疗废物的处理方案,以实现总经济成本和总风险的平衡。当遇到流行病爆发等情形,决策者可以根据实际情况设置较大的风险权重,从而最大限度地降低风险。

(3)通过调整网络节点处理能力的比率控制总经济成本和总风险。总经济成本随着处理能力比率增大而增大,而且增加的速度不断增大;然而,总风险则随着处理能力比率的增大先减小,超过一定阈值时总风险随着处理能力比率的增大而增大。

(4)通过调节危险废物回收率改变总风险和总经济成本。随着回收率的增大,总成本逐渐减小;但总风险随着回收率的增大先减小,当回收率达到一定阈值时,总风险随着回收率的增大反而会增大。

4 结语

本文基于新冠肺炎疫情对危险医疗废物管理系统的网络设计问题进行研究,考虑多时间周期、多种医疗废物及处理技术和回收等因素,解决了包括危险医疗废物处理设施选址、各种医疗废物的分配及运输、处理技术的匹配和网络节点的处理能力等决策问题。考虑到疫情期间危险医疗废物的高传染性,本文以总成本和总风险最小化为目标构建了多目标混合整数规划模型,同时考虑了现实情况中网络节点处理能力有限、危险医疗废物种类和相应处理技术匹配等约束。本文构建的模型在处理危险医疗废物管理问题方面更具有一般性。此外,不同于大多数文献采用加权求和方法和启发式方法求解多目标优化问题,本文同时采用了另外两种方法:增广加权契比雪夫法和增广ε约束方法。最后,将本文模型应用到实例中并计算求解,即中国武汉新冠肺炎疫情期间危险医疗废物管理系统网络设计问题。数值实验结果表明增广ε约束方法的数值表现优于其他两种方法。合理地设计危险医疗废物管理系统网络能够有效地平衡总经济成本和总风险。决策者通过调节权重因子、网络节点处理能力比率和回收率等因素控制医疗废物管理系统的总经济成本和总风险;同时决策者可以根据疫情发展情况灵活调整目标函数权重,获得相应的医疗废物处理方案,进而实现决策目标。

本文尚存在一些不足,未来可以更深入的研究。首先,本文的采用的算法在求解大规模现实问题时耗时较长,存在优化的空间,以使问题在较短时间内被解决。此外,现实情况下疫情的发展具有很大不确定性,比如感染人数的变化不确定等,利用模型如何更加准确地刻画这些不确定性是值得探讨的问题。