基于典型机器学习算法的航空发动机价格估算模型研究

刘子源, 张大维, 高 星

(中国人民解放军92228部队, 北京 100072)

0 引 言

航空发动机的研制是一项周期长、难度大、风险高的系统工程，经常面临着拖进度、降指标、涨价格的困境[1]。例如，美国的F-135发动机，其实际价格已超过设定基准的30%以上[2]，给经济可承受性带来了严峻挑战。本文以涡轴、涡桨发动机为研究对象，运用多种方法，通过训练和评估，构建发动机订购价格估算模型，对装备寿命周期费用的评估和发展决策具有重要意义。

1 研究现状

当前，装备价格估算方法主要包括参数法、专家法、工程法等[3]。其中，参数法具有适用范围广、可以量化分析等优势，得到了广泛应用，其本质是寻找装备特征与价格的映射关系，通过数据分析得到估算模型，进而预测新装备价格。

航空发动机的费用分析具有重要意义，近年来多位学者对此进行了大量研究。文献[2,4]分别基于小样本理论、偏最小二乘方法，建立了航空发动机研制费估算模型；文献[5]基于线性回归方法，估算了我国航空涡扇发动机的新研成本与改进成本。以上工作对航空发动机的价格估算起到了良好促进和发展作用，但研究对象大多集中在研制费用，估算方法大多以线性回归为主，没有评估不同模型的效果。

由于航空发动机的订购批量大、单价高，因此订购费用在寿命周期费用中占据更大比例。同时，随着机器学习等数据科学的不断发展，很多新方法应用于各行业的估算工作中，如运用AdaBoost方法对直升机制造复杂度进行估算[6]、运用随机森林方法对水稻产量进行估算[7]、运用决策树算法对药品进行成本-效果分析[8]等，均取得了较好效果，为装备价格估算带来了新的思路。因此，本文针对涡轴、涡桨发动机，运用决策树、KNN、AdaBoost、随机森林等多种机器学习算法，建立估算模型，为订购价格论证提供支撑手段。

2 主要特征及数据收集

航空发动机的价格估算需要基于发动机特点，筛选影响因素，运用相关算法进行估算模型的研究和分析。

2.1 主要参数筛选

航空发动机主要包括涡扇、涡喷、涡轴、涡桨、活塞等类型，不同类型发动机的工作方式、性能指标不同，需要分类分析。不同于涡扇、涡喷发动机主要通过向后喷射高速燃气获得向前的推力，涡轴、涡桨发动机主要通过输出轴功率带动旋翼(涡轴发动机)或螺旋桨(涡桨发动机)获得动力，因此二者具有很高相似度。很多涡轴、涡桨发动机都是基于同一基础发展而来，如PT6A涡桨发动机和PT6B涡轴发动机都是PT6系列发动机中的衍生型。因此，虽然建立价格估算模型的方法适用于所有种类航空发动机，但以涡轴、涡桨发动机为例进行分析，有利于扩充数据范围，增加样本容量，提升模型估算科学性。

涡轴、涡桨发动机主要特征参数如下：起飞功率是起飞状态下可以输出的功率，是衡量发动机做功能力最主要的指标；耗油率是单位时间输出单位功率消耗的燃油量，是经济性指标，数值越小经济性越好；功重比是功率与干质量比值，越大表示性能越好；空气流量是单位时间流过发动机的空气质量，是重要的设计参数；总增压比衡量对空气的压缩程度，与发动机效率有很密切关系；长度描述发动机的物理尺寸[9]。

2.2 数据收集与处理

查阅有关资料[10]，得到国际上部分涡轴、涡桨发动机相关参数。由于存在不完整、不一致的脏数据，导致无法直接建立模型或建模效果不理想，因此需进行预处理，主要包括数据清洗和数据集成两方面。

(1)数据清洗

针对样本数据，数据清洗主要包括：1)对于价格数据，统一折算至2020年的“万美元”，便于在统一货币基准下建模分析；2)对于价格数据涉及多个型号的，暂取平均值； 3)如果某数值给出的是范围，取最大值与最小值的平均值；4)由于样本数量有限，为避免填充数据对模型准确性的影响，不进行数据填充。若某关键特征数据缺失，则剔除该样本。

(2)数据集成

针对样本数据，数据集成主要包括：1)功率、耗油率取不同状态功率、耗油率的最大值；2)功重比、空气流量、总增压比、长度取原值。预处理后，得到的样本数据如表1所示。表1中，Y表示发动机订购价格；X1表示起飞功率；X2表示耗油率；X3表示功重比；X4表示空气流量；X5表示总增压比；X6表示长度。

2.3 训练集与测试集

为便于模型建立，选定第4、15、20、29、30、34等6个样本作为测试集，用于模型测试和评估；剩余29个样本作为训练集，用于模型训练和分析。

3 估算模型的建立与评估

模型建立主要包括以下四个环节：1)进行相关性分析，观察变量间相关性；2)运用训练集样本，基于不同算法构建费用估算模型；3)对测试集样本预测，评估泛化能力；4)性能比较，并结合可实现性、易用性等方面综合评估，推荐实际工作中应用的模型。

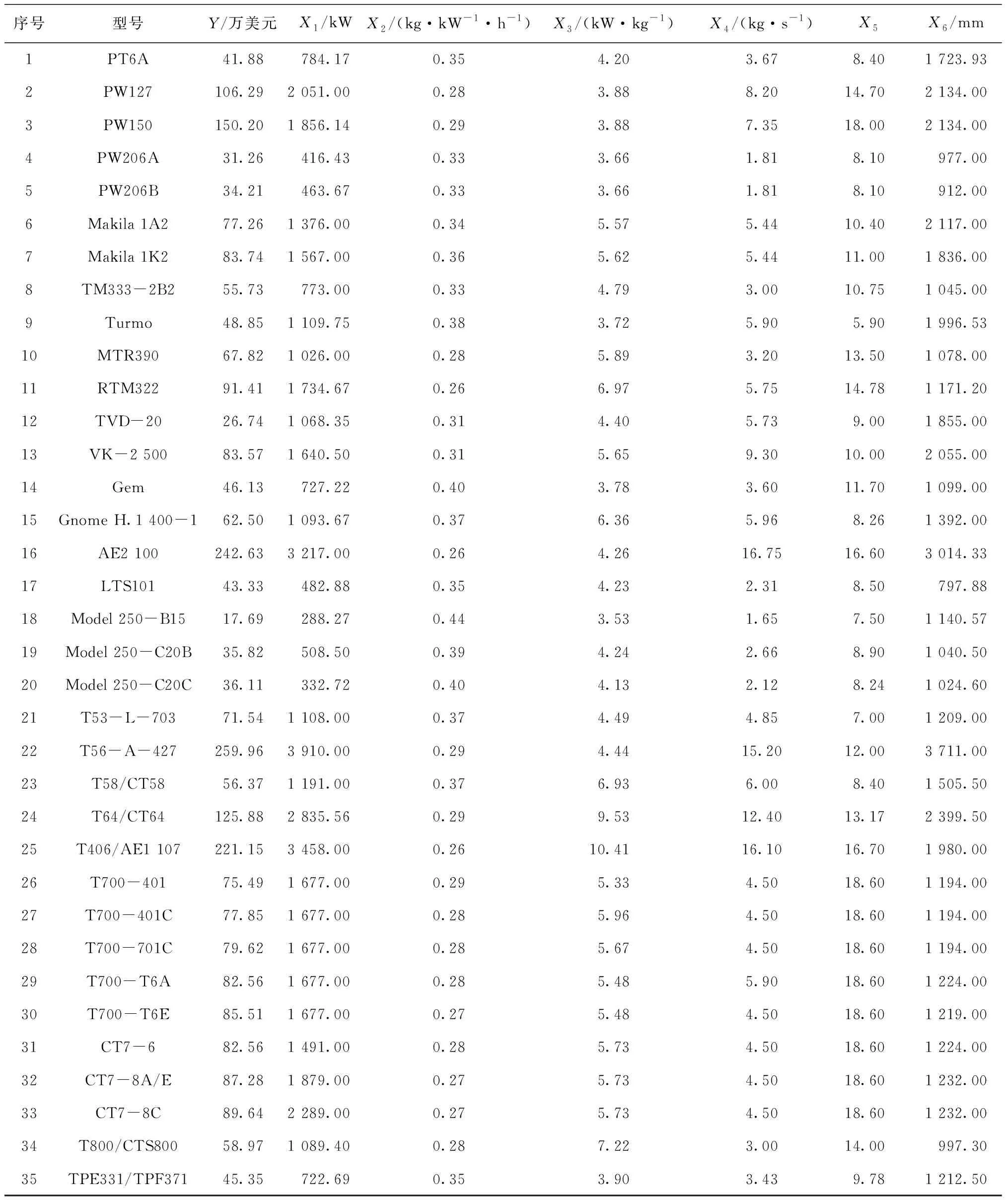
表1 部分国际涡轴、涡桨发动机主要参数及价格数据[10]

3.1 相关性分析

相关性可通过计算变量间的Pearson相关系数r进行分析，一般而言，相关系数绝对值越大，相关性越强。具体可分为：极强相关(0.8≤r≤1)、强相关(0.6≤r<0.8)、中等程度相关(0.4≤r<0.6)、弱相关(0.2≤r<0.4)、极弱相关或无相关(0≤r<0.2)。样本变量间相关系数，如表2所示。

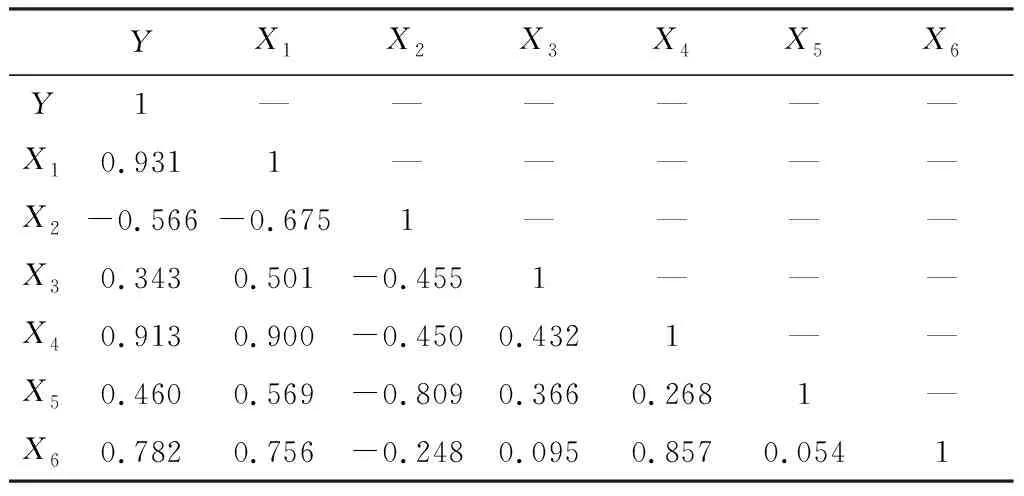
表2 样本特征相关系数

首先，观察各变量与价格Y的相关性：X1、X4与Y具有极强相关性，X6与Y具有强相关性，X2、X5与Y具有中等程度相关性。

其次，观察不同自变量间的相关性：X1与X4、X2与X5、X4与X6具有极强相关性，X1与X6具有强相关性。

综上，应优先考虑起飞功率X1、空气流量X4及长度X6等作为费用驱动因子；起飞功率X1与空气流量X4、耗油率X2与总增压比X5、空气流量X4与长度X6高度相关，在线性回归中要考虑多重共线性带来的影响。

3.2 模型训练与评估

3.2.1单变量建模分析

单变量的优势是相对简单，信息要求低，可以抓住关键因素，便于概念设计时使用。根据相关性分析结果，选择起飞功率作为自变量，分别运用多项式、乘幂、指数等方法建立估算模型，其拟合曲线如图1所示。

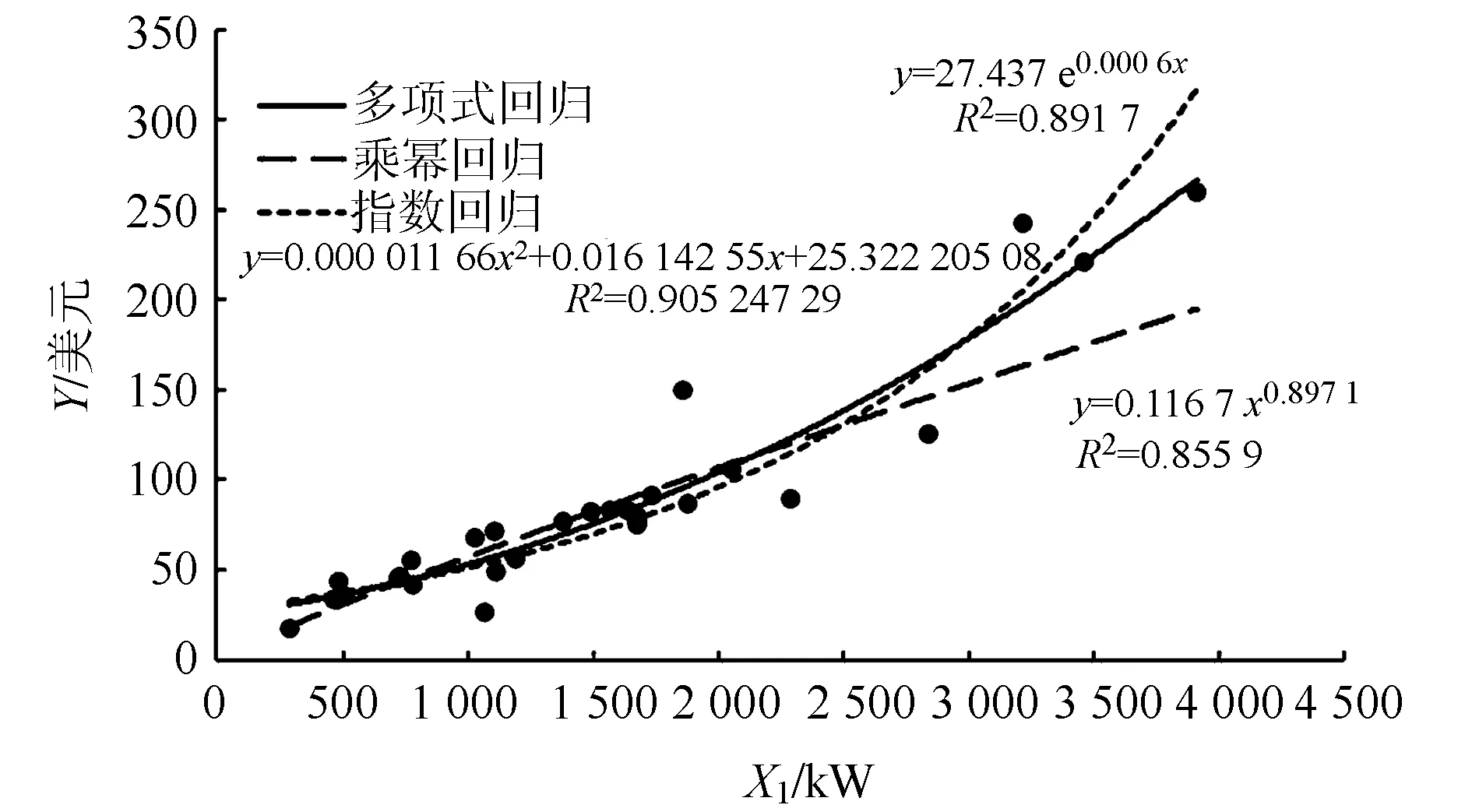
图1 单因子回归拟合曲线

可以看出，三种模型对训练样本的拟合情况较为接近，多项式回归(二次多项式)的R2=90.52%，乘幂回归的R2=85.59%，指数回归的R2=89.17%，多项式回归拟合程度最高，对样本变异的解释最好，同时表达简单、易于使用。这里以二次多项式模型作为单因子回归模型，其表达式为

25.322 205 08

(1)

运用模型对测试集样本预测，结果如表3所示。

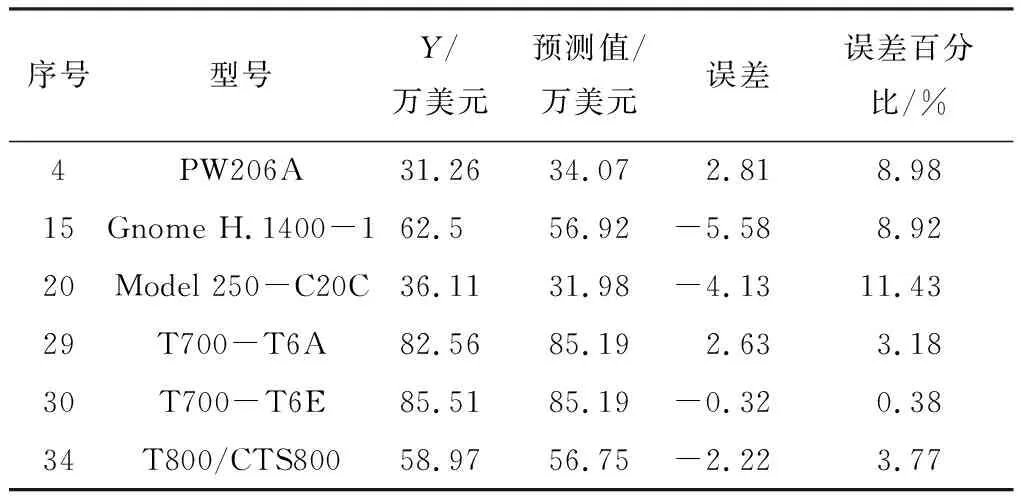
表3 二次多项式模型测试集预测结果

由表3可以得到，预测误差最大值为11.43%、最小值为0.38%、误差平均值平均值为6.11%，拟合优度R2为90.52%。整体预测准确性较高、稳定性较好。

3.2.2偏最小二乘回归分析

通过相关性分析可以看出，不同特征间存在较强的相关性。这里运用偏最小二乘法，牺牲部分无偏性，解决多重共线性问题。通过训练得到偏最小二乘估算模型，对测试集预测，结果如表4所示。

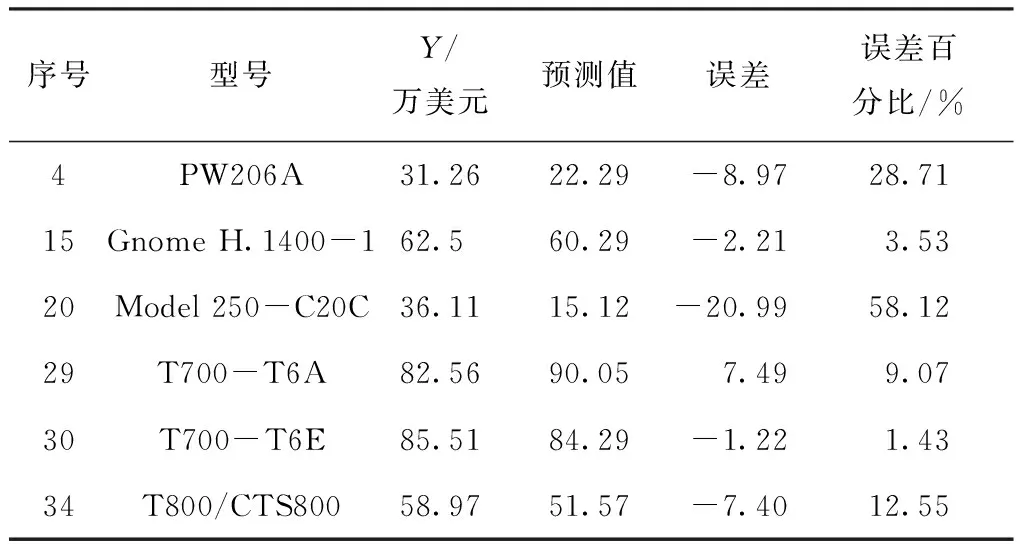
表4 偏最小二乘模型测试集预测结果

可以看出，模型的拟合优度R2=88.76%，对样本变异有较好的解释。模型预测误差最大值为58.12%、最小值为1.43%、平均值为18.90%。虽然解决了变量多重共线性问题，但由于样本特征、数据特点，该方法对研究问题的适用性不强，整体预测准确性较低、稳定性较差。

3.2.3决策树建模分析

决策树是一种对实例进行分类和回归的树形结构，由结点和有向边组成，其中结点包含内部结点和叶结点两种。内部结点表示一个特征或属性，叶结点表示一个类。当决策树用于回归时，基于平方误差最小化准则进行特征选择，生成二叉树[11]。

为充分利用样本信息并避免偶然训练造成的误差，这里将样本的所有特征作为自变量，将训练集进一步划分为内部训练集和验证集组合，并进行10折交叉验证。使用网格搜索的方式选取最优参数，提高样本的利用程度。运用Python并调用Scikit-learn库，可以训练得到决策树模型。运用建立好的决策树估算模型对测试集样本预测，结果如表5所示。

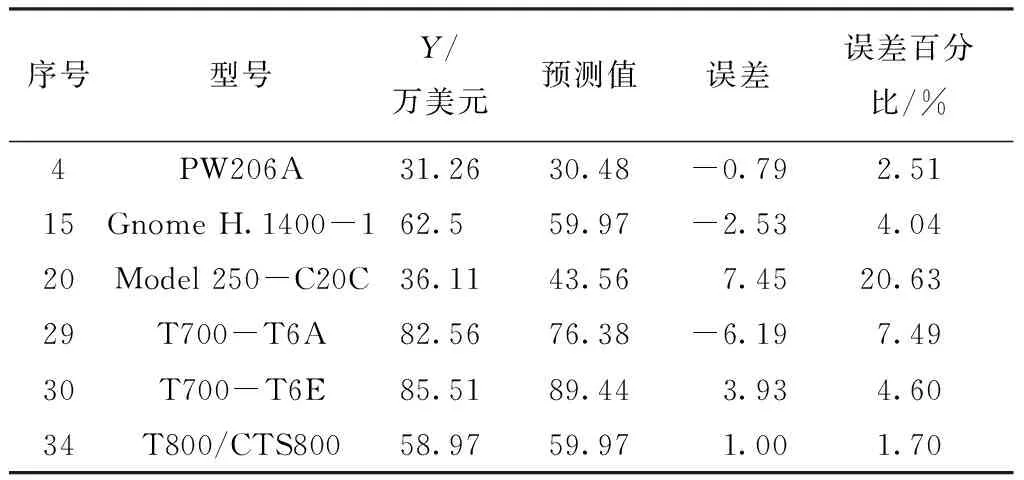
表5 决策树模型测试集预测结果

可以看出，模型训练的拟合优度R2=98.09%，对样本变异具有很好的解释能力，预测误差的最大值为20.63%、最小值为1.70%、平均值为6.83%，预测效果具有一定波动性，整体准确性较高。

3.2.4KNN建模分析

KNN的基本原理是给定一个训练数据集，对新的输入样本，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把输入样本归为该类。在进行回归问题分析时，样本对应的输出值，就通过这k个实例的值来确定。KNN算法具有简单、直观、准确性高、对异常值和噪声容忍度较高等优点，但同时也有计算量和内存消耗量较大的缺点[11]。

运用KNN算法，采用与决策树相同的方式，建立回归模型。运用建立的KNN模型对测试集样本进行预测分析，结果如表6所示。

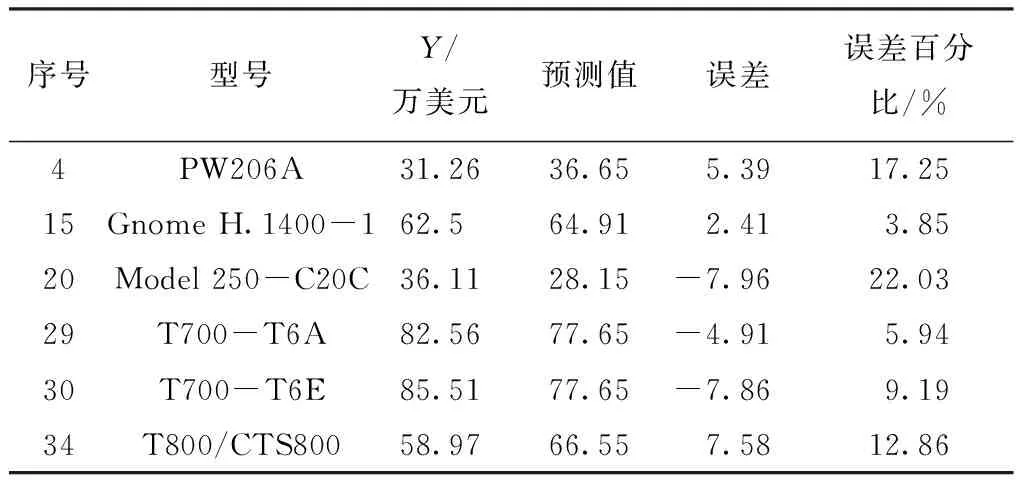
表6 KNN模型测试集预测结果

可以看出，模型拟合优度R2约为100%，可以对样本变异进行近乎全部解释，模型预测误差的最大值为22.03%、最小值为3.85%、平均值为11.86%。模型虽然整体拟合能力强，但预测误差较大，不利于经费估算工作。

3.2.5AdaBoost建模分析

AdaBoost是Boosting算法的一种。Boosting算法也称为增强学习或提升法，是一族可以将弱学习器提升为强学习器的算法。其原理是：先从训练样本中训练出一个弱学习器，再根据弱学习器的表现调整样本分布，使在先前弱学习器中表现不好的样本在后续训练中受到更多关注，以此训练下一个弱学习器。不断重复上述步骤，直到训练出所有弱学习器，再将弱学习器组合为强学习器[12]。采用与决策树相同的方式，训练获得AdaBoost估算模型，对测试集样本进行预测分析，结果如表7所示。

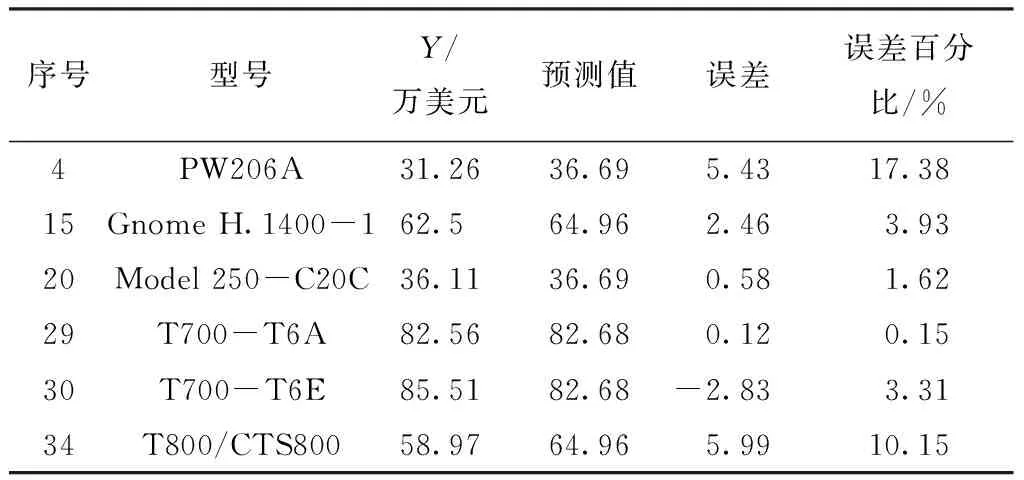
表7 AdaBoost模型测试集预测结果

可以看出，模型训练拟合优度R2=98.81%，对样本变异解释较好。模型预测误差最大值为17.38%、最小值为0.15%、平均值为6.09%，模型不仅具有较好的解释能力，且预测准确性较高。

3.2.6随机森林建模分析

随机森林是一种应用十分广泛的机器学习算法，是通过集成学习的思想将多颗树集成的算法，其基本单元是决策树，本质是集成学习。随机森林算法具有灵活实用、准确率高、能处理高维特征输入样本、对缺省值问题也能够获得很好的结果等优点，但也存在运算速度慢、可能由于有很多相似决策树而掩盖真实结果等缺点，但综合而言，随机森林仍是一种效率很高、具有很好泛化能力的算法[13]。同上文，可以训练获得随机森林估算模型，运用建立好的模型对测试集样本进行预测分析，结果如表8所示。

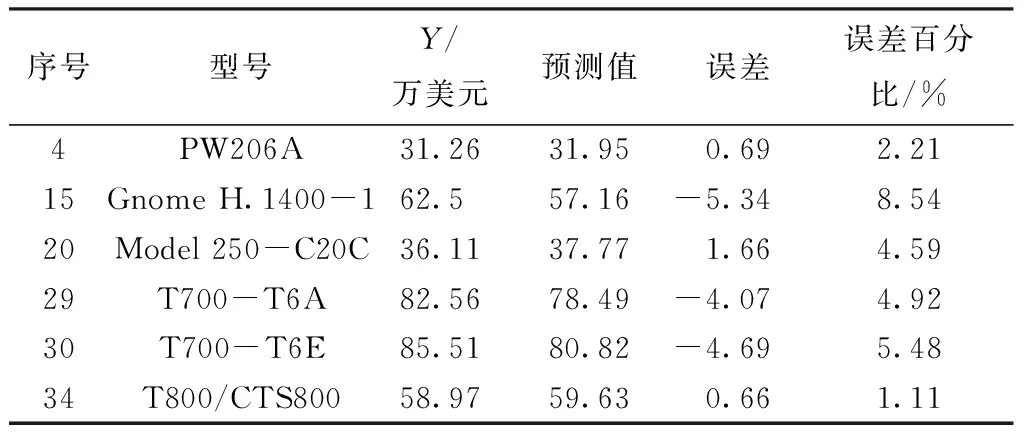
表8 随机森林模型测试集预测结果

可以看出，模型拟合优度R2=97.42%，解释能力较强，模型预测误差的最大值为8.54%、最小值为1.11%、平均值为4.48%。总体而言，模型预测准确性很高且表现较为稳定。

3.3 模型性能比较与选择

分别运用以上几种模型对全体样本进行预测，得到拟合值与真实值的散点图如图2所示。

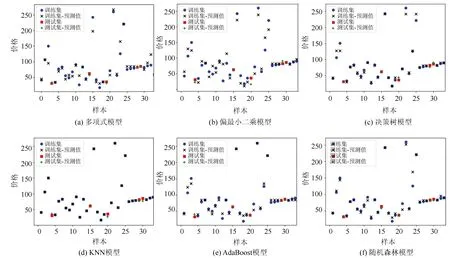
图2 各模型拟合预测结果

通过多个方面对模型进行比较和分析，可以评价不同模型的优缺点，进而为实际工作中的模型选择提供依据和参考。

可以看出，各模型对测试集样本的预测能力各不相同，一方面与模型的泛化能力有关，一方面也与样本特征有关。例如，测试集中的Model 250-C20C是贝尔OH-58C临时侦察直升机计划的生产型发动机，批量较小，因此其价格发生规律与其他发动机有一定差别，各模型对该样本的预测结果差异较大。

在对模型整体表现评估时，选用拟合优度R2评估模型的拟合效果和解释能力，选用预测平均误差评估模型的预测准确性和泛化能力，选用预测误差方差评估泛化稳定性，通过输入参数的可获得性与使用便捷性评估模型的易用性。几种模型的比较结果如表9所示。

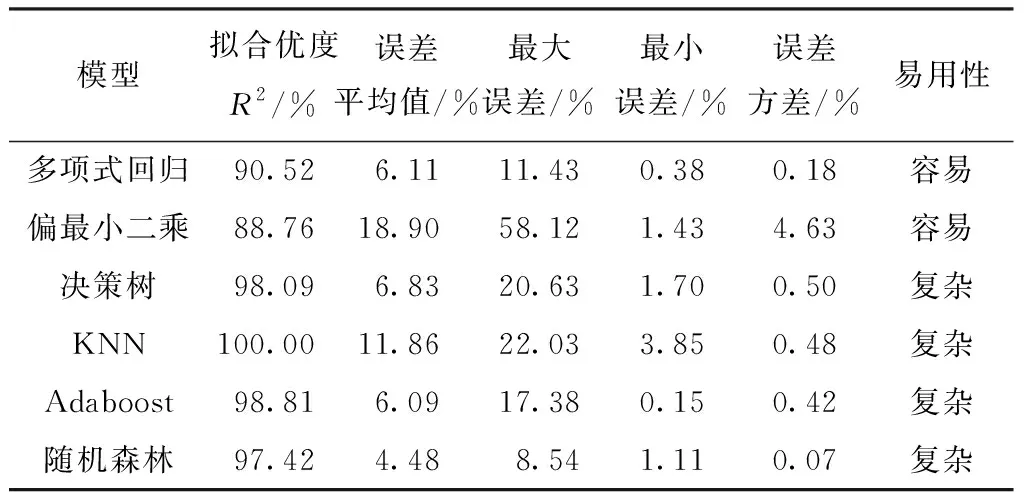
表9 几种估算模型性能比较

结合图2与表9，可以从以下四个方面来评价模型。

1)从对变异的解释能力看，KNN模型的R2达到了100%，具有极强的解释能力；决策树、AdaBoost、随机森林等3种模型的R2也达到了97%～99%，同样具有很强的解释能力。多项式回归、偏最小二乘两种模型的解释能力虽不如其他几种方法，但也达到约90%，变异解释效果较好。

2)从预测准确性看，多项式回归、决策树、AdaBoost及随机森林等4种方法的预测误差平均值均在10%以内，满足了论证阶段对涡轴、涡桨发动机价格估算的要求。其中，随机森林模型的预测误差平均值是所有模型中最小的，在5%以内(4.48%)；KNN模型的预测误差平均值为11.86%，与其他几种方法相比仍有差距；偏最小二乘法的预测误差平均值约18.90%，误差较大，不建议应用。

3)从预测稳定性来看，除偏最小二乘模型外，其余模型的预测误差方差均在0.5%以内，具有较好的预测稳定性。其中，稳定性最好是随机森林模型，误差的最大值和最小值均在10%以内，误差的方差仅为0.07%，具有很好的稳定性。

4)从易用性角度看，多项式回归模型仅需要功率参数就可以使用，一般在目标图像阶段就可以获得；模型表达式可以显式写出，使用起来较为便捷。决策树、KNN、AdaBoost、随机森林等几种模型所需参数较多，但这些参数一般在论证阶段也可以获得；模型无法显式表达，使用时需要专用工具，具有一定复杂性。

综上，随机森林在解释能力、预测准确性和预测稳定性等方面都有着十分优秀的表现，是综合效果很好的价格估算模型。多项式模型在各个方面有着较为均衡的表现，且使用便捷，同样较为合适。

因此，建议以随机森林和多项式回归模型作为涡轴、涡桨发动机的价格估算模型，根据可获得的信息和实际要求选择运用。若可获得信息较少，仅有功率信息，使用多项式模型；若可获得其他信息，则使用随机森林模型。

4 结 语

通过本文的研究，获得以下三点结论。

1)涡轴、涡桨发动机的价格包含多种影响因素，其中相关性最强的是功率，通过功率参数就可以获得效果较好的价格估算模型。

2)建立了多种涡轴、涡桨发动机价格估算模型，其中多项式模型、随机森林模型、AdaBoost模型、决策树模型都可以对价格进行很好的估算，预测精度在10%以内甚至5%以内，可以满足论证阶段对发动机价格的估算要求，支撑装备型号论证工作。

3)随机森林模型和多项式模型是最适合涡轴、涡桨发动机价格估算的模型，两种方法具有各自的优势和特点，需要结合具体情况选择使用。

同时，在数据进一步丰富、样本更加全面的情况下，未来可将上述模型调整完善，用于涡扇、涡喷发动机以及国产(军用)航空发动机的订购价格估算，为我国航空发动机的发展论证奠定基础，提供更加丰富的手段工具支撑。