热循环下集成电路板疲劳寿命预测

徐鹏博， 吕卫民， 李永强， 刘陵顺

(海军航空大学， 山东 烟台 264001)

0 引 言

随着计算机技术和微电子信息技术的不断进步，电子元件一直在向着微型化方向发展。封装技术的水平决定了电子产品的发展趋势与工作寿命。集成电路板上的电子元件数量在增多，元件和焊点的尺寸在不断缩小，这对于工艺制造水平要求极高。每一块集成电路板上都含有成百上千个焊点。而焊点作为媒介将封装芯片与印制电路板(Printed Circuit Board, PCB)连接起来，既承担了电力连接的任务，使得电路元件和电子元件之间可以传递电信号，又承担了机械连接的任务，可以发挥缓冲应力的作用，将封装芯片固定在PCB板上使其无法脱落，还提供了空间使封装芯片形成散热通路，在一定程度上减轻了热量对电子元件的影响。一旦焊点出现问题，势必会造成电路板上的其他组件无法正常工作。因此，焊点也成为了电子元件中的重点关注对象[1-2]。

集成电路板工作环境的调查研究显示：50%的故障由温度引起的，20%的故障由振动冲击导致的，其余导致故障的环境因素则是盐碱湿度、灰尘、冲击、低气压等[3]。因此，重点研究温度对电子元器件可靠性的影响十分必要。近年来，国内外学者对此进行了大量的研究。文献[4]针对塑料焊球阵列封装(Plastic Ball Grid Array Package, PBGA)进行建模，利用有限元软件加载了五种不同的热循环条件，通过比对计算结果发现高温加载时间维持得越长，塑性应变累积得越多，焊点更易破坏；而热循环过程中温度的变化幅值也是焊点疲劳失效的一个重要原因。文献[5]对球栅阵列封装(Ball Grid Array Package, BGA)焊点进行了大量的热循环实验，通过纳米压痕技术获取焊料杨氏模量、硬度、蠕变等机械性能，发现经过几百次热循环后，焊料杨氏模量和硬度会显著下降，蠕变应变率激增的结论。文献[6]以PBGA封装芯片作为分析对象，根据其服役环境建立任务时间谱，对芯片采取了热电耦合分析，针对芯片退化现象和焊点热疲劳失效采取了Arrhenius模型和Coffin-Manson疲劳寿命模型对封装芯片进行预测，为相关类型的电子封装元件在环境适应性和热力学仿真等方面拓宽了研究思路。

集成电路板在经历热循环加载时，由于电子元件种类多，各个部分的材质不尽相同。材料的热膨胀系数(Coefficient of Thermal Expansion, CTE)严重失配，在受到周期性应力的过程中焊点内部会持续累积应变能，从而形成了焊点从萌生裂纹到裂纹扩展最后失效的过程，封装芯片和电路板也会因温度升高出现热膨胀和翘曲现象[7]。本文以车载导航计算机中的集成电路板作为研究对象，利用有限元软件对集成电路板进行热-结构分析，并计算出热疲劳寿命。

1 电路板有限元模型的建立

1.1 有限元模型的简化

选取的集成电路板上安装有诸多不同类型的电子元件，其中包含模块电源、低压差稳压器、贴片电阻、电解电容等。在对其进行建模时，应在保证计算结果准确的前提下，对模型做出合理假设并进行适当简化[8]。

1)忽略封装结构内部电路影响，将电路板上的电子元件看作是由焊点、引脚、塑封材料、基板组成，各个部分看作是理想连接。将焊点定义为粘塑性材料，其余看作是线性材料。

2)重点关注焊点数目多的电子元件，假设焊点内部均匀分布，无空洞缺陷。忽略一些微小电子元件，将模块电源等大型元件简化成等效质量块。

3)为确保网格的精准划分，将电路板两侧接口用等效的约束替代，并对电路板不规则之处进行简化处理。

因为电路板上元件布局复杂，并考虑到后续热传导和热对流对电子元件的影响，选择SOLIDWORKS软件进行实物建模，建模过程中采取的是自底向顶的设计思路。首先建立焊点、引脚、塑封体这几种单元体，将它们装配在一起形成一个个电子元件，最后安放在PCB板上。集成电路板以及局部电子元件如图1、图2所示，建立完的模型包含7种电子元件，共由661个部件组成。

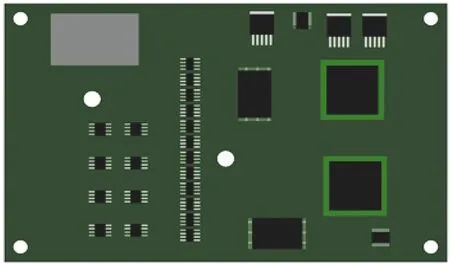
图1 集成电路板三维模型

图2 电子元件三维模型

1.2 材料属性

事实上，电子元件由多种材料组成，如果将每种结构的材料都完全还原，势必会加大运算量，导致结果不易收敛。因此在添加材料属性时，对电子元件材料属性相近的结构进行近似处理，简化后共涉及5种材料。除焊点材料外，其余材料视作均为各向同性线弹性材料且设置为固定值[9]。相关材料参数如表1、表2所示。

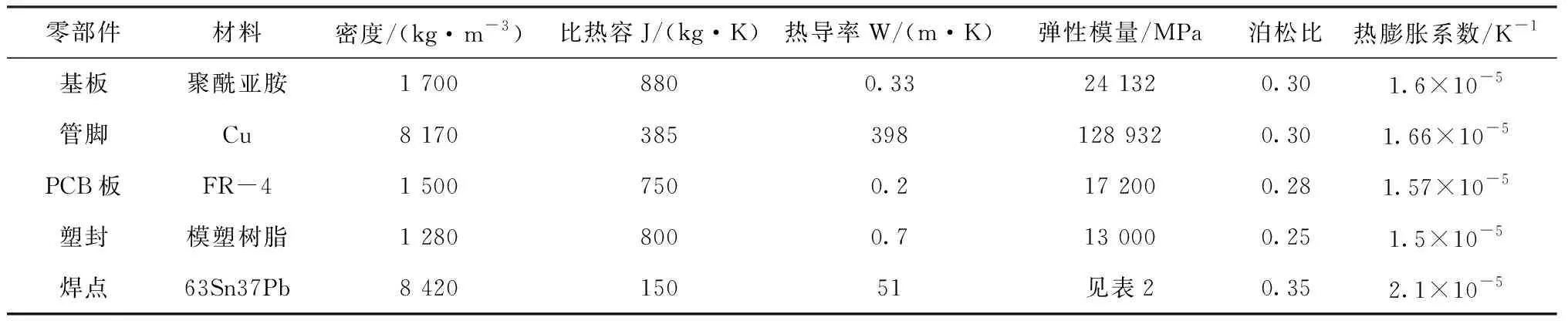
表1 各组成部分的材料参数

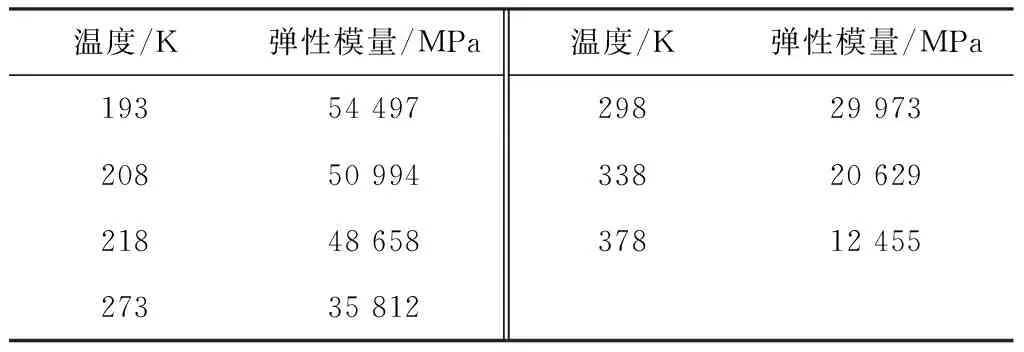
表2 63SnPb37弹性模量随温度变化情况

集成电路板在热循环加载的过程中，焊点会产生塑性变形和蠕变变形。这种与温度、时间相关联的非弹性行为，可以应用Anand本构方程来处理[10]。Anand模型运用单一独立的内部变量来描述高温环境下金属材料的力学行为，它将高温导致的硬化行为考虑进去，并将粘塑性这种被环境温度、应变速率所影响的特殊材料性质进一步解释说明。Anand本构方程为

(1)

式中：εP为非弹性应变速率；A为常数；ξ为应力乘子；Q为激活能量；T为绝对温度；R为普通气体常数；m为应变速率敏感指数；s为阻抗因子；h为应变硬化参数；sinh为双曲正弦；σ为有效应力。

硬化参数h的表达方程为

(2)

其中，

(3)

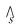
内变量演化方程为

(4)

(5)

式中：S0为初始形变阻抗

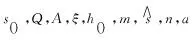
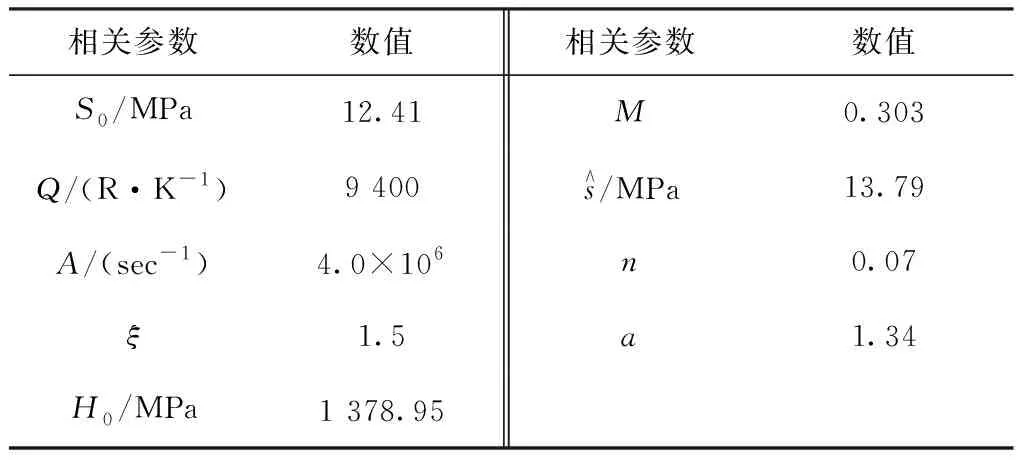
表3 63Sn37Pb焊料的Anand本构模型参数

1.3 有限元网格划分

在对电路板进行网格划分时，对PCB板采取扫掠划分法，对电子元件采用自动划分方式。为了保证解算速率和结果精度，将焊点的网格单元尺寸设置为0.15 mm，PCB板网格单元尺寸设置为2 mm，并对部分焊点进行细化处理，提高网格质量。集成电路板的网格划分情况如图3所示。

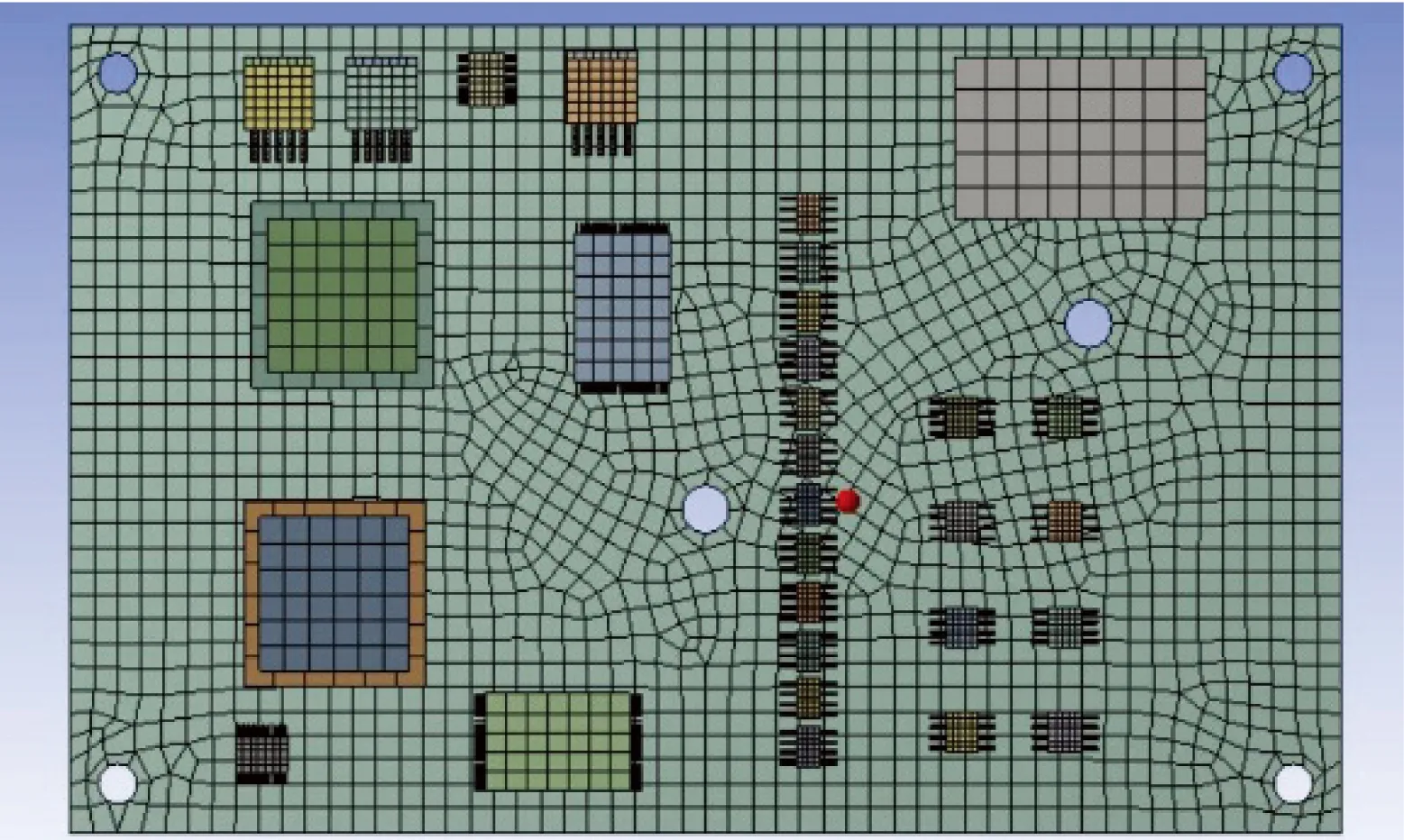
图3 有限元网格划分结果

2 有限元仿真分析

2.1 热循环加载与求解

施加在集成电路板上的热循环载荷是以美军相关测试标准和电路板实际的工作环境温度作为参考依据，最终确定热循环范围为-55～125 ℃。一次热循环共包含五个载荷步，分为三个升降温环节和两个保温环节，起始温度为25 ℃。温度变化速率设置为30 ℃/min，每次保温时长为15 min，最大变温时长为6 min，一个热循环时长为42 min[11]。

将SOLIDWORKS软件中的模型导入到Ansys中，首先建立瞬态热分析模块，导入热循环载荷。热循环载荷设置如图4所示，设置10个热循环周期，总时长为25 200 s，在每个载荷步下设置10个子载荷步，共计500个子步。将热循环载荷施加到电子元件和PCB板表面，之后将电路板温度场导入到瞬态结构分析模块，并依据电路板工作环境对PCB板的部分表面以及四个孔洞内表面施加固定约束。

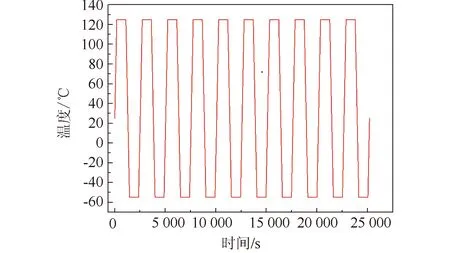
图4 热循环加载情况

2.2 有限元结果分析

如图5所示，从焊点的等效塑性应变云图中可以得出在热循环载荷下集成电路板上最危险位置是右下角电子元件LVC244A的焊点。这是因为当加载温度开始发生变化时，不论是升温环节还是降温环节，由于电路板上各处温度并不完全相同，电路板四周又被施加了固定约束，在热-结构耦合作用下，电路板整体向上凸起，电路板边缘处的电子元件受到的应力应变要高于其他电子元件[12]。焊点的最大等效塑性应变出现在焊点与PCB板连接面的边缘位置。

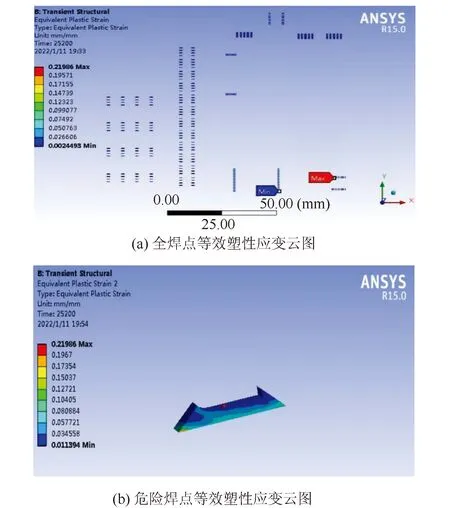
图5 焊点的等效塑性应变云图

图6为危险焊点的应力变化曲线，分析该曲线可以发现焊点在热循环加载下，其内部出现了周期性应力。通过分析应力变化趋势和对应的热循环加载环节，应力从第六个热循环周期开始趋于稳定，在升温环节中应力下降，在降温环节中应力升高。最大等效应力出现在-55 ℃保温环节，最小等效应力出现在125 ℃保温环节。

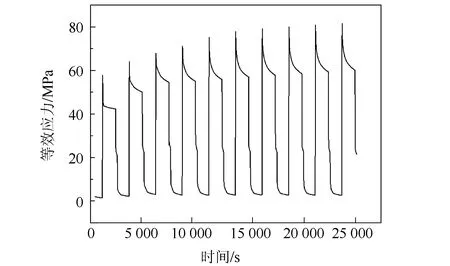
图6 危险焊点应力曲线图

2.3 疲劳寿命预测

由仿真结果可知：集成电路板的热疲劳寿命是由危险焊点决定的。电路板上的焊点在周期性热应力循环作用下疲劳失效。解决此类疲劳失效问题需要借助寿命预测模型。根据不同的力学参量，疲劳寿命预测模型可分为塑性变形疲劳预测模型、蠕变变形疲劳预测模型、断裂参量疲劳预测模型和能量疲劳预测模型[13]。其中塑性变形疲劳寿命预测模型以塑性变形量作为研究对象，塑性变形具有与时间无正相关关系的特性，将剪切变量和相关系数代入相对应的公式中可得到元件最终失效所经历的周期循环次数。此类模型应用广泛，结果较为准确。典型的塑性变形预测模型有Manson-Coffin模型、Ostergren模型、Miller模型。

计算焊点热疲劳寿命选取了Manson-Coffin模型，该模型最早是由Manson提出的，该模型阐明了应力和疲劳寿命之间的关系，并可以通过热循环加载下产生的塑性应变来确定构件疲劳寿命。Coffin总结了裂纹产生的规律，分别对室温和高温情况下低周期和高周期循环产生的疲劳损伤结果进行分析。解释了循环应变、工作环境、波形效应和塑性不稳定性等因素对构件的影响。Engelmaier考虑到了热循环过程中温度的变化和频率，并对模型做出了改进。

改进后的Manson-Coffin模型如下[14]：

(6)

其中，

c=-0.442-6×10-4Tm+1.74×10-2ln(1+f)

(7)

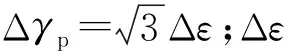
图7等效塑性变形曲线图显示：随着热循环周期数目增加，等效塑性变形增量逐渐稳定。将第十个循环周期选为目标时间段，εpmax和εpmin分别代表该段时间内等效塑性变形的最大值和最小值，Δε=εpmax-εpmin=0.219 86-0.208 17=0.011 69。经过计算可得到危险焊点的热疲劳寿命为2 857.1个循环周期。

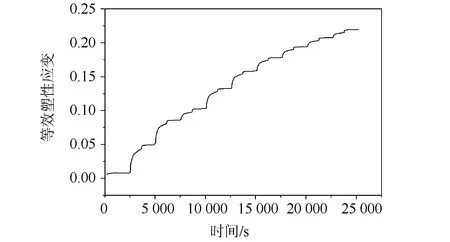
图7 危险焊点等效塑性变形曲线图

图8为焊点内部的等效应力与等效应变构成的迟滞环。以能量作为参考的疲劳寿命预测模型是将电子元件和焊点内部应力应变引发的迟滞效应作为研究基础，温度载荷每一次循环都会产生相对应的应变能。当应变能累积到一定程度就会引发元件断裂致使其失效。这一模型利用能量与疲劳推导出经验公式。典型的模型有：Akay模型和Darveaux模型。

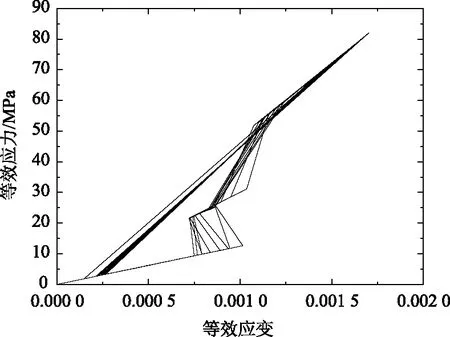
图8 等效应力应变迟滞环

基于能量的Darveaux模型通过提取热循环周期中焊点内部的应变能及应变能密度来计算疲劳寿命。并且该模型引入了裂纹扩展速率和断裂临近长度等参量来描述疲劳寿命[15]。

N0=K1(ΔWave)k2

(8)

(9)

(10)

式中：k1、k2、k3、k4是与材料疲劳失效有关的裂纹扩展系数，如表4所示；Nf为材料失效破坏时所经历的热循环周期数；N0为材料刚开始出现裂纹时经历的热循环周期数；a为材料发生断裂时的长度；da/dN为裂纹扩展的速率；ΔWave为稳定的体积平均应变能密度增量。

表4 Darveaux模型裂纹扩展系数

由于焊点的粘塑性应变能及其密度与Ansys网格划分的质量和大小等方面有关，为了尽可能减少因网格划分对最终结果的影响，采用体积加权法计算平均应变能密度Wave[16]。

(11)

式中：i为焊点上各单元体的序列号；vi为焊点上第i个单元体对应的体积；Wi为焊点上第i个单元体对应的粘塑性应变能密度；N为焊点上的单元体总数；Wave1和Wave2分别对应着某个热循环周期起始时刻和结束时刻的平均应变能密度。

在利用该模型进行计算时需注意：体积平均应变能增量和材料断裂时裂纹长度应采用英制单位，因此需要将这两个参数分别除以6.894 757e-3和25.4。根据Ansys软件后处理器得到ΔWave=0.067 48 MPa=9.786 6 Psi,危险焊点的热疲劳寿命为2 987.61个循环周期。

2.4 无铅焊料的讨论

随着现代电子制造工艺的迅速发展，目前无铅焊料的应用越来越多。为了提高电路板热疲劳寿命，可以对焊料类型进行研究，将传统的锡铅焊点与新型无铅焊点进行对比分析。新型焊点材料则选用SAC305合金，这种无铅合金是由96.5%的锡、3%的银和0.5%的铜组成，具有低成本、良好的耐疲劳性、兼容各种类型的阻焊剂等特点。查阅文献[17]，将SAC305焊料的热特性参数和Anand本构方程参数输入到Workbench材料库中。

经过计算后，63Sn37Pb和SAC305焊点的热疲劳寿命如表5所示。通过分析比对后发现：采用基于塑性变形疲劳预测模型和基于能量疲劳预测模型得到结果十分接近，并且SAC305焊点的热疲劳寿命要远高于63Sn37Pb焊点。文献[18]采用基于蠕变应变和蠕变应变能密度两种方法计算焊点热疲劳寿命，文献[19]对CBGA焊点在极限温度-150～180 ℃条件下的可靠性进行研究，二者都证明了SAC305焊点的可靠性要高于63Sn37Pb。因此，从电路板热疲劳寿命角度考虑，可以选择使用SAC305焊料制作焊点，这也为电子元器件可靠性研究提供了参考。

表5 不同焊点热疲劳寿命预测

3 结 语

1)基于Anand粘塑方程对某型集成电路板进行有限元模拟，并对电路板各电子元件进行了一些合理的假设简化。有限元计算结果表明集成电路板右下角的LVC244A电子元件上的焊点受到的应力应变最大。焊点在热循环加载下，其内部出现了周期性应力。通过分析应力变化趋势和对应的热循环加载环节，发现应力从第六个热循环周期开始趋于稳定，在升温环节中应力下降，在降温环节应力升高。电路板及板上的电子元件在热循环过程中发生较大变形。

2)使用Manson-Coffin和Darveaux两个疲劳寿命预测模型进行计算，结果显示SAC305焊点热疲劳寿命高于63Sn37Pb焊点。证明SAC305可以代替63Sn37Pb应用在该集成电路板上。无铅焊点成为了电子元件可靠性研究方面一个突破点。