基于GIS技术的雷达地形遮挡盲区高度快速计算方法

李冠运， 刘松涛

(1.中国人民解放军92001部队， 山东 青岛 266000；2.海军大连舰艇学院， 辽宁 大连 116018)

0 引 言

雷达探测时会受到地形遮挡、大气折射、地面杂波等多种因素影响，其中，地形遮挡因素对雷达探测造成的影响最为稳定且难以克服[1]。对于雷达使用者来说，弄清自身因地形遮挡造成的探测盲区分布是十分必要的。求解雷达地形遮蔽盲区的传统方法是基于通视关系的几何求解方法，该方法简易快捷、能够实现定量计算，但必须准确定位遮挡点，并获取遮挡点海拔高度及与雷达的地表投影距离，这对基层雷达站来讲几乎不具备可行性。近年来，基于地理信息系统(Geographic Information System，GIS)技术的解算方法不断出现，常用的有基于图形处理器(Graphics Processing Unit，GPU)的雷达可视域分析[2]、模糊评价法[3]、转盘爬虫法[4]、数字高程模型(Digital Elevation Model，DEM)一般求解法[5]等，优点是便于快速计算广域盲区分布并实现可视化，缺点是方法复杂，对编程基础要求高，并且难以修正大气折射带来的误差。

针对上述不足，本文认为地理关系解算能力是GIS技术的基本功能，仅需轻度使用便可为传统求解方法提供关键计算量，两者结合能够高效精准地解算雷达地理遮挡盲区。基于此，提出一种基于GIS技术的雷达地形遮挡盲区高度快速计算方法，主要思路是使用GIS软件的基础功能获得关键计算数值，继而运用解三角形的方法快速求解出雷达盲区的具体分布。该方法能帮助基层雷达站快速求解盲区分布，并为GIS软件开发者提供了一种优化算法的思路，具备较好的实用性。

1 雷达地形遮挡盲区高度计算方法

从实际问题入手，设计给出雷达地形遮挡盲区高度计算方法。假设有雷达A，其某一方向存在高山B遮挡，导致其产生低空遮挡盲区，求距雷达L1+L2外的雷达探测盲区高度。

1.1 不考虑大气折射情况

若雷达波束以标准直线传播，则有图1所示的几何关系。图中，雷达A海拔高度为h1，其雷达探测波束被B山遮挡，导致其在L1+L2外的F点上空产生高度为h3的遮挡盲区。

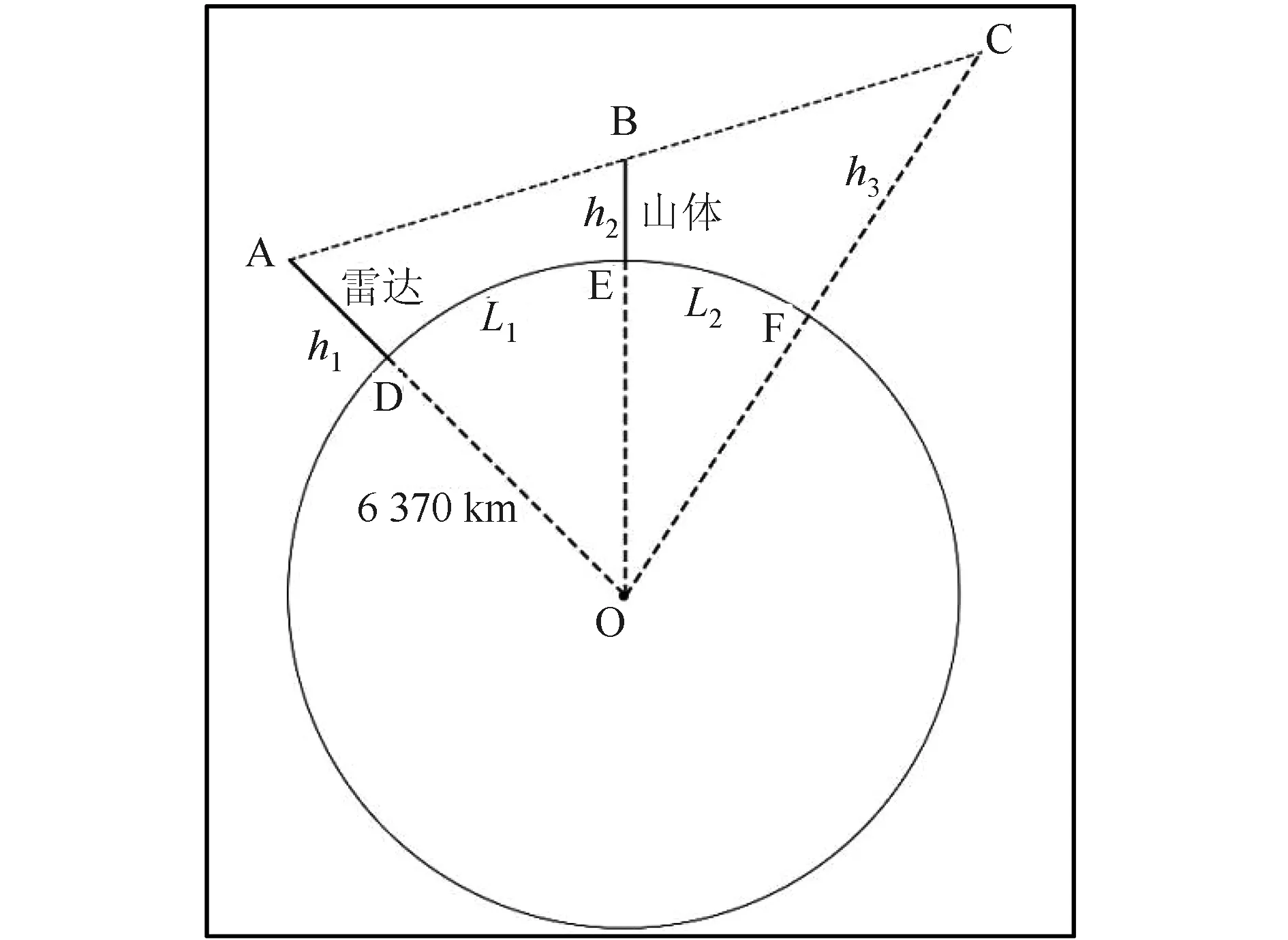
图1 不考虑大气折射情况下的几何关系

不难看出，求解h3的关键在于要知道遮挡体与雷达的遮挡关系，如果准确获取了雷达与遮挡体的地表投影距离L1及遮挡体高度h2，则问题就变成了求解三角形。

由于L1已知，则∠AOB可求，由AO、BO的值，可求∠ABO，计算公式为

∠AOB=(L1×2π)/(6 370×2×π)

(1)

由余弦定理可得：

(2)

∠ABO=arccos[(AB2+BO2-AO2)/(2×AB×BO)]

(3)

则有

∠CBO=π-∠ABO

(4)

由于L2已知，∠BOC可求，∠CBO、BO均已知，则△BOC可求，具体计算如下：

∠BOC=(L2×2π)/(6 370×2π)

(5)

∠BCO=π-∠BOC-∠CBO

(6)

由正弦定理可得：

OC=BO·sin∠CBO/sin∠BCO

(7)

h3=OC-6 370

(8)

1.2 考虑大气折射情况

在实际大气环境下，大气折射指数垂直变化梯度dn/dh随高度变化，导致电磁波传播射线变得弯曲，使雷达传播路径不再是一条直线而是曲线，由此也造成了地形遮挡运算发生了变化。根据文献[6]，当求解高度位于近地面对流层且对精度要求不高时，通常可以运用等效地球半径法修正折射导致的误差。等效地球变换之后的地球半径变为8 490 km，几何关系变为图2。

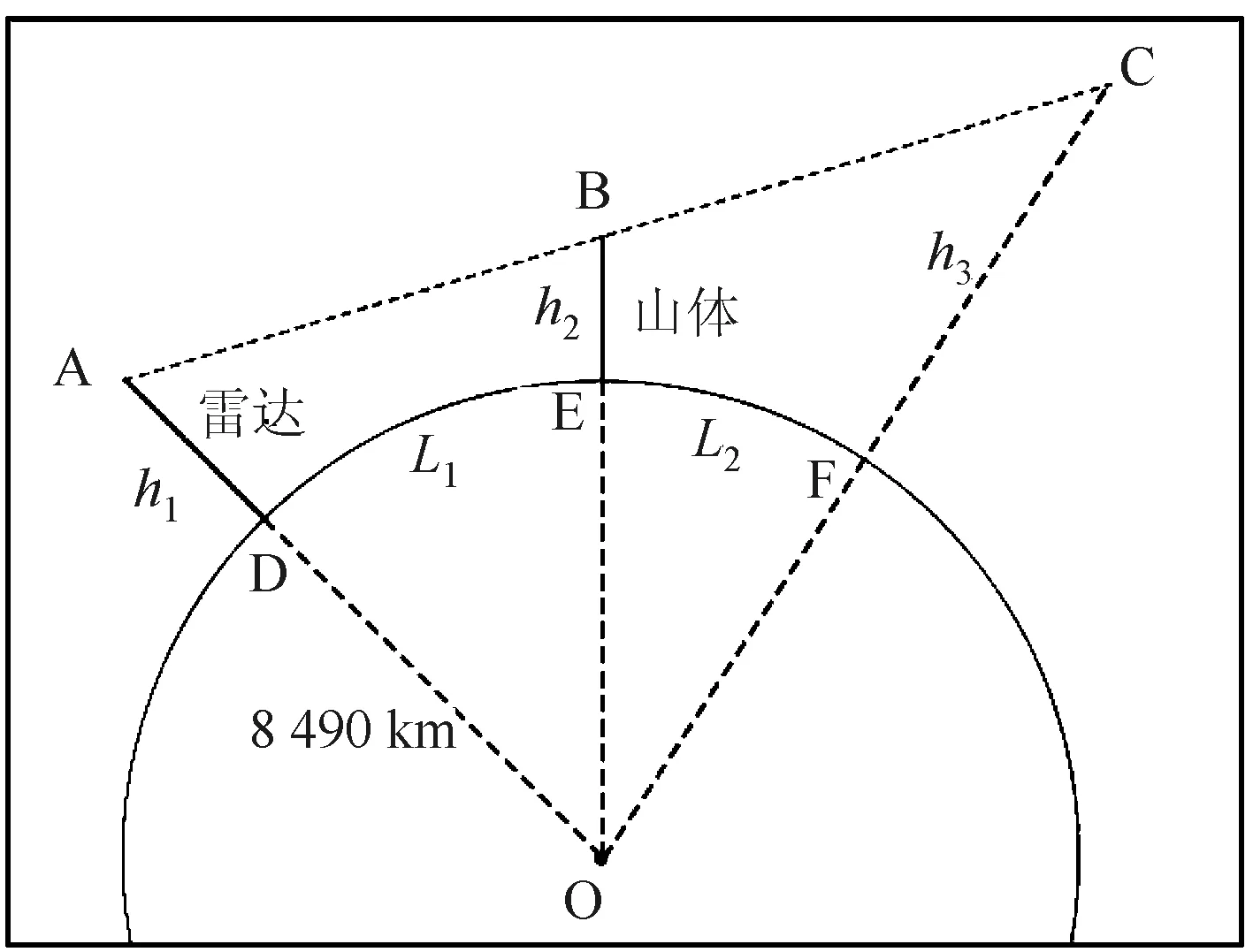
图2 考虑大气折射情况下的几何关系

根据文献[7]，等效地球变换后遮挡物与雷达之间的地心角不变，则L1,等效地球=4/3×L1，标准地球，L1+L2不变。因此，依然可以通过先解△AOB再解△BOC的方法来求解h3，这样就快速解出了雷达在该方向的地理遮挡盲区高度，此处不再赘述。

1.3 通过GIS求解L1、h2

通过以上分析可得，只要知道了遮挡物与雷达之间的地表距离L1以及遮挡物高度h2，便可快速求解不同距离下的雷达遮蔽盲区高度。然而，实际中我们往往很难获得该数据，尤其是计算范围较大时，想要全面定位并测量周边遮挡山体，将是一项非常艰难的任务，极易产生测量误差，GIS技术能解决这类问题。

GIS的点、线等模型，可以定位遮挡物并读取其高度h2；测距功能可以准确测量遮挡点与雷达的地表投影距离L1。求得L1为13.08 km，h2为1 027 m,效果见图3和图4。

图3 GIS对遮挡点的定位情况图

图4 GIS对投影距离的测量示意图

2 特殊情况

由于GIS是基于标准地球的空间数据运算，因此其确定的遮挡点是基于直射情况，同时我们对大气折射的修正是建立在等效地球变换后，仍然是B山对A雷达造成遮挡的情况，这是普遍情况。但也存在一种特殊情况会导致大气折射修正出现错误，如图5所示。

图5 不同条件下的遮挡关系示意图

假设在A雷达与B山连线的后方L3处存在高度为h4的D山，则存在一种可能，即：由于雷达波束由直线变为曲线，使得“绕过”B山的雷达波束又被D山遮挡，这种情况下，由于D山的遮挡造成的雷达盲区的高度理论上比B山遮挡造成的盲区要高，这种情况下，产生决定性遮挡的山体就由B山转变为D山。体现在等效地球中就是，遮挡A雷达的不再是B山，而变成了D山。

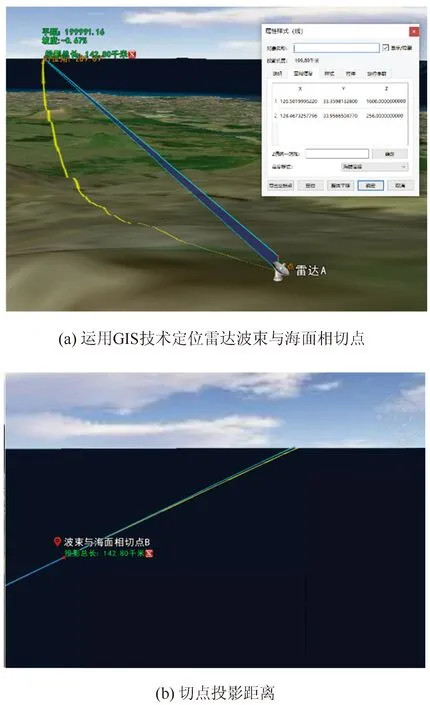
这种情况下，h4必须满足的几何关系条件见图6，即：DG等效地球

图6 解算图

由于h1、h2、L1、L3均已知，可再利用式(1)～(8)分别解算两个DG的值，若D山的高度在该区间内，则应该以D山遮挡的情况来解算雷达盲区。

3 计算实例

假设A雷达海拔高度为1 600 m，海面B造成遮挡，通过GIS测量AB之间的地表投影L1为142.8 km(测量效果见图7)，F点位于距A雷达地表投影距离300 km处。

图7 GIS模拟雷达与海面相切的实现及数据测算示意图

利用视距公式对该方法求解雷达地形遮挡盲区的高度进行检验验证。视距公式的推导本质上也是对遮挡关系的几何运算，是图1和图2中AC与地球海平面相切的情况，该情况下遮挡物的海拔高度为0 m。通过GIS软件寻找到AC与海面的切点，再测量出该切点与雷达的地表投影距离L1，代入式(1)～(8)，若计算结果与视距公式相符，则证明运用GIS技术寻找的遮挡点及测量值准确，且计算方法也可靠。

3.1 标准地球的盲区高度

将数据代入式(1)～(8)，求得标准地球下的F点盲区高度为1 941 m。

根据余弦定理：

300.055 844 6 km

根据标准地球视距公式：

上述两种方法求出的AC值基本相等，证明F点盲区高度求解方法较为可靠。

3.2 修正大气折射后的盲区高度

等效地球法修正大气折射后，AO=8 490+1.6=8 491.6 km，BO=8 490 km，L1,等效地球=4/3×L1,标准地球=190.4 km，数据代入后求得等效地球下的盲区高度为1 015 m。

根据余弦定理：

300.031 171 8 km

根据等效地球视距公式：

上述两个AC值也基本相等，进一步证明F点盲区高度求解方法较为可靠。

4 结 语

针对当前单独运用通视关系的几何求解方法以及GIS技术求解雷达地形遮挡盲区存在的难点，本文提出了一种将两种方法相结合的雷达地形遮挡盲区高度快速计算方法，其核心在于借用GIS技术弄清遮挡关系，获取关键几何量之后，通过简单的解三角形可以较为客观的快速计算盲区分布。计算过程中，要注意运用等效地球法修正大气折射时需要额外考虑是否会产生新的遮挡关系。