基于Volterra 级数的大跨桥梁涡激力内核参数识别方法

■许 坤 王金露 艾四芽 鲍丹宇 余洁歆 许 莉

（1.北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124；2.福州市城乡建设局，福州 350000；3.福建省交通科技发展集团有限责任公司，福州 350004；4.福建省二建建设集团有限公司，福州 350003；5.福建江夏学院工程学院，福州 350108；6.福州大学土木工程学院，福州 350108）

涡激振动是大跨桥梁较易发生的一种大振幅振动现象，对行人行车安全、构件疲劳寿命等产生较大危害。 为掌握结构涡振性能，现有研究往往借助涡激力数学模型，通过风洞试验获取模型气动力参数，结合结构有限元开展三维全桥涡振性能分析， 以考虑结构振型、涡激力展向相干性等三维效应影响[1]。

现有结构涡振模型可大致分为2 类：单自由度模型[2-4]和两自由度模型[5-9]；其中桥梁断面多采用单自由度形式模型。 这类模型通过拟合风洞试验测得的结构位移获取气动力参数。 由于模型无法准确反映涡振过程流体结构间的耦合关系，导致拟合参数在不同质量—阻尼系数工况下存在显著差别。 设计风速内大跨桥梁涡振可发生模态有多阶，不同模态间的模态质量及阻尼比并不相同，基于上述涡振经验模型的计算结果难以保证其可靠性。

近年来，航空航天领域针对全尺寸流固耦合模拟困难开展了降阶模拟技术研究。 其中具有多重卷积积分格式的Volterra 级数理论上可通过无限阶次展开近似任意非线性系统，较适用于模拟气动力的非线性特性及记忆效应。 Volterra 级数早期用于电气工程[10]，Wu 等[11]将其引入到钝体断面非线性气动力模拟，Xu 等[12]则对其用于大跨桥梁涡激气动力模拟开展了初步研究。

为模拟流固耦合行为，需首先获得描述流体—结构耦合关系的气动力内核项。 相较机翼断面，钝体断面流固耦合的非线性效应更为显著，涡振发生风速较低，气动力记忆效应也更为明显。 涡激力中高次内核项的识别问题尤为突出。 针对这一问题，本文采用理论分析和数值模拟手段， 对Volterra 模型非线性最高阶次、气动力记忆持续时长等影响因素进行研究，提出便于实际操作的桥梁断面涡激力内核参数识别方法，并对其准确性进行验证。

1 基于Volterra 理论的涡激力模型

以竖向涡振为例，无量纲结构运动方程可表示为：

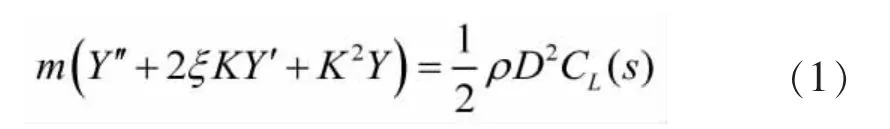
式中， CL（s）为无量纲升力系数；Y 为无量纲位移；K=Dωn/U 为折算频率；s=Ut/D 为无量纲时间；D为结构特征尺寸；ωn为结构振动频率；U 为来流风速；ξ 为结构机械阻尼比；m 为结构质量。

涡振过程中作用于结构的附加气弹效应主要为非线性气动阻尼效应，可将其表示为卷积格式的Volterra 级数形式：

式中，C(1)L表示气动力中的线性项；C(p)L（s）表示气动力中的p 次非线性项；τ1,2,...为气动力记忆效应持续时间；h 为Volterra 级数内核项，其本质为结构运动与气动力间的传递函数。

风洞试验或CFD 模拟得到的结构位移与气动力时程为时间离散格式，有必要将式（3）表示为时间离散格式：

2 Volterra 模型内核识别方法

Volterra 内核识别主要有2 种途径[13]：（1）当被模拟对象具有解析表达式时，可利用解析方法推导Volterra 级数内核解析表达式；（2）当被模拟对象没有解析表达式时，需利用试验或数值模拟得到的系统输入—输出关系，采用系统辨识手段获取Volterra 级数内核参数。

对于钝体断面气动力而言， 无法通过理论推导获得气动力解析表达； 涡激力内核参数只能通过试验或CFD 计算获取所需数据，通过系统辨识手段得到。根据式（6），气动力与结构运动关系可以表示为：

当系统输入—输出总长度大于内核向量总长度时（n+1＞Q1+…+QN），可借鉴最小二乘思想，拟合得到内核向量：

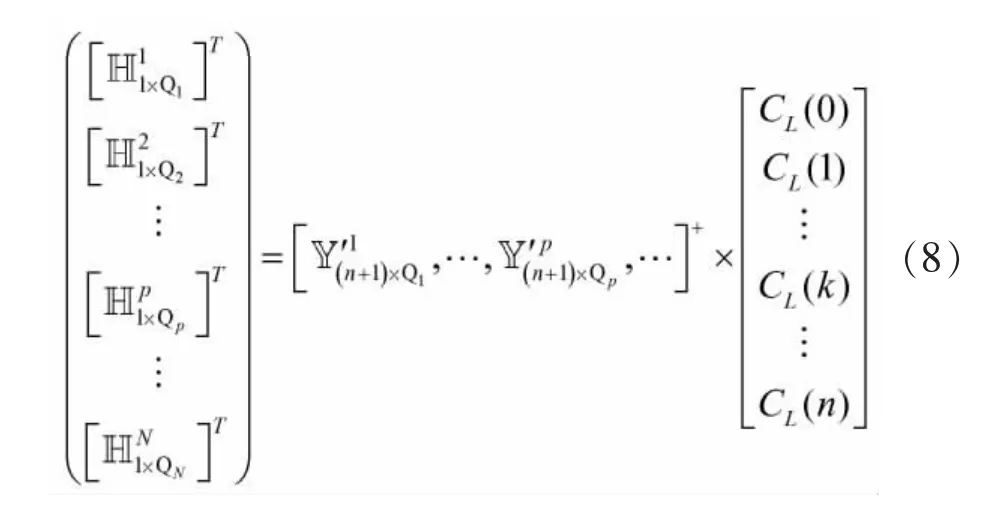
其中，符号“+”表示Moore-Penrose 伪逆。

3 桥梁断面涡激力内核参数识别

为验证桥梁断面涡激力内核识别效果，选取典型π 形断面， 利用CFD 模拟平台获取内核识别所需数据。 计算网格区域为：-15B≤Lx≤35B 和-25B≤Ly≤25B，其中B 为断面宽度，Lx和Ly分别为网格区域在来流及垂直于来流方向的大小。 计算区域采用三角形非结构化网格进行离散，底层网格尺寸为0.001B，总体网格数量约为1.4×105。 计算区域及网格尺寸选取基于前期网格优化验证。 计算过程中雷诺数为1×104（以断面高度为参考尺寸），采用大涡模型进行湍流模拟。 计算区域及网格形状如图1所示。

图1 断面附近局部网格

系统输入—输出数据采用不同折算风速和振幅单频强迫振动组合， 共包括12 个折算风速（1.66≤U/ωnD≤2.15）和10 个无量纲振幅（0.01≤A/D≤0.10）。 各工况采样时长取50 个振动周期。

内核参数识别需首先确定模型最高阶次N 及气动力记忆持续时长Mp。为研究非线性最高阶次和记忆持续时长对模拟效果的影响，对不同N 和Mp条件下的模拟效果进行了比较。 其中，模拟效果评价标准采用Balajewicz 和Dowell 提出的拟合误差率[14]：

式中，yCFD表示CFD 计算结果；yROM表示Volterra模型模拟结果。

拟合误差率如图2 所示，其中时间步长为0.2s（s=Ut/D）， 即Mp取50 时，p 阶 记 忆 持 续 时 长 为0.2×Mp=10s。从图2 可以看到，拟合误差率随模型最高阶次及记忆持续时长的增加而变小，表明模型阶次越高、记忆持续时间越长，模拟效果越好。 当Mp大于一定程度时（如100）时，提高最高阶次N 比增加Mp能获得更好的模拟效果， 这是由于气动力具有记忆衰减特性，Mp大于一定程度时即可较好反映气动力的记忆效应。 为提高模拟效果，应在保证记忆持续时长的基础上尽量提高模型最高阶次。

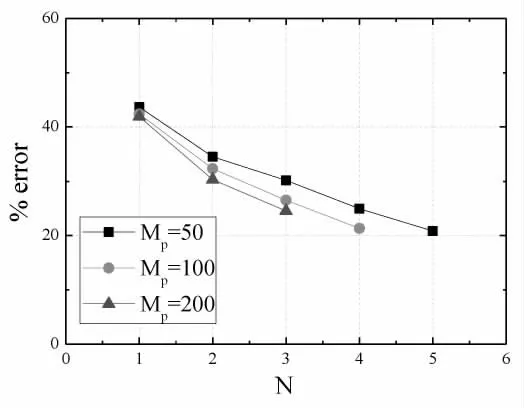
图2 拟合误差率随非线性阶次及记忆时长变化规律

4 内核识别效果验证

为验证内核识别结果， 对Volterra 模型模拟结果与CFD 计算结果进行了比较。 图3 为锁定区前段不同振幅涡激力模拟结果，各振幅下涡激力形状基本一致，为类正弦单组分形式，表明断面漩涡脱落频率完全被结构运动锁定，此时涡激力中与结构振动同频的线性项起主导作用。 图4 为锁定区后段不同振幅计算结果，此时涡激力仍表现出振幅相关特性。 比较图3 和图4 可以发现，锁定区振幅最大点和锁定区后段涡激力中高频与低频成分间的相位差发生了改变，涡激力中高频与低频成分间的相位变化或许是导致锁定区后段涡振随风速增加而逐渐消失的原因。

图3 涡振锁定区前段涡激力时程

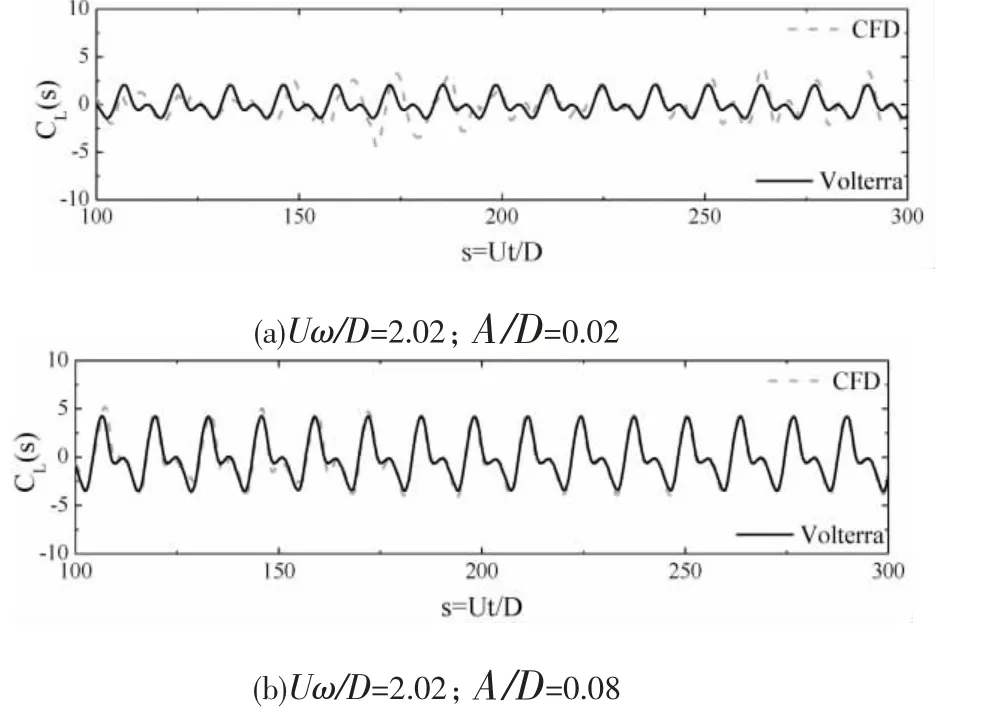
图4 涡振锁定区后段涡激力时程

图5 为锁定区前段涡激力滞回曲线结果。 可以看到，随着振幅增加，滞回曲线逐渐饱满，表现出振幅相关特性。 图6 为锁定区后段结果，与锁定区振幅最大点处不同，该风速下滞回曲线长轴所处象限发生了改变，表明涡激力与结构运动间的相位差发生了变化。 各风速下，缩阶模型均能够较好地模拟原始CFD 结果，验证了内核识别结果的准确性。

图5 涡激力滞回曲线（U/ωD=1.84）

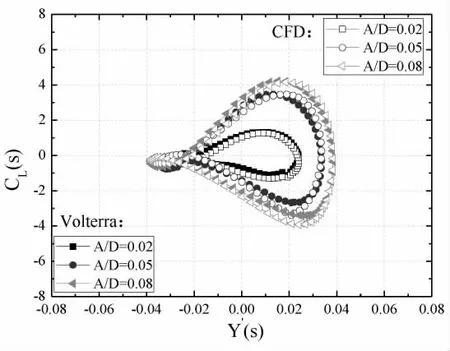
图6 涡激力滞回曲线（U/ωD=2.02）

图7、图8 为不同工况涡激力频谱特性。可以看到，涡激力的非线性特性主要表现为整数倍频效应。 稀疏内核格式的Volterra 模型能够较好模拟这种整数倍频效应，进一步验证了内核识别结果的准确性。

图7 涡激力频谱特性（U/ωD=1.84）

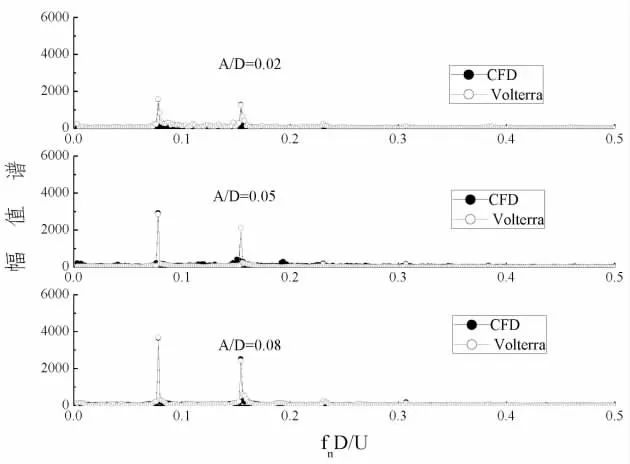
图8 涡激力频谱特性（U/ωD=2.02）

5 结语

本文针对Volterra 级数用于桥梁断面涡激力模拟问题，通过理论分析与数值模拟手段，对涡激力内核识别方法进行了详细验证和比较，得到如下结论：

（1）拟合误差率随模型最高阶次及记忆持续时长的增加而变小。 当记忆持续时长大于一定程度时，提高最高阶次比增加记忆持续时长能获得更好的模拟效果。 为提高模拟效果，应在保证记忆持续时长的基础上尽量提高模型最高阶次。

（2）涡激力的非线性特性主要表现为整数倍频效应，Volterra 级数模型在时域、频域和相空间方面均能较好模拟涡振过程流体—结构间的耦合关系。

（3）采用最小二乘方法的涡激力内核识别过程，无论从风洞试验还是CFD 计算层面均具有较好的可操作性，可用于实际桥梁断面涡激力内核参数识别。