套筒调节阀节流窗口型线参数化设计方法研究

王伟波，郝娇山，周忠云，张丽芳，张建伟

(1.重庆川仪自动化股份有限公司技术中心调节阀研究所，重庆 400707；2.重庆川仪调节阀有限公司，重庆 400707)

0 前言

窗口型套筒调节阀作为工业系统中控制流量的关键元件，被广泛应用于石油、化工、核电领域和液压系统等进行流体控制。由于国内调节阀技术起步较晚，对其等百分比流量特性曲线和线性流量特性曲线相应的节流窗口型线研究较少，且大部分企业沿用的依旧是20世纪90年代进口的国外技术，其选型规格少，流量系数选择范围窄，已不能适应现代多元化工艺过程。对于特殊的节流窗口往往需要大量时间并依靠经验进行设计，且设计精度较低。为弥补套筒调节阀节流套筒设计方法的不足，开展节流套筒窗口的参数化设计研究意义重大。

本文作者针对调节阀小开度调节平缓、大开度调节及时的工况需求，根据流体力学、流量特性、窗口型线几何方程的相关理论，以可调比为50∶1的套筒调节阀为例，对其等百分比流量特性的窗口型线进行了参数化设计的理论推导和研究，并通过仿真和试验进行验证。

1 窗口型线设计的理论研究

节流套筒窗口型线影响着窗口型套筒调节阀的调节性能以及整个阀门管路系统运行的可靠性和稳定性，其流量方程如式(1)所示:

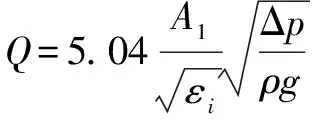
(1)

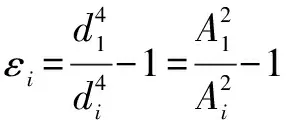
(2)

式中：为调节阀入口面积，单位为cm；Δ为调节阀入口至最小节流处的压差，单位为10Pa(100 kgf/cm)；为流体密度，单位为g/cm；为调节阀开度时的流阻系数；为重力加速度，单位为 cm/s；为流体流量，单位为 cm/s；为调节阀入口直径，单位为cm；为调节阀最小节流处的当量直径，单位为 cm；为调节阀开度时的最小流通面积，单位为 cm。

根据式(1)，调节阀开度时的流量系数被定义为v，如式(3)所示:

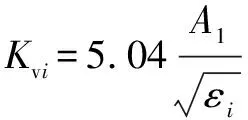
(3)

另外，在调节阀行业，流量系数为阀门的固有特性，是选型的重要参数之一，通常由v表示，根据GB/T 17213.9—2005中的规定，将v转换为v，如式(4)所示：

v=1.156v

(4)

联立式(2)(3)(4)可得，套筒调节阀%开度时的节流套筒流通面积如式(5)所示：

(5)

由于公式(1)的推导中未考虑实际流体流动过程中的能量损失，故在式(5)加入修正系数(具体值可根据设计的精度，通过仿真计算进行确定)对其进行修正，则节流套筒最终流通面积计算公式如式(6)所示：

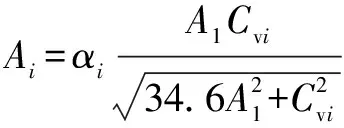
(6)

同理,调节阀(+1)开度时的节流套筒流通面积如式(7)所示:

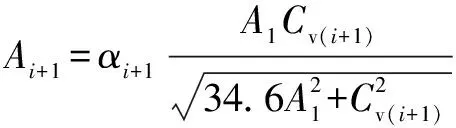
(7)

通过式(6)和式(7)可确定调节阀由开度到(+1)开度时节流套筒流通面积的变化量Δ：

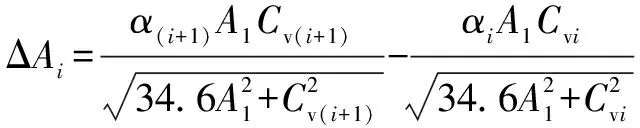
(8)

建立等百分比流量特性的窗口型节流套筒的窗口模型，如图1所示。其中，坐标(+1,+1)处对应的节流面积为+1，坐标(,)处对应的节流面积为。

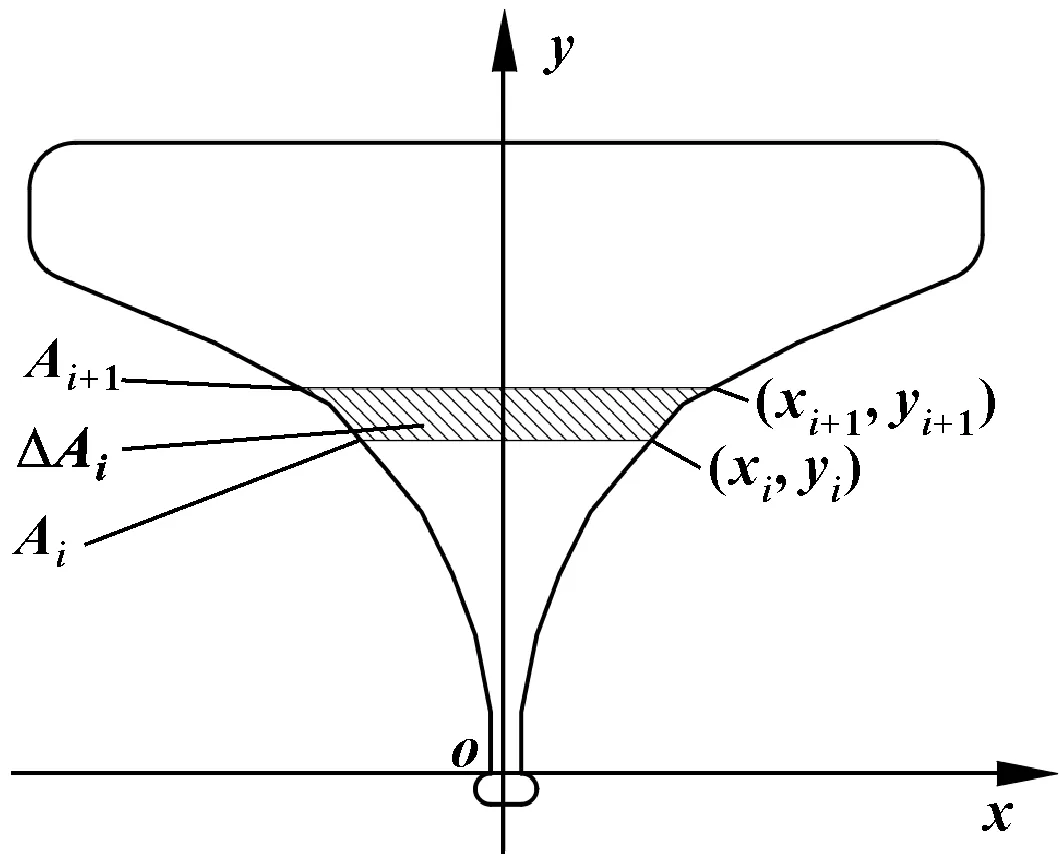
图1 节流窗口模型示意

则有：

Δ=(++1)(+1-)

(9)

当阀门前后压差一定时，调节阀的等百分比流量特性方程如式(10)所示：

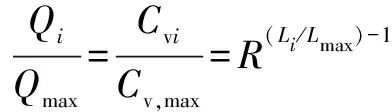
(10)

式中：和分别为调节阀开度和全开时的流量，单位为m/h；和分别为调节阀开度的行程和全开时的行程，单位为mm；为调节阀的可调比。

由此，在阀门进口面积、额定流量系数(即阀门100%开度时的流量系数)、可调比和额定行程给定时，通过仿真确定各开度修正系数(为各开度修正系数的总称)。联立式(8)(9)(10)，可确定套筒调节阀节流窗口的型线坐标，进而可对它开展参数化设计。

2 修正系数确定及节流套筒模型建立

2.1 修正系数确定

文中套筒调节阀窗口型线设计公式中的修正系数通过仿真确定，假定各开度下的设计与理论误差小于±10%时，两阀门控制精度可满足设计要求，则确定方法如图2所示。其中，为、、、…、的总称，与、、、…、依次对应。

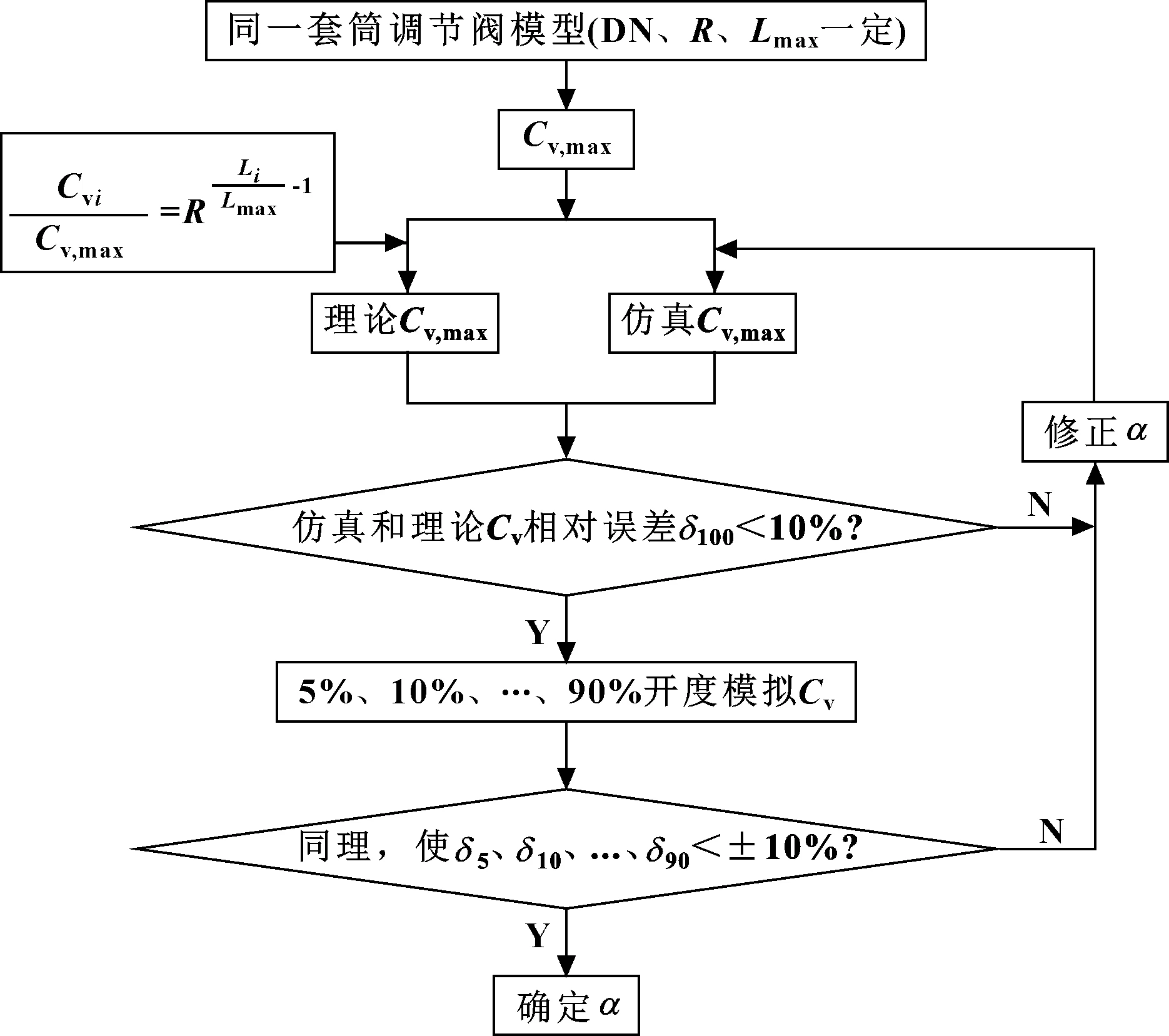
图2 确定修正系数的原理

当修正系数确定后，针对同一个口径的套筒调节阀，流量系数在一定范围内变动时，具有一定的适用性，即在该范围内可实现节流套筒窗口型线的参数化设计。其中，的变动范围需根据阀门各开度调节精度的需求进行确定。

2.2 节流套筒模型建立

以可调比为50∶1的DN80-(44)套筒调节阀和DN200-(275)套筒调节阀为例，进行节流套筒模型的建立。其中，DN80-(44)套筒调节阀主体模型如图3所示。

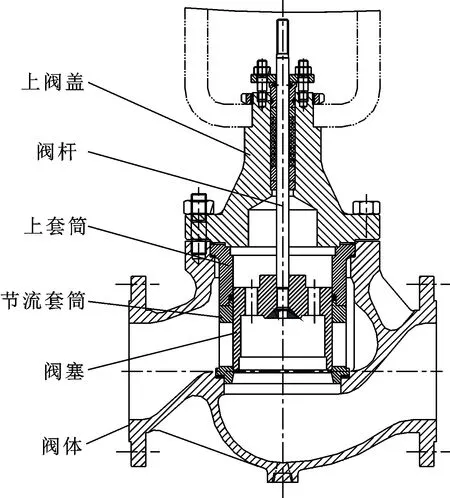
图3 DN80-Cv，max(44)套筒调节阀主体模型

DN80-(44)套筒调节阀额定行程为38 mm，考虑阀塞与阀座间的配合尺寸及对与可调比相关的最小流量系数对应的高度需求，结合图1坐标关系，窗口型线的实际设计行程取35.03 mm，则与阀门开度对应的窗口行程(mm)=35.03-38×(1-%)。同理，DN200-(275)套筒调节阀额定行程为75 mm，取窗口型线的实际设计行程为70.03 mm，则与阀门开度对应的窗口行程(mm)=70.03-75×(1-%)。将两阀门窗口对应的各开度行程和设计行程代入公式(10)，计算得到其各开度下的理论流量系数，如表1所示。

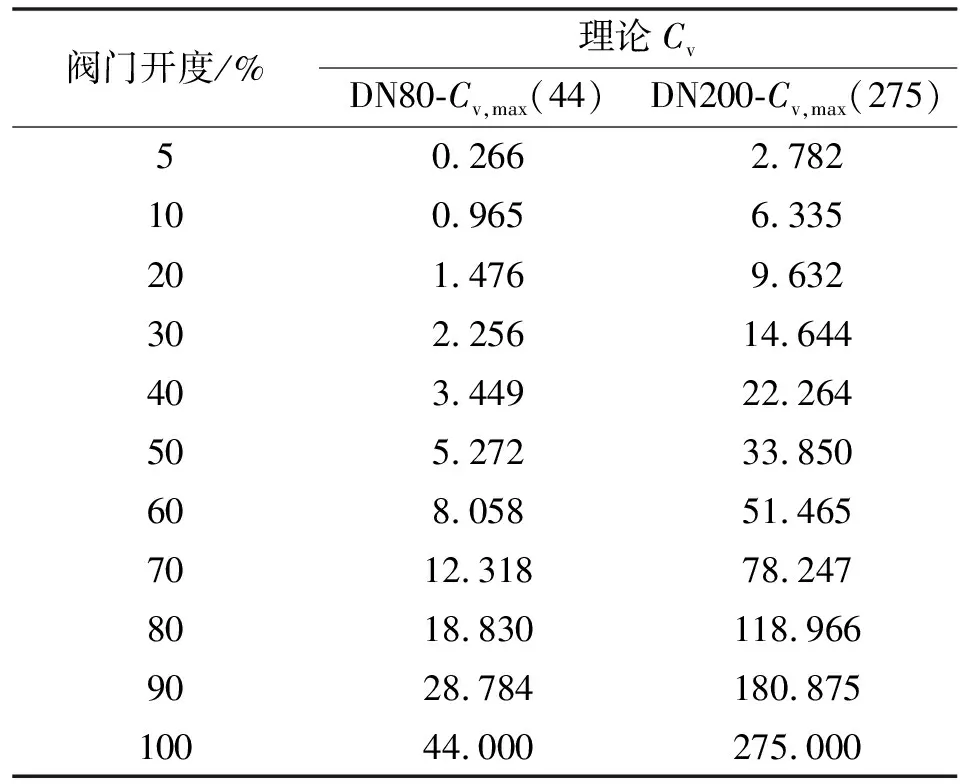
表1 理论流量系数

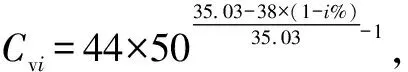
根据修正系数确定方法及参数化设计原理，最终所设计的两阀门窗口型线如图4所示，节流套筒三维半剖模型如图5所示。

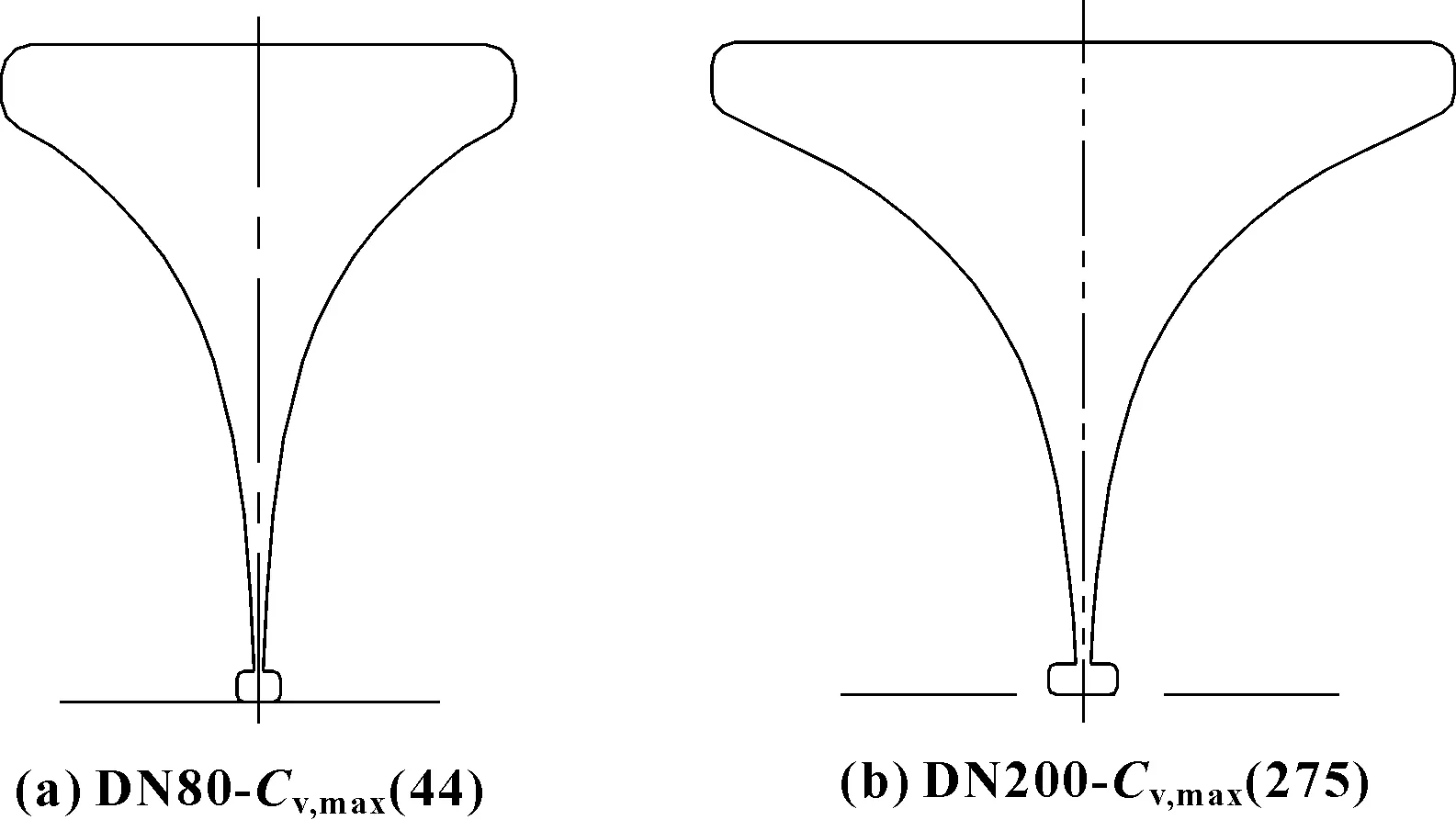
图4 节流窗口型线

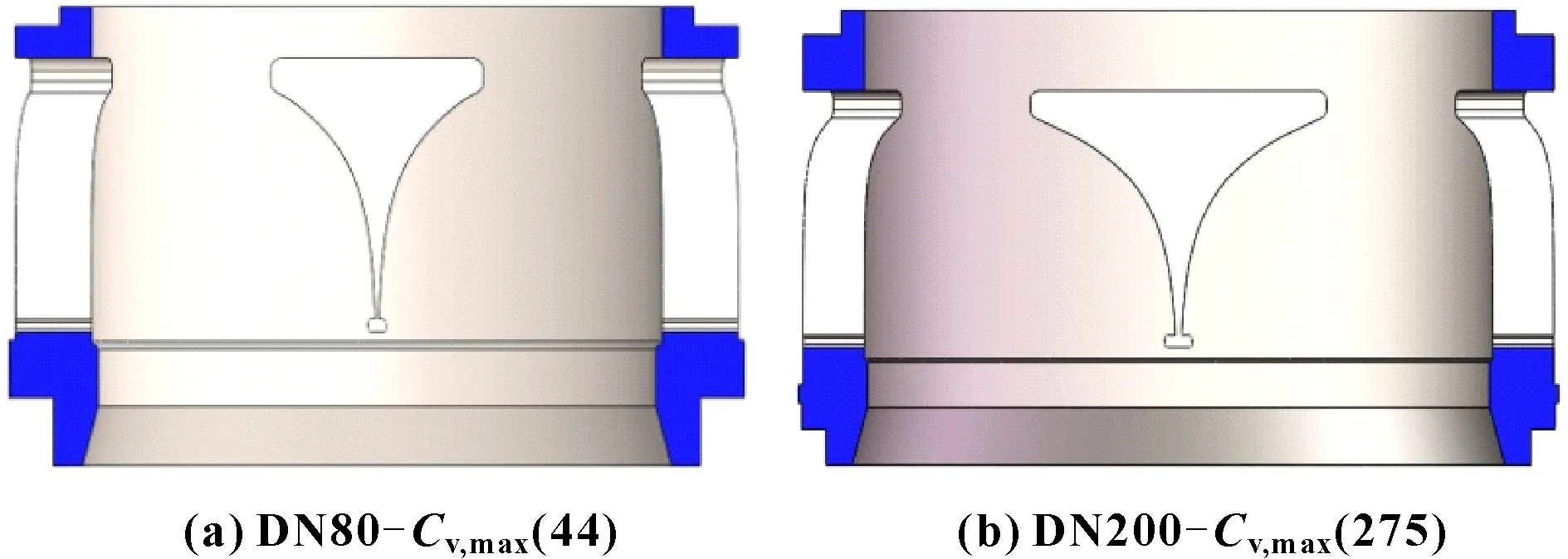
图5 节流套筒三维半剖模型

3 流场仿真分析

分别对DN80-(44)套筒调节阀和DN200-(275)套筒调节阀5%、10%、20%、…、100%开度的三维模型进行仿真分析，验证其节流套筒的窗口设计精度。

3.1 流场仿真理论

因RNG-湍流双方程模型除了修正了湍流黏度，还考虑了流体流动中的旋转情况以及时均应变率，提高了模拟精度。故此套筒调节阀稳态流场计算中，基于连续性方程、动量方程和能量方程，采用该方程构成封闭方程组，其理论如式(11)、(12)所示。

(1)湍动能方程：

(11)

(2)湍流耗散率方程：

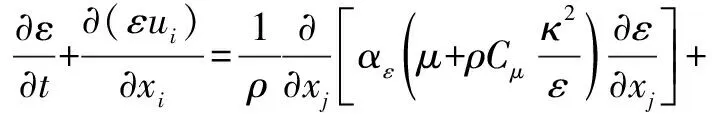
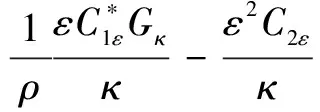
(12)

式中:为平均速度梯度引起的湍动能生成项。

其中：

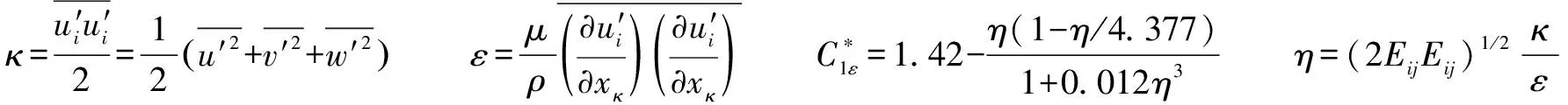
3.2 流道模型建立

阀前管道长度取2倍管道公称通径，阀后管道长度取6倍管道公称通径。将与修正系数对应的套筒调节阀各节流开度三维模型另存为.x-t 格式，导入ANSYS Fluent软件中，反向建模生成内流道模型。另外,考虑阀塞、上套筒和阀盖所组成的中腔对介质的流量系数影响很小，故对它进行适当简化，其中两阀门100%开度内流道半模型如图6所示。

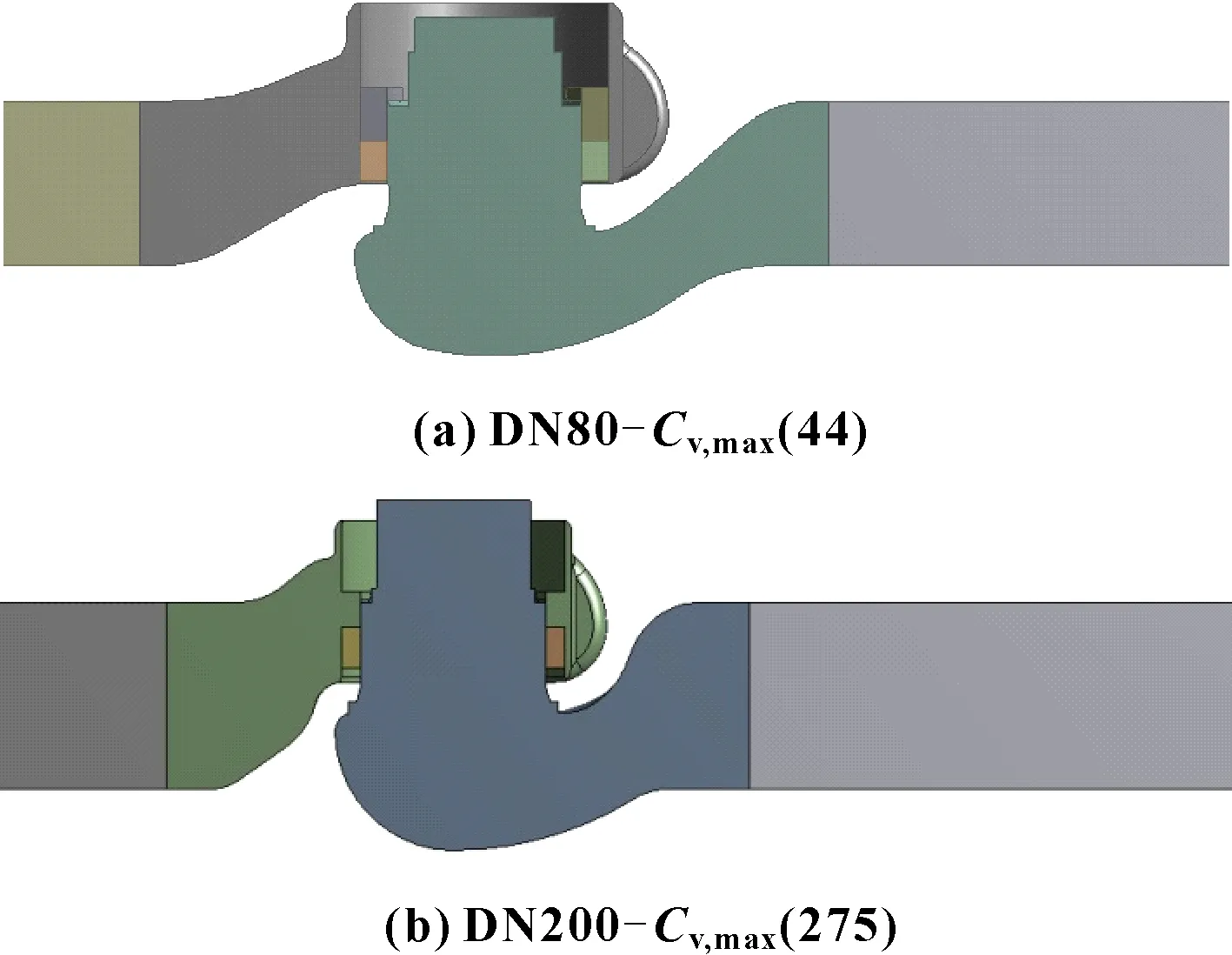
图6 内流道半模型(100%开度)

3.3 网格划分

套筒调节阀内流道模型网格由ANSYS Meshing软件划分生成，采用四面体/混合网格的划分方法，对流道节流窗口处及拐弯处进行局部加密，并以阀门出口流量及出口流体平均流速作为评判依据，对它进行网格无关性检验。以DN80-(44)套筒调节阀全开内流道网格模型为例进行无关性检验说明，具体数据如表2所示。

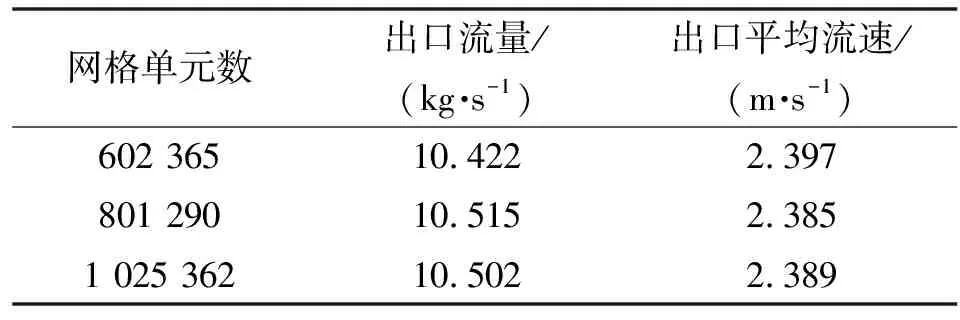
表2 流体域网格无关性检验数据(DN80-Cv，max(44))

由表2可知：网格数从602 365增大到801 290时，流量从10.422 kg/s变为10.515 kg/s，增加0.89%，速度从2.397 m/s变为2.385 m/s，减小0.5%;网格数从801 290增大到1 025 362时，流量从10.515 kg/s变为10.502 kg/s，减小0.12%，速度从2.385 m/s变为2.389 m/s，增大0.17%。相比较而言，当网格数达到801 290以上时，流量及速度的变化可以忽略不计。同时考虑模拟计算精度、时间成本和工作量，以网格数为801 290的流道网格模型作为DN80-(44)套筒调节阀全开时的最终流场仿真模型。

DN80-(44)套筒调节阀和DN200-(275)套筒调节阀100%开度的内流道网格模型如图7所示。

图7 内流道网格模型

3.4 参数设置及流场分析

(1)参数设置

根据GB/T 17213.9—2005中要求，开展套筒调节阀三维定常流动数值模拟。介质为液态常温水；进口采用总压入口200 kPa，出口采用静压出口100 kPa；壁面采用光滑、无滑移壁面边界；收敛条件为连续性方程、动量方程以及湍流方程的最大残差均小于1×10，能量方程的最大残差小于1×10；以阀门入口参数作为初始条件，采用Standard Initialization；环境压力设定为0，且考虑重力加速度对流体流动的影响；Number of Iterations设置为2 000。

(2)流场分析

以DN80-(44)套筒调节阀和DN200-(275)套筒调节阀80%开度横截面的流场为例，进行流场分析说明，分别如图8和图9所示。

由图8(a)可知:阀门入口至节流套筒前端及阀门出口段未形成较明显的漩涡，流体流经节流套筒窗口后，在阀塞的内侧及阀门底部左侧形成较大漩涡，在节流窗口处，流速急剧增大，局部最大流速可达14.05 m/s。由图8(b)可知：流场横截面最大压力为199.9 kPa，位于阀门进口至节流套筒之前的区域，流体流经节流窗口后，压力开始下降，在漩涡区域及阀门出口段的压力约为100.8 kPa，在节流窗口处，局部最低压力可达75.97 kPa。

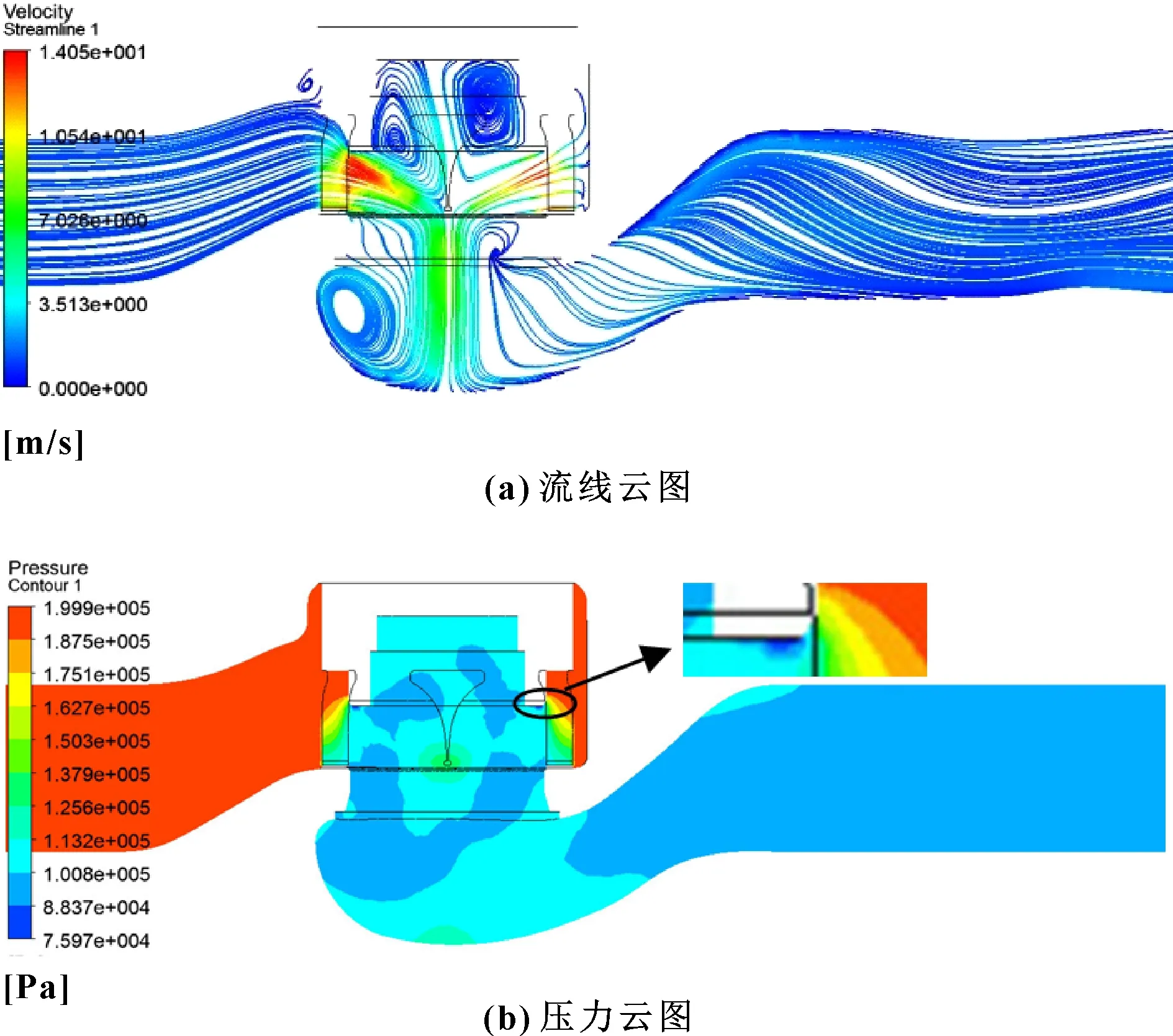
图8 DN80-Cv，max(44)套筒调节阀80%开度横截面流场云图

由图9(a)可知：阀门入口至节流套筒前端及阀门出口段，未形成较明显的漩涡，流体流经节流套筒窗口后，在阀塞的内侧形成较大的漩涡，在节流窗口处，流速急剧增大，局部最大流速可达14.03 m/s。由图9(b)可知：流场横截面最大压力为199.9 kPa，位于阀门进口至节流套筒之前的区域，流体流经节流窗口后，压力开始下降，在漩涡区域及阀门出口段的压力约为105.2 kPa，在节流窗口处，局部最低压力可达64.64 kPa。

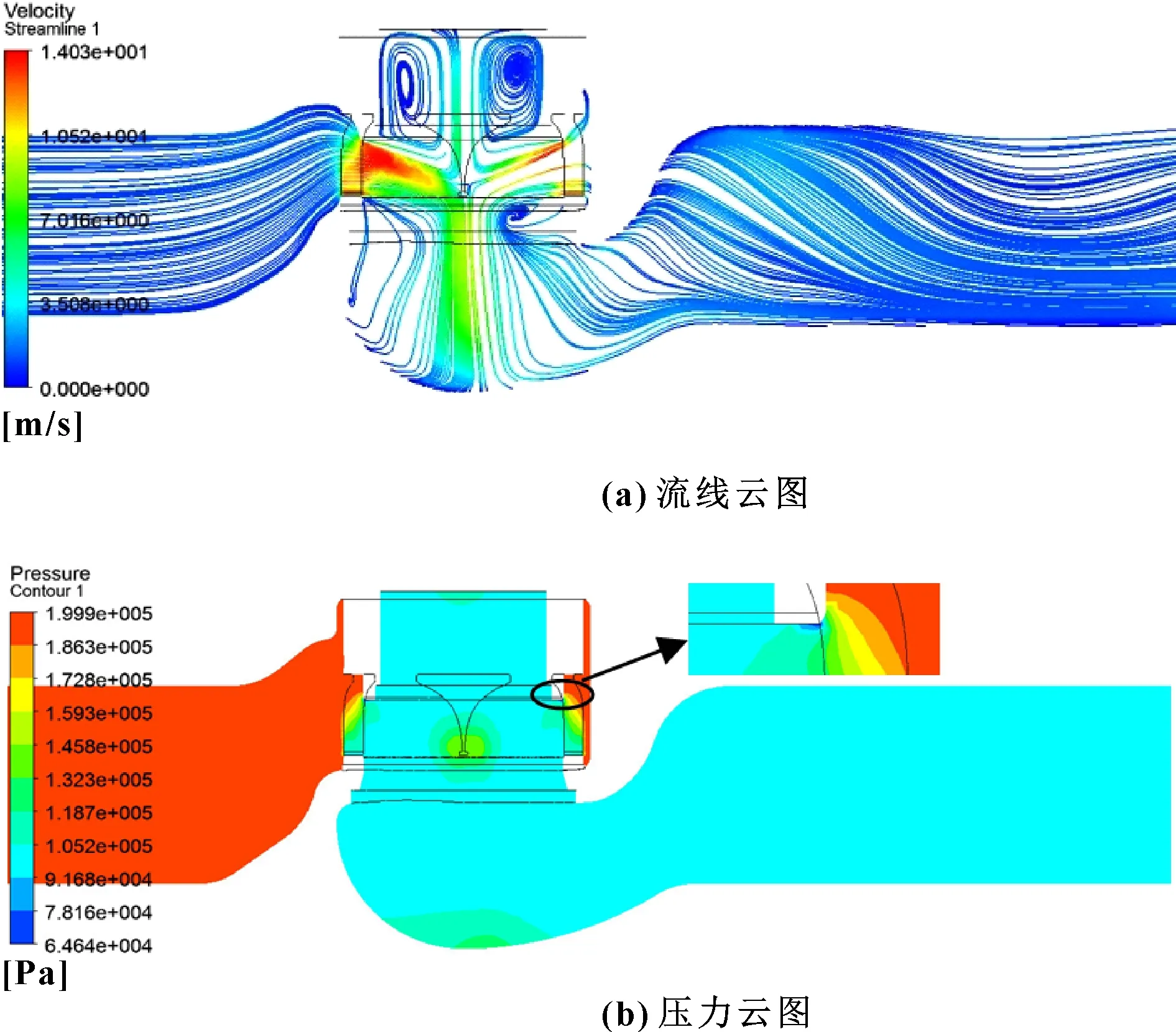
图9 DN200-Cv，max(275)套筒调节阀80%开度横截面流场云图

3.5 仿真流量系数计算

调节阀流量系数计算公式如式(13)所示:

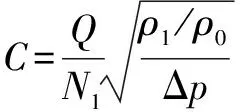
(13)

式中：为被测体积流量，单位为m/h；Δ为阀门上游取压口和下游取压口的压力差，单位为kPa；为流体密度，单位为kg/m；为15.5 ℃时的水密度，单位为kg/m;为数字常数,取0.086 5。

将DN80-(44)套筒调节阀和DN200-(275)套筒调节阀各开度仿真流量及压差代入式(13)，可得到相应的仿真流量系数。进行仿真流量系数与理论流量系数之间的相对误差计算，结果如表3所示。

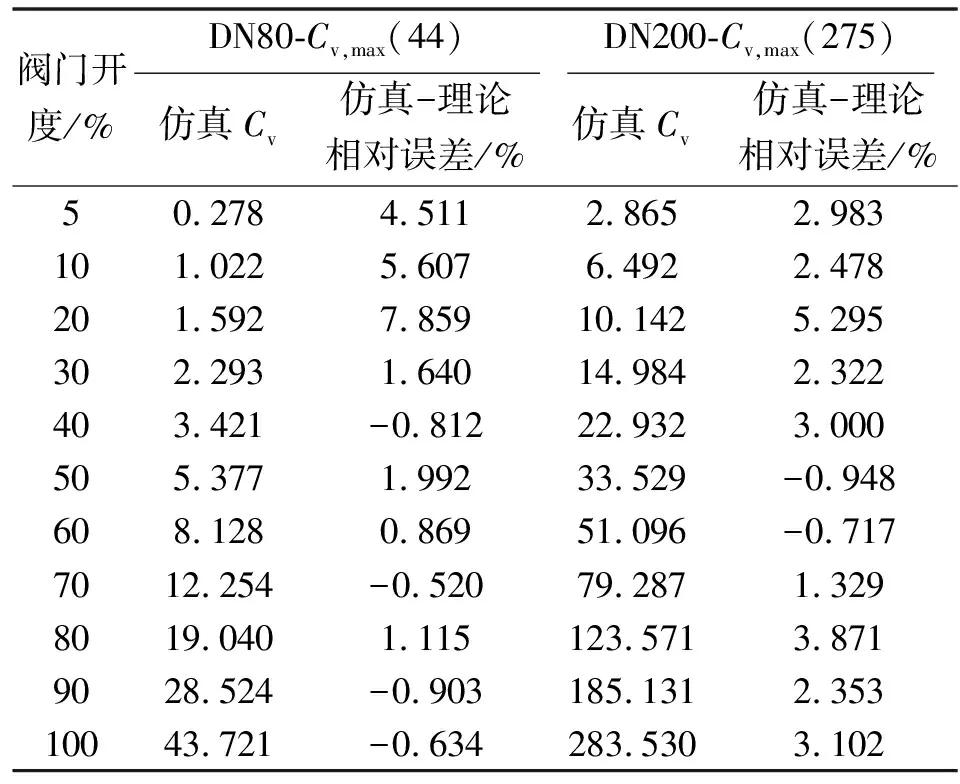
表3 仿真流量系数和理论流量系数相对误差

由表3可知，理论与仿真相对误差均在±10%以内，两调节阀的节流窗口精度满足设计要求，即两调节阀各开度下流量控制精度满足设计要求。

4 流量试验分析

根据所设计的DN80-(44)套筒调节阀和DN200-(275)套筒调节阀的节流套筒窗口型线，采用线切割进行其窗口加工，最终节流套筒实体模型如图10所示。

图10 节流套筒实体模型

4.1 试验说明

依据GB/T 17213.9—2005，分别进行DN80-(44)套筒调节阀和DN200-(275)套筒调节阀的流通能力试验。

流量试验中，信号发生器的作用是提供4～20 mA的电流信号，当定位器接收到不同电流信号时，调节阀便可进行相应的行程调节，从而改变开度。千分表用来监测行程的调节精度，保证行程和开度准确对应。阀门前后压力稳定时，采用压力表读取调节阀前后取压口之间的压力差，另外在控制室读取调节阀流量。最终记录阀门在5%、10%、20%、…、100%开度下的流量和压差，每个开度进行3组试验，每组试验流量和压差一一对应。试验台如图11所示。

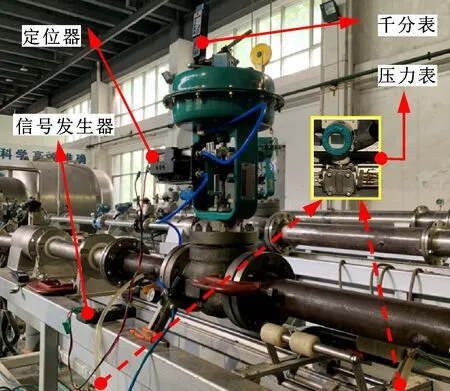
图11 套筒调节阀流通能力试验装置

4.2 试验流量系数计算

根据试验测试数据，通过式(13)进行DN80-(44)套筒调节阀和DN200-(275)套筒调节阀各开度时的计算。每个开度最终值取3组试验值的算术平均值，结果如表4所示。

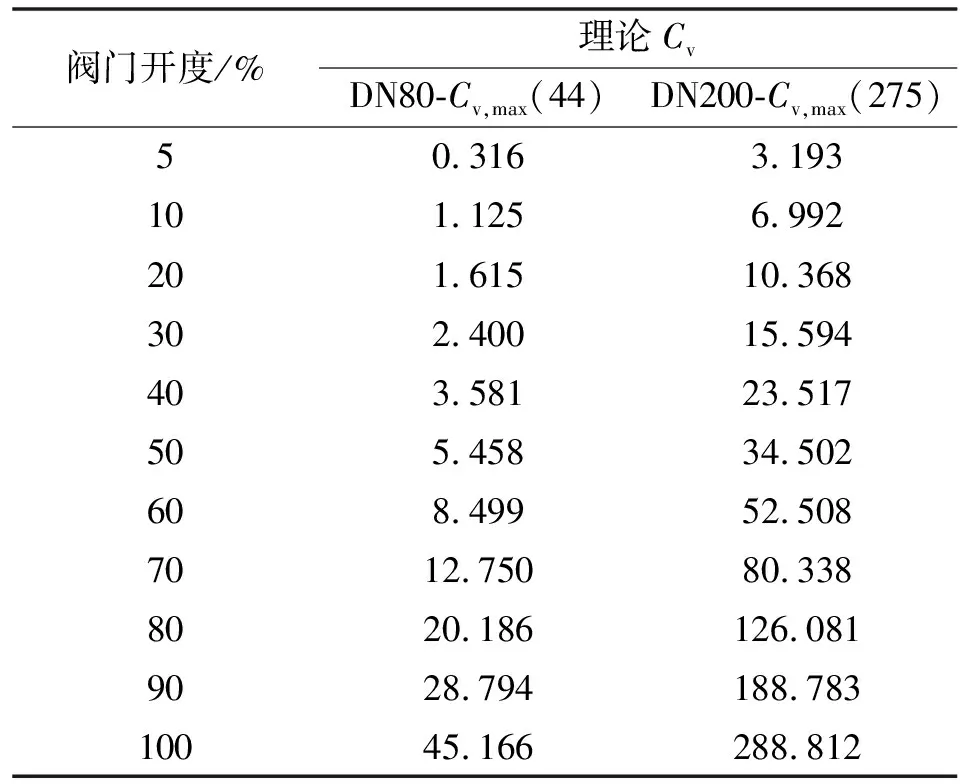
表4 试验流量系数

4.3 流量特性曲线分析

通过DN80-(44)套筒调节阀和DN200-(275)套筒调节阀的理论流量系数、仿真流量系数和试验理流量系数相关数据，绘制相应的流量特性曲线，如图12所示。

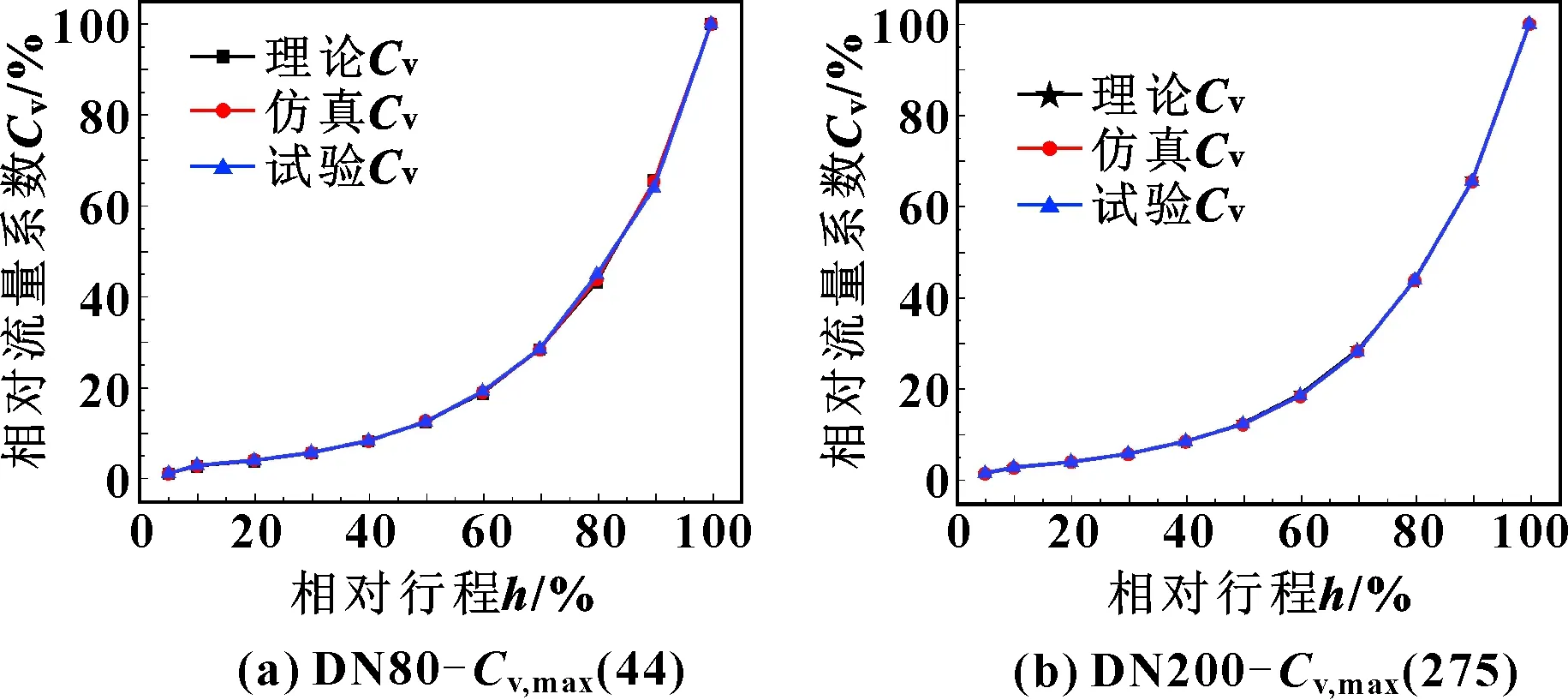
图12 套筒调节阀流量特性曲线

由图12可知：对可调比为50∶1的两调节阀，理论流量特性曲线、仿真流量特性曲线和试验流量特性曲线三者高度吻合。

4.4 误差分析

DN80-(44)套筒调节阀和DN200-(275)套筒调节阀的试验流量系数和仿真流量系数的相对误差如表5所示。

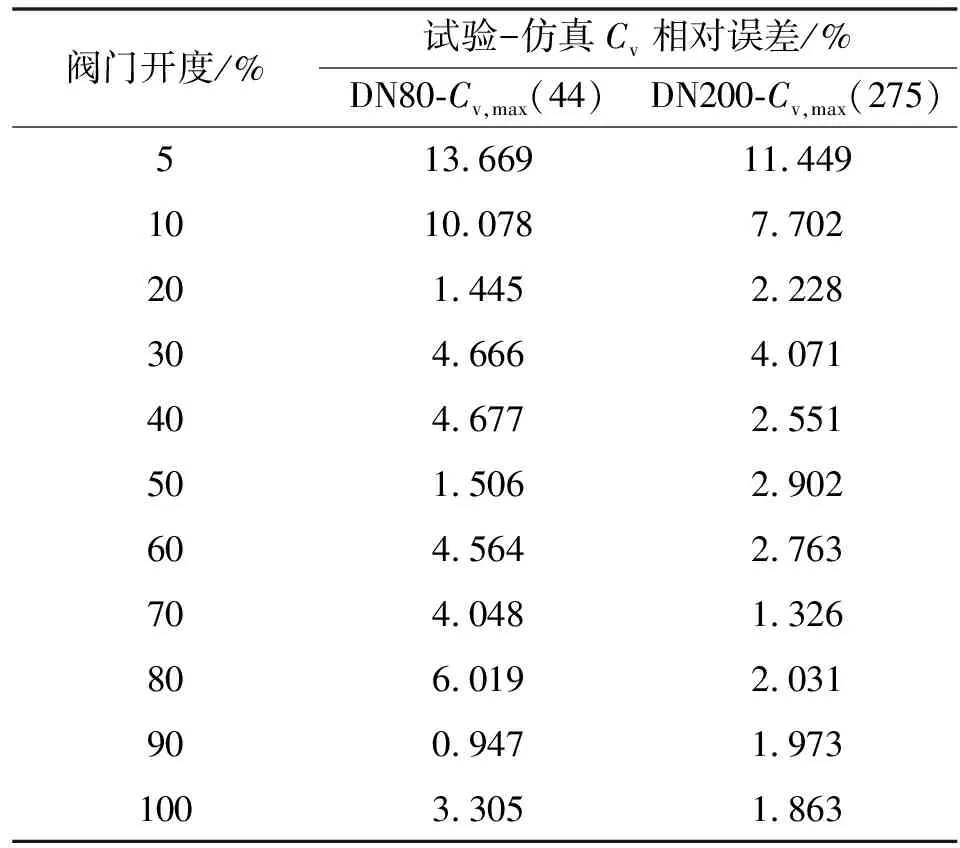
表5 试验流量系数和仿真流量系数相对误差

由表5可知:对于DN80-(44)套筒调节阀，5%和10%开度时，试验-仿真流量系数相对误差均大于10%，20%～100%各开度，试验-仿真流量系数相对误差均小于10%；对于DN200-(275)调节阀，5%开度时，试验-仿真流量系数相对误差大于10%，10%～100%各开度，试验-仿真流量系数相对误差均小于10%。

另外，两阀门各开度下的试验-仿真流量系数相对误差均为正误差，即试验流量系数均大于仿真流量系数。主要原因是试验模型和仿真模型本身存在差异，为了防止阀芯与阀塞装配时存在干涉问题，试验模型设计有配合公差，因此两者间不可避免地会存在环向间隙，且其大小由所设计的公差和加工精度决定。而仿真模型为理想模型，节流套筒和阀塞间没有环向间隙。因此，试验时两阀门各开度下的流量实际由间隙处的流量和流经节流套筒的流量两部分组成，且开度越小，环向间隙对流量的补偿越大，故两台阀门试验流量系数均大于仿真流量系数，这也是导致两阀门5%和10%开度相对误差较大的原因。

5 结论

本文作者通过理论分析，对套筒调节阀等百分比流量特性的窗口型线参数化设计进行了研究，并以可调比为50∶1的DN80-(44)套筒调节阀和DN200-(275)套筒调节阀为例，进行了窗口型线设计，并采用仿真和试验进行了分析验证。得到以下结论：

(1)介质流经两阀门时，在其横截面上，节流窗口处均形成最大流速和最低压力，且在阀腔内部均形成大量漩涡；

(2)两调节阀的理论流量特性曲线、仿真流量特性曲线和试验流量特性曲线三者高度吻合，验证了套筒调节阀节流窗口型线参数化设计的可行性及合理性；

(3)两调节阀5%和10%开度时，试验流量系数和仿真流量系数相对误差均较大，20%～100%各开度相对误差均较小，即两阀门在20%～100%之间进行调节时，流量控制精度较高；

(4)由于试验模型的节流套筒与阀塞之间环向间隙的存在，两台调节阀试验流量系数均大于仿真流量系数，且阀门开度越小，环向间隙对流量的补偿越大；

(5)文中基于设计窗口进行了调节阀理论流量系数的计算与其参数化的设计研究，与调节阀行业中基于阀门额定行程计算的流量系数略有差异。为进一步支撑调节阀的高精度选型，下一步拟开展基于额定行程的套筒调节阀节流窗口参数化设计研究。