改进粒子群优化的双向DC/DC变换器模糊PI控制
龚仁喜,杨元甲,王保平
(广西大学 电气工程学院,广西 南宁 530004)
0 引言
近年来,随着双向直流-直流(direct current-direct current,DC/DC)变换器在工业生产中的应用越来越广泛,对双向DC/DC变换器控制方法的研究也越来越多,并且取得了一些成果。文献[1]运用一种模糊比例-积分-微分 (proportion-integral-differential, PID) 控制双向半桥变换器,提高了控制器的稳定性及自适应能力,但是变换器的响应速度较慢。文献[2]运用模糊比例-积分 (proportion-integral, PI)控制交错并联双向DC/DC变换器,提高了输出电压的响应速度,减小了超调量,并且很好地实现了均流。文献[3]运用模糊PID控制车载交错并联双向DC/DC变换器,有效消除了控制器内部参数变化和外部干扰的影响,增强了控制器的稳定性。文献[4]采用电压电流双闭环控制交错并联双向DC/DC变换器,同时对变换器使用软开关技术,增强了变换器的动态特性和稳态特性。文献[5]将模糊控制运用于车载双向DC/DC变换器,使变换器具有快速响应特性,能够根据车辆的运行情况迅速响应负载变化。文献[6]提出了一种Buck变换器的模糊PID控制方法,该方法不使用传统的数值式模糊变量来描述系统,而是采用语言式,使得控制器适应性能良好。并且,当参数或者负载变化时,该方法也能使变换器保持良好的动态和稳态性能。
但上述控制方法均存在变换器响应速度慢、超调量大,当负载或参考电压变化时,输出电压恢复速度慢、电压波动大等问题。针对以上问题,本文提出一种改进粒子群算法(improved particle swarm optimization,IPSO)优化的交错并联双向DC/DC变换器模糊PI控制方法。该方法运用IPSO,以时间误差绝对值积分(integral of absolute value of time error, ITAE)指标作为算法的目标函数,对双向DC/DC变换器模糊PI控制中的比例因子和量化因子进行寻优。大量的仿真结果表明:该控制方法可有效提升变换器的响应速度,减小超调;当负载跳变或者参考电压跃变时,输出电压能够快速恢复到稳定状态。
1 变换器数学模型及双闭环控制器设计
交错并联双向DC/DC半桥电路结构如图1所示。控制方式采用交错控制,使两个变换器的驱动信号相差半个周期,调制信号和电流波形如图2所示,其中,d为占空比;Ts为开关周期,s;iL1、iL2分别为每一条支路的电感电流,A;iL为两路电感电流之和,A。这样的调制方法,相比单个变换器,减小了开关管的电流应力及电流纹波,并且提高了功率等级。
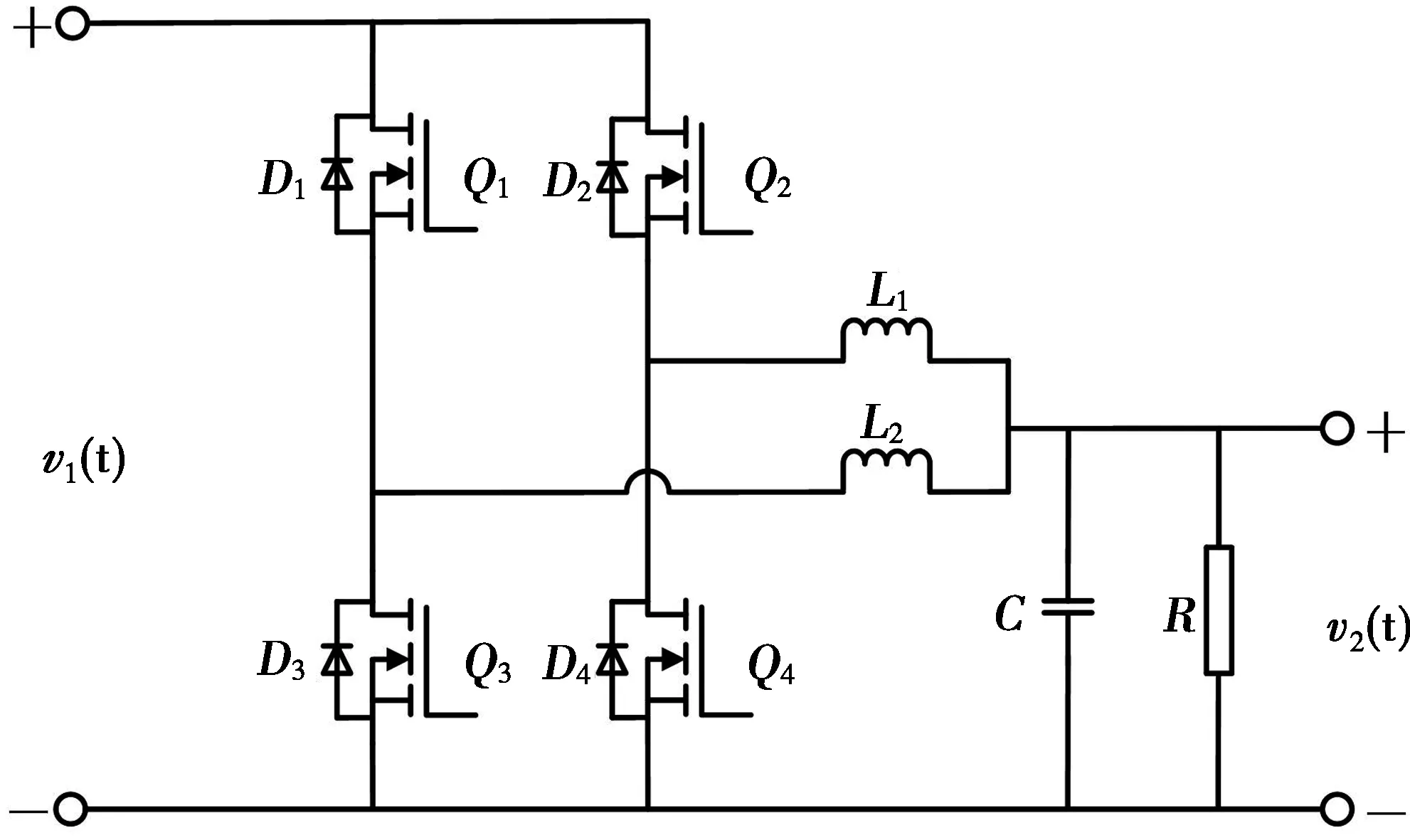
图1 变换器结构图

图2 驱动信号和电流波形图
变换器具有Buck和Boost两种工作模式,分别建立不同模式下的小信号模型。
1.1 Buck模式建模
变换器Buck模式下的等效电路如图1所示,此时,能量流动方向为v1(t)到v2(t)。其小信号方程可表示为:
(1)

图3 Buck模式小信号等效电路模型

由此可得Buck模式小信号等效电路模型,如图3所示。
由上述小信号模型,可得Buck模式下占空比到电感电流、占空比到输出电压以及电感电流到输出电压的传递函数分别为:
(2)
(3)
(4)
1.2 Boost模式建模
变换器Boost模式下等效电路如图4所示,此时,能量流动方向为v2(t)到v1(t)。其小信号方程可以表示为:
(5)

由此可得小信号模型,如图5所示。

图4 变换器Boost模式等效电路图

图5 Boost模式小信号等效电路模型
由上述小信号模型,可得Boost模式下占空比到电感电流、占空比到输出电压以及电感电流到输出电压的传递函数分别为:
(6)
(7)
(8)

图6 双闭环控制框图
1.3 双闭环控制器设计
由上述数学模型,设计变换器的双闭环控制器,如图6所示。
电流环的参考电流由电压环经PI控制后得到,该参考值为两相电感电流参考值之和;每一相电感电流参考值为此参考值的一半。
2 模糊PI控制器设计
2.1 模糊PI控制器结构
将模糊控制施加于双闭环控制的电压外环,通过模糊控制来实时调整电压外环PI控制器中的PI参数。文章设计的模糊PI控制器控制框图如图7所示。图7中,e为电压误差,ec为电压误差变化率,Ke、Kec为量化因子,Kup、Kui为比例因子。
经调整后的PI控制器的比例积分增益可表示为:
(9)

2.2 论域及隶属度函数
模糊推理过程中的输入输出论域采用归一化论域,设置为[-6,6]。模糊语言变量设置为{NB,NM,NS,ZO,PS,PM,PB},对应含义为: 负大、负中、负小、零、正小、正中、 正大。输入输出隶属度函数均采用三角函数和高斯函数,如图8所示。

图8 隶属度函数图
2.3 模糊规则库的设计
不同的电压误差e和电压误差变化率ec值时,电压环PI控制器的控制参数Kp和Ki的调整方向是不同的。过大的e值,会导致系统响应速度慢,并且初始时e值瞬间变大会产生很大的超调量,因此,此时应取较大的Kp;同时,积分作用也会产生很大的超调量,因此,应取较小的Ki值。当e开始由初始较大的值逐渐减小时,为了降低超调量,并保证系统的响应速度,Kp的值应适当减小,Ki的值应适当增大。当e减小到一定值时,应取较大的Kp、Ki值,以免稳态误差过大,影响控制效果[7-12]。
根据上述原则,设计模糊规则表,如表1所示。

表1 模糊规则表
模糊控制中的量化因子和比例因子对控制性能影响极大。量化因子过大,系统会产生超调和振荡,并且会表现得较为迟钝;过小,会导致系统的收敛速度慢。比例因子过大,也会导致系统产生振荡;过小,则会导致系统收敛速度慢[13-15]。并且,量化因子和比例因子一旦根据专家经验确定后则无法改变,系统自适应能力差,控制器性能不高。因此,本文通过IPSO对量化因子和比例因子进行寻优,以此来提高控制性能。
3 基于改进粒子群算法的模糊PI控制参数优化
3.1 改进粒子群算法
在粒子群算法中,惯性权重ω对算法影响极大,传统的线性调整方式存在如下缺点:
(Ⅰ)若群体在早期发现了某些较好的位置,则由于此时所有粒子都具有较大的惯性权值ω,将导致种群对此位置的开发力度不足,从而可能错失对此潜在区域的开发机会[16]。
(Ⅱ)在进化的后期,由于所有粒子都具有较小的权重,所以会被局限在对群体最优经验位置gbest及其周边区域的局部开发中,却没有足够大的速度惯性对此种束缚进行突破。于是,当群体最优经验位置gbest经过一定代数的停滞后,整个种群将密集凝聚在gbest附近,种群多样性急剧下降,逐渐失去发生改变的活力。此时即出现了常见的早熟现象。早熟现象的出现会导致算法收敛精度下降,并造成计算资源的浪费[17-19]。
为使算法的优化效果更好,本文采用IPSO,其权值调整方式如式(10)所示:
(10)
其中:a、b的定义如式(11)所示,
(11)


图9 ITAE目标函数
3.2 ITAE目标函数
本文采用ITAE指标作为粒子群算法的寻优目标,将其在Simulink中封装成子模块,如图9所示。ITAE指标是一种实用性很强的指标,它能够综合评价控制系统的动态和静态性能,在实际工程中有着广泛的应用[20]。其可表示为:

(12)
3.3 比例因子、量化因子的优化
选取种群规模为50,维度为4,位置取[0,1],速度取[-0.1,0.1],取c1=c2=2。在MATLAB脚本文件中编写算法程序,目标函数的适应度值由Simulink中控制系统仿真模型输出。
综上所述,在MATLAB/Simulink中搭建完整的系统控制模块图,如图10所示。

图10 完整控制模块图
4 仿真分析
为了验证上述方法的有效性,采用本文所提出的控制方法控制交错并联双向DC/DC变换器。由于Buck模式和Boost模式仿真结果基本一致,对Buck模式进行仿真分析。变换器及仿真主要参数如表2所示。

表2 变换器参数表
在MATLAB/Simulink环境下进行仿真分析,得到的仿真结果如图11所示。

(a) 输出电压对比图
图11a为两种控制方法的输出电压对比图。由图11a可知:相比于模糊PI控制,IPSO模糊PI控制下的变换器输出电压上升时间快了约1 ms,峰值时间快了约2 ms,超调量降低了约7.5%,稳态时间快了约7 ms。表明其上升更快,超调量更小,且达到稳态时间更短。图11b为t=0.02 s时并联20 Ω负载的输出电压对比图。由图11b可知:相比于模糊PI控制,采用IPSO模糊PI控制时,电压波动减小了约53 V,恢复时间快了约10 ms。说明IPSO优化下的模糊PI控制器动态响应速度更快、稳定性能更好。图11c为t=0.02 s时,参考电压由200 V跃变至300 V输出电压对比图。由图11c可以看出:当参考电压跃变时,IPSO优化下的模糊PI输出电压基本没有波动,而传统的模糊PI电压波动很大;IPSO优化下的模糊PI从参考电压开始跃变到恢复稳态大约经历约6 ms,而模糊PI历时约15 ms,IPSO模糊PI较之快了大约9 ms。这充分表明:IPSO优化的模糊PI在动态性能方面明显优于传统的模糊PI。
5 结束语
由于双向DC/DC变换器在传统的模糊PI控制中,动态效果较差。本文提出了一种改进粒子群算法优化的交错并联双向DC/DC变换器模糊PI控制方法。首先,采用电压电流双闭环方法控制变换器。然后,对双闭环控制的电压外环施加模糊控制,使得PI控制器的参数能够实时调整。最后,运用IPSO优化模糊控制中的量化因子和比例因子。实验结果表明:该算法优化下的模糊PI控制方法有效加快了变换器的响应速度,减小了超调量;并且,当负载变化时或者参考电压变化时,加快了输出电压恢复到稳态的速度。

