基于因果图模型应用调整集估计数据的因果效应

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

SAS/STAT中的PROC CAUSALGRAPH过程为因果图过程［1］，该过程可以在不提供数据的前提条件下，基于设定的因果图模型进行统计推断。该过程有5个局限性：①因果图过程不能处理有向循环的因果图模型；②因果图过程不能评估动态处理方案；③因果效应识别是一个总体概念；④因果效应识别是一个非参数概念；⑤因果图过程不能识别某些因果图模型中的因果效应。本文在介绍因果图过程的局限性之后，针对一个实例并借助SAS软件，实现基于因果图模型应用调整集估计数据的因果效应。

1 因果图过程的局限性

1.1 不能处理有向循环的因果图模型

因果图过程分析代表因果图模型的有向无环图（Directed acyclic graphs，DAG），这些DAG不能包含有向循环。在两个变量（直接或间接）相互导致的情况下，基于DAG的因果图过程分析可能存在困难。对于这种情况，一种常见的方法是引入额外的变量，以便在更精确的时间尺度上描述数据生成过程［2-3］。

1.2 不能评估动态处理方案

因果图过程使研究者能够在识别分析中指定多个处理变量和结果变量。当指定多个处理变量时，因果效应被解释为联合因果效应。也就是说，因果效应被解释为同时对所有处理变量施加特定值的假设结果，研究者还可以将多个处理变量解释为顺序处理行动，前提是处理顺序是预先确定的［2］。然而，研究者不能使用因果图过程来评估动态处理方案的可识别性。

当研究者指定多个结果变量时，每个结果都被单独解释为一个独特的因果效应。虽然解释是独立的，但因果图过程只构建对每个结果变量有效的调整集。在某些情况下，可能不存在此类的调整集，即使可以分别确定对每个结果的因果效应。例如，如果X对Y1的因果效应只能通过调整集Z1识别，而X对Y2的因果效应只能通过调整集Z2识别，其中，Z1和Z2是两个不相交集，则不存在同时对两个结果变量有效的调整集。

1.3 因果效应识别是一个总体概念

根据观测数据估计的因果效应没有有效的因果解释，除非这些数据以因果图模型的形式得到一组因果假设的补充［4］。然而，因果图模型代表了在总体水平上变量之间的假设关系，而不是在个体水平上。因此，使用DAG描述因果效应识别的理论不考虑取样变异性，识别条件在渐近极限下有效（随着观察次数的增加）［2］。成功的识别策略（使用调整集或条件工具变量）是使用非随机试验数据估计因果效应的第一步［5］。研究者应仔细考虑取样变异在估计因果效应和检验模型的显著性时的作用。

1.4 因果效应识别是一个非参数概念

因果效应的可识别性是一个完全非参数的概念，因为它不依赖于因果模型中变量和边的分布或函数形式。然而，识别策略以及由该策略计算的任何估计值应被理解为以假设因果模型的有效性为条件［2］。此外，当因果效应被证明是确定的（例如使用调整集），这并不意味着研究者可以自由选择一个参数估计器来量化效应，参数估计的适用性取决于参数假设，这些假设与因果图模型的假设是分开的，必须针对每个具体情况进行证明［6］。

1.5 不能识别某些因果图模型中的因果效应

在实践中，常出现不能识别某些因果图模型中的因果效应的情况。当在特定的因果图模型中无法确定因果效应时，可采取一些补救措施：①研究者可以修改因果图模型的假设，以查看数据生成过程是否可以由替代模型进行描述；②研究者可以考虑观测其他变量，可能采取的形式是为以前未测量的变量添加观测值，或为现有模型添加新变量和边［4］，然而，在现有的一组变量中添加边对识别因果关系不仅没有帮助，甚至可能有害［4-5］。

2 应用调整集估计数据的因果效应

2.1 问题与背景信息

【例1】沿用文献［1］中“Example 34.3”的问题和背景信息，模型中对处理变量尿酸盐（Urate）和结果变量心血管疾病（CVD）进行了阴影处理。假设变量营养（Nutrition）对应于潜在结构，故不进行测量。还假设变量先前高密度脂蛋白（PreviousHDL）为未测量变量。研究者设定变量之间的关系如图1所示［6］。试使用因果图过程来估计具备有效因果解释的因果效应的大小。

图1 血清尿酸盐对心血管疾病风险影响的因果图模型Figure 1 Causal graph model of the effect of serum urate on risk of cardiovascular disease

2.2 分析因果图模型的思路

2.2.1 基本方法

要从数据集估计具备有效因果解释的因果效应，可使用以下方法：①仔细考虑数据生成过程，并创建一个因果假设列表，以准确表示该过程，在因果图模型中对这些假设进行编码；②使用此图形模型查找有效的识别策略；③利用识别结果构造一个估计量，如分层估计量。

在大多数实际情况下，真正的数据生成过程并不明确。研究者必须定义一个假设，并用因果图模型来呈现。要构建这个因果图模型，研究者可以依据专家意见、已建立的科学理论、先前的经验或其他可靠的知识来源。

2.2.2 产生模拟数据集

以下数据步创建了一个与图1中的模型一致的模拟数据集，并定义了真正的数据生成过程。设所需要的SAS程序如下：

【SAS输出结果及解释】

模拟数据集的前10行见表1。

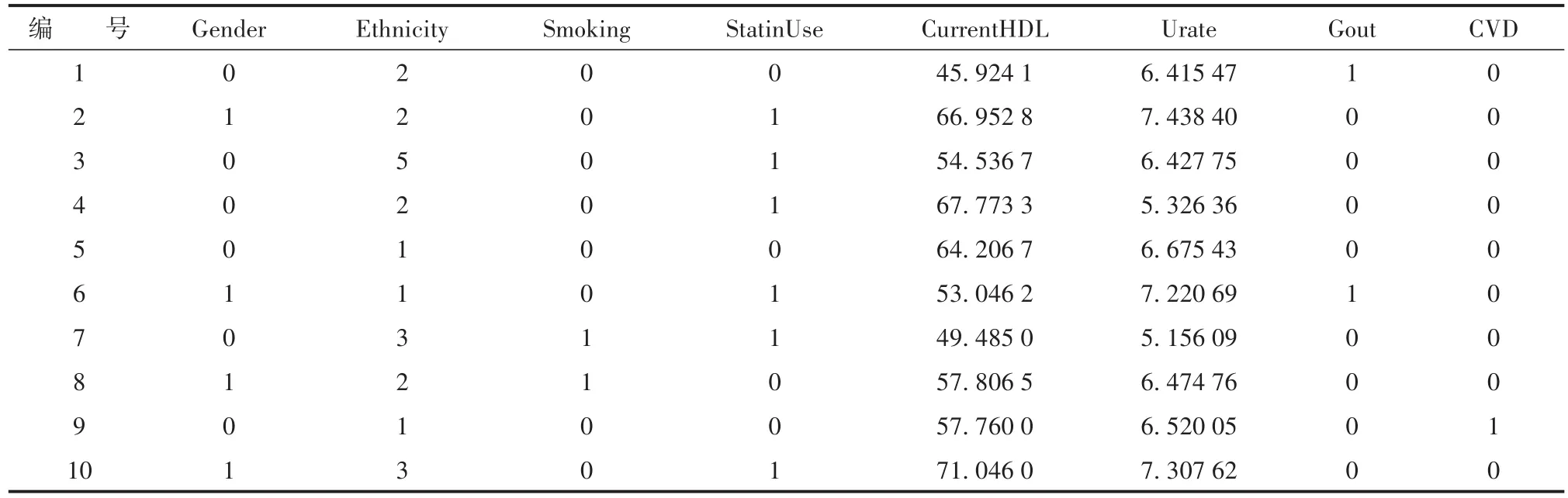
表1 模拟数据集的前10行Table 1 The first 10 lines of the simulated data set

2.2.3 输出Urate的汇总统计量

使用模拟数据集创建Urate的汇总统计量。设所需要的SAS程序如下：

proc means data=CVDdata；

var Urate；

ods output Summary=SampleMeansOutput；

run；

【SAS输出结果及解释】

汇总统计量如表2所示。研究者可以使用ODS OUTPUT语句将变量Urate的汇总统计量存储在输出数据集中。在后面的分析中，研究者将使用此信息来定义感兴趣的因果效应的处理和对照水平。

表2 Urate的汇总统计量Table 2 Summary statistics for urate

2.3 找出模型中可能的调整集

2.3.1 基本情况

在此例中，处理或暴露变量Urate是连续的。此外，该变量对中介变量痛风（Gout）和结果变量CVD的影响是非线性的。因为Urate没有天然的处理和对照水平，所以研究者必须以某种方式定义感兴趣的因果关系。常见的因果效应度量是平均处理效应或预期风险差异，即明确定义的处理和对照条件或水平之间的预期潜在结果值的差异。

在本例中，研究者认为感兴趣的因果关系是CVD的预期风险差异，该风险差异与Urate从对照状态变为处理状态有关。这里考虑了定义对照和处理条件的两种可能性。通过这种方式，研究者可以探索因果效应的大小如何取决于所考虑的处理变量的值。

首先，考虑Urate单位变化的因果效应，以总体平均值为中心。然后，在潜在结果表示法中，感兴趣的因果效应是预期风险差异，见式（1）：

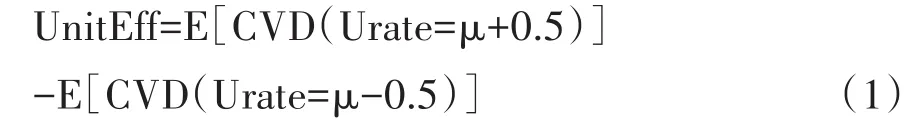
式（1）中，μ是Urate的总体平均值。在因果关系定义中，对照条件定义为低于总体平均Urate的半个单位，处理条件定义为高于总体平均Urate的半个单位。其次，考虑Urate中一个标准差变化的因果效应，也以总体平均值为中心。因果效应现在定义为预期风险差异，见式（2）：

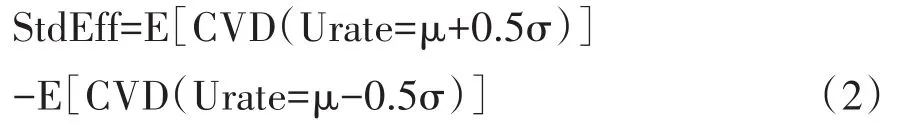
式（2）中，σ是Urate的总体标准差。

根据前面提到的真实数据生成过程，通过生成大量潜在结果（100 000 000次重复）来计算两个群体因果效应。通过该方法，总体效应UnitEff为0.007 6，标准化总体效应StdEff为0.006 8。这些值是研究者根据随机样本估计的目标因果效应。

2.3.2 列出可用于识别因果效应的调整集

给定数据的因果图模型，研究者可以使用因果图过程分析变量Urate对CVD因果效应的可识别性。以下程序使用该过程列出可用于识别此因果效应的有效调整集。为简洁起见，使用MAXSIZE=2选项仅构造不超过两个元素的调整集。设所需要的SAS程序如下：

【SAS输出结果及解释】

该例产生的调整集列表如表3所示。

表3 模型中可能的调整集Table 3 Possible adjustment sets for the model

【表3中有关内容的说明】第2列的“大小”指协变量的个数（各行均有2个）；第3列的“最小”指所找到的调整集是否为最小的调整集（各行上的调整集包含2个协变量，均为最小的调整集）。

请注意，表3中不显示空集。这意味着变量Urate和CVD之间的边际关联不能用来估计具备有效因果解释的因果效应。相反，研究者必须使用另一种估算策略，例如，使用表3中的一个调整集的逐步调整估算。如本例后面的内容所示，未能执行此类调整会导致对因果效应的有偏估计。

研究者可以使用表3中的任何调整集来获得变量Urate对CVD影响的估计，该估计具备有效的因果解释。集合｛Smoking，StatinUse｝是一个有效的调整集，它还有一个特性，即集合中的两个变量都是二值分类变量。因此，估计因果效应的一种可能方法是根据这两个变量的水平进行分层分析。

2.4 平均处理效应或预期风险差异

2.4.1 基本情况

目前正在估计两种因果效应。一个是Urate对CVD的未标准化单位效应，表示为UnitEff，另一个是Urate对CVD的标准化单位效应，表示为StdEff。这两种因果效应都是根据预期CVD潜在结果值的差异来定义的，在某些Urate处理和对照水平上评估这些潜在结果，这些处理和对照水平是根据总体参数定义的。由于这些总体参数以及处理和对照水平未知，故需要从样本中估计它们。

2.4.2 计算处理水平与对照水平的样本值

下面的程序从本例前面创建的汇总统计表中计算Urate处理和对照水平的两组样本值。这些计算值存储在数据集ScoreData中，研究者将使用该数据集来估计两个因果效应。设所需要的SAS程序如下：

以下程序执行Logistic回归分析，该分析按因果图过程结果建议的两个调整变量的水平分层：

【SAS输出解释】

因篇幅所限，具体的输出结果从略。现对其主要内容概要解说如下：

在上述两个二值调整变量“｛Smoking，StatinUse｝”产生的4个层中进行了分析。在每个层中，可以通过UnitTreat和UnitControl之间的P_1差值计算未标准化单位效应，也可以通过StdTreat和StdControl之间的P_1差值计算标准化效应。然而，层内的这些效应都不是因果效应估计值本身。必须使用层中UnitTreat和UnitControl之间P_1差值的加权平均值来计算因果效应UnitEff的估计值，其中，权重是层的样本量。同样，必须使用层中StdTreat和StdControl之间P_1差值的加权平均值来计算因果效应StdEff的估计值（注意：后文中表5中的分层估计列显示了因果效应的这些估计）。

如前所述，如果研究者使用两个变量之间的边际关联（即未调整）来估计变量Urate对CVD的效应，那么混杂的协变量会使估计结果产生偏差。严格地说，为了呈现这种有偏差的结果，以下PROC LOGISTIC过程步执行不按任何协变量分层的Logistic回归分析。设所需要的SAS程序如下：

proc logistic data=CVDdata noprint；

model CVD（event='1'）=Urate；

score data=ScoreData out=ProbNaive；

run；

【SAS输出结果及解释】

预期CVD值的相应估计值如表4所示。

表4 未调整的后验概率Table 4 Unadjusted posterior probabilities

由表4可知，研究者有两组估计结果。一组结果是通过使用处理变量和结果变量之间的原始边际关联来计算的（见表4前两行）；另一组结果是基于调整策略的分层估计器计算的（见表4后两行）。

两个估计器计算的因果效应UnitEff和StdEff的估计值如表5所示。

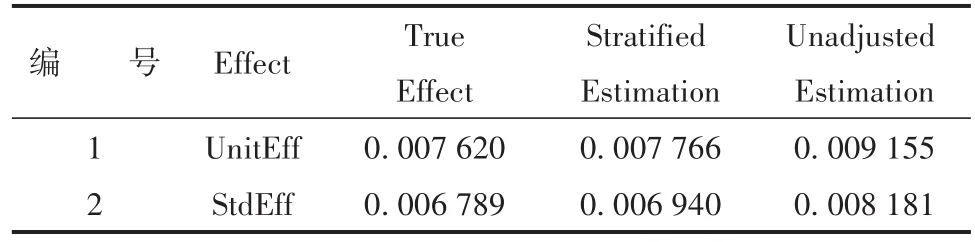
表5 因果效应估计的汇总Table 5 Causa effect estimation summary

由表5可知，使用分层估计计算的估计值（Stratified Estimation）非常接近真实值（True Effect）。因为集合｛Smoking，StatinUse｝是图1所示数据生成过程的有效调整集（见前文表3最后一行）。然而，基于未经调整的原始数据，使用Logistic回归分析得到的估计值（Unadjusted Estimation）与True Effect不一致。因为基于因果图模型分析的结果（见前文表3）表明，空集（指Logistic回归模型中未列入任何协变量）不是有效的调整集。因此，这个例子表明，因果图理论可以在混淆情况下识别因果效应；通过设计因果效应的分层估计，该例还展示了如何基于因果图过程的识别结果实施良好的统计估计策略。

3 讨论与小结

3.1 讨论

采用多重回归分析方法处理资料的前提是研究者已经收集了各变量的具体数据［7-8］，而采用因果图过程进行分析时，不需要提供各变量的具体数据，只需要研究者依据基本常识、专业知识和以往的研究经验对各变量之间的关系作出比较合理的设定，并将其呈现在因果图上。由此可知，科学合理地运用因果图过程，有助于探索出多因素研究课题中可能存在的协变量集合，从而为多因素多指标的研究课题的科研设计奠定良好基础。

3.2 小结

本文介绍了因果图过程的5个局限性，包括：①因果图过程不能处理有向循环的因果图模型；②因果图过程不能评估动态处理方案；③因果效应识别是一个总体概念；④因果效应识别是一个非参数概念；⑤因果图过程不能识别某些因果图模型中的因果效应。同时，本文针对一个实例并基于SAS软件，实现了用调整集估计数据的因果效应的目的。