引入空载电压增益补偿的微网非同型逆变器协同控制

林燎源， 戴宇杰， 朱铠， 项雷军

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

微网技术的快速发展与应用，充分发挥了分布式发电系统的效能.众多位置分散、形式多样、特性各异的分布式能源一般通过逆变装置接入交流微网，给系统运行管理带来挑战.作为典型的逆变器协同控制方法[1]，下垂控制能够实现多逆变器无信号内联线并联运行，成为近年来的研究热点.目前，基于下垂控制的逆变器并联技术已有较多的研究，主要集中于功率调度精度提升[2]、动态性能增强[3]、电压不平衡补偿[4]和经济运行[5]等方面.

基于下垂控制的逆变器并联系统经常面临阻抗失配问题.虚拟阻抗法是解决由阻抗失配引起的负荷分配问题的一个主要思路[6].该方法需要针对不同类型的阻抗进行设计.文献[7]提出带有电压补偿环节的虚拟阻抗法，在功率按容量分配的同时，不会使电压大幅跌落.文献[8] 提出二维虚拟阻抗整定方案，分别调节虚拟电阻和虚拟电感，从而实现基波和谐波的功率均分.文献[9]引入虚拟复阻抗，对逆变器等效输出阻抗进行调节，使其在工频下呈阻性和感性，改善了下垂控制的功率解耦控制性能.改进下垂控制方程是解决由阻抗失配引起的负荷分配问题的另一个思路.借鉴频率下垂控制的误差调节原理，将公共负载电压作为全局量，对电压下垂方程进行改进[10]，可消除功率调度误差.文献[11]在每次负荷变化时，对电压下垂系数进行调整，在无通信条件下，逐渐改善了系统无功均分精度.文献[12]基于有功误差计算积分跟随项，补偿阻性下垂控制中的输出参考电压，实现有功负荷的精确分配.

逆变器的特征可通过电路(拓扑、功率等级、滤波参数和开关频率)和控制(电压控制策略)两个层面进行描述.同型逆变器指各逆变器在电路和控制两个层面均一致，非同型逆变器则指各逆变器至少在某一方面存在较为明显的区别.现有文献大多以同型逆变器并联系统为研究对象，但所提方案若直接应用于非同型逆变器并联控制，则难以获得良好的性能.基于此，本文提出一种基于逆变器空载电压增益补偿的改进下垂控制策略和虚拟阻抗法，补偿逆变器在空载电压增益和等效输出阻抗方面的失配，提高微网非同型逆变器并联系统的稳态功率均分精度.

1 非同型逆变器特性差异分析

1.1 逆变器的特性参数

以单相全桥逆变器为例，逆变器电压控制框图，如图1所示.图1中：逆变器n(n=1，2，…)采用典型的电容电压和电感电流双环控制结构，GV，c，n(s)，GI，c，n(s)分别为电压环调节器和电流环调节器；Ln，Cn分别为输出滤波电感和电容；Re，n为等效串联电阻；Vdc，n为直流电压；Vo，n为输出电容电压；IL，n为电感电流；Io，n为输出电流；Vref，n为参考电压；kf，n为输出电流前馈系数.

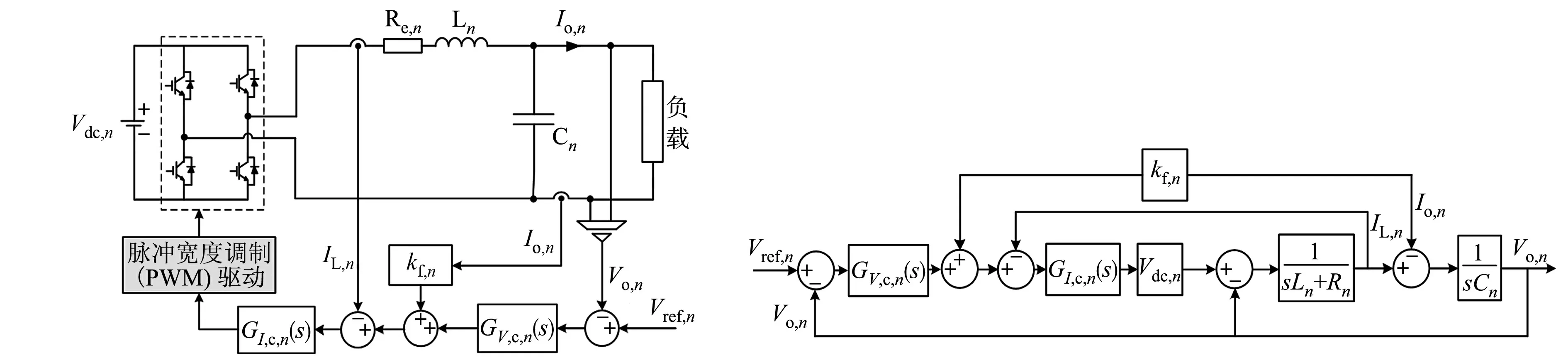
图1 逆变器电压控制框图 图2 逆变器的等效控制框图Fig.1 Voltage control block diagram of inverters Fig.2 Equivalent control block diagram of inverters

由图1可得逆变器的等效控制框图，如图2所示.进而计算逆变器的戴维南等效模型，有

Vo，n(s)=Gc，n(s)Vref，n-Zo，n(s)Io，n，

(1)

(2)

(3)

式(1)～(3)中：Gc，n(s)为空载电压增益；s为拉普拉斯变换因子；Zo，n(s)为等效输出阻抗.

从戴维南等效模型的角度来看，逆变器包含空载电压增益和等效输出阻抗两个特性参数.空载电压增益描述了输出电压跟踪给定参考电压的能力；等效输出阻抗描述了输出电压应对负载扰动时的性能.这两个特性参数均与电压控制策略及参数密切相关.

进一步计算逆变器在基波频率f0=50 Hz处的空载电压增益(空载电压增益的幅值为Kn，相位角为αn)和等效输出阻抗(等效输出阻抗的幅值为Zo，A，n，相位角为βn)，有

(4)

根据式(2)～(4)，可得各逆变器在基波频率处的空载电压增益和等效输出阻抗.

1.2 逆变器特性差异分析

考虑3台单相全桥逆变器(n=1，2，3)组成的并联系统，逆变器1～3采用图1的电压控制策略，3台逆变器采用不同的电压环调节器(GV，c，1～GV，c，3)和电流环调节器(GI，c，1～GI，c，3). 逆变器1的电压环采用准比例谐振(PR)控制器，电流环采用比例积分(PI)控制器；逆变器2的电压环采用PI控制器，电流环采用比例控制；逆变器3的电压环、电流环都采用PI控制器.为减小PI控制下逆变器的等效输出阻抗，逆变器2，3引入不同的输出电流前馈系数kf.

各逆变器环路控制器表达式，如表1所示.表1中：kp为准PR控制器的比例增益系数；kr为积分增益系数；ωc为截止频率；ω0为谐振频率；kV，p，n，kI，p，n分别为电压环和电流环PI控制器的比例系数；kV，i，n，kI，i，n分别为电压环和电流环PI控制器的积分系数.

表1 各逆变器环路控制器表达式Tab.1 Expression of each inverter loop controller

逆变器1的主电路参数为Vdc，1=400 V；L1=5.37 mH；C1=4.72 μF；Re，1=0.05 Ω；逆变器2的主电路参数为Vdc，2=390 V；L2=5.26 mH；C2=4.82 μF；Re，2=0.04 Ω；逆变器3的主电路参数为Vdc，3=380 V；L3=5.12 mH；C3=4.95 μF；Re，3=0.03 Ω.

逆变器1的环路控制参数为kp=0.2，ω0=100π rad·s-1，kr=20，ωc=7.5 rad·s-1，kI，p，1=0.2，kI，i，1=10，kf，1=0；逆变器2的环路控制参数为kV，p，2=0.02，kV，i，2=70，kI，p，2=0.1，kf，2=0.9；逆变器3的环路控制参数为kV，p，3=0.02，kV，i，3=70，kI，p，3=0.2，kI，i，3=10，kf，3=0.8.由于篇幅所限，未给出参数的设计过程.

将各逆变器的主电路参数和环路控制参数代入式(2)～(4)，可以得到基波频率处的特性参数，如表2所示.由表2可知：各逆变器在基波频率处的等效输出阻抗和空载电压增益在幅值和相位角上均存在明显差异.因此，这3台逆变器组成的并联系统为非同型逆变器并联系统.

表2 各逆变器基波频率处的特性参数Tab.2 Characteristic parameters at fundamental frequency for each inverter

2 阻性下垂控制与功率分析

2.1 阻性下垂控制

考虑到在低压微电网中线路阻抗主要呈阻性，故采用阻性下垂控制方程对逆变器输出的有功功率和无功功率进行调节.

阻性下垂控制方程为

Vn=V*-kp，VPn，

(5)

ωn=ω*+kq，ωQn.

(6)

式(5)，(6)中：Vn，ωn为阻性下垂控制方程给出的逆变器n的参考电压的幅值和角频率；kp，V，kq，ω分别为电压和角频率的下垂系数；V*，ω*分别为额定电压的幅值和角频率；Pn，Qn为逆变器n输出的有功功率和无功功率.

根据戴维南等效模型表达式(式(1))，参考电压幅值为Vn，相位角为δn.关注基波频率处的响应，并令功率角φn=αn+δn，有

Gc，n(s)Vref，n|s=j2πf0=KnVn∠(αn+δn)=KnVn∠φn.

(7)

根据式(1)，(7)，可得3台逆变器的并联等效模型，如图3所示.图3中：Io，n为输出电流，此处为向量形式；rn，xn分别为总阻抗(含逆变器等效输出阻抗、馈线阻抗和虚拟阻抗)的阻性成分和感性成分；Vbus为交流母线电压幅值.

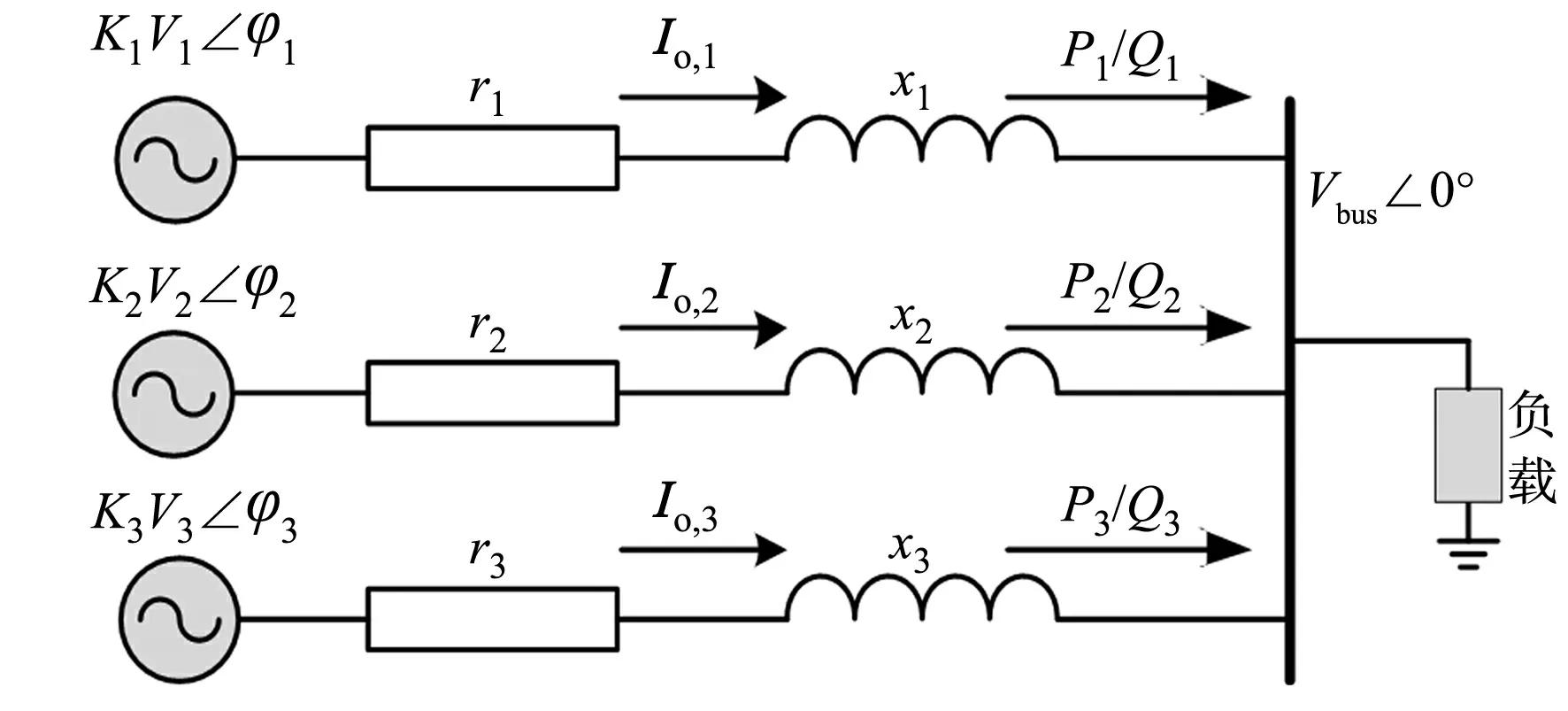
图3 3台逆变器的并联等效模型Fig.3 Parallel equivalent model of three inverters

该并联等效模型的空载电压增益幅值Kn往往不为1且各不相等，使其成为继阻抗参数之外另一个影响并联系统功率均分性能的重要因素.因此，阻性下垂控制直接应用于非同型逆变器并联难以取得良好的功率均分性能.

2.2 功率均分条件

阻性下垂控制稳态时频率的全局性使无功功率能够实现精确调度，不受特性参数差异的影响.因此，对有功功率的均分条件进行分析.

由于图3中的向量用最大值向量表示，故逆变器n流入交流母线的复功率Sn为

(8)

由此可得有功功率和无功功率分别为

(9)

(10)

把式(5)代入式(9)，可得

(11)

把式(11)代入式(5)，可得

(12)

以两台逆变器为例，为了实现P1=P2，电压下垂系数设置为kp，V，1=kp，V，2.根据式(5)，应有电压偏差ΔV=V2-V1=0，将其代入式(12)，可得

(13)

由式(13)可知：由于功率角φ1，φ2存在无数组取值，故存在无数组满足一定关系的K1，K2与等效输出阻抗，使P1=P2成立，逆变器能够在空载电压增益一定时，通过调节阻抗参数实现目标功率输出；同样地，当阻抗参数一定时，也可通过调节空载电压增益达到功率输出一致.

对于非同型逆变器并联系统，若仅调节阻抗参数，难以定量确定应满足的调节方程.因此，需考虑空载电压增益的匹配调节.

3 逆变器空载电压增益补偿

非同型逆变器的等效输出阻抗和空载电压增益存在差异，对功率调度产生影响.此外，采用虚拟阻抗法时，空载电压增益会对虚拟阻抗的实现精度产生影响.因此，引入空载电压增益补偿对下垂控制方程和虚拟阻抗法进行改进.

3.1 下垂控制方程的改进

空载电压增益体现了逆变器输出电压跟踪给定参考电压的能力，而参考电压由下垂控制给出，因此，空载电压增益也是影响均流度的重要因素.非同型逆变器的空载电压增益往往存在差异.通过分析逆变器的输出特性，在阻性下垂控制的基础上，将空载电压增益幅度差异通过电压下垂控制方程补偿到参考电压中.

改进的下垂控制方程为

KnVn=V*-kp，VPn.

(14)

基于式(14)，对于采用不同电压控制策略和参数的逆变器，其戴维南等效模型中电压源的增益幅值Kn将被统一补偿为1，可消除空载电压增益失配对并联系统功率均分的影响.

3.2 虚拟阻抗法的改进

目前，添加虚拟阻抗主要有以下两种方式.

1) 通过改变逆变器的环路控制参数，调节逆变器的等效输出阻抗特性，适应下垂控制策略.

2) 通过引入电流反馈环节调节参考电压，达到模拟实际阻抗的效果.该方式更为常用.

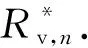
采用虚拟阻抗法时，添加的虚拟阻抗Zv，n为

(15)

式(15)中：Zo，A，n∠βn为逆变器基波频率等效输出阻抗.

虚拟阻抗控制框图，如图4所示.

图4 虚拟阻抗控制框图 图5 改进的虚拟阻抗控制框图 Fig.4 Block diagram of virtual impedance control Fig.5 Block diagram of improved virtual impedance control

此时，逆变器的戴维南等效模型为

Vo，n(s)=Gc，n(s)Vref，n-(Zo，n(s)+Zv，nGc，n(s))Io，n.

(16)

因此，逆变器等效输出阻抗调整为

(17)

由式(17)可知：添加的虚拟阻抗Zv，n的精度将受到空载电压增益幅值和相位角的影响，而非同型逆变器的空载电压增益存在差异，故采用虚拟阻抗法添加虚拟阻抗会额外引入精度差异，降低功率均分的调节效果.

将基波频率f0处的空载电压增益补偿到虚拟阻抗中，改进后的虚拟阻抗控制框图，如图5所示.

添加的虚拟阻抗Zv，n修正为

(18)

由式(18)可得虚拟阻抗Zv，n一般为复阻抗，代入表2的数据，可得3台逆变器需要添加的虚拟阻抗分别为

Zv，1=0.75∠-0.03°，Zv，2=1.03∠-21.78°，Zv，3=1.17∠-46.39°.

借鉴延迟电流法[13]的思想实现虚拟阻抗Zv，n，将Zv，n的幅值乘以延迟Zv，n阻抗角的输出电流，再反馈至参考电压处实现.

由此可得文中方法的非同型逆变器并联整体控制框图，如图6所示.通过引入空载电压增益补偿对阻性下垂控制方程和虚拟阻抗法进行改进，提高非同型逆变器在空载电压增益和等效输出阻抗的匹配，提高系统功率均分精度.

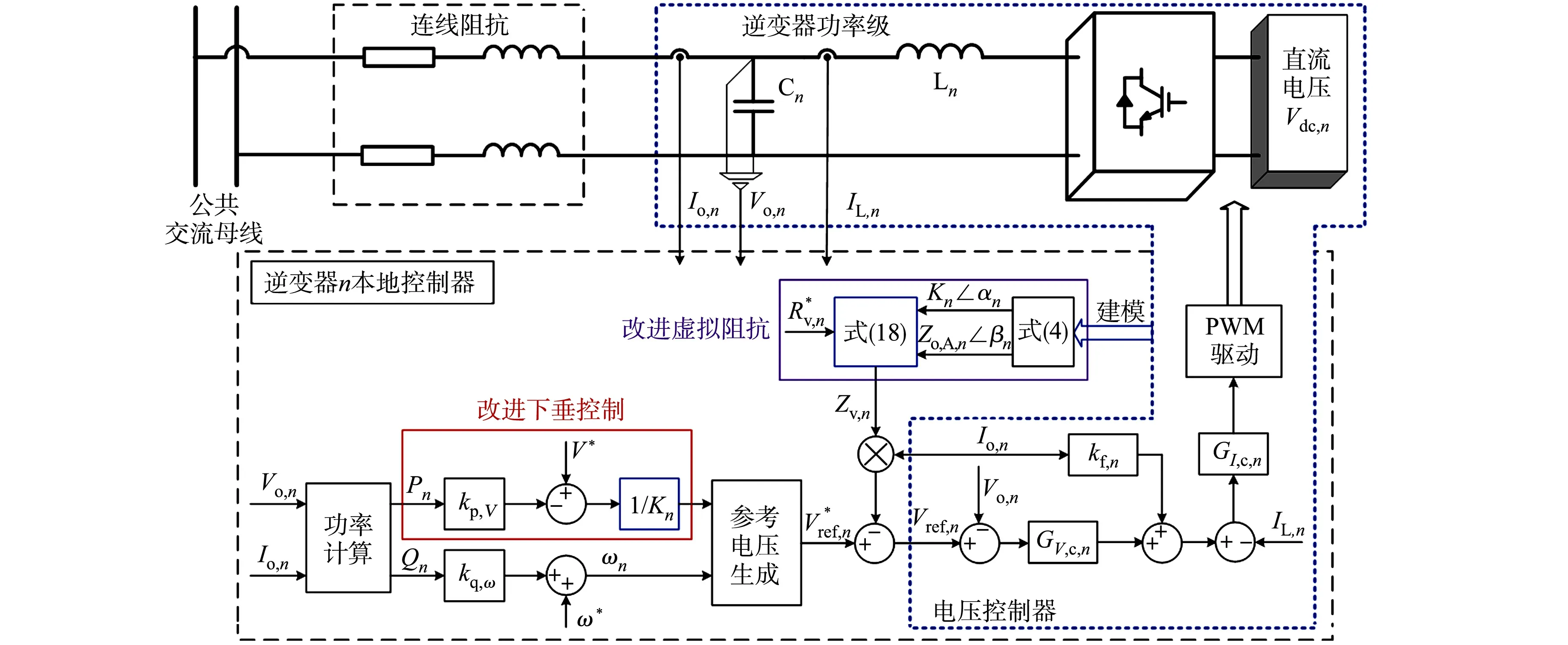
图6 非同型逆变器并联整体控制框图Fig.6 Overall control block diagram of paralleled non-identical inverters

借鉴文献[14]的建模方法，对基于文中方法的并联系统建立小信号状态空间模型，分析系统稳定性及控制参数摄动对系统性能的影响，进而优化控制参数的选取，由于篇幅所限，此部分内容不再赘述.

4 仿真验证

为验证文中方法的性能，在PLECS仿真平台上搭建由3台非同型逆变器构成的微网系统，逆变器控制策略采用文中方法，主电路参数和环路控制参数与上文一致，其他的仿真参数，如表3所示.表3中：rl，1～rl，3分别为逆变器1～3的差异化负载连线阻抗的阻性成分；xl，1～xl，3分别为逆变器1～3的差异化负载连线阻抗的感性成分；Rl为负载电阻；Ll为负载电感；fs为开关频率.仿真开始时，逆变器1先运行，逆变器2，3在0.3 s同时切入并联系统，共同承担负荷.

表3 仿真参数Tab.3 Simulation parameters

采用阻性下垂控制(不添加虚拟阻抗)时，各逆变器的输出功率波形(情况1)，如图7所示.由图7可知：稳态时逆变器1～3的输出有功功率分别为358.2，-152.8，780.3 W，存在明显的均分误差，逆变器2甚至吸收有功功率；当逆变器2，3切入系统时，存在明显的功率过冲和振荡，其中，逆变器2的有功功率和逆变器1的无功功率过冲较大.这是因为3台逆变器的空载电压增益及等效输出阻抗存在差异，匹配程度较差，而稳态时并联系统的频率为全局量，3台逆变器的无功功率能够实现精确均分.

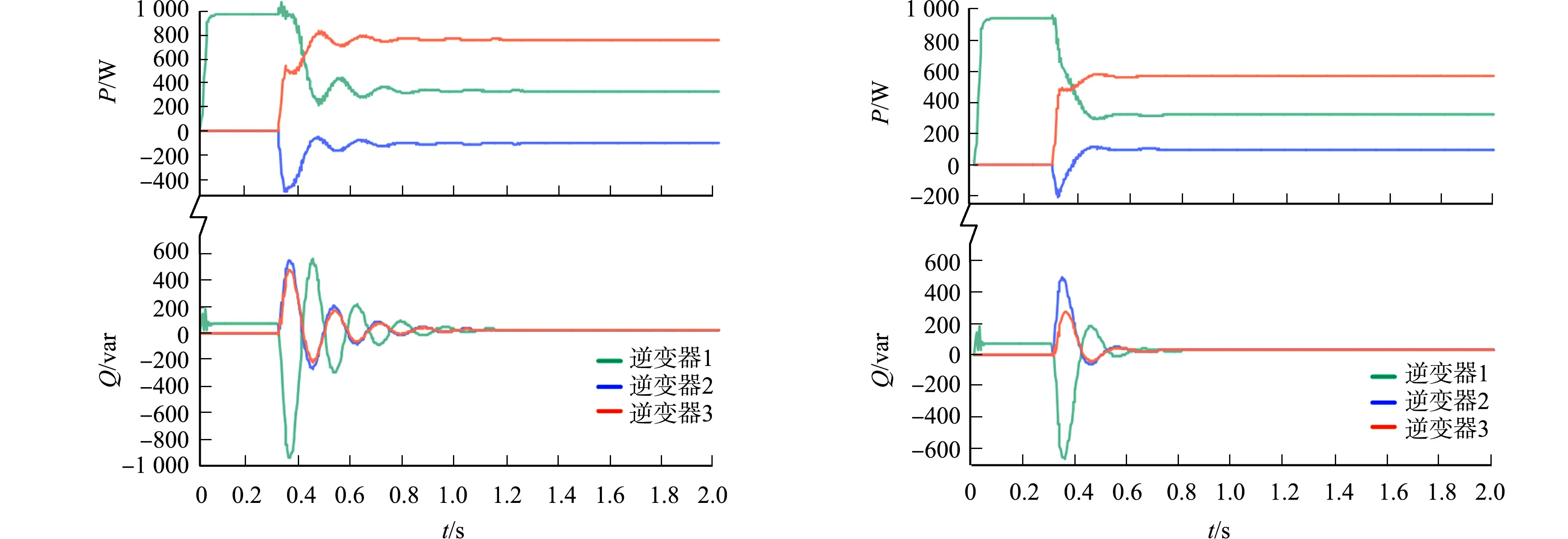
图7 各逆变器的输出功率波形(情况1) 图8 各逆变器的输出功率波形(情况2) Fig.7 Output power waveform of each inverter (situation 1) Fig.8 Output power waveform of each inverter (situation 2)

采用阻性下垂控制与虚拟阻抗法(添加0.8 Ω虚拟电阻)时，各逆变器的输出功率波形(情况2)，如图8所示.由图8可知：稳态时逆变器的1～3的输出有功功率分别为318.4，96.8，567.3 W，有功功率均分精度得到一定程度的提升，逆变器2由吸收有功功率转为发出有功功率；当逆变器2，3切入系统时，功率过冲和振荡得到一定程度的改善，暂态过程时间缩短.这是由于添加的虚拟电阻改善了3台逆变器的等效输出阻抗匹配，但空载电压增益仍存在失配问题，故仍然具有较大的有功功率均分误差.

采用改进的阻性下垂控制和虚拟阻抗法(添加0.8 Ω虚拟电阻)时，各逆变器的输出功率波形(情况3)，如图9所示.由图9可知：稳态时逆变器1～3的输出有功功率分别为310.4，357.1，313.5 W，相较于图8，3台逆变器的有功功率均分精度得到较大提升；当逆变器2切入并联系统时，有功功率过冲得到了有效抑制.这是因为改进下垂控制增强了逆变器的空载电压增益匹配.然而，仍然存在一定的有功功率均分误差，一方面是馈线阻抗存在差异，另一方面是采用虚拟阻抗法添加虚拟电阻的精度受到逆变器空载电压增益不为1的影响.

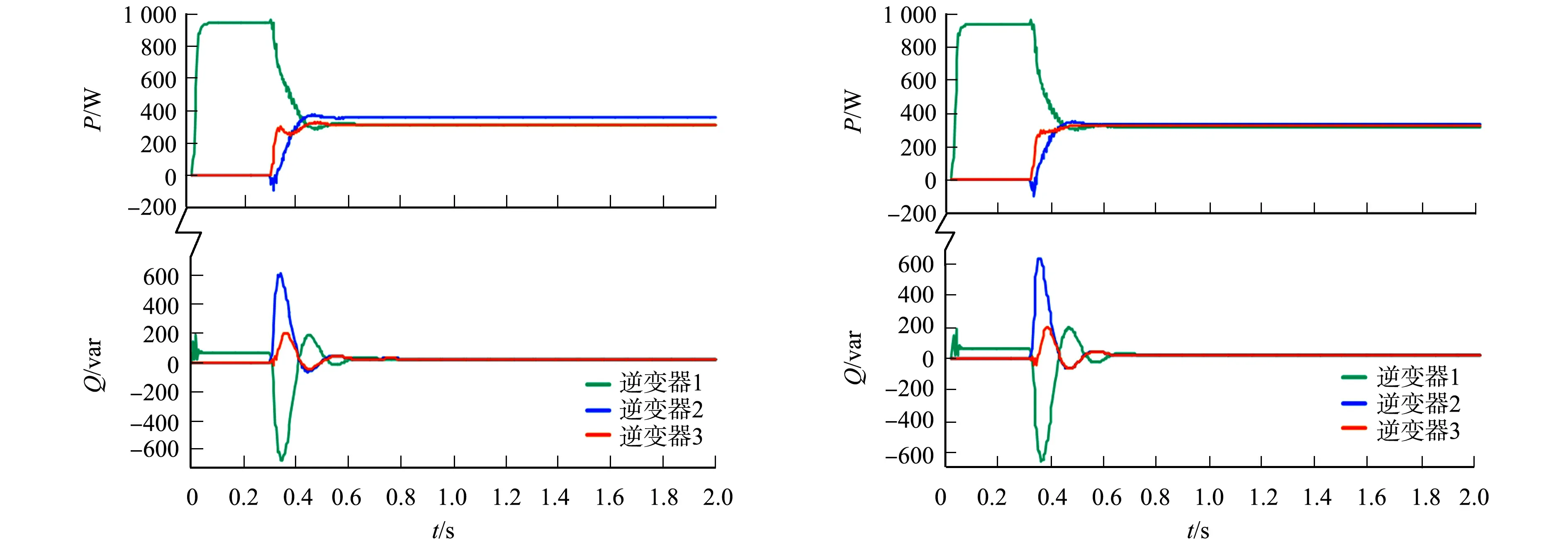
图9 各逆变器的输出功率波形(情况3) 图10 各逆变器的的输出功率波形(情况4) Fig.9 Output power waveform of each inverter (situation 3) Fig.10 Output power waveform of each inverter (situation 4)

采用文中方法时，各逆变器的输出功率波形(情况4)，如图10所示.由图10可知：稳态时的逆变器1～3的输出有功功率分别为321.2，336.1，323.4 W，有功功率基本趋于均分且动态性能良好.这得益于文中方法对非同型逆变器空载电压增益进行补偿，并对虚拟阻抗法进行改进，消除了非同型逆变器不同空载电压增益对虚拟阻抗实现精度的影响.然而，逆变器投入并联系统时的瞬态无功功率过冲和振荡依然存在，今后将进一步研究和优化.

5 结论

以非同型逆变器并联系统为研究对象，提出一种基于空载电压增益补偿的改进下垂控制策略和虚拟阻抗法，通过理论分析与仿真验证了文中方法的有效性，得到以下4个结论.

1) 非同型逆变器协同控制存在等效输出阻抗和空载电压增益两个特性参数的失配问题，两个特性参数均会对输出功率产生影响.

2) 非同型逆变器的空载电压增益参数不同，不同的参数会对虚拟阻抗实现精度产生的影响，进而在一定程度上影响功率均分性能.

3) 逆变器空载电压增益参数的调节匹配能够等效到电压下垂方程中进行.空载电压增益和等效输出阻抗同时调节能够使非同型逆变器并联系统获得良好的稳态功率均分性能.

4) 文中方法能够直接拓展应用于其他类型的下垂控制中.

对于非同型逆变器并联系统，尚存在表征逆变器特征的内部特性参数研究、逆变单元投入系统时的瞬态功率过冲和振荡抑制、不同容量非同型逆变器功率分配、考虑控制延时等因素的系统模型构建及相关实验验证等一系列问题，需要在后续工作中开展进一步的研究.