机载光电稳瞄平台减振技术研究

齐 媛，王惠林，黄维东，曹尹琦，麦玉莹，张向明

（西安应用光学研究所，陕西 西安 710065）

引言

机载光电稳瞄平台主要作用是将光电传感器与其所处环境隔离开来，其环境由安装平台，如：飞机、导弹、舰船或地面车辆的运动决定，使“负载”能够在这一运动环境中瞄准一个给定方向。对于光电稳瞄平台而言，稳定精度是平台功能实现的基础和重要保障[1]，是平台设计研发阶段、生产制造过程以及战场使用过程中的一个重点问题，它直接决定了平台的性能高低[2]。随着未来战争作战半径越来越大，光电传感器作用距离越来越远，对光电稳瞄系统稳定精度提出的要求也越来越高[3-4]，因此稳定精度成为评价光电稳瞄平台设计成败的关键技术指标。

由于机载光电稳瞄平台可能会悬挂于载机的头部、腹部、脊背部或两侧机翼，由载机产生的振动、姿态变化以及大气湍流等都对光电稳瞄平台的视轴稳定性以及跟踪精度造成一定的影响，使视频、图像变得不清晰甚至模糊。一般情况下，为避免载机在运动过程中对成像系统成像质量的影响，通常采用隔振技术提高其稳定精度[5-6]。

对比近几年来国内外光电稳瞄平台的减振技术[7-8]，传统橡胶减振的研究较为火热，相关的技术和产品较为成熟，而国内在光电稳瞄平台柔性减振技术的发展尚属空白[9-15]，文章提出了一种新型柔性隔振设计，代替了传统减振机构，为光电稳瞄平台对高精度需求提出了新的技术支持。

1 减振原理

1.1 传统减振

传统减振设计方法是将整个系统假设为单自由度系统，这个单自由度系统的刚度是由隔振器的弹性体所提供，因为其刚度远远小于其他物理结构。与此同时，整个系统质量一般是选取振源设备和振动敏感结构中较小的那一个。

如图1 所示，图中m代表质量块；k代表线性弹簧刚度；c代表阻尼器的黏滞阻尼系数，F（t）是作用在质量块m上的激励力；x（t）代表质量块m在激励力F（t）作用下的位移。

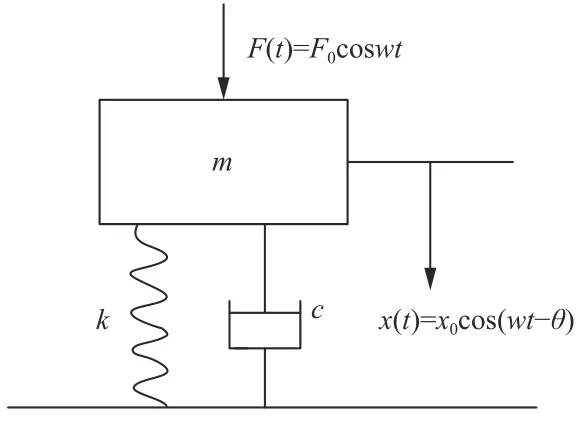
图 1 单自由度振动系统Fig.1 Diagram of single degree of freedom vibration system

根据达朗贝尔原理，可得图1 所示的单自由度线性系统的微分运动方程为

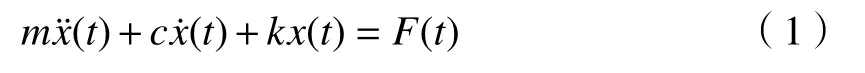
初始条件记为x(t)=Aest

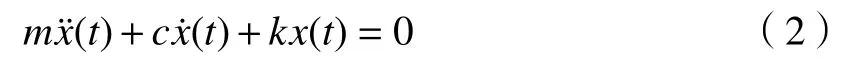
根据常微分方程理论，令，并将其带入（2）式中，得到系统的特征方程：

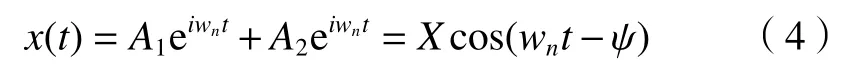
则幅值、频率函数为

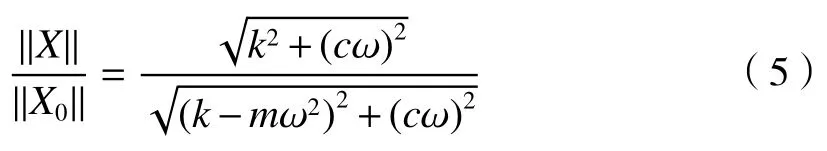
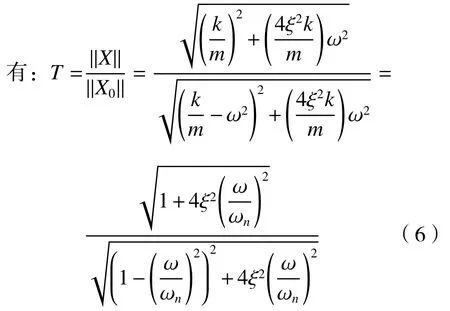
图2（a）中的幅频特性曲线显然具有以下特性：

a)当r=0时，说明振动频率变化很慢，整个系统相当于在平动。

b)当r＞1，且传递率T＜1时，发生共振，且振幅度即共振放大倍数会随着阻尼比越增大而减小。

图2（b）中的相频特性曲线显然具有以下特性：

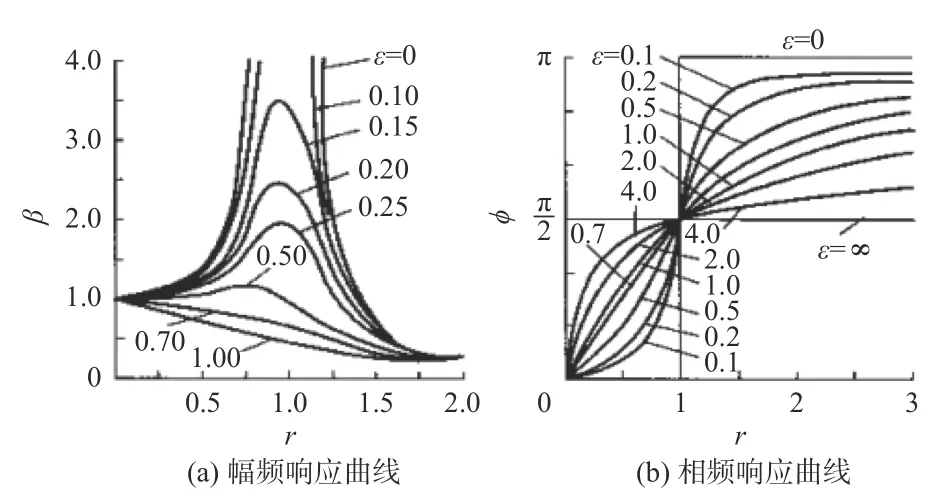
图 2 阻尼比对传递率的影响Fig.2 Effect of damping ratio on transmissibility

a)当w→0时，位移响应与激励f(t)之间几乎是相同的，弹性变形x(t)与作用力f(t)是同相的。

b)当w≫wn时，位移响应与激励f(t)之间是相反的，属于“质量控制区”，因此弹性变形x(t)与作用力f(t)是反相的。

c)当w≈wn时，属于“阻尼控制区”，弹性变形x(t)与作用力f(t)之间有π/2的相位差。

可以看出传统减振器存在以下几点问题，首先，传统减振器在低频和超低频处的隔振性能受限，甚至会放大低频振动；且确定最优阻尼值需要权衡系统的谐振峰值和高频段的衰减，难以兼顾基础振动隔离和直接干扰抑制；结构参数随时间变化会导致系统性能下降；由于系统参数在设定后无法改变，被动控制难以适应干扰频带变化的情况。

1.2 准零刚度减振

针对传统传感器的缺点，对稳定性和隔振性进行综合考虑，引入了负刚度概念，进行了正负刚度耦合减振设计，在避免导致失稳的前提下，降低隔振刚度，甚至可降低至准零刚度，大幅拓展隔振系统的适用性。准零刚度减振器即为动刚度接近于零的减振器，目前常见如下3 种设计形式：

a)将负刚度机构并联到正刚度系统中实现准零刚度。

b)利用特定形状的结构力-形变之间的非线性关系实现准零刚度。

(c)采用全新的隔振机理。

准零刚度减振原理如图3 所示。在缓慢加载（或者逐级加载）的过程中，弹簧节点从C位置向AB移动，位置变化与载荷成单调变化（可以近似看成是线性的）。但在经过AB位置后，即使载荷减小甚至不加载荷，弹簧仍会向O 运动。此时载荷的变化率呈现负值，势能变化率也呈现负值。通常情况下将位移随载荷增大而增大（即从平衡点处开始，势能随垂向位移增大而增大）定义为刚度（或称正刚度），那么图3 中结构载荷变化率呈现负值时就定义为负刚度。由于有负刚度段存在，所以该结构具有负刚度特性。

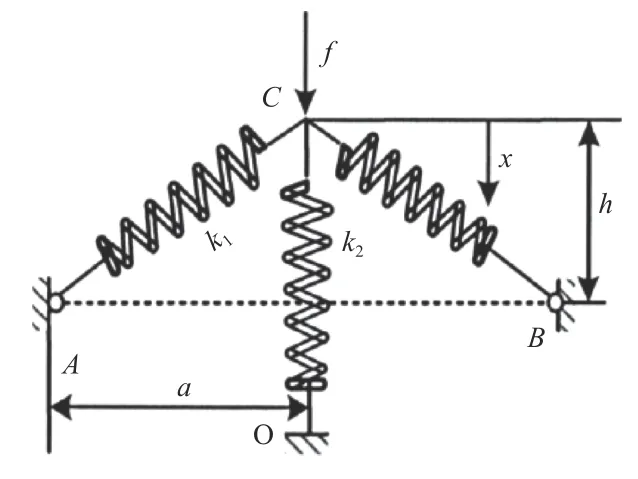
图 3 准零刚度减振原理图Fig.3 Diagram of vibration reduction of quasi-zero stiffness

如图4 所示，准零刚度减振的特点是，该工作状态几乎可以隔绝所有频段扰动，且不会导致系统失稳；参数调整对系统质量没有影响。但也存在一些问题，就是引入了非线性隔振，非线性隔振与线性隔振的最主要区别是，非线性隔振存在不稳定区间（存在不连续跳跃问题），参数匹配时应确保下跳点与上跳点频率重合。

综上所述，目前主要的2 种隔振方式：传统被动隔振技术由于受限于“”因素，只能存在于一些扰动频率较低的应用中，难以在隔振的稳定性与效率上同时取得最优，极大地限制了隔振效果；由于准零刚度隔振技术存在不连续跳跃问题，因此系统设计复杂且不易实现。

2 柔性支撑减振装置组成

针对以上2 种减振技术的特点，提出了一种柔性支撑减振方式。由于传统的机载光电稳瞄平台采用的是橡胶减振器连接外框架和内环万向架，内环万向架采用框架形式，电机和编码器安装在轴端，光学载荷上安装陀螺用于敏感瞄准线抖动。该形式的万向架轴承与电机电刷之间的摩擦力，以及万向架约束结构的共振，限制了光电稳瞄系统的稳定效果。为了减小光电稳瞄系统受周围环境振动的影响，就要保证光学载荷框架具备减振功能，为了减小电机旋转的无效负载，提高系统姿态控制精度，就要保证光学载荷安装在框架内时具有较低的扭转刚度。因此，提出了一种新型柔性减振设计，如图5 所示。通过虚拟万向架将光学载荷“悬挂”于稳定平台上，实现光学载荷的支撑，并将光学载荷与外框架连接；利用柔性支撑隔振体的结构弹性特点，使万向架具备角运动和减振的功能；并且柔性支撑隔振体本身具有阻尼，可实现被动减振。

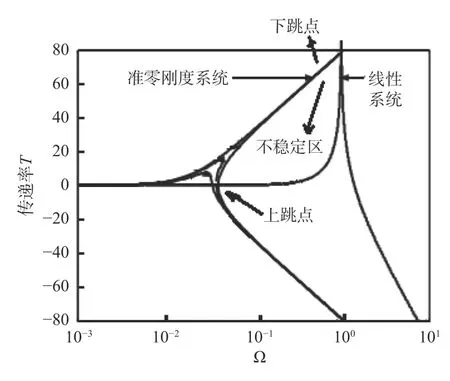
图 4 准零刚度减振器隔振特性图Fig.4 Diagram of vibration isolation characteristics for quasi-zero stiffness absorber

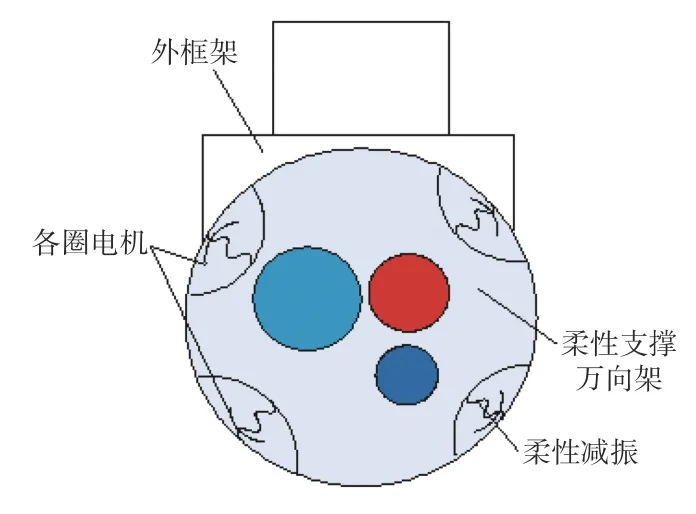
图 5 柔性支撑减振稳瞄平台组成图Fig.5 Composition diagram of flexible support vibration reduction and stabilized sighting platform

2.1 柔性支撑减振刚度分析

提出了一种由8 个柔性支撑件组成的减振结构，该结构的四面体顶角布局形式如图6 所示。图6 中序号1～8 的柔性支撑件放置在四面体的8 个顶点上，每个柔性支撑件由四面体中心点O 向外延伸到每个顶角上，从而形成柔性支撑隔振体两两相对放置的平衡柔性隔离阵，可以是由不同放置形式的柔性支撑隔振体组成。

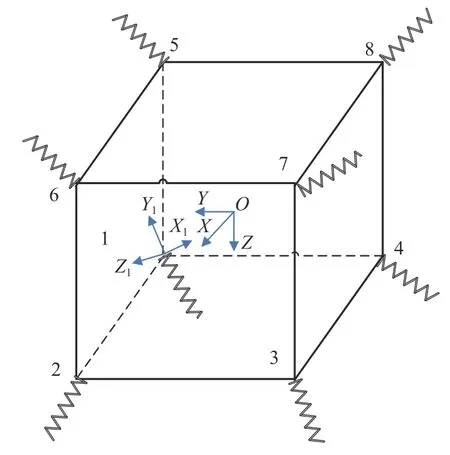
图 6 柔性支撑减振四面体顶角布局图Fig.6 Vertex angle layout of flexible support vibration reduction tetrahedron

由于刚度是标量，是不能被分解的，但是力与位移是矢量，可以被分解，故将柔性支撑减振体各点的位移在不同的坐标系下进行表示。在自身坐标系下求解力，再将力转换到原有坐标系下，将立方体构型进行分析，立方体边长为a，柔性支撑减振体与负载连接点构成的立方体边长b，负载坐标系O-XYZ，负载平移运动(x0,y0,z0)，负载转动运动(α0,β0,γ0)。

负载与框架相对运动引起的柔性支撑减振体位移在坐标系O-XYZ的位移量为

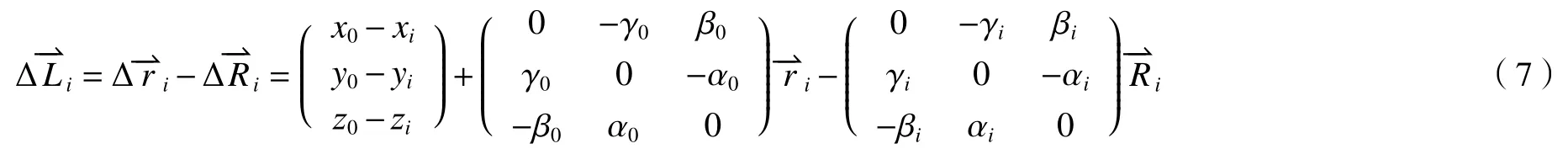
各柔性支撑减振体的结构力在XYZ坐标下表示为

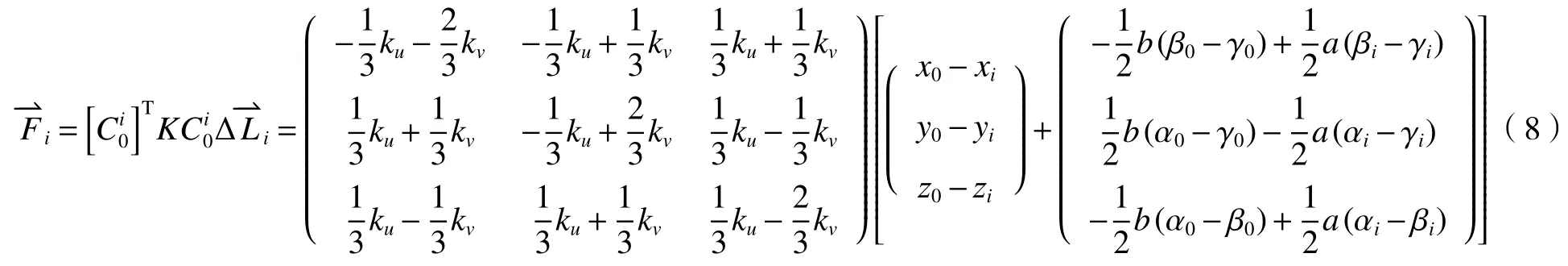
由各柔性支撑减振体产生的扭转力矩表示为

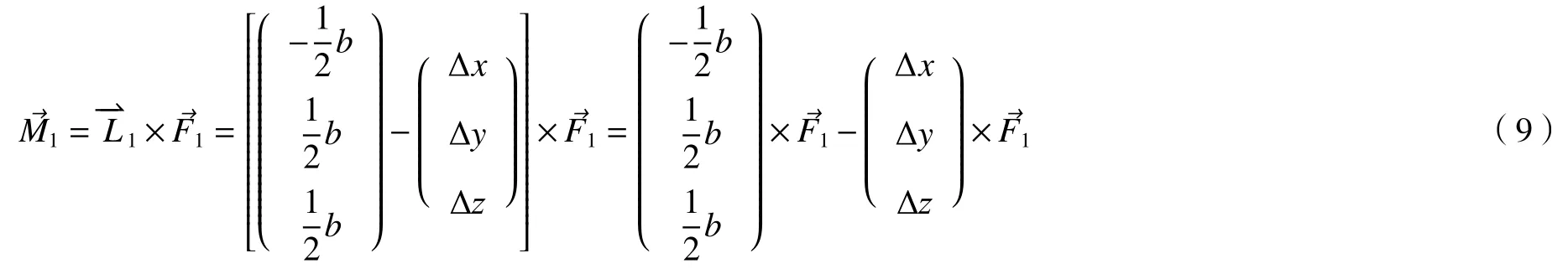
忽略单根柔性支撑体自身位移 Δx、Δy、Δz。则由（9）式可以得到单根柔性减振支撑体在负载下的轴向刚度ku和侧向刚度kv的计算公式为

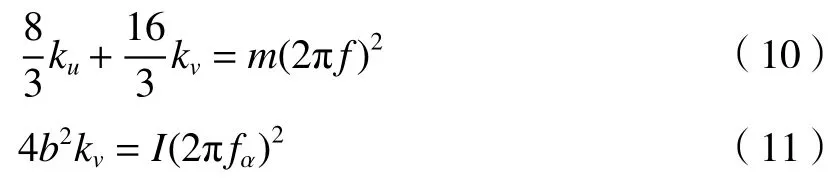
式中：负载质量m=15 kg；转动惯量I=0.3 kgm3；系统平动时无阻尼固有频率f=15 Hz；转动时无阻尼固有频率fa=3 Hz；负载边长b=0.2 m。由此得到柔性支撑体的轴向刚度为ku=49.9 N/mm；柔性支撑体的侧向刚度为kv=0.67 N/mm。

2.2 柔性支撑减振模态分析

减振系统的设计通常与载体振动环境有关，即根据载机的振动功率谱密度曲线，选取减振系统的固有频率。本文以某直升机振动功率谱密度曲线作为振动输入条件，对减振系统的固有频率选取的15 Hz 进行分析。为验证该柔性支撑减振结构的转动和平动的频率，本文采用ANSYS Workbench 仿真软件进行有限元软件仿真检验。分析过程中，首先建立模型如图7 所示，其中负载质量m=15 kg，转动惯量I=0.3 kgm3，8 个柔性体均布于200 mm 的立方体顶角，利用六自由度弹性体bushing 单元设置6 个方向的刚度，设定柔性支撑隔振体的轴向刚度为ku=49.9 N/mm，柔性支撑隔振体的侧向刚度kv=0.67 N/mm，接着对其三维模型进行转化以及网格划分，最后施加边界条件约束，对整个负载进行机械谐振频率的仿真。

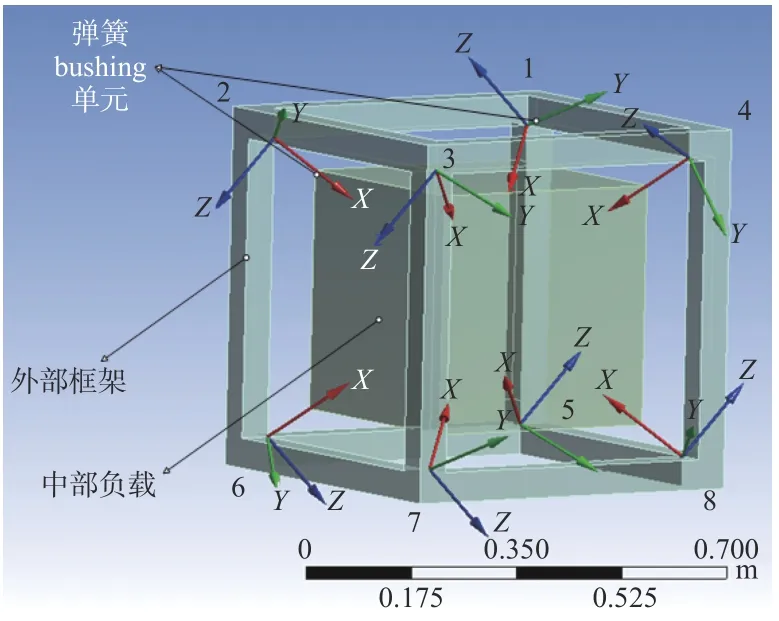
图 7 Bushing 单元模型图Fig.7 Diagram of Bushing unit model

根据上述程序所计算出来的系统，具有6 个模态，其中前3 阶为转动，后3 阶为平动。结果如图8（a）～图8（f）所示。系统平动时无阻尼固有频率f=15 Hz，转动时无阻尼固有频率fa=3.7 Hz。可以看出，柔性支撑隔振结构对机载光电稳瞄平台提供高频隔振以及静态支撑功能，进而提升光电稳瞄平台的稳定性和抗干扰能力。

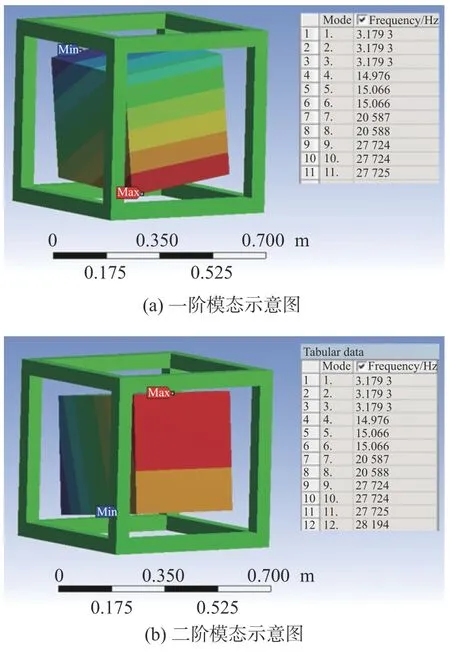
图 8 六阶模态示意图Fig.8 Schematic diagram of sixth-order mode

3 实验结果与分析

3.1 振动试验

在实际工作过程中，柔性支撑隔振测试结构会受到载体平台、外界环境等因素影响而产生振动。为检测该测试结构在振动工作环境下的稳定性能，对工作方向进行振动实验。本文以某直升机振动功率谱密度曲线作为振动输入条件，将整个测试结构放在振动台上，调节弹簧柔性体组件的压缩量（预紧力），利用加速度计读出系统的平动频率，测试实验如图9 所示。

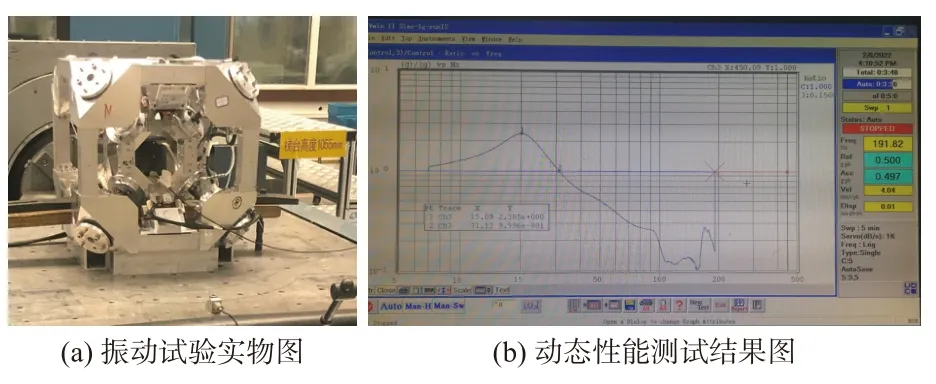
图 9 振动试验结果Fig.9 Diagram of vibration test results

如图9（a）所示，调节弹簧柔性减振装置的压缩量，负载15 kg 时，该测试平台的平动频率为15 Hz；从图9（b）的曲线结果可以看出，测试装置在中低频对振动起到了有效的隔振，且谐振点处的放大倍率较小，高频处也有明显的衰减作用。

3.2 实验结果与讨论

在柔性支撑隔振结构的无阻尼被动隔振的基础上，与主动阻尼控制隔振相结合，如图10 所示。主动阻尼控制系统主要响应柔性支撑隔振测试结构在谐振频率附近的频率，主动阻尼减振控制衰减了无阻尼被动减振的振动峰值，可见对中低频起到了有效的隔振效果。而相对于被动阻尼减振（传统橡胶减振器），这种混合隔振（主动阻尼/无阻尼被动隔振）同时也对高频起到了一定的衰减作用。

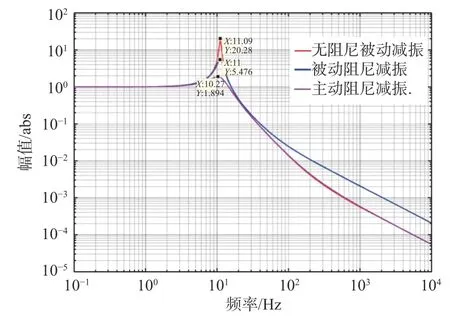
图 10 柔性支撑隔振性能对比Fig.10 Comparison of vibration isolation performance of flexible support

4 结论

本文提出了一种适用于光电稳瞄平台的柔性支撑减振方式，相较于传统橡胶减振器以及准零刚度减振器，对机载光电稳瞄平台低频产生了有效的隔振，同时也对高频起到了一定的衰减作用，可实现对光电稳瞄平台稳定精度的提升。在此基础上，利用ANSYS 仿真软件对其模态进行仿真分析，可以看出柔性支撑隔振结构对机载光电稳瞄平台提供了高频隔振以及静态支撑功能。最后，建立了柔性支撑隔振测试装置，测试其在动态环境下的稳定性，测试结果与仿真评估误差为0.56%，验证了该减振结构设计的有效性。