基于Lasso回归模型的青岛海洋经济和海洋产业分析
张贺,范梦萱
(中国海洋大学 青岛 266000)
0 引言
我国是海洋大国,海洋资源极为丰富。随着海洋开发利用日益受到重视,推动海洋经济发展已成为全国共识。在建设海洋强国的背景下,实现海洋经济高质量发展和完成海洋产业转型升级对青岛整体经济的发展具有重要意义。
依海而生,向海图强。青岛地处山东东南沿海的丘陵地带,不适合发展大型机械化种植业;由于三面环海,海洋产业一直是青岛经济发展的重要组成部分,“蓝色硅谷”、西海岸新区和红岛经济区等建设对青岛海洋经济发展的引领作用日益显现[1]。2021年上半年青岛海洋生产总值增长21.9%,占GDP比重为32%,海洋第一产业、第二产业和第三产业分别增长7.7%、19.7%和25.2%。目前青岛发展海洋经济的优势突出体现在产业体系完整、产业集群众多、基本实现产业全面覆盖、科研机构云集和港口辐射能力强,尤其在海水养殖业和滨海旅游业方面具有得天独厚的优势。
已有学者采用多部门经济模型测度不同变量对海洋生产总值的贡献度,如王端岚[2]研究福建海洋产业结构变化对海洋经济增长的促进作用,并提出海洋生态环境保护和资源可持续利用的重要价值。格兰杰因果方法在海洋产业结构和海洋经济发展的研究方面也有应用,结果表明二者具有相互促进的关系。部分学者从海洋资源、海洋生态环境、海洋产业、海洋文化和海洋制度等方面构建评价指标体系并加以分析,其中海洋资源和海洋生态环境属于基础性因素,海洋产业和海洋文化等属于提升性因素[3-4]。
目前我国海洋产业体系逐渐成熟,但也出现产业发展同质化、科技支撑能力弱和科研成果转化难等问题,阻碍海洋经济的高效发展[5]。为实现青岛海洋经济的高质量发展,助力海洋强国目标的实现,本研究从海洋产业结构转型升级的角度出发,选取相关评价指标,采用Lasso回归模型分析对青岛海洋经济发展产生重要影响的海洋产业,并提出发展建议。
1 研究方法
当多个解释变量对被解释变量进行预测时,通常采用最小二乘估计法进行线性回归,但该方法对于基础回归存在一定的局限性。①出于最小化均方误差的目的而追求较低的偏差,导致方差变大,使得模型的泛化能力较差;②在线性回归中通常保留大量的解释变量,导致模型的可解释性降低。本研究应用具有较强影响力的解释变量子集,因此选择Lasso回归模型,从而克服普通最小二乘估计法的上述不足[6]。一方面,Lasso回归模型通过对线性回归系数施加约束和惩罚,将某些噪音变量的系数估计值压缩至0,从而将其剔除并筛选出重点变量;另一方面,由于变量个数的减少,Lasso回归模型往往表现出很强的泛化能力,预测效果通常优于线性回归。
通过求解目标函数的最小值得到Lasso回归模型的系数,目标函数的表达式为:

式中:n表示数据样本量;p表示数据特征个数;yi表示第i个被解释变量的样本值;xij表示第i个解释变量的第j个样本值(i=1,2,…,10;j=1,2,…,p);βj表示p维特征矩阵的待估系数;λ表示调节系数;RSS表示残差平方和。
除线性回归要求RSS达到最小外,Lasso回归模型增加回归系数的惩罚项:
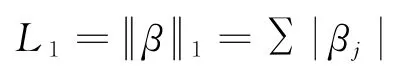
式中:L1表示回 归系数β=(β1,β2,…,βp)的惩罚项[7]。
λ控制对回归系数的惩罚力度。随着λ的逐渐增大,系数估计值逐渐减小。当λ足够大时,为使目标函数达到最小值,L1能够将某些变量的系数估计值强制设定为0,从而将这些不重要的变量从模型中剔除。因此,Lasso回归模型能够通过λ的取值来确定留在模型中的变量个数,进而得到稀疏模型,使模型更易于解释。
通常采用坐标下降法求解Lasso回归系数,该方法可在每步迭代中沿某个特征(坐标)的方向进行搜索,通过循环使用不同特征以达到目标函数的局部最小值。具体算法包括3个步骤:
(1)对j维向量β随机取初值,记为,上标括号里的数字代表当前迭代的轮数,此时为初始轮数0。
(2)对于第k轮迭代,从第一个维度β1(k)开始,到第j个维度βj(k)为止。每次迭代仅更新β的1个维度,即将该维度视为变量,将剩下的(n-1)个维度视为常量,通过最小化目标函数(求导或一维搜索)找到该维度对应的新值,得到
(3)检查向量βk和βk-1在各维度的变化情况。如果其在所有维度上的变化均足够小并小于设定的阈值,那么βk即最终结果;否则转入步骤2,继续第(k+1)轮迭代。
λ的取值直接影响变量筛选的最终结果,对于Lasso回归至关重要。在确定λ的最优取值时,可采用赤池信息准则(AIC)、贝叶斯信息准则(BIC)和交叉验证(CV)。其中,AIC和BIC同时考虑模型的拟合程度,并对模型中的变量系数进行惩罚;二者的不同之处在于,BIC将未知变量系数的惩罚权重由常数2变成样本容量的对数函数[8]。
交叉验证可分为留一交叉验证和K折交叉验证,其中留一交叉验证为K折交叉验证中的折数K等于样本量时的特殊情况。最常用的是10折交叉验证(K=10),具体操作方法为将所有样本平均分为10份即10折,以其中的9折作为训练集进行模型训练,以剩余的1折作为测试集(或称验证集)计算训练模型预测的均方误差。以此类推,10折中的每一折轮流作为训练集和测试集,计算10个均方误差的平均值,即最终的交叉验证误差。不同的λ会得到不同的交叉验证误差,当交叉验证误差最小时即得到λ的最优取值,并用其建立最终的模型。
与信息准则相比,交叉验证的计算量较少且操作方便,因此本研究采用经典的10折交叉验证进行λ的取值。
2 评价指标
2.1 指标选择
本研究参考和总结已有研究成果,综合青岛海洋经济发展现状,充分考虑评价指标及其数据的全面性、可获取性和代表性,选取海洋渔业、海洋化工业、海洋进出口总额、海洋环境、海洋交通运输业和滨海旅游业6个大类并细分20个特征变量,构建青岛海洋经济发展水平评价指标体系(表1)[9-10]。
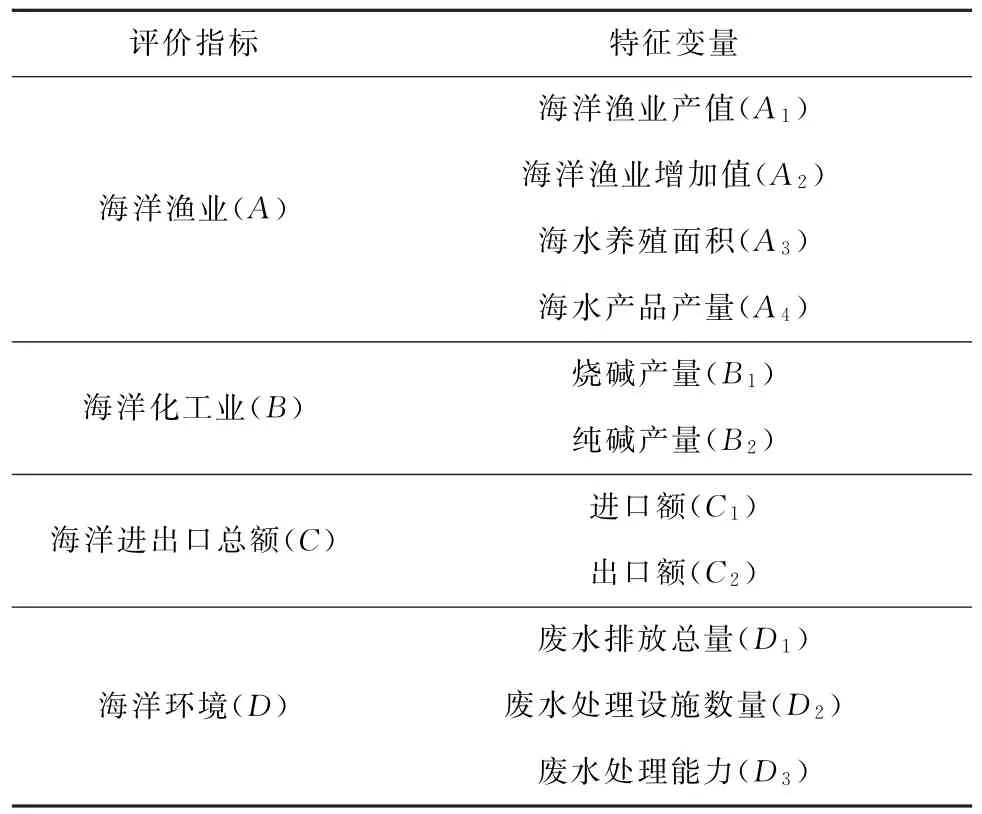
评价指标 特征变量海洋渔业(A)海洋渔业产值(A 1)海洋渔业增加值(A 2)海水养殖面积(A 3)海水产品产量(A 4)海洋化工业(B)烧碱产量(B 1)纯碱产量(B 2)海洋进出口总额(C)进口额(C 1)出口额(C 2)海洋环境(D)废水排放总量(D 1)废水处理设施数量(D 2)废水处理能力(D 3)

评价指标 特征变量海洋交通运输业(E)货运量(E 1)客运量(E 2)货物吞吐量(E 3)旅客周转量(E 4)货物周转量(E 5)滨海旅游业(F)入境旅客数量(F 1)入境旅游收入额(F 2)国内旅客数量(F 3)国内旅游收入额(F 4)
其中,海洋渔业增加值是指海洋渔业及其服务业通过生产产品或提供服务而增加的价值;废水处理能力是指平均每日的废水处理总量;旅客周转量是指旅客数量与运送距离的乘积;货物周转量是指货物量与运送距离的乘积。
2.2 数据处理
为分析特征变量对青岛海洋经济发展水平的影响程度,本研究选取2010—2019年青岛海洋经济发展水平评价指标的变量数据作为建模样本,不仅满足数据的时效性要求,而且在一定程度上降低模型的信息冗余。选取的实证分析数据主要来自历年《青岛统计年鉴》中关于海洋产业的公开数据,程序实现采用SPSS和R等软件[11]。
本研究对原始数据的预处理包括2个方面。①采用时间序列趋势预测的方法插补缺失数据。由于部分年份的数据记录问题,海洋化工业大类下的烧碱和纯碱产量存在不同程度的数据缺失。为充分利用现有数据并最大限度地提高模型回归结果的准确性,本研究利用1949—2013年的烧碱产量和1965—2015年的纯碱产量对其进行趋势预测,从而完成对缺失数据的插补。②采用数据标准化的方法消除指标量纲的影响。由于评价指标反映产业种类、发展潜力和优势特点等各方面的海洋经济发展水平,各评价指标下的特征变量量纲存在巨大差异。例如:海洋渔业产值以人民币计量,而海洋进出口总额则以美元计量,存在汇率的差异,此外数量和长度等指标也不具有可比性。为消除指标量纲的影响,本研究对原始数据进行标准化处理。
3 实证分析
3.1 特征变量的描述性统计和相关性
各评价指标特征变量的描述性统计如表2所示。

特征变量 平均值 标准差 最小值 最大值A 1 169.73 23.33 118.19 193.69 A 2 4 803.97 5 198.92 0.83 11 608.91 A 3 3.46 0.28 3.15 4.01 A 4 108.68 3.97 100.79 113.41 B 1 18.79 11.12 9.78 35.36 B 2 67.22 2.93 61.70 72.07 C 1 2 414.04 2 250.31 567.21 5 779.56 C 2 3 022.53 2 940.20 598.83 6 944.38 D 1 5.03 0.75 4.04 6.34 D 2 430.20 48.74 346.00 486.00 D 3 100.84 56.84 37.48 172.10 E 1 2 310.10 1 131.70 1 313.00 4 407.00 E 2 423.90 357.70 161.00 1 302.00 E 3 4.72 0.72 3.50 5.77 E 4 70.99 91.22 0.30 196.73 E 5 1 541.81 987.47 427.00 3 237.40 F 1 135.01 18.17 108.05 170.26 F 2 61.76 20.35 39.97 108.40 F 3 1 185.82 432.12 540.00 1 897.20 F 4 7 273.55 2 159.16 4 396.00 11 132.58
由于特征变量的个数较多,变量之间易出现信息重复、相关或冗余的现象,从而导致多重共线性等问题。基于此,本研究计算特征变量的斯皮尔逊线性相关系数,并对其进行相关性分析。经计算和分析,海洋经济发展水平的特征变量之间存在强相关性,其中海洋渔业产值与海水养殖面积、客运量和货物吞吐量之间的相关系数均超过0.90,进口额与出口额和旅客周转量之间的相关系数甚至超过0.99,表明海洋经济发展水平评价指标体系中的某些变量存在冗余信息,应予以剔除。因此,本研究剔除特征变量中的重复变量,筛选重要变量并构建Lasso回归模型。
3.2 模型构建
3.2.1λ的最优取值
在Lasso回归模型中,λ直接决定进入模型的变量个数,进而影响模型回归的准确性。随着λ的不断增大,本研究中20个特征变量的系数依次缩减到0,即相应变量可从模型中剔除。其中,系数最晚缩减到0的特征变量对被解释变量预测的重要性最强,以此类推。
为使Lasso回归模型的结果更加准确,采用10折交叉验证确定λ的最优取值。本研究中每个特征变量的可用样本量仅有10个(2010—2019年),即每折仅有1个样本,因此10折交叉验证等价于留一交叉验证,即每次留1个样本作为测试集,其他9个样本作为训练集,进而得到训练模型在测试集中的均方误差。最后,取10个测试集均方误差的平均值作为交叉验证误差,以最小交叉验证误差对应的λ为最优取值。
10折交叉验证误差随λ取值变化的曲线如图1所示。其中,上下闭口的竖直线表示交叉验证误差的95%置信区间,第一条虚线表示当交叉验证误差最小时对应的λ和模型自由度(变量个数),第二条虚线表示交叉验证误差增速由低到高的转折点。
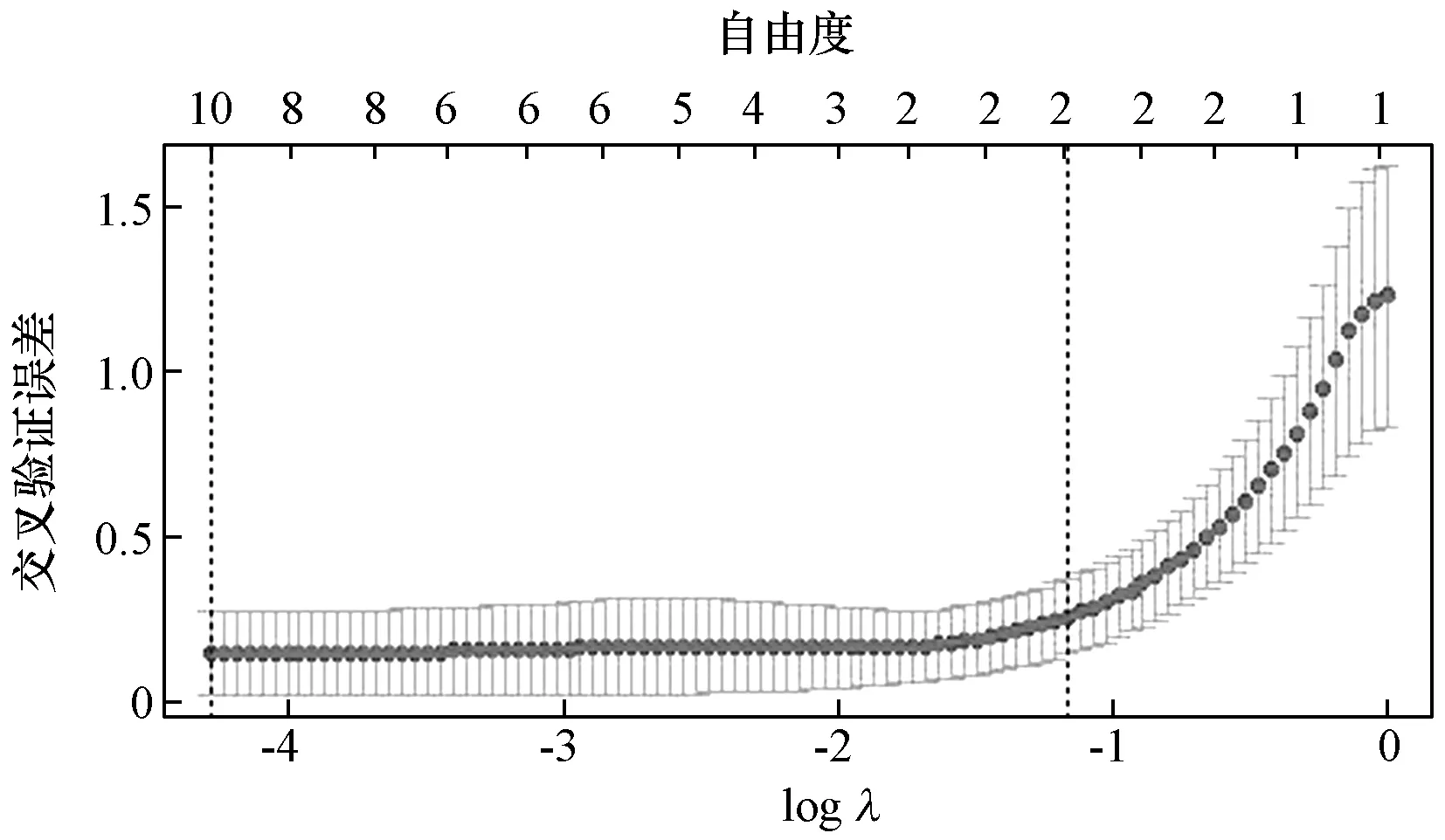
图1 交叉验证误差和λ的取值
由图1可以看出:随着logλ的增大,Lasso回归模型的交叉验证误差缓慢增大;当logλ增至-1附近时,交叉验证误差增速骤升;当λ=0.013 76即logλ=-4.286 0时,交叉验证误差达到最小值即0.001 0。因此,λ的最优取值为0.013 76,此时模型中含有10个特征变量。
数值形式的模型自由度、交叉验证误差和λ如表3所示。
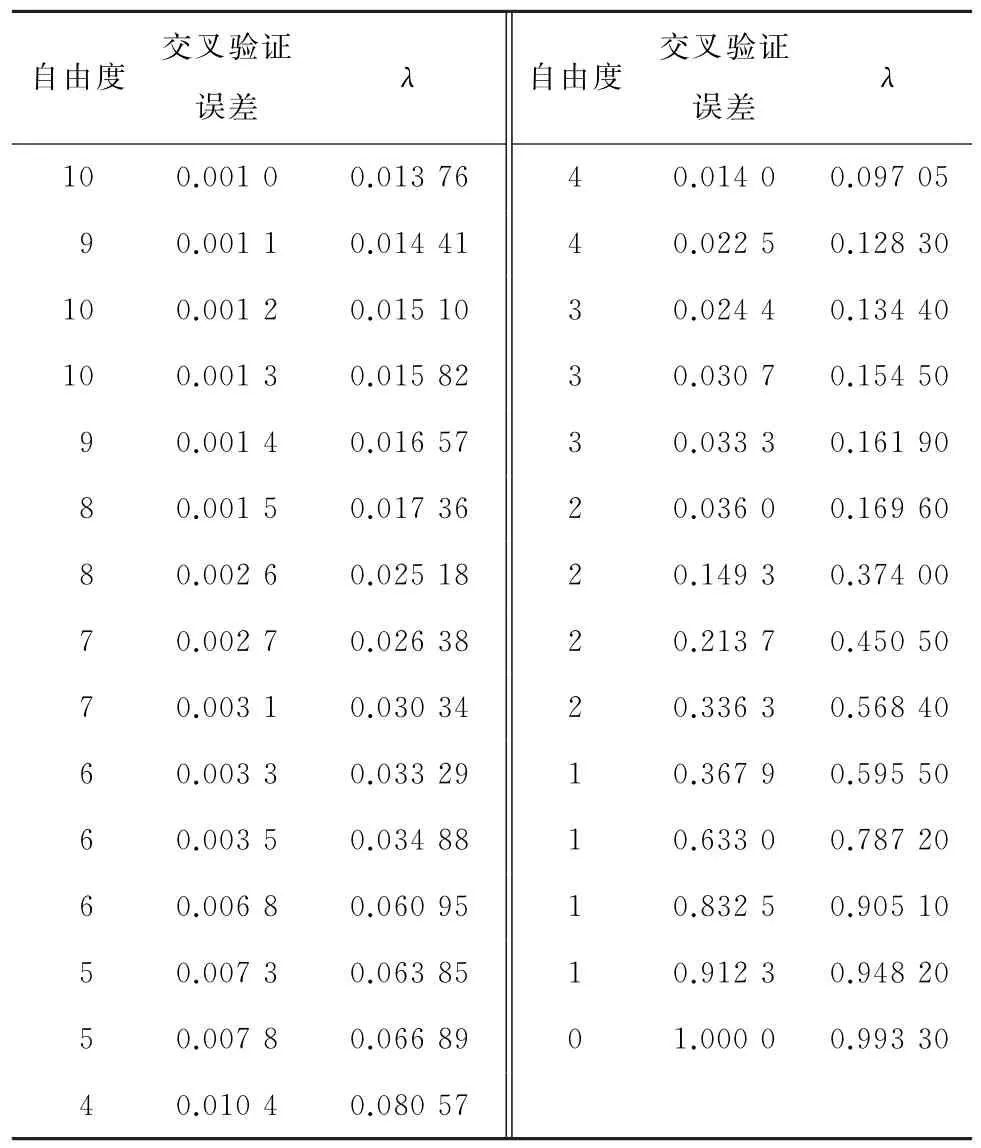
自由度交叉验证误差 λ 自由度交叉验证误差 λ 10 0.001 0 0.013 76 4 0.014 0 0.097 05 9 0.001 1 0.014 41 4 0.022 5 0.128 30 10 0.001 2 0.015 10 3 0.024 4 0.134 40 10 0.001 3 0.015 82 3 0.030 7 0.154 50 9 0.001 4 0.016 57 3 0.033 3 0.161 90 8 0.001 5 0.017 36 2 0.036 0 0.169 60 8 0.002 6 0.025 18 2 0.149 3 0.374 00 7 0.002 7 0.026 38 2 0.213 7 0.450 50 7 0.003 1 0.030 34 2 0.336 3 0.568 40 6 0.003 3 0.033 29 1 0.367 9 0.595 50 6 0.003 5 0.034 88 1 0.633 0 0.787 20 6 0.006 8 0.060 95 1 0.832 5 0.905 10 5 0.007 3 0.063 85 1 0.912 3 0.948 20 5 0.007 8 0.066 89 0 1.000 0 0.993 30 4 0.010 4 0.080 57
根据λ由小变大和由大变小2个维度进行分析。①当λ由小变大时,自由度不断减小,当λ=0.993 30时的自由度为0,此时模型中不再含有变量,且交叉验证误差达到最大值即1.000 0;②当λ由大变小时,交叉验证误差整体不断减小,且当λ=0.013 76时,交叉验证误差达到最小值即0.001 0,由此得到λ的最优取值即0.013 76,此时模型中含有10个变量,这与图1的验证结果相对应。值得注意的是,当λ由0.015 10减至0.014 41时,交叉验证误差由0.001 2减至0.001 1,自由度由10减为9;随着λ的继续减小,交叉验证误差随之减至0.001 0,但自由度又增至10。这种现象表明λ的取值依赖于交叉验证误差,既考虑模型的拟合程度,又考虑模型中的变量个数。
基于上述分析,本研究采用λ=0.013 76建立Lasso回归模型,并采用坐标下降法求解Lasso回归系数。
3.2.2 Lasso回归系数
对20个原始特征变量的待估系数β=(β1,β2,…,β20)随机取初值,采用R软件进行正态模拟,生成正态随机数并记为β0(表4)。

序号 正态随机数 序号 正态随机数1 0.918 977 11 1.358 680 2 0.782 136 12 -0.102 790 3 0.074 565 13 0.387 672 4-1.989 350 14 -0.053 810 5 0.619 826 15 -1.377 060 6-0.056 130 16 -0.414 990 7-0.155 800 17 -0.394 290 8-1.470 750 18 -0.059 310 9-0.478 150 19 1.100 025 10 0.417 942 20 0.763 176
对于第一轮迭代,从第一个特征变量即海洋渔业产值对应的系数β1(1)开始,到第二十个特征变量即国内旅游收入额对应的系数β20(1)为止。每次迭代仅更新1个特征变量对应的待估系数,即将该系数视为变量,将剩余的19个系数视为常量,通过目标函数对该系数求偏导的方式得到其对应的极小值,如此可得Lasso回归系数迭代1次的解,记作;然后继续迭代,此时出现当部分系数取值为0时目标函数才能取得极小值的情况,可将这些系数对应的变量从模型中剔除;持续迭代直至目标函数取值的变化足够小,可将此时的系数作为最终结果。
由于系数估计值较复杂且数量较多,本研究不再展示求解过程。结果表明有10个特征变量的系数估计值为0,在求解过程中将其从模型中剔除。最终的Lasso回归模型中共含有10个特征变量,其系数估计值和进入模型的顺序如表5所示。

评价指标 特征变量 系数估计值 进入模型的顺序海洋渔业海洋渔业产值 0.129 368 0 3海洋渔业增加值 0.008 927 0 8海水养殖面积 -0.164 600 0 2海洋化工业烧碱产量 0.034 346 0 7纯碱产量 0.004 349 0 9海洋进出口总额 出口额 0.049 385 0 6海洋环境废水排放总量 0.046 163 0 5废水处理能力 -0.056 210 0 4海洋交通运输业 货物吞吐量 0.000 060 2 10滨海旅游业 国内旅客数量 0.556 582 0 1
3.3 回归结果
采用10折交叉验证确定λ的最优取值为0.013 76,图1和表3分别以曲线和数值的形式将确定λ最优取值的过程具体化。λ的取值取决于交叉验证误差,既考虑模型的拟合程度,又对模型中的变量个数加罚,能够显著提高模型的泛化能力。由于原始数据已进行标准化处理,整体变化幅度较小,模型中的变量系数也较小,但仍可根据系数估计值判别各变量的重要性。
由表5可以看出,Lasso回归模型筛选变量的重要性存在差别。其中,国内旅客数量的系数估计值最大即重要性最强,而货物吞吐量的重要性较弱;海洋渔业产值的系数估计值明显大于绝大多数变量,表明其对青岛海洋经济发展具有显著影响,海洋渔业在所有海洋产业中表现较为突出也是青岛海洋经济发展的明显特征之一;在滨海旅游业中,国内旅客数量因系数估计值最大而被最先选入最终模型,成为关键性变量,且其在整个评价指标体系中的地位也十分显著;海洋化工业中的烧碱产量和纯碱产量均被保留,但烧碱产量的重要性明显高于纯碱产量;海洋交通运输业中仅有货物吞吐量被保留,但其系数估计值最小,表明其对青岛海洋经济发展的贡献较小,尚存在广阔的发展前景。
在模型回归效果方面,应用Lasso回归模型对10个关键性变量的原始数据进行拟合,并将拟合值与真实值进行对比,得到整体平均预测误差为0.000 98,表明预测准确率较高,且模型泛化能力和可信度远高于普通最小二乘估计法的线性回归。在相同条件下,若采用多元线性回归,由于变量个数远大于样本量,得到的设计矩阵为非列满秩矩阵;尽管此时的平均预测误差接近于0,但这样的回归结果很可能是不可靠的,甚至无法得到准确的系数估计值。因此,本研究接受Lasso回归模型的预测结果,并得到稳健的稀疏模型。
4 发展建议
4.1 进一步发挥滨海旅游业和海洋渔业等产业的优势
滨海旅游业是青岛的支柱产业,应充分挖掘海洋文化和丰富旅游项目,给各地旅客带来新鲜感和体验感,尤其应完善相关基础设施建设,为旅客提供“一站式”服务,提高旅客黏性;严格实行禁渔制度,定期放苗,保护海洋生态环境,促进海洋渔业的可持续发展[12]。
4.2 着力发展海洋交通运输业,提高青岛港口的影响力
货轮拥有装载量大和运输成本低等特点,适合发展国际贸易。青岛应抓住“后疫情时代”的发展机遇,提高青岛港口的装卸效率,通过智能化的码头和空轨集疏运系统,由平面交通向立体交通升级;积极“走出去”,与世界名企联合,建设世界一流的国际化港口。
4.3 保护海洋生态环境,提高废水处理能力
近年来我国大力倡导绿色发展,在发展经济的同时保护环境已是社会各界共识。青岛是依托海洋发展的城市,海水养殖业、海洋交通运输业和滨海旅游业等主要产业的可持续发展都对海水质量有很高的要求。因此,亟须完善“废水入海”的管理制度和标准,加大执法力度和科研投入,着力提高对工业和生活废水的处理能力,使海洋生态文明建设更上新台阶。
4.4 加大海洋科技研发投入,提高成果转化能力
海洋经济的跨越式发展须依靠海洋科技的促进和支撑。应制定科学的海洋经济发展规划,优化海洋产业结构,大力培养海洋人才,以科技促发展,实现海洋经济发展方式的转型升级[13]。

