基于神经网络密集匹配的资源三号DSM提取

韩昊，李参海，丘晓枫

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.自然资源部国土卫星遥感应用中心，北京 100048)

0 引言

立体匹配是一种从不同视角影像中寻找像点对应关系的技术，通过立体匹配对多视航空航天遥感图像进行三维场景重建一直是摄影测量与遥感中的核心问题[1]。随着我国资源三号系列立体卫星的陆续成功发射组网[2]，卫星的立体匹配及数字地表模型生成成为了研究热点。几十年来，立体匹配作为一个经典的研究主题，传统上被描述为一个多阶段优化问题，包括匹配代价计算、代价聚合、视差优化和后处理。匹配成本计算是立体匹配的第一步，它为左图像块和可能的相应右图像块提供了初始相似性度量。传统的立体匹配方法利用像素周围图像块的低级特征来测量差异。通常使用一些常见的局部描述符，例如绝对差(absolute difference，AD)、CENSUS、BRIEF、归一化互相关(normalized cross-correlation，NCC)或它们的组合(例如AD-CENSUS)[3]。

已有的立体匹配算法可以分为局部匹配算法、全局匹配算法、半全局匹配算法以及基于深度学习的立体匹配[4]。局部方法运行速度非常快，但是质量通常较差。全局匹配算法匹配效果较局部方法效果更好，但由于全局匹配算法本身的计算复杂度高、时间长，因此很难应用到大像幅的遥感影像匹配。Hirschmüller[5]提出的半全局匹配算法在匹配效果和计算效率方面有较好的平衡，而且比较容易实现并行加速，因此被广泛应用于近景、航空影像匹配中[6]，取得了很好的效果。立体卫星影像具有较大几何和辐射差异，在使用半全局立体匹配(sim-global matching，SGM)算法匹配时通常会出现误匹配和视差空洞。

近些年以神经网络为首的机器学习算法在多个领域取得了突破性进展，计算机视觉与深度学习的结合给遥感带来了新的研究热点。在近景影像立体匹配方面，基于深度学习的立体匹配算法已经胜过Kitti和Middlebury立体数据集上的每个SGM派生算法。通常将基于深度学习的立体匹配方法分为三类[7]：非端到端学习算法、端到端学习算法以及无监督学习算法。对于非端到端立体声方法，引入了卷积神经网络(convolutional neural network，CNN)来替换传统立体匹配算法中的一个或多个流程。Zbontar等[8]首先成功地将匹配代价替换为深度学习的方法，并且在准确性和速度方面都比传统方法获得了更可观的效果。Shaked等[9]设计了一种新的高速网络架构，用于计算每种可能差异下的匹配成本。Seki等[10]提出了一种SGM-Net来计算SGM的代价。通过精心设计和监督神经网络，还可以通过端到端的深度学习方法获得精细的视差，无需进行后处理。随着Mayer等[11]的成功，端到端立体匹配网络在立体匹配算法中变得越来越流行，端到端的网络通常网络层数多、训练时间长、计算时间较慢，不适合数据量较大的卫星遥感影像。在过去的几年中，基于空间变换和视图合成，已经提出了几种用于立体匹配的无监督学习方法。Garg等[12]使用从泰勒展开中得到的不完全可区分的图像重建损失训练神经网络进行深度估计。但迄今为止，无监督的深度解决方案虽然产生了令人鼓舞的初步结果，但是目前在实际使用中仍不能获得可靠的信息。

目前深度学习的立体匹配方法已经被标准测试集成功验证，并广泛应用于车载立体匹配[13]以及无人机避障[14]，在遥感影像的立体影像处理尚不成熟。刘瑾等[15]研究了深度学习的方法在航空遥感影像密集匹配上的性能。本文将基于孪生网络的立体匹配方案用于国产线阵卫星影像，并与基于半全局匹配(sim-global block matching，SGBM)生成数字地表模型(digital surface model，DSM)的算法效果进行对比，证明了本文算法提取效果较好，提取结果能够达到与商业软件相近。

1 基于孪生网络密集匹配的DSM提取流程

提取流程共分为三大部分：预处理部分、密集匹配部分以及数字地表模型提取部分。

1.1 影像预处理

预处理分别应用于每个经正射纠正后的立体对，共分为四个步骤，如图1所示。其目的是产生两个主要输出：①立体校正网格，该网格可将一对图像重新采样为完美对齐的几何形状；②视差范围的估计值。

步骤1：此步骤包括根据传感器模型RPC(rational polynomial coefficients)和初始低分辨率数字地表模型(例如SRTM)估算立体校正网格。这些网格用于对立体对中的图块逐块重采样，本文使用一种基于核线约束的几何形状的近似迭代[16]，这种方法递归地估计两个纠正网格。这些网格可与连接点一起将输入图像重新排列为核线影像。

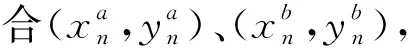
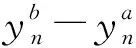
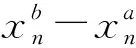
1.2 孪生网络密集匹配生成视差图

在进行影像预处理后，计算左右影像视差图。通过立体匹配计算视差图，然后使用传感器模型对视差进行空三计算以获得3D点。将匹配所得的目标地形区域(默认为成对覆盖的最大区域面积)依据视差图划分为地形图块，并形成遮挡掩码，重叠地形图块仅计算一次。

密集匹配的流程可分为代价计算、代价聚合、视差计算、视差精化4个步骤。本文算法将孪生神经网络MC-CNN(matching-cost CNN)计算匹配代价引入资源三号密集匹配生成数字地表模型流程中。MC-CNN包括两种结构的网络：Fast和Slow结构，前者的网络结构处理速度更快，但所生成视差值精度稍逊于后者。由于Slow网络对训练数据量和计算机内存均有较高要求，本文采用Fast网络作为实验网络。网络框架如图2所示。

1)代价计算。这里引入孪生网络模型用来学习相似性度量(similarity measure)，即进行代价计算。输入为左右一组图块，输出是它们之间的相似性。两侧卷积层用于分别提取左右图块高维特征，两侧网络模型共享权值。模型结构末尾设置了一个特征提取器及归一化层，目的是将图像块表示成特征向量的形式，然后对这两个特征向量进行比较。决策网络以点积作为相似性度量，对提取的共有特征计算点积并输出结果。根据点积的大小反映左右两样本之间的相似性。

网络的训练通过输入相同图像位置为中心的样本对来计算损失，其中一个样本属于正类别，一个样本属于负类别。通过使铰链损失函数最小化，进行网络训练。铰链损失函数定义为：max(0，m+s--s+)。s-为负样本的输出；s+为正样本的输出；余量m为正实数。也就是说，正样本要比负样本至少大m，loss的值才为0。通过最小化铰链损失来训练网络，实验中将m设置为0.2。

网络最终输出的匹配代价由M来表示，代价M的计算方法如式(1)所示。

(1)

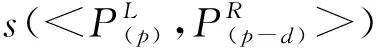
2)代价聚合。在计算匹配代价后需进行代价聚合，采用可变十字交叉代价聚合(cross-based cost aggregation，CBCA)[18]方式。CBCA 的目标是找到像素p周围颜色相似的像素，并按照一定的规则将它们的代价值聚合成像素p的最终代价值，聚合窗口如图3所示。图3中像素p的支持区域是合并其垂直臂上的所有像素的水平臂，pl为左侧水平聚合臂，q是p的垂直臂上的某个像素，p的聚合区域就是所有q(包括p自身)的水平臂的并集。

3)视差计算及精化。视差图D通过赢家通吃策略(winner takes all，WTA)进行计算，即寻找使M(p，d)最小的视差d(式(2))。

D(p1→2(xe，ye))=argmindM(p，d)

(2)

式中：D(p1→2(xe，ye))为视差图；p为像点；d为视差值。MC-CNN在视差优化方法上采用了与SGM相同的策略，匹配后经过亚像素增强、中值滤波以及双边滤波进行处理。本文采用窗口为5×5的中值滤波器。

1.3 生成数字地表模型

1)视差图转换为3D点云。从视差图p1→2，使用g1和g2获得传感器像空间中的同源点集H，计算如式(3)所示。

H(x，y)=(g1(xe，ye)，g2(xe+d1→2(xe，ye)，ye))

(3)

根据这些点，使用前方交会计算出对应视线，并将这些线与3D点位置相交。出于数值精度的考虑，此计算先在ECEF坐标中完成，后转换为WGS84坐标[19]。通过将此交点应用于所有视差图中已计算的视差，形成一个3D点云P=(x，y，h)k。

2)栅格化。最终的数字地表模型是通过点云的栅格化生成的，即将上文计算的3D点云转换为地理定位的栅格图像。对于地形网格的每个像元，根据所定义的分辨率形成像元中心，对于像元中心(cx，cy)，寻找一组与其欧氏距离小于k·res的点C，计算如式(4)、式(5)所示。

dc(x，y)=‖(x，y)-(cx，cy)‖

(4)

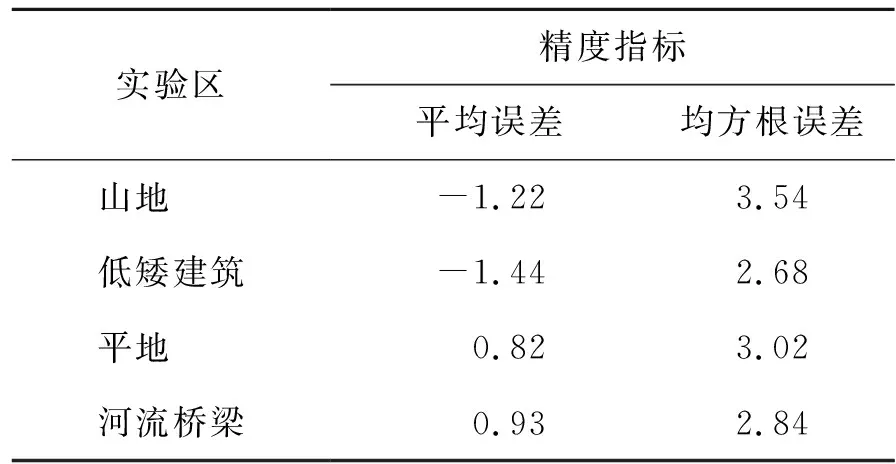
C=(x，y，h)∈P，dc(x，y)

(5)

式中：dc为视差；C为点集；res代表分辨率；k为用户设定的参数；h为中心点的高程值，通过在一定范围内对3D点进行高斯加权来获得。高斯加权方法如式(6)所示，并最终生成数字地表模型栅格图。

(6)

式中：h为高程值；C为点集；e为常数;σ为标准差。

2 实验分析

2.1 孪生网络模型及参数设置

本文模型训练采用了佐治亚理工学院[20]提供的5×5窗口孪生神经网络预训练模型，并在预训练模型基础上进行精细化二次训练，以节约训练时间。分支网络超参数如表1所示。

表1 分支网络超参数

2.2 训练数据与平台

在采用预训练模型进行迁移学习的基础上，添加80%WHU MVS(wuhan university multi view stereo)航空影像立体数据集[21]与20%Middlebury立体数据集进行模型精细化训练，共选取325组影像对。采用混合数据集是为了增加模型的泛化能力。本文从325训练图像对中提取了12 800个示例，一半标为正类，一半标为负类，并将图像转化为灰度图像。通过减去平均值并除以像素灰度值的标准偏差来预处理每张图像。训练时网络每批的输入是128对图像块，在预测时，网络两端输入一对核线立体像对输出相似性分数。

1) WHU MVS数据集。WHU MVS航拍影像数据集涵盖了贵州省梅丹县约6.7 km×2.2 km的地区，距离地面 550 m 处拍摄地面分辨率为0.1 m，大小为 5 376像素×5 376像素的1 776张图像，并有相对应的 1 776 个深度图作为地面实况，且提供了总共1 760张沿飞行方向的视差图。该数据集中涵盖了六个代表性的子区域，这些区域涵盖了不同的立体匹配场景类型，分别为工厂与郊区、树木与道路区、居民区、复杂屋顶区、城镇中心区、农业用地和山区，可直接作为深度学习方法的训练和测试集。

2) Middlebury数据集。Middlebury 立体数据集中的影像对是由Middlebury学院拍摄的多组室内场景。受控的照明条件使得其比 KITTI 数据集和Driving数据集具有更高的密度和视差精度。Middlebury 数据集中的图像显示了具有不同复杂度的静态室内场景，包括重复结构、遮挡、线状物体以及无纹理区域。Middlebury2003、2005、2006与2014 数据集共包含 65 个高分辨率立体影像对，并使用结构光扫描仪获得的相机校准参数和真实视差图。

3) 训练平台。本文孪生网络的训练和测试在Ubuntu系统下NVIDIA Tesla K80显卡上进行，采用Jupyter Notebook IDE、PyTorch1.5框架，精细化训练共迭代50次。由于本文在预训练模型基础上精细化训练，学习速率设置为0.000 3。

2.3 数字地表模型提取实验

资源三号01、02、03星分别于2012、2016、2020年发射升空，填补了中国立体卫星领域的空白。本文选取02星于2019年拍摄的河北邯郸地区一组质量较好的前后视影像进行实验，影像分辨率2.5 m，实验区影像如图4、图5所示。实验区分为复杂山区和多地形影像两组，多地形影像包含了山地、建筑物、河流、桥梁、平地等多种地貌。

数字地表模型生成及评价实验均在Ubuntu系统下，Intel Core i7-660U 2.60 GHz CPU上进行，使用Python编程语言进行程序编写。

2.4 实验结果分析

1) DSM定性结果分析。首先对所生成视差图进行定性分析，分别对影像中的典型复杂山地区域、丘陵区域、建筑物区域、平坦地区生成的未经填充且未添加DEM辅助[22]的5 m分辨率数字地表模型效果进行对比。从图6、图7、图8中可以看出，本文方法通过卷积操作深度提取了匹配块的特征，相较SGBM方法在实验区的山区能够通过密集匹配生成连续视差，具有更好的DSM提取效果，山体部分匹配效果更加理想，SGBM算法在高分辨率数字地表模型提取时存在大量的误匹配和视差空洞。但两种方法均未在连续阴影及视差较大的区域取得良好效果。本文在低矮建筑物、桥梁匹配相较SGBM算法细节也更为突出，在平原地区的低矮建筑物DSM提取边缘更加清晰，密集建筑物误匹配现象更少。

2)DSM精度分析。在精度分析方面，针对每种地表类型选取适量可靠检查点，将本文方法生成的DSM中无视差空洞部分与PCI Geomatica 2018软件生成的5 m分辨率DSM进行精度对比。PCI Geomatica是世界级的专业地理信息服务商PCI公司的旗舰产品，是目前最优秀的卫星数字地表模型生产软件之一，其生成的DSM精度与效果通常优于MicMac、ASP等同类软件[23]。PCI生成的DSM如图9所示。图9中可明显看出，在视差空洞部分，即图中圆圈圈出部分，软件对所生成的DSM进行了填充或模糊处理，且PCI的DSM生成添加了低分辨率DEM作为辅助填充。精度对比由平均误差、均方根误差两个指标对比完成，结果如表2所示。

表2 DSM精度对比 m

从表2中数据可看出，本文方法生成的5 m分辨率DSM在各种地物类别中的误差均值接近于0，均方根误差较小，其中山地误差较大，这主要是由于山地通常匹配难度高、视差大、遮挡较多。平均误差数值在0±1.5 m内，证明与PCI所生成DSM差别很小，验证了本文方法生成DSM的可靠性。

3 结束语

本文提出了一种基于孪生神经网络的资源三号卫星影像立体匹配方法，通过孪生神经网络密集匹配实现了国产资源三号系列02星影像的立体匹配，并实现了高精度、高分辨率的DSM提取。运用孪生网络提取匹配块的深度特征，并计算匹配测度，提高了资源三号影像的密集匹配效果。在具有复杂地貌的立体影像上进行实验，与传统方法做了比较，验证了本文方法在卫星遥感影像立体匹配生成DSM方面效果与商业软件效果相近，且匹配效果优于基于半全局匹配的方法。本文的研究为开展1∶2.5万以及更大比例尺DSM的生产提供了新的技术思路。