基于差异图融合和FLICM聚类的SAR图像变化检测

董宝兰，汪骏，毕津滔

(1.黄山学院 信息工程学院，安徽 黄山 245000；2.衢州学院 机械工程学院，浙江 衢州 324000)

0 引言

合成孔径雷达(synthetic aperture radar，SAR)采用的是主动式的遥感成像模式[1]，具备全天时与全天候的成像特征，已经成为了遥感领域技术研究的热点方向。SAR图像变化检测是对同一地区的多时段的SAR图像做比对，获取该地区变化信息的描述图谱，以实现对该地区地物变化的综合分析，其结果已广泛应用于植被生长监测、灾情评估、资源探测、城镇发展研究等众多应用领域[2-3]。然而SAR图像往往存有相干斑噪声，致使其图像处理和变化检测更为困难[4-5]。

SAR图像变化检测从整体流程上看，主要分成下面几个步骤：SAR图像预处理、差异图生成、差异图分析与后处理[6]。SAR图像预处理操作主要有图像配准和几何校正、滤波操作、辐射校正等。差异图构建的方法常用的有差值算法、比值算法、对数比值(log-ratio，LR)算法、均值比(mean-ratio，MR)算法、组合差异图(combined difference image，CDI)算法、邻域比值(neighborhood-based ratio，NR)算法等。其中，差值法是将两个时刻SAR影像同一位置上的像素点的强度值直接相减，该算法虽简单易行，然而对乘性随机噪声敏感，且从误差校正的角度来讲，并不具备稳定性与鲁棒性[7]。比值法是计算两个时刻SAR影像的强度比值，并以此来衡量其变化与否[8]。比值算子虽然能够比较好地抑制相干斑噪声，但是未能进一步考虑影像的类条件分布、边缘信息和局部信息等先验知识。LR算法是在比值算法的前提下增加一步对数的计算[9]，将SAR影像更换到对数尺度上来，进而将乘性噪声变换成加性噪声，加强了变化类和未变化类间的对比度。然而，LR算法的非线性收缩能力导致其检测结果模糊了边缘区域的像素值。MR算法是利用了像素点所在邻域的均值信息，以其替代中心像素点的强度值来度量差异。MR算法一定程度上降低了噪声对像素强度的影响，使得变化检测的结果更加平滑，但是对成片形式出现的噪声，其抑制效果有限[10]。CDI法是由Zheng等[11]所提出的一种差异图融合方法，该算法分别对差值差异图、对数比值差异图做均值滤波、中值滤波处理，之后运用人工加权设置的参数对其做线性组合，以取得融合差异图。该算法虽然处理速度较快且简单易行，但需要人工设置参数，不能根据图像自身的特性进行自动选择。NR算法是由Gong等[12]提出的基于邻域信息比值的差异图生成算法，与MR算法的区别在于NR算法是运用异质性测度值作为权重比，对比值差异图和MR差异图做加权平均，该权值可以对异质区域和匀质区域进行有效区分，提高了变化检测方法的鲁棒性。差异图的分析方法常用的有基于阈值、基于水平集、基于聚类、基于图割等多种差异图分析算法。阈值法主要是通过对差异图建立模型，根据其统计分布的特点找出最优阈值，然后将该阈值作为边界划分差异图为变化类、非变化类[13]。水平集法本质上是把曲线演化的问题转换成曲面演化，采用隐含方式来求解分割曲线，并使用迭代方式来求水平集函数值为零的解所构成的曲线集合，从而获取图像分割结果[14]。聚类法是运用预设的目标函数将差异图进行类别的聚集，使得同一类内的距离最小，同时各类别之间的距离最大[15]。图割法的实质就是把变化类、未变化类的标签逐一分配给各像素点，根据预定的约束函数来指导类别的分配，当标签分配结果所对应的能量值达到最小时，图像的各像素点就是对应于最优化的标签[16]。

本文针对传统差异图生成方法的不足，提出了一种基于融合差异图的SAR图像变化检测算法。首先，以对数比和滤波比法产生两幅不同表征的差异图；然后，设计融合算子α作为权重，综合两幅差异图的特征信息，获得新的高可分性的融合差异图；最后，采用局部信息模糊C均值聚类(fuzzy local information c-means，FLICM)算法进行分类，分离出其中的变化区域和未变化区域。实验选用漏检数、误检数、正确率、Kappa系数作为评价指标[17]，对算法做定性和定量的对比分析。分析结果说明，本文的算法增强了抗噪性能，变化检测的准确率与精度也有了显著的提高，且适用范围更广。

1 本文算法

定义I1和I2是已经配准和校正过的同一地区在不同时间获取的两幅SAR图像，大小均为M×N。基于差异图融合和FLICM聚类的SAR图像变化检测算法的具体处理流程如下。

步骤1：对I1和I2分别构造对数比值图和滤波比值图，获取Dg、Ds两幅初始差异图。

步骤2：采用新的融合算子α作为权重，将对数比图和滤波比值图进行组合，得到新的差异图DI。

步骤3：基于FLICM聚类算法对DI进行分类，获取最终的变化检测结果。

具体算法流程如图1所示。

1.1 融合差异图生成

对数比值图和滤波比值图的计算如式(1)、式(2)所示。

(1)

(2)

首先，在求对数比值图Dg的过程中为了避免 Ii的值为0，导致式(1)无意义，使用 Ii+1(i=1，2)代替Ii(i=1，2)。然后，通过归一化，使其灰度值分布范围为[0，255]。其次，在求滤波比值图Ds的过程中，先将两幅图像做SRAD滤波[18]处理，从而使得获取的图像δ1、δ2更加平滑，再进行比值计算。

LR算子经常应用于差异图的构建，它将SAR图像的乘性噪声变换成相对更易处理的加性噪声，并且压缩了比值图像的变化范围，增加了变化类、非变化类二者之间的对比度，但是模糊了边缘区域的像素值，不能保留变化区域的真实信息。滤波比算子使用滤波平滑后的图像比值代替原来像素的值，考虑了像素的空间邻域信息，具有保留图像边缘细节同时减少噪声的作用，但是易模糊背景。因此，使用单一类型SAR差异图的生成信息会导致检测精度低且适用性不高。基于上述问题，本文提出融合算子α作为权重，运用加权平均的方式对两幅初始差异图进行融合，如式(3)所示，这样不仅凸显了变化区域，还抑制了噪声影响。

DI=αDg+(1-α)Ds

(3)

融合算子α的计算如式(4)所示。

(4)

式中：μ1(x)、μ2(x)分别表示采用SRAD滤波平滑处理后的SAR图像δ1和δ2的以x为中心的邻域块(大小为r×r) 的强度均值；ν1(x)、ν2(x)分别表示采用SRAD滤波平滑处理后的SAR图像δ1和δ2的以x为中心的邻域块(大小为r×r)的灰度变化。此外，关于融合算子归一化的问题，式(4)中α的理想值为[0，1]，但是当ν1(x)+ν2(x)>μ1(x)+μ2(x)时，该值可能会大于1，进而导致组合差异图DI取值为负，从而无法精确地表示变化关系，因此采用式(5)对α值做归一化处理。

(5)

1.2 基于FLICM的差异图分析

传统的模糊C均值聚类方法[19]对噪声敏感，未考虑到被分割图像的空间邻域信息，往往得到的分割效果不太理想。因此，Krinidis等[20]在此基础上引入了模糊因子，提出了FLICM聚类算法。该算法是在图像分割中结合空间信息和灰度信息，保留了图像的细节，减少了噪声对图像分割的干扰，加强了鲁棒性。FLICM聚类算法采用迭代计算模糊因子、聚类中心、隶属度矩阵，实现了给定聚类数下的图像分割。

2 实验结果及分析

本文分别选取了两组不同地区的真实SAR图像进行变化检测，以验证本文所提算法的可行性、适用性、有效性。通过对同一数据集的实验仿真，将本文算法与均值法、对数均值比法、邻域比值法所构造的差异图做比较，之后运用FLICM算法做差异图分析对比实验。

2.1 实验设置

第一组SAR图像数据是由Radarsat SAR卫星所拍摄的渥太华地区受洪水影响的同一区域前后两时相的SAR图像，分别如图2(a)、图2(b)所示。采集时间分别是1997年5月和8月，图像大小都是290像素×350像素，灰度为256。图2(c)为地物变化参考图。

第二组SAR图像数据是由Gaofen-3 SAR卫星所拍摄的淮河地区受土地覆盖影响的同一区域前后两时相的SAR图像，分别如图3(a)、图3(b)所示。采集时间分别为2017年6月和9月，图像大小都是554像素×780像素，灰度为256。图3(c)为地物变化参考图。

2.2 变化检测精度评价

为了对所获取的SAR图像变化检测结果做后续客观的定量或者是定性的评价，通常将得到的变化检测结果和真实的变化参考图做对比，以分析其地物结构的变化，因此设立了4种指标内容，如表1所示。可以通过表1变化误差矩阵中的指标进一步计算得出正确分类精度(precision of correct classification，PCC)和Kappa系数，从而对变化检测的结果进行定量评定。

表1 变化检测误差矩阵

2.3 实验结果与分析

图4为渥太华地区4种对比算法构建的差异图，图5是经过FLICM聚类后的变化检测结果图。图4(a)和图4(b)的差异图有明显的变化信息，但噪声也相对较多，在图5(a)和图5(b)的检测结果中也存在较多的杂点；图4(c)的邻域比值差异图变化信息不太明显且存有较多噪声，在图5(c)的检测结果中也有较多漏检和误检；而本文算法利用了对数比值图和滤波比值图的融合(图4(d))，变化信息相对更为明显，既能有效降低噪声的影响，又能将图像细节保留得更为完整。

渥太华地区的变化检测精度结果如表2所示。从表2数据可以看出，本文算法的检测性能优于其他3种方法，且误检数与漏检数之和最低，检测正确率提高到98.49%，总体变化检测精度Kappa系数也提升到0.942 8。

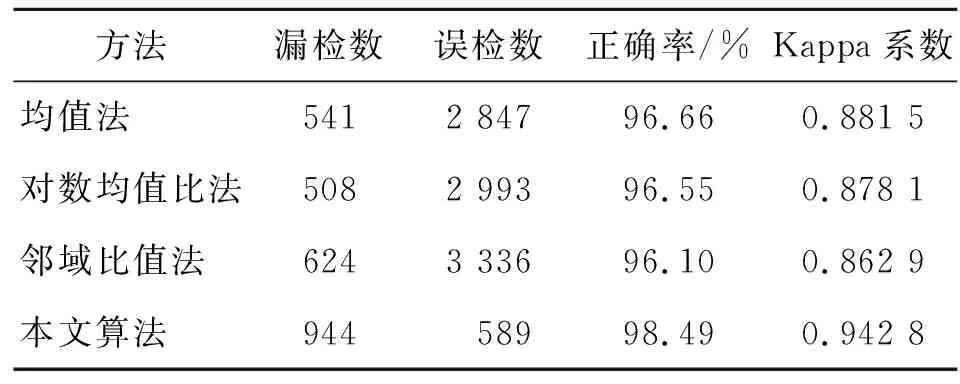
表2 渥太华地区变化检测结果性能分析

图6为淮河地区数据4种对比算法构建的差异图，图7是经过FLICM聚类后的变化检测结果图。图6和图7可以直观地显示出，这4种对比算法能有效检测出该地区大部分的变化信息，但相比而言，本文算法更接近参考变化图，可以在抑制噪声干扰的同时保护好图像的边缘细节。图6(a)的均值比差异图虽然变化特征信息明显，但噪声也相对较多，在图7(a)的检测结果中也存在较多杂点；图6(b)的对数均值比差异图噪声减少，但是抑制了变化特征信息的强度，导致了图7(b)中漏检数较多；图6(c)的差异图变化信息较不明显，且存在较多噪声点，因此图7(c)中漏检和误检情况都比较严重。

淮河地区数据变化检测精度如表3所示。从定量分析数据表可以看出，本文算法的总体错误数最少(即漏检数、误检数之和最低)，将检测正确率提高至97.81%，总体变化检测精度Kappa系数也提高了2.03%～7.42%。从实验数据可以看出，本文算法显然优于其他3种算法，能够更加有效地提取地物变化信息，并且提高了抗噪性能。

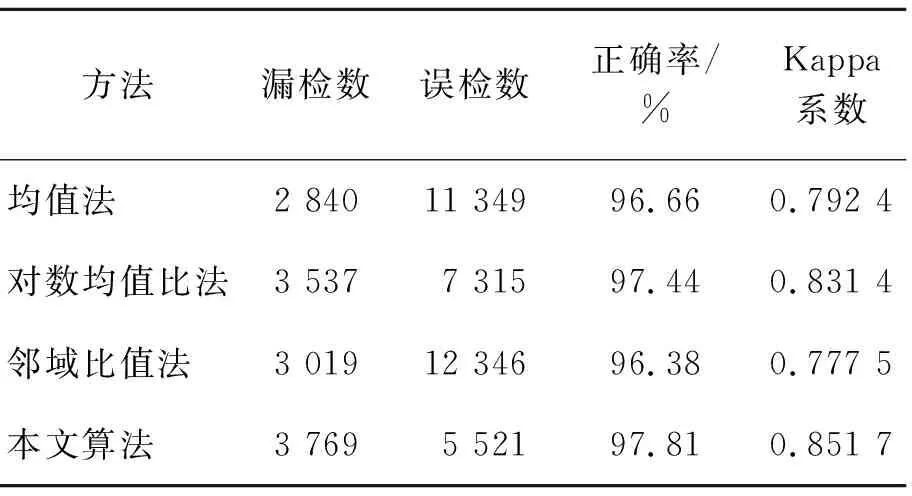
表3 淮河地区变化检测结果性能分析

3 结束语

本文综合考虑传统差异图生成方法的优缺点，提出了一种基于差异图融合和FLICM聚类的SAR图像变化检测算法。该算法采用对数比法和滤波比法生成两幅不同表征的差异图像，设计融合算子α作为权重，综合两幅差异图的特征信息，获取新的高可分性的融合差异图，之后运用FLICM聚类算法对融合差异图做分类，获得最终的变化检测结果。实验结果表明，本文提出的方法可以有效地提高变化检测的准确率和精度，在保持图像细节的同时具有更好的相干斑噪声抑制能力，适用范围较广。该算法的应用有效减少了误检数，但是会增大漏检数且损失一些边缘信息，因此如何平衡二者并提高SAR图像的变化检测精度，将是今后进一步研究的重点。