问题驱动：一把实现高效课堂的密钥——“用导数证明不等式”教学实录与反思

◎吕金晶 （浙江省嵊州中学，浙江 嵊州 312400）

前 言

浙江省教育厅“百人千场”名师送教暨嵊州中学课堂教学展示同课异构活动于2022年3月4日在浙江嵊州隆重举行.本次活动以人教版数学选择性必修第二册第五章“导数在研究函数中的应用——用导数证明不等式”为同课异构教学内容.笔者有幸参加了此次活动，并与各位名师一起上了这堂同课异构课.现将本堂课的教学实录与反思一一呈现，以期批评指正.

1 教材解析

导数是微积分的核心内容之一，是现代数学的基本概念，蕴含着微积分的基本思想；导数定量地刻画了函数的局部变化，是研究函数增减性、变化快慢、最大（小）值等性质的基本方法，因而也是解决诸如增长率、膨胀率、效率、密度、速度、加速度等实际问题的基本工具.本节课是一节综合应用课，目的是让学生在掌握用导数研究函数的单调性、极值和最值后，用导数的相关知识证明不等式.

2 教学目标

2.1 通过具体函数的图像，发现函数间的不等关系，体会数形结合思想，发展直观想象素养.

2.2 观察不等式（）≥（）（或（）≤（））的结构，能构造辅助函数（），把不等式证明问题转化为利用导数研究函数（）的单调性和最值等问题.

2.3 结合信息技术手段进行图像演示，让学生亲历感知和发现的过程，培养学生推理演绎的能力，发展逻辑推理核心素养.

3 教学重点与难点

重点：掌握利用导数证明不等式的基本方法——构造函数法.

难点：在证明过程中出现的隐零点问题及函数的二分法.

4 教学实录

引导语：通过对本章的学习，我们知道，导数是研究函数的法宝，它定量刻画了函数的局部变化，是研究函数单调性、变化快慢、最大（小）值等性质的基本方法.今天，我们接着来学习：用导数证明不等式.

4.1 教材实例 引入新课

图1

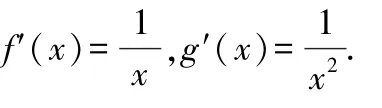
①当0＜＜1时，（）＞（）＞1，说明（）的图像比（）的图像要“陡峭”；

②当＞1时，0＜（）＜（）＜1，说明（）的图像比（）的图像要“平缓”.

可知，代表（）的图像、代表（）的图像.

学生通过观察思考分析出函数所对应的图像，既是对前面所学知识的应用，也可为后续问题的提出做好铺垫，起到承上启下的作用.

请同学们继续观察这两个函数的图像，是否存在相应的不等关系呢

在学生自主发现后，教师引出本节课的主题，让学生直观感知函数间的不等关系，充分调动学生的主观能动性，加强学生对不等关系进行抽象概括的能力，并为后面不等关系的证明做好铺垫.

4.2 探索新知 深化课堂

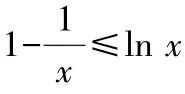
学生思考并回答，学生到黑板上板演.

教师再次梳理证明过程，证明（）≥（）⇔（）-（）≥0，通过作差法构造（）＝（）-（），利用导数研究（）的单调性和最值，从而证得（）-（）≥0.

对于类似不等式的证明，是否只能通过作差法来构造函数

学生1：可以用作商法构造函数.

学生2：还可以用换元法构造函数.

学生3：还可以用对数法构造函数.

教师：非常好！根据不等式本身的结构特点，我们可以构造一个新的函数，通过研究该函数的性质证明不等式.

通过一道典型不等式的证明题，一方面温故知新，夯实基础，另一方面通过师生互动总结出构造函数法是证明不等式的基本方法，落实本堂课的教学目标.

接下来我们回到原来的图像，两个函数图像都经过同一点（1，0），函数＝ln在点（1，0）处的切线的方程是什么同学们是否能发现其中的不等关系如图2所示）

图2

学生4：切线方程为＝-1，且由图可知，直线＝-1的图像恒在＝ln图像的上方，可知，ln≤-1.

追问1：你会如何证明这个不等式呢？

学生4：通过构造函数法不难证得.

教师：回答得非常好！我们可以通过对这个重要不等式ln≤-1进行适当换元，从而得到形形色色的不等式，这也正是对数不等式的“万花筒”特性.

通过比较函数图像，培养学生的直观想象能力，初步培养学生对超越函数进行切线放缩的意识，同时巩固用导数证明不等式的方法.

4.3 推波助澜 升华课堂

我们再次回到对数函数＝ln上，它的反函数为指数函数＝e，可知它们的图像关于直线＝对称，请同学们观察它们有怎样的不等关系.

学生观察，集体回答，有e＞ln，＞0.

如果加大难度，将函数＝e的图像向右平移两个单位长度，得到＝e的图像＝e与＝ln又有怎样的不等关系呢

学生6：从图像的角度，不难看出e＞ln，但是如何严谨地证明它，我还要再想想.

请同学们来谈谈，要证明这个不等式：e＞ln我们有哪些方法

学生7：可以通过作差法构造函数.

学生8：可以通过切线放缩，由e≥-1，ln≤-1，不难得到e＞ln

教师：都非常有想法！

从同一个对数函数＝ln入手，引入它的反函数＝e，再从学生的原有知识基础入手，让学生亲历动态的变化过程，将学生的思维引向深处，引发其基于问题的思考，为后续的动手演练打下伏笔.

基于刚才的思考，同学们是否可以写出严格的证明过程请动手操作.

全班同学动笔证明，教师请一位学生上台板演证明过程.

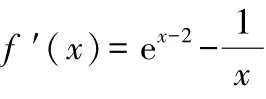
教师：请先回到自己的座位.同学们，让我们一起来找找问题出在哪里了.

追问1：为什么会出现这个情况呢？

学生9：隐零点的范围（1，2）找得太大了.

追问2：有什么办法可以改进范围？

教师：请同学们在学生7的基础上改进他的证法.

教师：回答得非常棒！

让学生用构造函数法这一基本方法来证明这个不等式，牵引出隐零点的相关知识，让学生体会隐零点灵活多变的用法，同时渗透二分法来改进问题.本环节通过不断追问将问题层层递进，推向高潮，也实现了知识间的融会贯通.

同学们是否可以从切线放缩的角度给出严谨的证明呢

全班学生动笔证明，教师请一位学生上台板演证明过程.

学生8：设（）＝e-+1，＞0，那么（）＝e-1，当∈（0，2）时，（）＜0，即（）在（0，2）上单调递减；当∈（2，+∞）时，（）＞0，即（）在（2，+∞）上单调递增，则（）≥（2）＝0，当且仅当＝2时，等号成立，从而e≥-1.

要证明（）≥（），可以观察不等式的结构特征，通过构造函数法来证明；也可以通过寻找一个简单的过渡函数（），通过证明不等式组（）≥（）≥（），从而证得（）≥（）.尤其是当两个超越函数同时出现时，更需要对不等式进行转化，来降低做题的难度，这一方法实则是切线放缩的思想.

4.4 大道至简 小结课堂

一个主题：用导数证明不等式.

两种方法：构造函数法和放缩法.

一类思想：数形结合思想.

4.5 回归本质 检测课堂

（1）求，；

（2）证明：（）＞1.

3.已知函数（）＝e-ln-1.

（1）设＝2是（）的极值点，求，并求（）的单调区间；

5 教学反思

利用问题驱动数学教学，是指教师需要深入挖掘知识背后的深刻问题，结合学生实际，创设真实高效的问题情境，将问题融入情境让学生在探究活动中自然生成概念、性质、法则等，并获得相应的思想与方法.

5.1 立足学生的问题设计

问题是数学的心脏，立足于学生主体的问题设计，更能起到画龙点睛的作用.我们知道，学生是课堂的主体，问题的设置和推进应贴近学生的客观实际.在宝贵的课堂时间内，教师立足于学生主体的恰到好处的提问既是提高课堂效率、增强学生注意力的有效方法之一，也是激发学生思维、加速问题解决的催化剂.因此，教师在备课时要根据学生的实际情况来设计问题串，并因材施教，这样才能实现课堂效能最大化.

5.2 立足学生的教学设计

5.2.1 遵循课堂限定的教学目标

教学目标是课堂教学活动的根本，只有制定合理的教学目标，才能有序开展教学活动.教师应以课堂教学目标为指导，根据学生已有的知识基础，精心设计问题串，通过阶梯式的提问，循循善诱，让学生在思考中解决问题，在解决问题中实现教学目标的顺利达成.

5.2.2 采撷课堂中的闪光点

数学课堂应该是灵动的.在课堂教学中，处处都会碰撞出思维的火花，时时都可能有学生的奇思妙想，这或许是与原本的问题设计不一致的.此时，教师应敏锐地捕捉学生思维的闪光点，将它变为打开学生思维枷锁的钥匙.

6 结束语

《麦肯锡教我的思考武器：从逻辑思考到真正解决问题》一书中写道：“用有力的思考去解决工作当中的真正的问题.”我们倡导以问题驱动学生的学习，其实质就是让问题为学习提供源动力，引发学生真思考、真探索、真研究，从而促使学生深度学习的发生，让学生的核心素养得以生成.问题驱动让学习“基于问题、为了问题、在问题中”.通过这堂课，笔者认识到：问题驱动教学法对教师提出了更高要求，教师必须具备较强的课堂掌控能力，课前，教师既要了解学科的知识特点，也要关注学生现有的认知水平，提出针对性的问题；课堂上，教师要关注学生自主学习、合作探究、讨论交流等活动；课后，教师要予以恰当评价，着眼长远，关注能力，重视品格，聚焦素养.如此，问题驱动教学法才能真正成为推动高效课堂生成的有力抓手.