基于多媒体算力驱动视域下数据智能物流非线性控制
冉鸿雁
(四川化工职业技术学院 四川省泸州市 646300)
随着多媒体算力驱动生态系统是指一个物理的或抽象的实体,具备感知周遭环境,并正确调用自身所有知识对环境做出适当反应的能力。依据此概念,自然界中的多数生物体,如候鸟、昆虫等,和现代社会中的大多智能装备,如数据智能无人机最后一公里配送、数据智能数据智能物流车辆配送及各类交叉研究的机器人等,均可视为多媒体算力驱动生态系统。作为多媒体算力驱动视域下数据智能物流的一个重要应用领域,数据智能物流网络化控制与容错控制系统可实现多车间感知、决策和控制的协同作用。而数字能智能化与智能物流汽车技术的多媒体算力驱动视域下数据智能物流被认为是智能交通系统的主要实现形式,对破解道路拥堵、数据智能物流车辆事故等城镇化难题具有重要研究意义。
1 系统问题描述
考虑如下具有双积分器运动特性的多媒体算力驱动生态系统描述为:

其中,q和p分别为第i 个多媒体算力驱动生态系统的位置向量和速度向量,u为施加在多媒体算力驱动生态系统i 上的感知输入,n 为多媒体算力驱动生态系统的个数。假设所有多媒体算力驱动生态系统的感知和通信范围均为R,则多媒体算力驱动生态系统 的相对集可定义为:


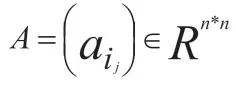




2 多媒体算力驱动生态模型
2.1 多媒体算力驱动生态运动学模型
假设多车系统中每辆车均为四轮独立驱动前轮转向结构,则在侧偏角较小时,数据智能物流车辆的多媒体算力驱动生态运动学模型可简写为:

其中,X,Y分别为第i 辆车在全局坐标系下的纵向和横向位移,θ为数据智能物流车辆的航向角,v为数据智能物流车辆的速度,在小侧偏角下近似等于数据智能物流车辆的纵向车速,ω为数据智能物流车辆的横摆角速度。
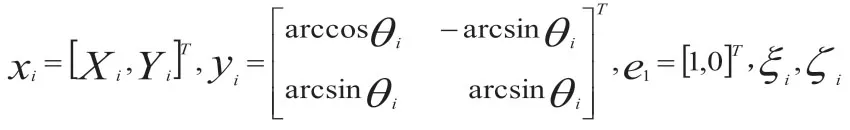

式(6)可转变为:

式中:

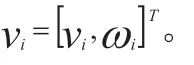

2.2 多媒体算力驱动生态运动模型
在仅涉及数据智能物流车辆平面运动下,数据智能物流车辆的3 自由度多媒体算力驱动生态运动模型可写为:
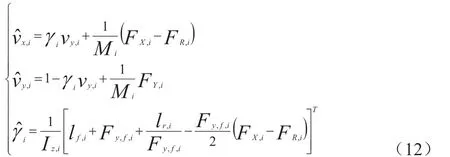
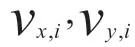
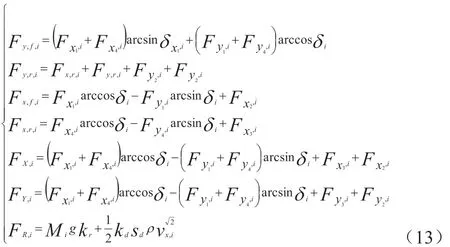
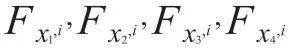

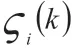

则数据智能物流车辆非线性系统(15)可为:
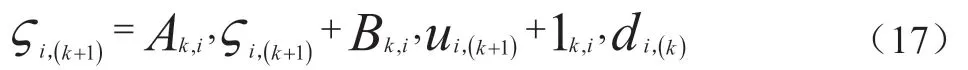
式中

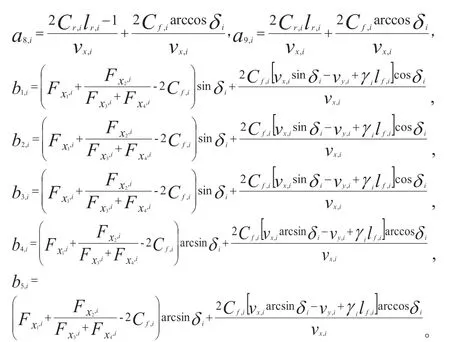
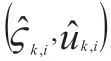
3 数据智能物流驾驶队列成形分分布式控制模型
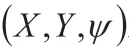
3.1 数据智能物流驾驶分布式控制器设计
3.1.1 数据智能物流车辆动力学稳定边界
由于本文仅考虑数据智能物流车辆的平面运动,在此基础上其稳定性边界主要由纵向车速和横摆角速度约束条件构成。根据式(12),数据智能物流车辆的侧向加速度可重新表示为:


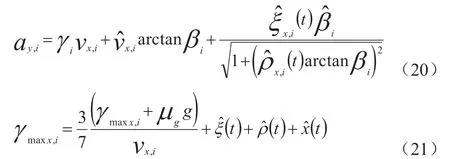
在此基础上,数据智能物流车辆横摆角速度应该满足:
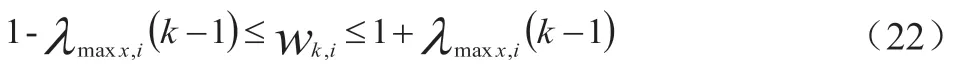
在此基础上,为了保证足够的数据智能物流车辆轮胎力,每个数据智能物流车辆车轮的载荷都必须大于零。同时,数据智能物流车辆纵向加速度应满足:

式中:h为数据智能物流车辆质心的高度。除了以上因素外,在实际数据智能物流车辆行驶过程中,为了防止出现数据智能物流车辆侧滑,数据智能物流车辆的纵向力F和侧向力F不应超过地面所能承受的最大摩擦力,在此基础上有:

结合式(23)和(24)可得:

其中,
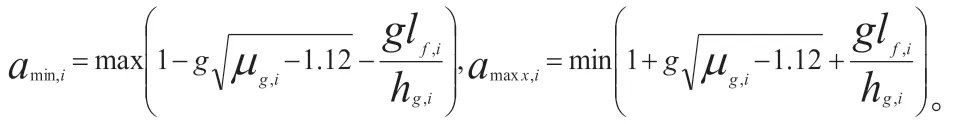
根据式(25),可得到:


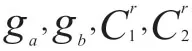
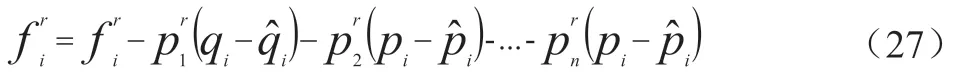
综合以上分析,则优化变量矩阵可选择为:
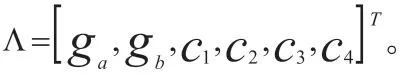

式中:Q,p为权重,N为正常数,v为数据智能物流车辆的最大车速,表示为:
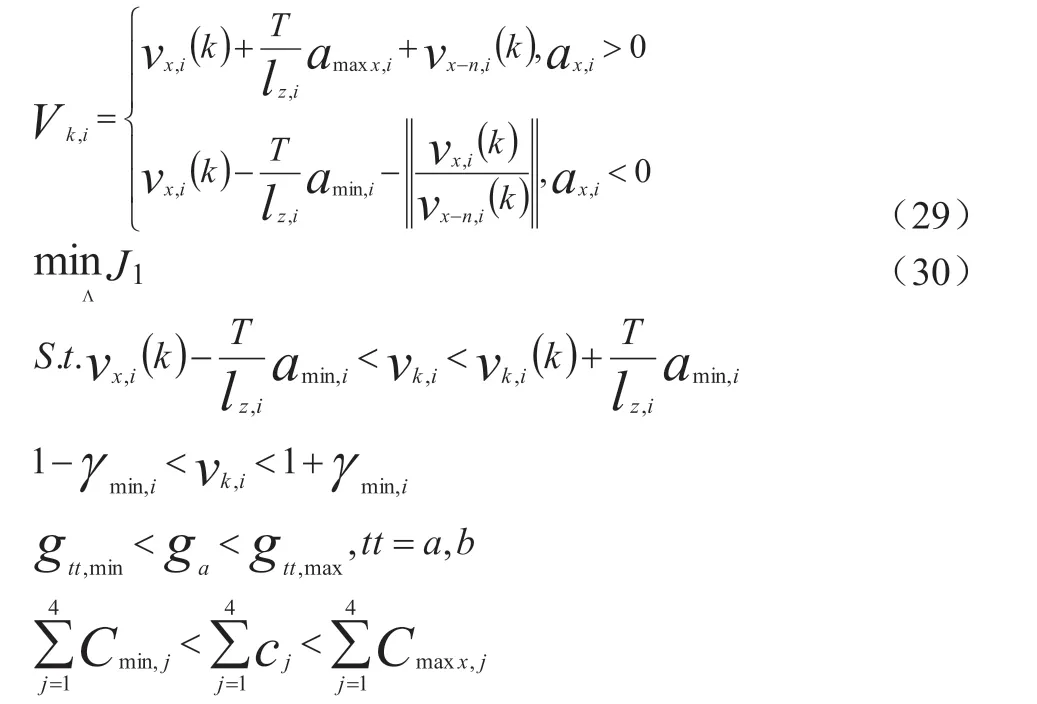
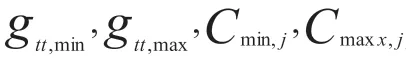
3.2 数据智能物流驾驶跟踪层控制器设计
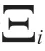

根据规划控制器所生成的参考状态,在 时刻的有限预测时域内最优控制问题的代价函数可写为:
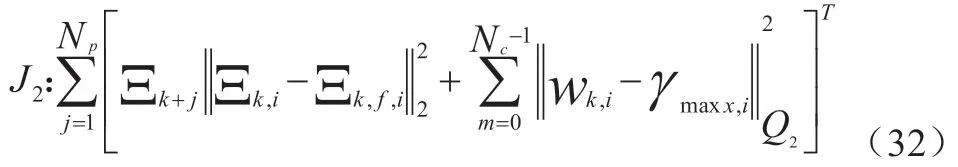




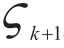
(1)研究了多车队列控制问题中数据智能物流车辆侧向动力学和执行器饱和问题。基于数据智能物流车辆稳定边界,并结合多媒体算力驱动生态系统群集控制算法,设计了一种稳定高效的分布式多媒体算力驱动生态系统。
(2)提出了一种分布式路径跟踪控制器,形成了一种分层结构的控制体系,实现了数据智能物流车辆队列编队的稳定规划和跟踪。
(3)为了评估所提出的多媒体算力驱动生态系统的有效性,对具备不同速度、位于不同车道的五辆车进行了仿真。仿真结果表明,与传统的基于多媒体算力驱动生态系统群集算法的多车队列形成感知相比,所提出的控制器可以实现安全、高效的多车队列形成。

