基于集成学习方法对不均衡数据的处理

赵存秀

（山西科技学院 山西省晋城市 048000）

近年来，随着机器学习技术的不断发展，越来越多的科研人员将机器学习应用于安全评估、疾病诊断及临床研究中的类别预测模型的研究。关于分类算法及其应用已经有很多的研究，但基于类别不平衡的数据（两类别个数差别很大），仍然是预测模型发展的主要挑战之一。不平衡数据集的分类出现在许多实际的生物医学应用中。目前大多数分类算法的评价指标是正确预测的总数最大化。这一标准是建立在每一类误分类造成的损失相等的假设基础上的。当类别大小差异很大时，大多数标准分类器会倾向于更大的类。一般来说，多数类的预测精度较高，少数类的预测精度较低。但是实际研究中更多的是关注小类分类情况，传统的分类器就失效了。类别不平衡分类的一个主要挑战是开发一个能够为少数类预测提供良好准确性的分类器。

王荣杰等提出不平衡数据分类的矩阵粒加权集成分类算法。结果表明,矩阵粒加权集成分类算法具有较高的分类准确性,是对不平衡数据分类算法研究的一次有益尝试和补充。杨毅提出的B-SMOTE 是在SMOTE 的基础上把少数类的边界样本与少数类样本插值合成新训练样本，表明基于SMOTE 的集成学习算法能有效改善不平衡数据集的不平衡性。张宗堂等在提取的子训练样本集上分别训练基分类器,将其中少类间隔均值最大的基分类器作为本轮选定的分类器,迭代形成最终集成分类器。李勇等详细分析了不平衡数据集成分类算法的研究现状，集成学习是基于多个弱基分类器上做决策的机器学习技术,由于基分类器的弱相关性,因此提高机器学习效果。袁兴梅等鉴于最大间隔思想在很多分类问题中的优越性,将最大间隔思想引入到非平衡分类问题中,使用SVM 的方法取得了很好的分类性能。陈力等基于多次训练决策树进行仿真实验,发现使用AdaBoost 算法和GBDT 算法后准确率降幅较大,而改进的PFBoost 算法能够在保证准确率的情况下显著提升F1 值和G-mean 值,且在绝大多数数据集上的F1 值和G-mean 值提升幅度远超其它两种集成算法。基于不同的集成学习方法处理不平衡数据，研究哪种集成方法更适合于处理不平衡数据问题中。

1 算法介绍

集成学习方法是近几年非常流行的机器学习手段，通过将若干个弱学习器通过一定的策略集成一个学习能力较强的学习器。Bagging是一种直接的基于自助采样的典型学习方法。有放回的随机抽样训练集，每次试验的训练集有N个样本，将抽取的N 个样本用于一次训练，并对测试集进行预测。T 次循环后得到一个结果集。最终的预测结果对于分类问题对结果集采用投票的方式或者通过Stacking 学习。

1.1 投票

投票法就是在同一训练集上，训练得到多个分类或回归模型，然后通过一个投票器，输出得票率最高的结果，投票算法如图1。

图1 ：投票法算法流程

Bagged CART在使用Bagging 的每次训练中使用的是决策树（CART）用投票的方式得到最终的预测。随机森林（Random Forest）使用了CART 决策树作为弱学习器，在bagging 的基础上做了修正之后的算法：从总体中抽取的N 个样本，随机选择k 个特征，通过信息熵或者信息增益选择最佳分割特征作为决策树的左右子树划分，建立CART 决策树；重复以上两步m 次，即建立了m 棵CART 决策树；这m 个CART 树形成了随机森林，通过投票表决结果，决定数据属于哪一类别。

1.2 Stacking

Stacking具体集成框架如图2 所示。本次研究的弱分类器有Linear Discriminate Analysis (LDA) [线性分类器，类似的QDA]、Classification and Regression Trees (CART)、Support Vector Machine with a Radial Basis Kernel Function(SVM)三种。本次实验利用广义线性回归和random forest 两种学习方法进行第二次学习。

图2 ：stacking 集成

1.3 支持向量机

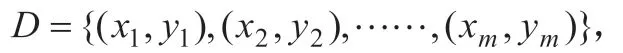
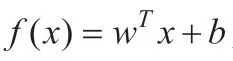
1.4 线性判别分析

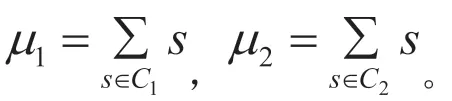
这样我们就可以将LDA 要解决的问题转化为带约束的优化问题：

1.5 CART剪枝算法

算法：(CART 剪枝算法)输入：CART 算法生成的决策树T0；输出：最优决策树Tα.(1)设k=0，T=T0.(2)设α=+∞.(3)自下而上地对各内部结点t 计算C(Tt)，|Tt|以及images/BZ_256_1355_912_1700_1083.png这里，Tt 表示以t 为根节点的子树，C(Tt)是对训练数据的预测误差，|Tt|的Tt 叶结点个数.(4)自下而上地访问内部结点 t，如果有 ，进行剪枝，并对叶结点t 以多数表决法决定其类，得到树T.(5)设k=k+1，images/BZ_256_1615_1326_1743_1375.pngTk=T.(6)如果T 不是由根节点单独构成的树，则回到（4）.(7)采用交叉验证法在子树序列T0,T1…Tn 中选取最优子树Tα

1.6 度量

针对二分类数据问题，通过实验将预测结果与数据真实情况类别进行比较，建立混淆矩阵，如表1。

表1 ：混淆矩阵

Kappa 值对于分类问题就是检验模型预测结果和实际分类结果是否一致。很多时候，直接用准确率来判断模型的好与坏，但重复实验，模型结果分布很不均匀时，准确率不一定是一个好的量度值。Kappa 的范围是[-1,1]，-1 表示完全不一致，0 为偶然一致，落于[0,0.2]表示极低的一致性(slight)，[0.21,0.4]一般的一致性(fair)，介于[0.41,0.6]为中等的一致性(moderate)，Kappa 值位于[0.61.0.8]为高度的一致性(substantial)，[0.81,1]几乎完全一致(almost perfect)。

2 验数据与训练模型

2.1 真实数据

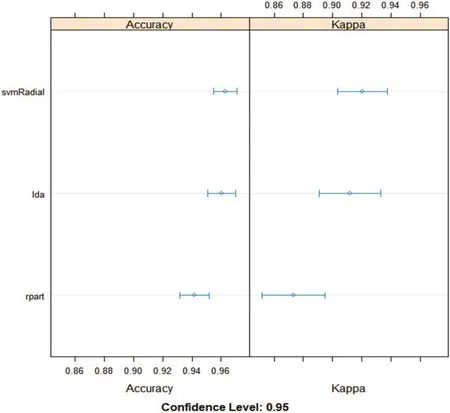
图3 ：3 个分类器的箱线图

本次实验采用的数据是美国威斯康星大学提供的人体乳腺肿瘤数据样本，将异常数据筛选，使得每个样本有11 个属性，截取部分数据如表2 所示，肿块厚度、细胞大小

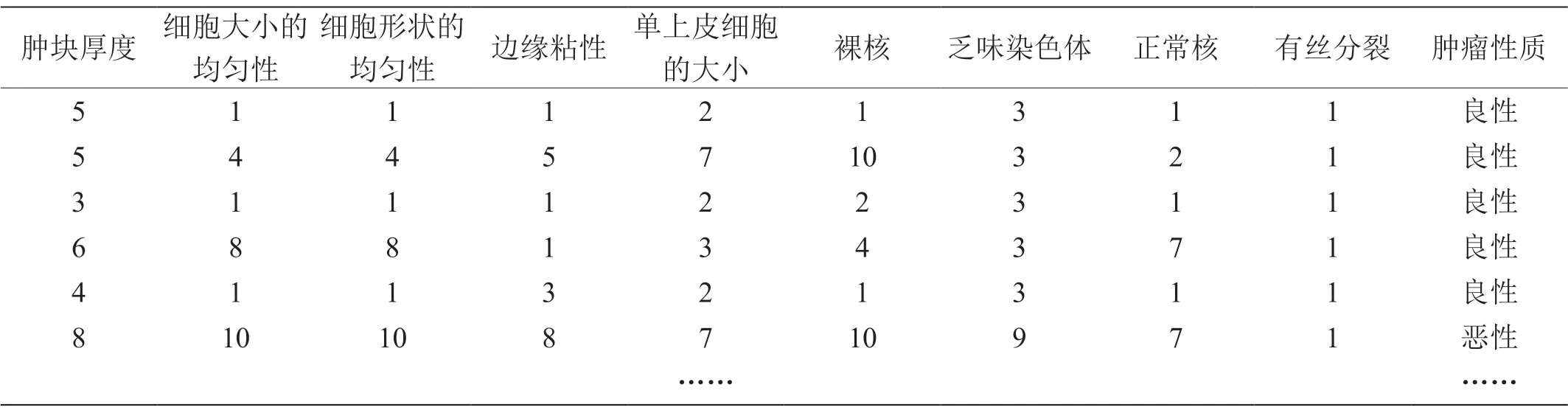
表2 ：乳腺肿瘤数据集

的均匀性等九项医学研究内容为样本的实际特征值，肿瘤性质为实验标签良性与恶性。样本总共有683 个实验数据，其中良性肿瘤有 444 个，恶性肿瘤有239 个。其中数据的70%为训练样本集，30%为测试样本集。

2.2 数据结果

两个较为典型的Bagging 算法：Bagged CART 和Random Forest 对人体乳腺肿瘤数据预测，利用10 折交叉验证的方法模拟实验，得到实验预测结果如表3。表3 为10折交叉验证得到的10 次结果。，表中看到随机森林（Random Forest）的准确率平均值达到了97.41%。

表3 ：Bagged CART 和Random Forest 的Accuracy 与Kappa 值对比

为数据集构建3个子模型（基学习器），Linear Discriminate Analysis (LDA) [线性分类器，类似的QDA]、Classification and Regression Trees (CART)、Support Vector Machine with a Radial Basis Kernel Function (SVM)。用相同的数据，得到3个模型的预测结果如表4。从表4 中可以看出3 个分类器中，svm 的结果最佳，精确率可以达到96.10%。

表4 ：三个分类器的分类后的Accuracy 与Kappa 值对比

将3 个模型的预测结果用简单线性模型组合子模型的预测结果精确率达到96.87%，高于96.10%。Kappa 值为0.9315531，模型的一致性很好。利用random forest 的stacking 得到了精确率为97.33%，kaapa 值为0.9417895。

3 结束语

机器学习集成方法应用前景较好，因为其较于单一模型实验效果准确率较高，比较于深度学习计算速度较快，所以在实际生活中很多领域都有应用，从上面的实验可以看出集成学习还可以与医学结合，结果良好。