高熵氧化物(MgCoNiCuZn)O热力学性能第一性原理研究

吴 睿 陈 瑜 慕玉浩 赵绪成

高熵氧化物(MgCoNiCuZn)O热力学性能第一性原理研究

吴 睿1陈 瑜2慕玉浩2赵绪成2

（1.广西产研院生物制造技术研究所有限公司，广西 南宁 530201；2.中国科技开发院广西分院，广西 南宁 530022）

高熵氧化物是近年来发展起来的氧化物材料体系，新型的高熵(MgCoNiCuZn)O晶体材料，是一种具有优异性能的单相高熵陶瓷材料，由于其机构中原子的无序性使得其在热电应用方面展现出优异的性能，在储能材料、电极材料等领域将有着广阔的应用前景，然而目前对于其制备的研究较多，但是对于热力学性质研究较少，热力学的研究主要描述物质的物理性质和热辐射之间的关联，具有高度的可靠性和普遍性，文章利用特殊准随机结构（SQS）建模，基于密度泛函理论第一性原理方法，采用准谐近似Debye-Grüneise模型，对该高熵氧化物(MgCoNiCuZn)O的热力学性质包括熵、体模量、热膨胀、等压热容、等温热容等进行了研究。

高熵氧化物；准谐德拜模型；第一性原理；特殊准随结构

引言

高熵合金（HEAs）[1]是近年来兴起的基于“高熵”理论，不同于传统一两种主元设计的一类新的合金材料新型材料，是合金功能材料研究领域的热点，一般由等摩尔比的5种或5种或以上元素完全无序组成的固溶合金，主要成份必须在5%～35%之间，比传统合金更优异的性能包括具有高强度、高硬度[1]、良好的结构稳定性[2]、热电性能[3]、优异的机械性能[4]、良好的抗腐蚀、抗氧化性能[5]等，具有高熵、迟滞扩散、严重的晶格畸变和鸡尾酒四种效应。

受高熵合金研究的启发，人们将高熵的研究理念进一步拓展到其他非金属材料中，包括氮化物[6]、碳化物[7]、硼化物[8]、氧化物[9]等方面，尤其对于多组分的单相固溶体高熵氧化物材料，被认为是最具有非常有前景的功能性材料。

高熵氧化物(MgNiCoCuZn)O（high entropy oxides，HEOs）是通过MgO, CoO, NiO, CuO, ZnO为初始原料均匀混合后，烧结而形成的新型单相固溶体高熵材料。由Rost等[9]于2015年初始制得。并通过研究发现该材料结构呈面心立方（FCC），同NaCl的结构相似，其中一个亚晶格中占据O阴离子，另一个亚晶格中被等原子比例随机排列的Mg, Co, Ni, Cu和Zn阳离子占据，且发现不同组元的物质的量的比对高熵氧化物的形成温度有着显著的影响，当这几种组元的物质的量相等时（即均为0.2时），形成单相固溶体所需温度最低；该高熵陶瓷烧结温度由高温向低温转变时，其相组成会发生可逆的变化，即会发生熵驱动下的可逆相变，由于高的构型熵对于材料单相的形成更有利，因此对于如所研究氧化物多组元系统来说，当组元数目越多、含量越接近时构型熵就越高，越容易形成单相固溶体，可以看出，在这种晶体材料中，熵对材料的热力学稳定性起至关重要的作用[10]。由于该高熵氧化物结构呈局域无序状，使得其热学、电学、磁学等功能特性展示出了优异的特性，例如在较宽的频率范围内具有较大的介电常数，在电化学阻抗谱测试时，由于氧空位的存在，以及电荷补偿机理，该化合物能够很容易掺杂Li+等碱金属离子，在电化学阻抗谱测试时，可表现出较强的离子传导性及巨大的介电常数；因而该氧化物作为超导材料将在新型电容储能器件和现代微电子领域得到广泛应用。

对于功能材料科学而言，材料热力学是重要的基础之一，主要研究材料的温度、体积、压力等宏观变量之间的关系，并描述物质的物理性质和热辐射之间的关联，可为许多的研究领域和工艺设计提供重要的理论依据，因此作为一种优良的热电材料，对其热力学的研究是必要的，然而目前对于其热力学研究较少。

本文采用特殊准随机结构（SQS）方法对所研究高熵氧化物建模，在基于密度泛函计算理论的支撑下，采用准谐近似德拜-格林乃森Debye-Grüneise模型的第一性原理[11]对所建高熵氧化物超胞模型进行优化计算，对高熵氧化物(MgCoNiCuZn)O的的热力学性能进行了研究，采用GIBBS2程序中的准谐近似Debye-Gruneisen模型进行研究以期对该材料工艺设计及应用得拓展提供理论依据。

1 理论与计算方法

1.1 热力学计算理论

本文热力学计算主要基于准谐德拜理论[11]。计算的关键是获得亥姆霍兹自由能F(V, T)对温度和/或体积的导数。F(V,T)可表示如下：

F(V,T)=E0K(V)+Fel(V,T)+Fvib(V,T)-TSconf(T) （1）

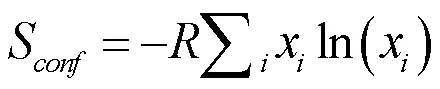
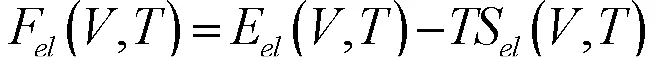
其中，Eel为电子热激发能，Sel为电子熵，分别可表示为：

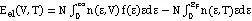
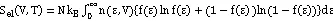
Fmag和Fvib分别为磁性自由能和振动自由能。对振动自由能的描述主要采用Debye-Grüneise模型进行研究，其计算方法如下：

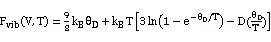
其中，kB为玻尔兹曼常数，D(θD/T)表示德拜函数。在准谐近似德拜模型中，德拜温度θD的依赖于体积，通过格林乃森（Grüneisen）参数γ来表示[13]。

通过在体积-温度函数中结合E0和Fel（V, T）来计算振动自由能Fvib（V, T），从而得到亥姆霍兹自由能面，继而求导就可以计算得到物质的体积模量、热膨胀系数、比热容、系统熵等宏观热力学性质。

1.2 计算方法

（1）超胞模型建立：采用特殊准随机结构（Special quasirandom structures，SQS）方法[14]模拟建立HEOs的超胞结构；

（2）优化弛豫方法：利用基于密度泛函理论的Vienna ab initio Simulation Package（VASP）[15]软件包进行第一性原理计算，其中Ecut为520 eV，k点设置为2×2×2，收敛标准为10-5eV/atom；

（3）离子-电子之间的相互作用：运用投影平面波势PAW来描述；

（4）交换关联函数计算：采用 PBE-GGA[16]方法计算；

（5）布里渊区取样积分：采用Monkhorst-Pack方案[17]进行，采用共轭梯度法进行几何优化[18]；

（6）数据拟合：采用Birch-Murnaghan EOS[19]拟合能量-体积（E-V）曲线获得平衡状态下的晶格参数；

（7）热力学参数：采用GIBBS2[20]程序中的准谐近似Debye-Gruneisen模型进行计算。

2 HEOs晶体结构优化

高熵氧化物HEOs是一种典型的面心立方（FCC）结构晶体，根据SQS建模方法，模拟生成了含有64个原子的2×2×2（每个晶胞含8个原子）的该氧化物超胞结构，如图1所示，其中该氧化物的镁、铜、钴、镍、锌等金属原子随机分布在在超胞的Wyckoff位置4a(0，0，0)处，非金属氧原子分布在超胞Wyckoff位置4b (1/2，1/2，1/2)处。

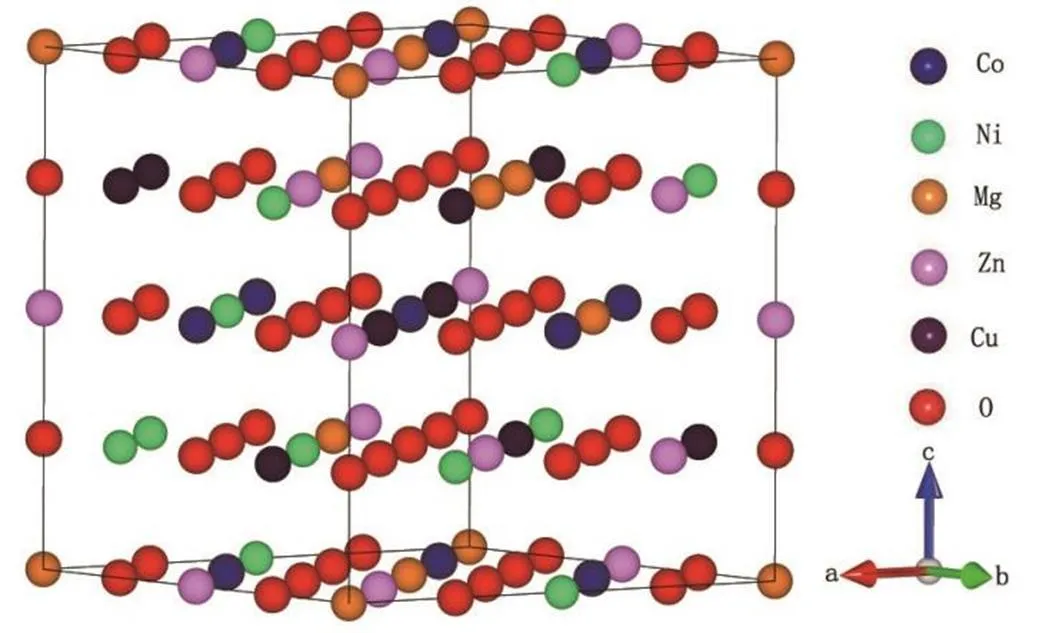
图1 高熵氧化物(MgCoNiCuZn)O的晶格结构

紧接着，对于模拟生成的超胞结构，运用GGA-PBE近似的密度泛函理论（DFT）进行计算，利用基于第一性原理计算的从头计算软件包对高熵氧化物HEOs进行充分优化，使其完全驰豫，从而得到基态下的晶体结构，然后对所得该化合物基态晶体结构施加V/V0步长为0.03的正负应变，并对施加应变后的晶体结构进行静态优化计算，从而得到该高熵氧化物HEOs的体积(Bohr3)与能量(Hartree)的函数关系，如图2所示。

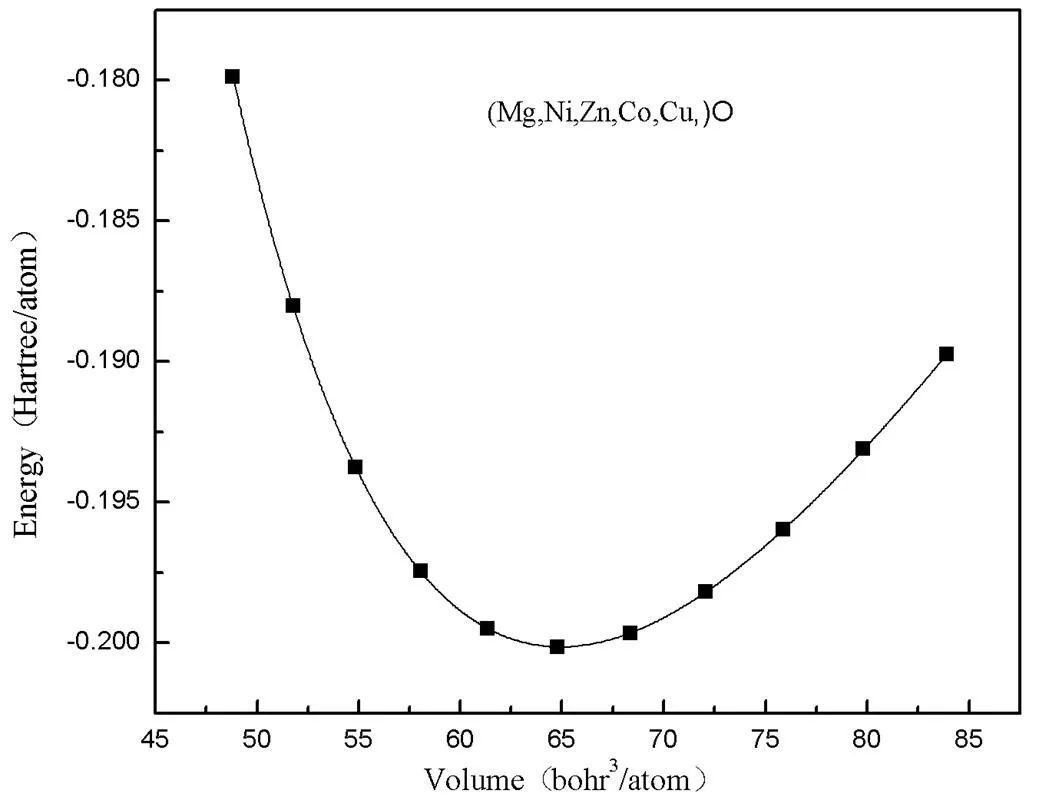
图2 计算得到HEOs的 E-V曲线

如上图，对计算得到的总能量E与体积V的11个数据点，利用三阶Birch-Murnaghan状态方程（EOS）进行拟合，从而得到其在基态下的晶格参数，其中晶格常数0=4.229，体模量B176.97，同五种亚组分二元氧化物晶格参数的平均值（0=4.223，0=178）相比，结果比较接近，可见所研究的HEOs材料同大多数高熵材料一样，均近似遵循混合规律，表明该材料已形成了单相固溶体。

3 HEOs晶体热力学性质

根据高熵氧化物HEOx的热稳定性，选取了0 K～1000 K温度范围，研究了该晶体材料熵、体模量、热容、德拜温度等热力学性质。

3.1 熵

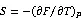
图3 HEOs的熵S（a）和振动熵（b）电子熵Sel（c）随温度的变化曲线

3.2 体积模量B

体模量通常定义了材料在外部压缩条件下抵抗体积变化的能力，()[dF/dV]，研究了HEOs体模量随温度的变化，计算结果如图4所示。

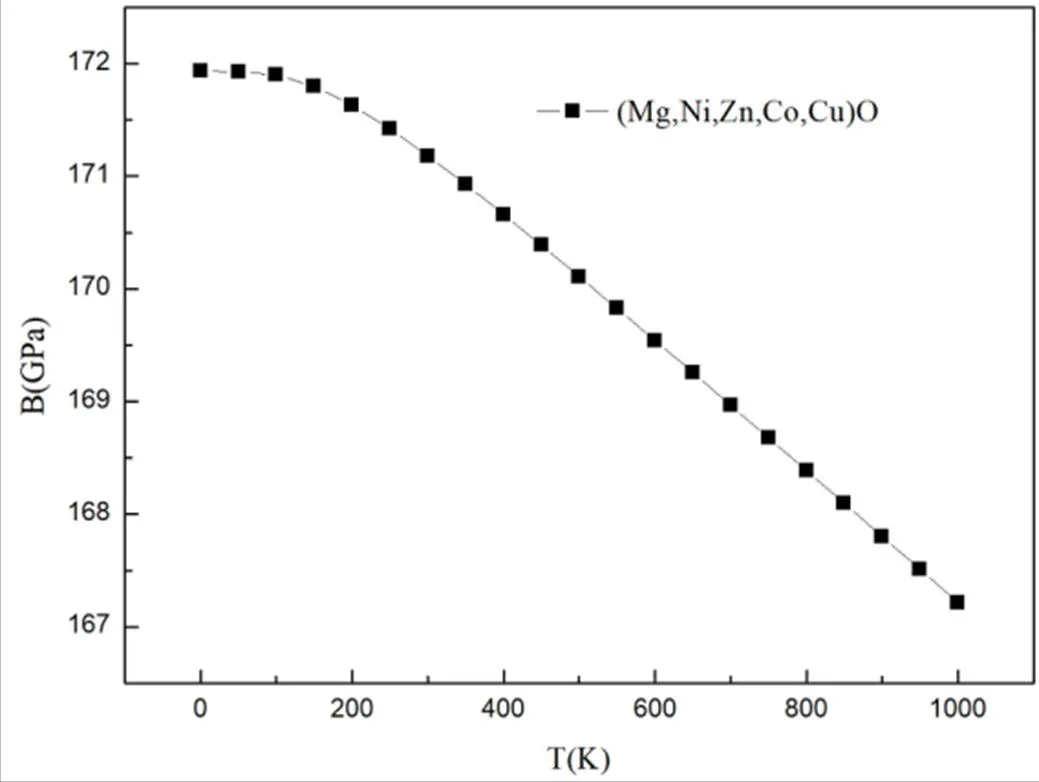
图4 HEOs的体模量B随温度的变化曲线

从图中可以发现，随着温度的升高，三者的体模量变化相似均随温度升高而下降，表明该材料大体上都呈现软化趋势，在＜100 K时变化不大，在100 K以上时下降幅度逐渐增大。

3.3 热膨胀

材料的热膨胀通常用体积的温度依赖性来描述，计算所得的高熵氧化物HEOs的体积随温度的变化如图5（a）所示。可以看出，该材料体积都随温度升高呈现出变大的趋势。当温度低于～300 K时，体积随温度的升高而缓慢增加，当温度高于～300 K时，体积增加幅度变大。但该氧化物的体积变化率相差不大。

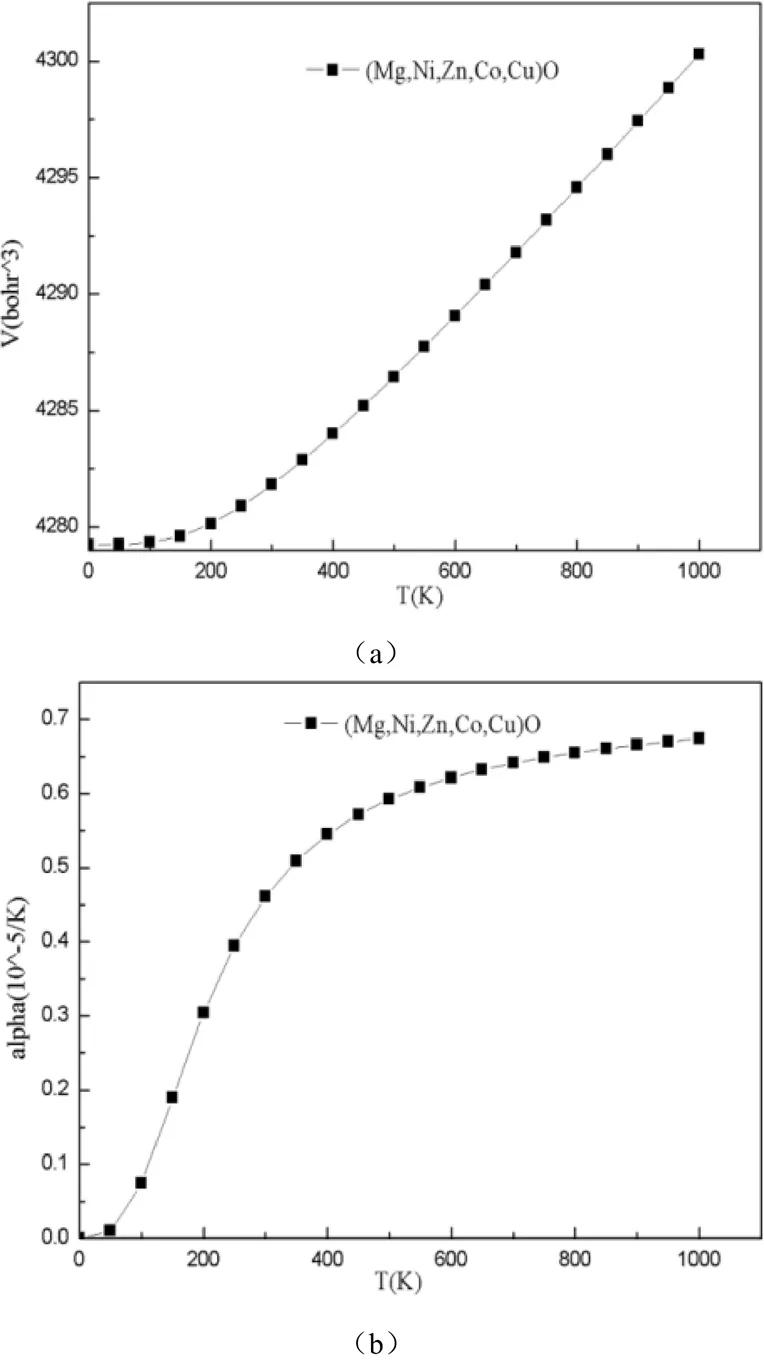
图5 HEOs的体积V（a）和热膨胀系数α（b）随温度的变化曲线

材料体积随温度的热膨胀通常用也用热膨胀系数来描述，本文基于方程()/研究HEOs的热膨胀系数随温度的变化情况。计算结果如图5（b）所示。可以看出，该材料的热膨胀系数随温度的变化规律是基本相似的。当温度在～300 K以下时，热膨胀系数随温度的升高呈逐渐增大趋势，而温度越高，热膨胀系数的增大趋势越平缓。热膨胀系数与热容密切相关，并与热容有着相似的规律。即在低温时，膨胀系数也像热容一样按3规律变化。

3.4　热容

热容反映了材料储热的能力。表达式是C = T()，该高熵氧化物HEOs的C随温度的变化情况如图6（a）所示，当＜～500K时，C随温度升高快速增加，同3呈正比例增长。当＞500K时，C值近似为一个常数，满足著名的杜隆-珀蒂极限（C = 3，其中为单胞的原子数）[20]。

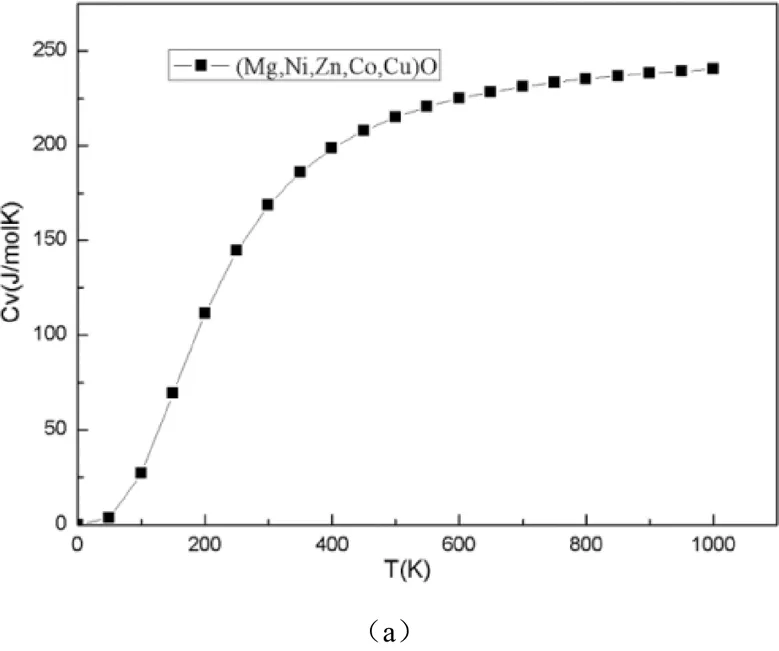
等压热容C随温度的变化趋势如图6（b）所示，显然同C一样表现出类似的变化趋势。在低温下＜～500 K，C的值快速增加，当＞～400 K后随着温度的升高而缓慢增加。

3.5　德拜温度和格林乃森参数

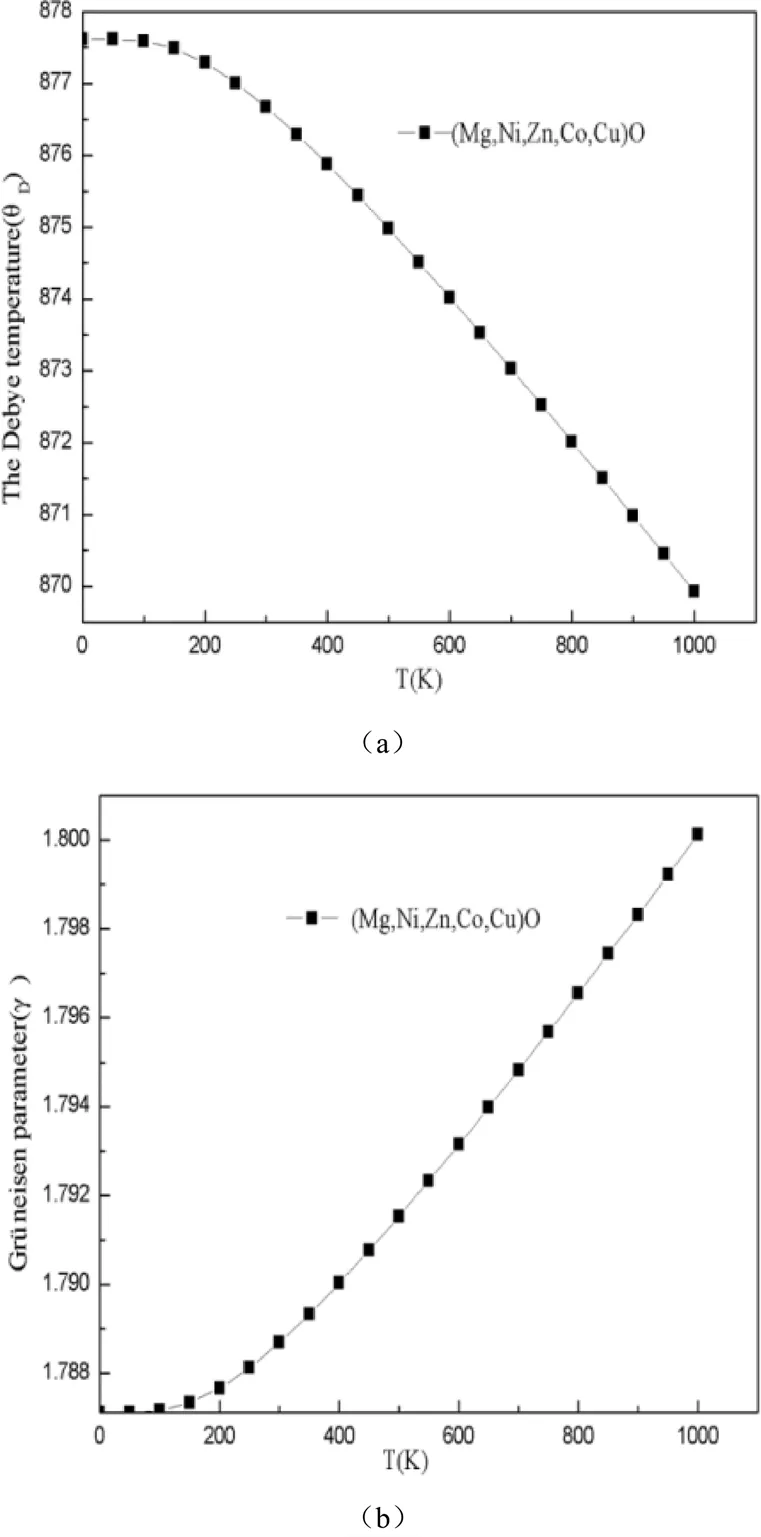
图7 HEOs的德拜温度θD（a）和格林乃森参数γ（b）随温度变化曲线

根据格林乃森参数表达式=-(dln)/(dln)，研究了HEOs在不同温度下的德拜温度θ的变化趋势，计算结果如图7(b)，可见都随温度升高而缓慢增加。由于材料的γ值可以根据=VαB/C公式来评估，从目前的结果表明，温度对该高熵氧化物格林乃森参数的影响是不显著的。

4　结论

本文基于准谐近似德拜-格林乃森Debye-Gruneisen模型，采用第一性原理计算方法，并结合特殊的准随机结构（SQS）建模，对高熵氧化物陶瓷材料（MgCoNiCuZn)O的热力学性质进行了研究，研究发现，该陶瓷材料晶格参数同实验值吻合，表明其形成了固溶体；是热力学稳定的，该材料系统熵主要来源于振动熵贡献，且均随温度的升高而明显增大，随着温度的升高，体模量下降，热膨胀系数温度在～300 K以下时，随温度的升高呈逐渐增大趋势，而温度越高，热膨胀系数的增大趋势越平缓，等容和等压热容均在低温时随温度增大呈直线上升，当温度大于～500 K时，等容热容值近似为一个常数，满足著名的杜隆-珀蒂极限；温度对这该材料的德拜温度和格林森参数影响比较小。材料导热性能较好。

[1]Braic V, Vladescu A, Balaceanu M, et al. Nanostructured multi-element (TiZrNbHfTa)N and (TiZrNbHfTa)C hard coatings[J]. Surface and Coatings Technology, 2012, 211(42): 117-121.

[2]Zhao Y J, Qiao J W, Ma S G, et al. A hexagonal close-packed high-entropy alloy: The effect of entropy[J]. Materials and Design, 2016, 96: 10-15.

[3]Nong Z S, Zhu J C, Zhao R D. Prediction of structure and elastic properties of AlCrFeNiTi system high entropy alloys[J]. Intermetallics, 2017, 86: 134-146.

[4]Nong Zhi Sheng, Zhu Jing Chuan. Prediction of structure and elastic properties of AlCrFeNiTi system high entropy alloys[J]. Intermetallics, 2017, 86: 134-146.

[5]Tsai M H, Yeh J W. High-Entropy Alloys: A Critical Review[J]. Materials Research Letters, 2014, 2(3): 107-123.

[6]Jin Tian, Sang Xia, Unocic R R, et al. Mechanochemical- assisted synthesis of high-entropy metal nitride via a soft urea strategy[J]. Advanced Materials, 2018, 30(23): 1707512.

[7]Castle E, Csanádi T, Grasso S, et al. Processing and properties of high-entropy ultra-high temperature carbides [J]. Scientific Reports, 2018, 8(1): 8609.

[8]Gild J, Zhang Y, Harrington T, et al. High-entropy metal diborides: A new class of high-entropy materials and a new type of ultrahigh temperature ceramics[J]. Scientific Reports, 2016, 6(1): 37946.

[9]Rost C M, Sachet E, Borman T, et al. Entropy-stabilized oxides[J]. Nature Communications, 2015, 6: 8485.

[10] Huang C, Zhang Y, Rui V, et al. Dry sliding wear behavior of laser clad TiVCrAlSi high entropy alloy coatings on Ti-6Al-4V substrate[J]. Materials and Design, 2012, 41: 338-343.

[11] Otero-De-La-Roza A, Abbasi-Pérez D, Luaña V. GIBBS2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation [J]. Computer Physics Communications, 2011, 182(10): 2232-2248.

[12] Bérardan D, Franger S, Meena A K, et al. Room temperature lithium superionic conductivity in high entropy oxides[J]. Journal of Materials Chemistry A, 2016, 4(24): 9536-9541.

[13] Blöchl P E. Projector augmented-wave method[J]. Physical Review B, 1994, 50(24): 17953-17979.

[14] Blanco M A, Francisco E, Luaña V. GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model[J]. Computer Physics Communications, 2004, 158(1): 57-72.

[15] Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J]. Computational Materials Science, 1996, 6(1): 15-50.

[16] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865-3868.

[17] Chadi D J. Special points for Brillouin-zone integrations[J]. Physical Review B Condensed Matter, 1977, 16(4): 5188-5192.

[18] Shewchuk, Jonathan R. An introduction to the conjugate gradient method without the agonizing pain[J]. Journal of Comparative Physiology, 1994, 186(3): 219-220.

[19] Birch F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300℃[J]. Journal of Geophysical Research Solid Earth, 1978, 83(B3): 1257-1268.

[20]Otero-De-La-Roza A, Abbasi-Pérez D, Luaña V. GIBBS2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation[J]. Computer Physics Communications, 2011, 182(10): 2232-2248.

First Principle Study on Thermodynamic Properties of (MgCoNiCuZn)O High-Entropy Oxides

High entropy oxide is an oxide material system developed in recent years. A new type of high entropy (MgCoNiCuZn) O crystal material is a single-phase high entropy ceramic material with excellent performance. Due to the disorder of atoms in its mechanism, it shows excellent performance in thermoelectric applications and will have broad application prospects in energy storage materials, electrode materials and other fields. At present, there are many studies on its preparation, however, there is little research on thermodynamic properties. Thermodynamic research mainly describes the correlation between physical properties of substances and thermal radiation, which is highly reliable and universal. This paper uses special quasi random structure (SQS) modeling, based on the first principle method of density functional theory, and adopts Quasi-harmonic approximate Debye-Grüneisen model to study the thermodynamic properties of this high entropy oxide (MgCoNiCuZn) O, including entropy, bulk modulus, thermal expansion isobaric heat capacity and isothermal heat capacity were studied.

high-entropy oxides; Quasi-harmonicDebye-Grüneisen model; first principle; special quasi-random structures

TQ12

A

1008-1151(2022)08-0047-05

2022-04-26

吴睿（1982－），男，广西产研院生物制造技术研究所有限公司高级工程师，博士，研究方向为生物化工、化工工艺。