黔西北垭都—蟒硐成矿带构造分形结构特征及找矿意义

崔中良，姚艳领，程金华，罗 开，周家喜,

1. 江西应用科技学院 光华宝石矿物资源学院, 南昌 330100；

2. 云南建投第一勘察设计有限公司，昆明 650000；

3. 诸暨市自然资源和规划局，绍兴 312000；

4. 云南大学 地球科学学院，昆明 650500；

5. 云南省高校关键矿产成矿学重点实验室，昆明 650500

分形理论自20世纪70年代Mandelbrot创立以来（Mandelbrot, 1975），便在非线性领域得到迅速发展和广泛应用（Barton et al., 1995; Cheng, 1995;Turcotte, 2002; Xie et al., 2010; 张瑞忠等, 2018; 朱平平等, 2020）。在建筑材料性能表征（宋宇等,2020; Alireza et al., 2012）、土力学（孙超等, 2020;彭子茂和黄震, 2020）、岩石力学（赵晓彦等,2020）、地质灾害（Pourghasemi et al., 2014; 王潇等,2019; 施国栋等, 2020a）、水系结构（Donadio et al.,2013; 孟宪萌等, 2019）、断裂定量表征（廖家飞等,2012; 赵少攀等, 2015; 孙涛等, 2018）和成矿规律及找矿预测（Cheng, 1995; 卢新卫和马东升, 1999;宋保昌等, 2002; 丁式江, 2004; 张建等, 2009; Xie et al., 2010; 李飞等, 2016; 施国栋等, 2020b）等领域，分形理论都有很好的应用实例。断裂构造（卢新卫和马东升, 1999; 廖家飞等, 2012; 赵少攀等,2015; 孙涛等, 2018）、矿床储量（Mandelbrot, 1983;Turcotte, 2002; 蒋成竹等, 2012）、矿床空间分布（张建等, 2009; 韩喜彬等, 2010; 施国栋等, 2020b）等均具有分形特征，这为分形理论应用于构造与成矿关系研究奠定了理论基础。

川滇黔接壤铅锌矿集区是中国重要的铅锌资源基地（Zhou et al., 2018），黔西北铅锌成矿区是该矿集区的重要组成部分（周家喜等, 2009）。黔西北铅锌成矿区按成矿构造带可划分为垭都—蟒硐、威宁—水城和银厂坡—云炉河坝等三个主要成矿带（周家喜等, 2010），其中垭都—蟒硐成矿带具有铅锌矿床（点）数量多（吴大文等, 2019）、规模大（金中国, 2006; 邓克勇等, 2007; 周家喜等,2012; 魏本赞等, 2019）、构造分级控矿特点显著（金中国, 2006; 韩润生等, 2020）等特征。随着猪拱塘特大型铅锌矿床的发现（何良伦等， 2019a），垭都—蟒硐成矿带显示出巨大的找矿潜力。尽管众多学者应用各种方法对该成矿带进行了深入的成矿理论和找矿方法研究，但垭都—蟒硐成矿带构造分形研究及其找矿应用少有涉及。分形理论能够精细描述复杂结构以及定量化揭示隐藏的规律性（张建等,2009），有助于定量解析构造分形结构特征，结合构造控矿特征及Fry分析，还可以为进一步找矿预测指明方向。基于此，本文在垭都—蟒硐成矿带构造分形结构特征解析的基础上，采用Fry分析方法（Fry, 1979; 黄继钧和李亚林, 2007; Austinet et al.,2009; Carranza, 2009），剖析成矿带内铅锌矿床（点）的分布规律，结合成矿带内构造组合控矿样式，探讨进一步找矿方向，以期为研究区资源勘查工作提供有益线索。

1 地质概况

黔西北垭都—蟒硐成矿带位于扬子板块西南缘（图1；金中国和黄智龙, 2008; 韩润生等, 2020），是垭都—紫云深大断裂的一部分。垭都—紫云断裂南与师宗—弥勒断裂、西与小江断裂界定了川滇黔接壤铅锌矿集区主体范围（何良伦等, 2019a）。垭都—蟒硐成矿带整体呈NW向展布，带内出露地层由老至新主要有志留系、泥盆系、石炭系、二叠系和三叠系，岩性以白云岩、白云质灰岩和灰岩为主（周家喜等, 2012）。泥盆纪以后成矿带内以海相碳酸盐岩沉积为主，海陆交互相及陆相碎屑岩沉积次之（蔡国盛等, 2020）。成矿带区内岩浆岩主要见玄武岩和辉绿岩（何良伦等, 2019b; 金中国, 2006）。垭都—蟒硐成矿带主要控矿构造是垭都—蟒硐构造带（何良伦等, 2019a; 韩润生等,2020），其整体构造行迹呈NW向，由一系列叠瓦状逆冲断层、背斜及NE向次级断层构成（蔡国盛等, 2020）。垭都—蟒硐构造带具有多期活动特点，早期控岩、控相，晚期控矿（金中国, 2008;何良伦等, 2019a）。垭都—蟒硐成矿带目前发现44个铅锌矿床（点）（图1），其中（特）大型矿床1个（猪拱塘），中型矿床5个（五里坪、天桥、猫榨厂、筲箕湾和板板桥），小型矿床23个。这些铅锌矿床（点）均分布于NW向垭都—蟒硐构造带内（韩润生等, 2020），赋矿围岩为碳酸盐岩。研究表明，垭都—蟒硐成矿带内的铅锌矿床（点）成因类型属于低温热液型（金中国, 2006; 邓克勇等, 2007; Zhou et al., 2018; 魏本赞等, 2019），是流体混合—构造组合—岩性组合耦合成矿的产物（Zhou et al., 2018）。

图1 垭都—蟒硐成矿带断裂构造及矿床（点）分布图（据蔡国盛等, 2020修改）Fig. 1 Map showing the fracture structure and deposit (point) distribution of the Yadu-Mangdong metallogenic belt

2 断裂构造空间展布分形结构

2.1 计算方法及原理

（1）容量维D0

目前线性构造容量维的计算方法较多，本文以垭都—蟒硐成矿带断裂构造及矿床（点）分布图为底图，采用应用最为广泛的的计盒维数法进行计算。计盒维数法进行分形计算的思路为：采用不同边长r（r=L，L/2，L/4，L/8…，为一首项为正数、公比等于0.5的等比数列）的正方形格子去覆盖研究区，分别计算覆盖到断层的网格数N(r)，若N(r)与r满足如下幂定律关系（式①），则研究对象为分形。

其中C、D0为常数。将式①两边分别取对数得式②，由式②可知若lnN(r)与lnr为线性关系，则研究对象为分形，分维值D0即为该线性关系式斜率的绝对值。

具体步骤如下：（1）分别采用边长为26.965 km、13.483 km、6.741 km、3.371 km的二维正交网格覆盖研究区，并分别统计总体构造、NW向构造覆盖到断层的网格数N(r)。在Excel中以以lnr为横轴，以lnN(r)为纵轴，分别绘制不同类型构造的回归拟合直线，得到不同类型构造的分维值。（2）将边长r为13.483 km的二维正交网格进行编号分区，分区结果如图2所示。对于每个分区，分别以边长6.741 km、3.371 km的二维正交网格覆盖，并统计分区总体构造覆盖的网格数N(r)。利用Excel绘制回归拟合直线，得到分区总体构造的分维值。

图2 研究区分维值计算分区图（据蔡国盛等, 2020修改）Fig. 2 Grid map of fractal dimension calculation

（2）信息维D1

断层信息维不仅考虑二维网格是否有断层穿越，而且也考虑二维网格内穿越断层的条数（或概率）。将研究区覆盖边长为r的二维正交网格，假定将构造分割成了N(r)份，若断裂构造出现在第i个正交网格的概率为Pi(r)（式③），则这时的总信息量为I(r)（式④）。

变换二维正交网格的边长r，若I(r)与lnr之间存在如下线性关系（式⑤），则可由直线的斜率求出信息维数D1。

具体步骤如下：（1）分别采用边长为26.965 km、13.483 km、6.741 km、3.371 km的二维正交网格覆盖研究区，并分别计算总体构造、NW向构造的信息量I(r)。在Excel中以以lnr为横轴，以I(r)为纵轴，分别绘制不同类型构造的回归拟合直线，得到不同类型构造的分维值。（2）对于每个分区，分别以边长6.741 km、3.371 km、1.685 km的二维正交网格覆盖，并统计分区总体构造的信息量I(r)。利用Excel绘制回归拟合直线，得到分区总体构造的分维值。

2.2 断裂构造整体分形特征

垭都—蟒硐成矿带断裂构造分维值计算参数统计见表1，根据表1中的统计参数绘制出研究区整体断裂构造及NW向断裂构造分维值计算线性拟合图（图3）。从图3可以看出4条回归拟合直线的判定系数（拟合度）R2分别为0.9983、1.0000、0.9958、0.9965，最小为0.9958，直线的拟合程非常高，说明了在研究标度3.371~26.965 km范围内，研究区内断裂构造具有很好的统计自相似性。研究区断裂构造绝大多数为NW向，说明NW向断裂的分维值（容量维、信息维）大于NE向断裂的分维值（容量维、信息维），即全区断裂构造分维值（容量维、信息维）＞NW向断裂构造分维值（容量维、信息维） ＞NE向断裂构造分维值（容量维、信息维）。

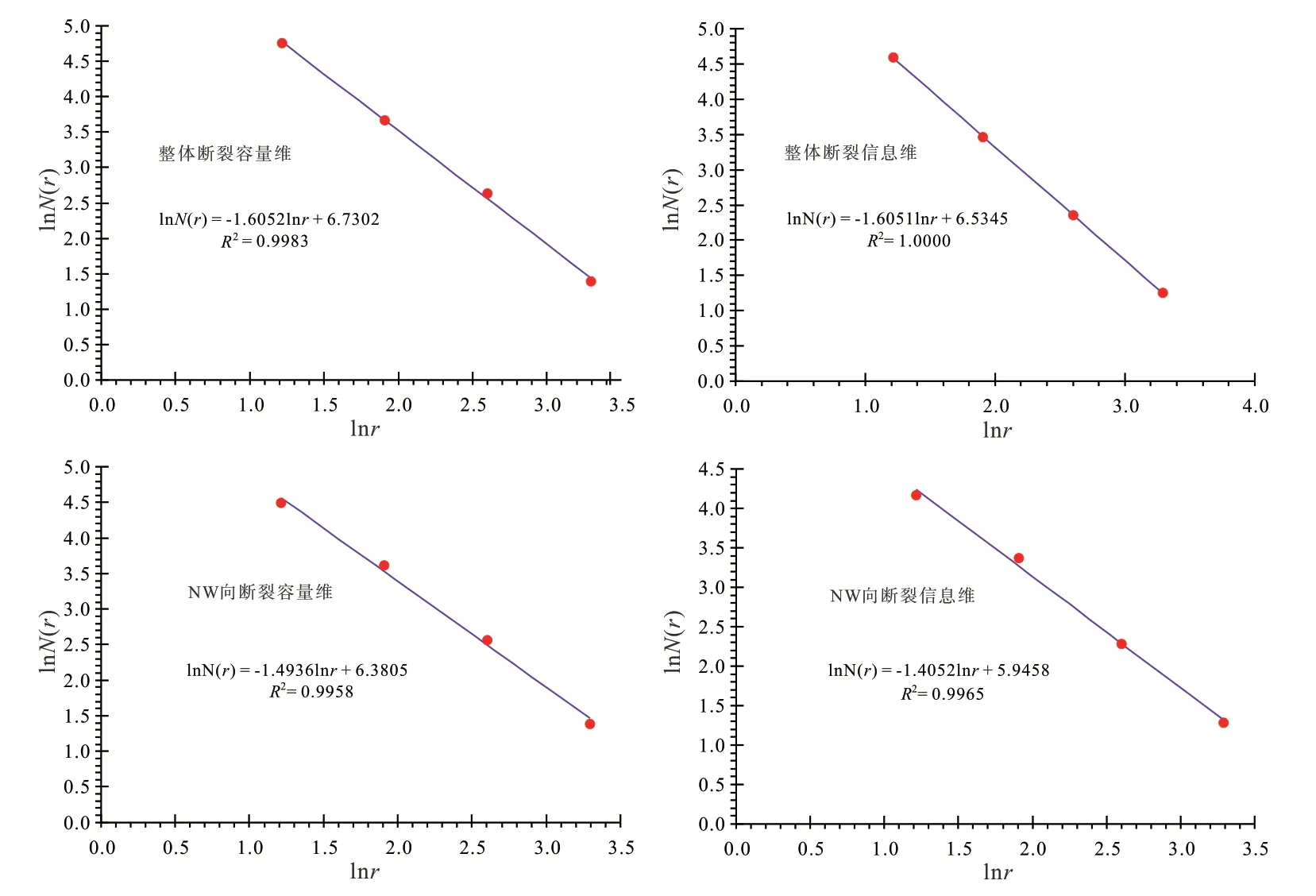
图3 研究区断裂构造分维值计算线性拟合图Fig. 3 Linear fitting of fractal dimension calculations of fault structures in the study area

表1 垭都—蟒硐成矿带断裂构造分维值计算参数统计表Table 1 Calculation parameters of fractal dimension for fault structure in the Yadu-Mangdong metallogenic belt

研究区整体断裂容量维为1.6052，信息维为1.6051，NW向断裂容量维为1.4936，信息维为1.4052，两者相应的分形维数数值极为接近，反映了研究区整体断裂以NW向为主导，这与区域构造特征相吻合。已有的研究成果（卢新卫和马东升, 1999; 丁式江, 2004; 谢焱石和谭凯旋, 2002; 成永生, 2010; 廖家飞等, 2012; 赵少攀等, 2015; 李飞等, 2016; 孙涛等, 2018）表明，断裂构造分维值与断裂（地质体）连通性相关，即随着断裂构造分维值的增大，断裂构造的空间分布愈来愈复杂，断裂（地质体）的渗透性就越来越强，连通性就越来越好，从而愈有利于成矿元素的活化及成矿流体的运移、聚集。从中国部分地区断裂构造分维值统计表（表2）来看：（1）垭都—蟒硐成矿带容量维大于云贵活动区、川滇黔接壤铅锌矿集区、赣南地区、诸广地区、招远金矿矿集区、青海虎头崖多金属矿集区、中国大陆克拉通等地区，小于湖南南部骑田岭矿集区、湘中地区，与桂东南金银成矿区相近，处于中国大陆活动区分维值之间。（2）垭都—蟒硐成矿带整体断裂信息维小于湘中锡矿山—龙山锑矿带、湘中四明山锑矿带和湘中地区信息维，与湘中大神山锑矿带信息维相近。（3）垭都—蟒硐成矿带北西向断裂容量维大于云贵活动区、川滇黔接壤铅锌矿集区NW向断裂、赣南地区、诸广地区、青海虎头崖多金属矿集区、中国大陆克拉通等地区，与招远金矿矿集区容量维相近，处于中国大陆活动区分维值之间。（4）垭都—蟒硐成矿带整体断裂及NW向断裂分维值均远大于断裂分维临界值1.22~1.38 （Kruhl, 1994）。因此，垭都—蟒硐成矿带断裂构造十分复杂，具有优越的成矿构造背景。研究区NW向断裂与整体断裂相应分维值十分接近，从断裂构造分维值的地质意义来看，NW向断裂复杂程度亦很高，发育成熟度和连通性都很好，对区域上流体运移成矿的贡献很大，也即说明NW向断裂构造体系对区内矿床（点）的分布起主导作用。这与区内矿床（点）多沿NW向断裂分布的地质事实相吻合。

表2 中国部分地区断裂构造分维值统计表Table 2 Fractal dimensions of fault structures in some areas of China

2.3 断裂构造分区分形特征

2.3.1 容量维

垭都—蟒硐成矿带分区容量维计算参数统计见表3。根据表3可知分区分维值拟合直线判定系数（拟合度）0.9643~1.0000，直线的拟合度非常高，说明了分区内断裂构造具有很好的统计自相似性。分区容量维1.0000~1.9534，中位数1.5426，平均值1.5529。因断裂分维临界值为1.22~1.38（Kruhl，1994），本文把1.22、1.38作为分区容量维分组的重要节点。12个分区中，容量维＜1.22的分区2个，容量维1.22~1.38的分区3个，容量维＞1.38而＜1.54的分区1个，容量维≥1.54的分区6个。

表3 分区容量维计算参数统计表Table 3 Partition capacity dimension calculation parameters

2.3.2 信息维

垭都—蟒硐成矿带分区信息维计算参数统计见表4。根据表4可知分区分维值拟合直线判定系数（拟合度）0.9828~0.9998，直线的拟合度非常高，亦说明了分区内断裂构造具有很好的统计自相似性。分区信息维0.9702~1.7781，中位数1.4662，平均值1.4187。

表4 分区信息维计算参数统计表Table 4 Calculation parameters of partition information dimension

3 矿床（点）/资源量空间分布分形丛集结构

为定性阐明矿床（点）分布丛集性，统计垭都—蟒硐成矿带各分区矿床（点）及金属资源量发育情况（表5）。从表5可知：（1）大型矿床共计1个，分布于分区6。（2）中型矿床共计5个，分布于分区5、分区6、分区7和分区11。（3）小型矿床共计23个，主要分布于分区7、分区10、分区6、分区5和分区11。（4）矿点共计15个，分布于分区7、分区6、分区10和分区11。综上所述，12个分区中，矿床（点）主要分布于分区6、分区5、分区11、分区7和分区10，金属资源量与矿床（点）分布一致，矿床（点）及金属资源量丛集性显著。

表5 分区矿床（点）分布及金属资源量统计表Table 5 Deposits (points) distribution and metal resources

3.1 资源量分布分形丛集结构

为实现定量描述资源量分布的丛集性，采用频数—大小分形模型进行表征。频数—大小分形模型为（Mandelbrot，1983）：

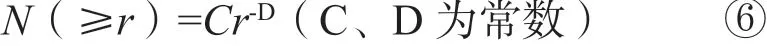
本文将r定义为矿床储量，则N（≥r）代表研究区中储量不小于r的矿床个数。将式⑥两边分别取对数得式⑦，由式⑦可知若lnN（≥r）与lnr为线性关系，则研究对象为分形，分维值D即为该线性关系式斜率的绝对值。

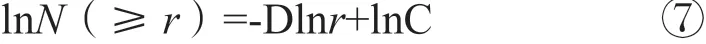
基于垭都—蟒硐成矿带30个矿床金属资源量的大小分布特征，结合矿床储量规模划分原则，式②中矿床储量r取值2、4、6、8、10、50。频数—大小分形模型重要参数统计见表6。

根据表6参数绘制lnr-lnN（≥r）回归拟合直线图（图4），分维值为0.9313，拟合度R2为0.9638，说明研究区资源量分布呈分形丛集结构。

图4 资源量空间分布分维值计算线性拟合图Fig. 4 Linear fitting of fractal dimension calculation and spatial distribution of resources

表6 频数—大小分形模型重要参数统计表Table 6 Important parameters of frequency size fractal model

3.2 矿床（点）空间分布分形丛集结构

把矿床当做空间上的点集，运用计盒维数法即可定量表征矿床（点）空间分布分形丛集结构。矿床空间分布分维值计算参数统计见表7，根据表7绘制lnr-lnN（r）回归拟合直线图（图5）。从图5可以看出：（1）矿床（点）、小—大型矿床、中—大型矿床线性拟合直线的拟合度均大于0.96，说明矿床（点）、小—大型矿床、中—大型矿床空间分布为分形丛集结构。（2）矿床（点）分布分维值＞小—大型矿床分布分维值＞中—大型矿床分布分维值。（3）小—大型铅锌矿床空间分布分维值为1.0096，极为接近于一条直线的容量维1，说明矿床分布有一个明显优势方位，这与NW向垭都—蟒硐构造带整体控制矿床（点）空间分布的地质事实相吻合，优势方位即为NW向。（3）矿床分布的丛集性会导致矿床分维值降低，而研究区矿床空间分布分维值远小于研究区整体断裂及NW向断裂容量维，一定程度上说明了矿床空间分布丛集性较强。

图5 不同规模铅锌矿床空间分布分维值计算线性拟合图Fig. 5 Linear fitting of fractal dimension calculation and spatial distribution of ore deposits of different sizes

表7 矿床分布分维值计算参数统计表Table 7 Calculation parameters of fractal dimension of deposit distribution

4 断裂分维值与矿床（点）分布耦合规律

前已述及，断裂分维值可以表征断裂连通性，即断裂分维值越大，则其连通性越好。那么断裂分维值相对较低的分区连通性也相对较差，亦可起到相对的阻挡作用，并把流体流动相对的局限于骨干断层中，增加含矿流体的局域化分布。为研究这种作用对矿床分布的影响，并描述发育矿床分区出现的位置，假设分区分维值横向波动及纵向波动是连续的，根据表2、3、4用曲线绘制分区分维值横向、纵向变化图（图6）。根据各个分区的整体分维值（容量维、信息维）绘制分区分维值与矿床规模关系图（图7）。

图6 分区分维值横纵波动图Fig. 6 Vertical and horizontal wave graphs of fractal dimensions

图7 分区分维值与矿床发育规模、频数关系图Fig. 7 Relationship between fractal dimension and deposit development scale and frequency

根据表5、图6和图7可以看出：（1）小型铅锌矿床发育于容量维大于1.29、信息维大于1.39的分区，中—大型铅锌矿床发育于容量维大于1.58、信息维大于1.42的分区，也即说明发育中—大型铅锌矿床分区的分维值区间较窄，分维值较高。铅锌矿床有利分布区即为容量维大于1.58、信息维大于1.42的地区。（2）分布矿床分区分维值在波动中主要处于较大值位置，说明存在至少一个分维值相对较小邻区（横向或纵向方向）的分区，即存在相对阻挡、封闭流体区的分区，有利于发育矿床。实际上，由于矿床分布的丛集性，往往连续2个甚至更多分区发育矿床，这时就需要将这些分区看成一个整体，从而认识构造阻挡、封闭成矿流体的作用。例如把发育较多铅锌矿床的5、6、7、10和11分区看成一个整体，那么根据其与邻区容量值或信息维的相对大小，可把其相邻的6个分区均可看作流体相对封闭区。

根据各个分区的整体分维值（容量维、信息维）及各分区中心坐标（自行设立相对坐标系）绘制分维值等值线图（图8）。图8中分区中心分维值即为分区的整体分维值。从分维值等值线图可以看出，研究区中—大型矿床及绝大多数小型铅锌矿床都分布于分维值较高地区（浅灰色区域），说明矿床空间分布与分维值有很好的耦合关系，亦能看出分维值等值线展布趋势与NW向构造线方向基本吻合。

图8 分维值等值线图Fig. 8 Contours of fractal dimensions

5 找矿方向探讨

5.1 分维值分析

从分维值的角度来看，矿床分布的有利区应满足两个条件：（1）分维值较高。铅锌矿床有利分布区为容量维大于1.58、信息维大于1.42的地方。（2）存在相对阻挡、封闭流体区的邻区。根据以上两点圈定找矿有利区（图9），有利区呈NW向不规则的条带状。

5.2 控矿构造

从垭都—蟒硐成矿带典型矿床控矿构造特征来看，带内矿床的主控断裂以NW向为主，组合样式以断层—背斜组合式为主（表9）。因此，从构造控矿的角度来看，带内重点找矿方向应以同时发育NW向断裂及背斜的区域为主。

表9 研究区典型矿床控矿构造特征Table 9 Characteristics of ore controlling structures of type deposits in the study area

5.3 Fry分析

Fry分析也即全心距离法分析，由Fry（1979）提出，具有简便快速的分析优势，最早用于研究随机点的空间分布和岩石在不同方向上应力比的测量（Fry, 1979），随后被广泛应用于矿床空间分布的度量及潜在控矿构造的推断（Ghaleb et al., 1995;Yaghubpur et al., 2006; Austin et al., 2009; Carranza et al., 2010; Parsa et al., 2018）。本文运用Fry分析, 研究已知矿床空间分布规律并探索未知矿床可能分布的地方。根据分维值圈定的有利成矿区空间展布优势方位为NW向，而从Fry矿床（点）分析结果（图9）来看，矿床（点）分布整体优势方位亦为NW向，与研究区主要控矿构造垭都—蟒硐断裂带的展布方向一致。根据矿床分布特征，划分了3个有利成矿区：（1）1号和2号有利成矿区均为小—大型矿床有利成矿区，其中1号有利成矿区内矿床分布的优势方位为NW向，2号有利成矿区矿床分布的优势方位为NE向；（2） 3号有利成矿区是小型、中型矿床有利成矿区，区内矿床分布的优势方位为NW向。

图9 分维值有利成矿区Fig. 9 Fractal dimension showing favorable areas for mining

5.4 找矿方向

研究区有利成矿区主要根据分维值、构造控矿特征和Fry分析等综合研究确定，并依据有利成矿区的重要程度划分为四个级别（图10）。Ⅰ级有利成矿区为分维值分析有利成矿区、Fry分析有利成矿区、控矿构造组合样式有利成矿区等三部分公共的叠合部位，空间上呈NW向展布，找矿潜力最大。除Ⅰ级有利成矿区外，分维值分析有利成矿区、Fry分析有利成矿区、控矿构造组合样式有利成矿区等两两重合部位即为Ⅱ级有利成矿区，共计两个区域，空间上呈NW向展布，找矿潜力次之。Ⅲ级有利成矿区为除Ⅰ级、Ⅱ级有利成矿区外，分维值分析有利成矿区、控矿构造组合样式有利成矿区的剩余区域，空间上主要分布于Ⅰ级、Ⅱ级有利成矿区的边部，找矿潜力第三。Ⅳ级有利成矿区为Fry分析有利成矿区的剩余区域，均位于Ⅱ级有利成矿区的边部，找矿潜力较小。

图10 矿床（点）Fry分析图Fig. 10 Fry analysis diagram of deposit（spot）

图11 综合分析有利成矿区Fig. 11 Comprehensive analysis of favorable ore-forming areas

6 结论

在研究区3.371～26.965 km范围内，断裂构造具有很好的统计自相似性。研究区整体断裂容量维为1.6052，信息维为1.6051，而NW向断裂容量维为1.4936，信息维为1.4052，两者相应的分形维数数值极为接近，反映了研究区整体断裂以NW向为主。

铅锌矿床分布区具有分维值较高和存在相对阻挡—圈闭流体区两个特征，其中小型铅锌矿床发育于容量维大于1.29、信息维大于1.39的分区，中—大型铅锌矿床发育于容量维大于1.58、信息维大于1.42的分区。从分维值的地质意义及其与矿床发育规模、频数关系的角度来看，研究区内铅锌矿床分布的有利区应满足两个条件：首先分维值较高，容量维大于1.58、信息维大于1.42。其次存在相对阻挡—圈闭流体区的邻区。

（3）研究区铅锌矿床及金属资源量丛集性显著，资源量空间分布分维值为0.9313，矿床空间分布分维值为1.0096，划分出四级有利成矿区，其中Ⅰ级有利成矿区找矿潜力最大，在空间上呈NW向展布。

致谢感谢审稿专家和编辑部提出的指导与修改意见，对提高论文质量有很大的帮助，在此一并表示衷心感谢。