变形监测数据分析与预测方法探讨——以德州市某综合楼为例

王永峰

（德州市城乡规划编制研究中心，山东 德州 253000）

1 引言

随着建筑业的蓬勃发展，我国的高层建筑物越来越多，为了确保建(构)筑物的安全，避免造成经济损失和人身伤害，需要持续对建筑物进行变形监测，再利用合理的方法对监测获得的数据进行处理分析，对变形趋势做出准确预测，以便及时发现安全隐患并采取相应的措施，确保建筑物的安全。

建筑物变形受诸多外界因素的影响，各种因素之间关系错综复杂，变形预测的准确性对建筑物安全评估起着重要作用[1]，因此数据分析与预测方法的选取显得至关重要。本文结合德州市某综合楼工程，以其在建设过程中和运营后的变形监测成果为依据，重点对灰色模型和时间序列两种预测方法进行了相关探讨，介绍了两种方法各自的特点、适用条件以及建模预测的方法，旨在为保障建筑物的安全提供相关变形监测理论和技术支撑。

2 工程实例

2.1 工程概况

某综合楼位于德州市德城区，建筑面积为32118平方米，用途类型为商住，主体层数为22 层。通过对该建筑的主体结构进行变形监测及预测，及时发现异常并对危险源提前预警，确保建筑物的安全。依据规范和设计要求一共布设了3 个基准点和lO 个观测点，为保证测量成果的可靠性，使用精密几何水准测量的方法，并按照二等精密水准测量技术的要求，采用电子水准仪配一对2m 条码尺，固定人员、固定路线进行观测。沉降观测频率为：施工到±0 进行第1 次观测，第2 层开始到22 层每施工1 层观测一次，封顶后至竣工期间观测4 次，竣工后第一年每两个月观测一次，第二年每季度观测一次，直到达到稳定值(0.01mm／d)。1#-10#监测点前40 期的监测数据见表1。

表1 1#-10#监测点1-40期监测数据统计

2.2 数据分析与预测

（1）灰色模型数据分析与预测方法

灰色系统理论使用离散数据序列，建立动态模型，是研究复杂系统强有力的数学工具[2]。灰色系统理论是一种“贫数据”建模的方法，它通过对原始数据的处理和灰色模型的建立，作出科学定量的预测。它适合处理贫信息系统，能在贫信息条件下建立模型并进行预测。灰色模型建模思想虽然简单，但需要进行大量复杂的矩阵运算，通过建立加权灰色数列预测模型PGM（1，1）和评价指标来进行预测，它是单序列的一阶线性动态模型[3]。应用灰色模型进行预测具有的优点：样本数据少、原理简单、计算方便、短期的预测精度高和可检验等，因而它的应用广泛，也取得了较好的效果。将每期监测的数据进行平差处理后，经过计算得到监测点的累积沉降量，本次试验选取其中的l#和9#两个监测点进行分析，在沉降监测的整个过程中，部分观测点被遮挡，无法进行监测，因而缺失了部分数据，故以时间间隔为7 对原始数据进行等间隔插值处理。以l#和9#沉降监测点为例，选取30 期左右的原始数据分别建立GM（1，1）模型，预测后7 期的沉降量，具体步骤为：

从表2 可以看出，1#监测点的最大残差为0.0787，最小残差为0.0019，9#监测点的最大残差为0.1169，最小残差为0.0132。将1#和9#监测点的预测结果与原始数据进行对比，可见灰色模型预测的结果与实测数据基本吻合。因此，应用灰色模型对高层建筑的变形预测是可行的。

表2 灰色模型的预测结果

（2）时间序列法数据分析与预测方法

时间序列分析也叫动态数列分析，它是20 世纪20 年代提出的一种动态数据处理方法。时间序列预测法是将预测目标的历史数据按时间的顺序排列成为时间序列，然后分析它随时间变化的发展趋势，来推预测目标的未来值。时间序列预测法主要用于分析影响事物的主要因素比较困难或相关变量资料难以得到的情况，预测时先要进行时间序列的模式分析。

分解分析是时间序列分析和预测过程中常用的统计方法[4]，假设时间序列是随机波动、长期因素、周期变动、循环波动等因素综合影响的结果，分解过程首先从原始序列中消除随机波动，在此基础上，分别识别出其它要素的变化模式，解决随机波动则需要使用移动平均法来实现，操作简单且精确。

式（12）中，mt+1是t+1 期的预测值，其值为近期监测数据的平均值，n 为监测的期数。可以看出，移动平均法就是对近期的已有数据不断取平均值，随着时间的推移，新的数据不断引进，旧的数据被去除，“平均”起到了“滤波”的作用。

如果对一次移动平均值序列再进行一次移动平均，就得到二次移动平均值。用二次移动平均值进行预测的方法，就是二次移动平均法。二次移动平均法的计算公式为：

式中，n 为每次移动平均包含的数据个数，即期数；Mt+1为n 个近期数据的平均值，作为t+1 期的预测值。

②识别出长期因素、周期因素和循环波动的变化模式

长期因素=Yt/Mt，得到一组接近于1 的数列；对其取n 项平均（本文以取n=2）平均值，得到影响数据稳定的周期因素；最后用公式Dt=Yt/St，剔除循环波动因素，得到最终循环周期波动趋势Dt。

③计算预测值和残差ε

建立公式Dt=a×t+b，用计算出的Dt和监测周期t分别求出b 和a 的值，继而计算出预测值和其与样本值的残差ε。

确定了模型后，分别对点1#、9#观测点的沉降变化趋势进行预测，预测结果见表3，从表3 中我们可以得出，1#观测点预测的最大残差为0.0769，最小残差为0.0093；9#观测点预测的最大残差为0.0985，最小残差为0.0001。分别将1#和9#观测点的预测结果与实际观测数据进行对比，可以看出，总体上时间序列模型预测的结果与实测数据较吻合。因此，应用时间序列分析模型对高层建筑的沉降值进行预测也是可行的。

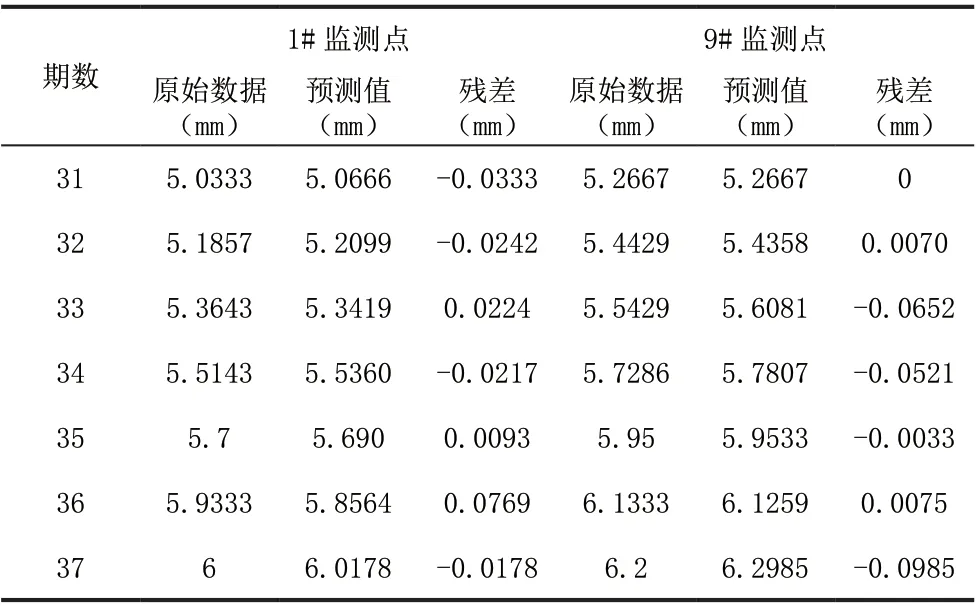
表3 时间序列分析预测结果

2.3 两种预测方法的比较

将两种预测方法进行比较，从对比分析的结果总结得出：

（1）灰色系统预测理论克服了传统数理统计方法的不足，在小样本且无特征分布的情况下，对建筑物变形的发展及特性进行了很好的预测和研究[6]，而且，灰色系统预测的精度较高，但是其残差却反映出误差明显增大的趋势，如果要解决这个问题，必须实时加入新的数据，即构成动态灰色模型。

（2）时间序列法对动态数据具有外延特性，当有新数据加入时不需要重新建立模型，数据的连续性强，对变形数据的随机波动性有较强的处理能力和适应能力[7]，时间序列法预测的精度显然更加均匀，残差在±0.5mm 上下波动，但是有的却接近±1.00mm，长期预测效果更佳。

（3）在进行长期预测时，这两种模型的效果都比较理想，预测的精度都比较高，两种方法均具有良好的应用价值。

3 结束语

变形观测是一个复杂的课题，面对一个庞大的建筑结构体以及不断变化的外界条件，单一的分析和预测方法往往具有片面性，难以全面地反映出变形体的变形规律[8]。

因此，在实际应用过程中，诸多学者将不同的预测方法以科学合理的方式进行组合，综合利用不同预测方法提供的多方面的信息，尽可能地提高预测的精度，以期合理、可靠、顺利地完成监测任务。