干扰条件下的雷达组网包络三维融合方法
蒋志强,刘思成
(四川大学计算机学院,成都 610065)
0 引言
电磁信息可视化是虚拟战场环境中不可或缺的重要组成部分,其中雷达信息的可视化尤其是雷达探测范围的可视化更为重要。雷达探测范围可视化不仅能够全面展示雷达电子战系统的作战态势、进程和对抗结果,还有助于指挥员对战场电磁态势进行准确判断、科学决策、合理部署和调配战场电子对抗力量,但是,多个雷达探测范围形成的包络会在空间中重合,不仅带来了信息冗余的问题,也不利于雷达网态势的统一,因此,需要借助一种方法,使得雷达网中的多个雷达包络具有统一的融合态势。
文献[3]提出一种基于多边形布尔运算原理的二维雷达包络融合算法,该算法主要利用雷达包络的几何性质来对包络重合区域进行融合。文献[4]针对二维多雷达包络数据可视化后数据丢失的问题,提出一种可以对多雷达包络线进行提取的雷达包络检测算法,同时,还采用位图技术对包络线进行快速绘制。以上研究都是针对二维平面下雷达网中的多个包络进行融合的情况,与三维空间中的包络融合情况不同。在三维电磁态势可视化中,雷达包络是对雷达探测范围模型计算的结果采样来进行绘制的,对雷达网中的包络数据进行融合需要对每一个采样点进行包络内外判断。由于三维空间中的雷达包络形态相较于二维雷达包络更为复杂,无法简单直接地判断采样点与包络的关系,同时,采样点的数量也直接影响着融合算法的时间复杂度,因此,对三维空间中的多雷达包络融合算法研究具有重要意义。
文献[5]在三维雷达包络通用建模的基础上,通过三角形对的快速相交检测算法完成三维雷达网包络融合。文献[6]对三维雷达网中的多个雷达包络组进行垂直投影和水平投影,然后通过过滤投影后的数据点,筛选出重叠区域的雷达探测点来实现融合。文献[7]则是通过将BSP 树与三维几何体布尔运算相结合的方式解决雷达包络融合问题。以上算法虽然完成了对三维雷达网的包络融合,但是针对多干扰机干扰条件下的雷达网包络模型不具有有效性,同时,在实时系统环境下使用也存在一定局限性。
在已有多干扰机干扰条件下雷达探测模型的基础上,本文提出一种雷达组网包络的三维融合算法。首先,该算法在规定的方位角和俯仰角范围内以特定采样间隔对干扰下雷达探测模型计算,并对结果进行采样,得到雷达网包络的数据采样点集合;然后,针对每一对雷达包络数据采样点集进行融合区域判断,过滤掉大部分的非融合区域数据点;最后,通过对融合区域内的数据采样点进行包络的内外判断完成对雷达网包络数据的三维融合。该算法通过利用雷达包络水平投影后的图形的几何性质判断两个雷达包络的融合区域,同时,还通过判断数据采样点的消隐属性来减少融合算法对采样点的重复处理,使用上述两种策略可以降低时间复杂度,以保障算法的实时性和有效性。
1 雷达包络数据生成
雷达态势的三维可视化一直以来都是许多学者研究的重点内容,其中,雷达探测范围的可视化从二维的表现方式逐渐扩展至三维。文献[1]在综合考虑了大气吸收衰减和地形影响的情况下,结合分步傅立叶解抛物方程的方法计算出雷达的最大探测范围;文献[8]根据光的直线传播原理,分析了雷达探测范围在地形影响下的变化情况,同时,还结合干扰方程实现了在多干扰源条件下的雷达三维包络;文献[9]在雷达方程的基础上,建立了基于雷达、探测目标以及干扰机的空间位置信息的雷达探测范围三维模型,并以较为真实的方式展现了干扰机在不同方位对雷达探测区域的影响。在战场环境下,雷达的探测范围会受到诸如雷达功率、雷达天线增益、雷达压制系数、干扰机功率、干扰机极化损失等设备自身性能的影响,同时探测目标的反射截面积、大气环境、地形等外界因素也会对雷达的探测范围造成影响。
本文采用式(1)计算在多干扰机干扰条件下雷达的探测范围:


通过上述计算模型计算出干扰条件下雷达的探测范围后,还需要对包络数据的采样过程以及采样结果的数据结构进行规范,以便后续的融合区域判定和融合算法对数据集合的处理。针对雷达最大探测边界的采样示意图如图1所示。
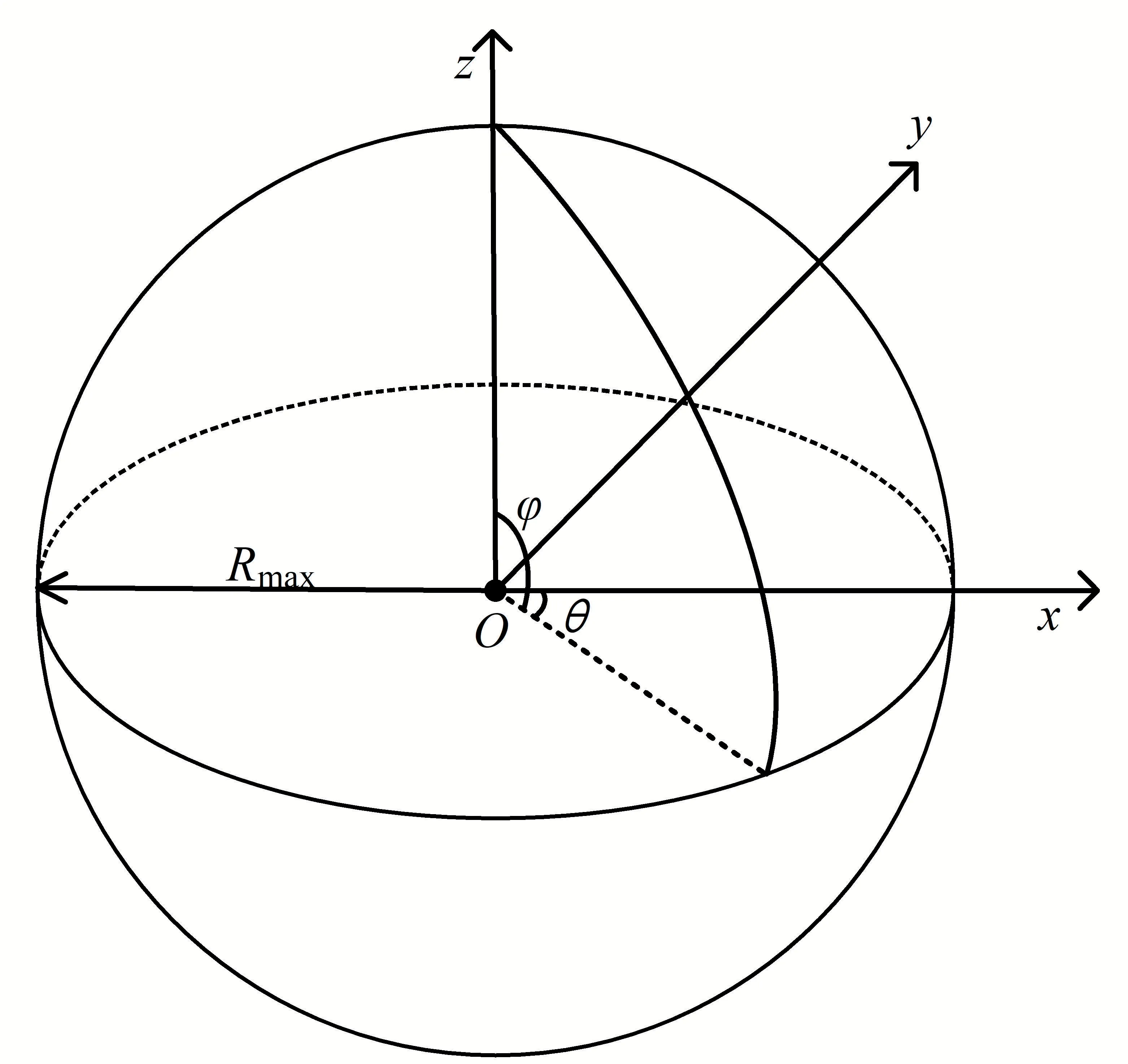
图1 雷达包络数据采样示意图
以雷达所在位置为坐标原点,正东方向为x 轴正向,正北方向为轴正向,由地心指向地表的方向为轴正向,设俯仰角为,采样间隔为Δ,采样范围为0 °~90 °;方位角为,采样间隔为Δ,采样范围为0°~360°,依次以逆时针方向对边界数据进行采样,采样流程如图2所示。

图2 雷达包络数据采样流程图
单个雷达采样结果数据集合的数据结构如表1 所示,除最后三个数据外(其中第-2 行存放的是由融合区域判定算法计算得到的起始方位角θ和终止方位角θ信息,标志位1 为true 表示融合区间为[ ]θ,θ,为false 表示融合区间为[ 0°,θ]∪[θ,360° ];第-1 行存放雷达位置信息;第行存放雷达编号、雷达最大探测半径以及标志位2,其中,标志位2 为true 时表示该雷达包络已经计算过融合区间,反之则表示未计算过融合区间),其余数据均为对雷达最大探测边界进行采样后的位置信息。

表1 单个雷达采样结果数据集的数据结构
2 融合区域判定
完成对雷达网中各个雷达包络数据的采样以及数据整理后,就可以对雷达包络数据进行融合处理。通过观察雷达组网中多个雷达包络的重合区域可以发现,并不是所有的雷达采样数据点都在重合区域内,位于非重合区域的包络数据是可以不用参与融合计算的。如果直接对原始数据进行融合处理,那么融合算法的高效性就无法得到保障。因此,在进行融合算法流程之前,需要对雷达网中的融合区域进行判定,以便过滤掉不需要进行融合处理的雷达采样数据点,在一定程度上降低融合算法对数据的处理时间,提高融合算法的效率。
在受到干扰机干扰的条件下,两部雷达的探测范围在水平面上的投影结果如图3所示。

图3 融合区域判定示意图
其中阴影部分为两部雷达探测范围的实际重合区域,而由弧型虚线包围的区域为两部雷达最大探测半径所组成的圆的相交部分。为了找到融合区域,就需要确定两个雷达包络各自的方位角范围,在这个方位角范围内的雷达探测点都是需要被融合处理的。但是,由于干扰条件下的雷达包络形状并不规则,如果利用其几何性质或干扰方程直接求解交点,势必会增加融合区域算法计算量和复杂程度。同时,考虑到雷达包络数据会因为干扰机的位置变化而做出相应变化的情况,融合区域算法的实时性也难以得到保证,因此需要一种时间复杂度更低的融合区域判定算法来筛选出重合区域中的雷达探测点。观察图3可以发现,雷达探测范围的实际重合区域在虚线内部,而虚线所组成的区域范围表示的是两部雷达的最大探测半径所构成的圆的相交部分,因此,可利用圆的几何性质求得两圆交点,进而求得雷达包络采样方位角范围,得到融合区域。为缩小雷达网融合区域的搜索范围以及降低融合区域判断算法的时间复杂度,本文依次选取雷达网中不同的两个包络作为一组进行融合区域判定算法的数据,具体流程如下:
(1)设被选取的两部雷达的位置分别为(,)、(,),最大探测半径分别为、,若、两点距离大于或等于与之和,或者、两点重合,则选取的两部雷达包络没有重合区域,不需要进行融合处理,转到(5),否则,转到(2);
(2)由式(2)并结合圆的几何性质可以求得两部雷达最大探测半径所组成的圆的交点分别为(,)、(,),其中>,转到(3);

(3)由式(3)分别求得、点相对于点的方位角(其中x与y表示点与点的轴分量和轴分量,x与y表示点或点对应轴分量,点(x,y)为( 1,0 ),表示轴为正的方向),并记为、、、,转到(4);

(4)若<,当值小于0时,雷达A的融合区域方位角范围为[ 0°,]∪[,360° ],雷达B 的融合区域方位角范围为[,];当值大于或等于0时,雷达A的融合区域方位角范围为[,],雷达B 的融合区域方位角范围仍为[,];若>,则将上述情况中的雷达A 和雷达B 进行互换即可。转至(5);
(5)从雷达网中选取两个不同且存在未进行过融合区域判定的雷达包络重复以上步骤,直至雷达网中的所有包络都进行过融合区域判定。
3 融合算法
确定雷达网中的两个雷达包络的融合区域之后,就需要对区域内的采样数据点进行融合处理,对位于雷达包络内部的采样点进行过滤,考虑到采样点数据是单个雷达探测性能的一种描述信息,不能直接将其删除。因此,本文采用消隐的方式,即设置采样点的颜色透明度属性值为0 来进行过滤。整个融合算法流程如图4所示。

图4 融合算法流程图
整个融合算法流程如图4所示,首先从雷达网包络中选择两个具有重合区域的雷达包络数据并对这两个雷达包络数据进行融合区域判定,即计算出两个雷达包络的融合区间;然后,针对融合区间内的数据点进行内外判断以及融合处理;最后重复以上流程直至雷达网中的包络数据处理完毕并将融合处理后的雷达网包络进行输出显示。其中,对于融合区域内的数据点如何进行内外判定的计算流程如下:
(1)设为雷达A 在融合区域内的采样数据集合,V为雷达B的采样数据集合,Δstep为雷达B在方位角上的采样间隔,Δstep为雷达B 在俯仰角上的采样间隔,C( )x,y,z为雷达B的位置;
(2)设P( )x,y,z为中的任一颜色透明度不为0的采样数据点,按式(3)与式(4)计算出P相对于雷达B 位置的方位角θ以及俯仰角φ;

(3)由θ以及φ计算雷达B 中最邻近的采样方位角θ以及采样俯仰角φ,具体计算方式为:分别计算θ以及φ对Δstep以及Δstep取模的结果,记为R和R;若R≤Δstep2,则θ= θ- R,否 则θ= θ+(Δ step- R);若R≤Δstep2,则φ= φ- R,否则φ= φ+(Δ step- R);
(4)根据θ和φ从采样数据集合V中取得最邻近采样点P(,y,z),分别计算P与P相对于雷达B 的位置C的长度并记为L和L,若L≤L,则P位于雷达B 内部,并将点P的颜色透明度设置为0;反之,则位于外部,不进行处理。
对整个融合算法进行时间复杂度分析:对于融合区域判定算法,其主要流程是从雷达网中选择具有重合区域的雷达包络组,并从雷达包络中判定各个雷达的融合区域方位角范围,因此其时间复杂度为(+(- 1) + … + 1) ≈(()为雷达网中雷达包络的个数);对于采样数据点的融合算法,其主要流程是针对雷达A和雷达B 包络融合区域方位角范围内的采样数据点进行内外判断以及消隐处理,因此其时间复杂度为(+()和分别为雷达A 和雷达B融合区域内颜色透明度值不为0的采样数据点个数)。综上,整个融合算法的时间复杂度为(×(+)),其中,包络融合区域内的采样数据点个数是影响该算法时间复杂度的主要因素,但因为在进行采样数据点内外判断算法前,对不在重合区域内以及颜色透明值已经为0的数据点进行了过滤,所以在一定程度上减少了需要被处理的采样数据点个数,降低了整个融合算法的计算量。
4 仿真实验
本文根据式(1)生成三组干扰机干扰条件下的雷达包络数据,其中雷达的性能参数如表2所示,干扰机的性能参数如表3所示。

表2 雷达参数

表3 干扰机参数
以水平方向上的采样间隔5°与垂直方向上的采样间隔3°的条件对雷达包络数据进行采样,得到采样数据点集合。对以上数据点集合进行绘制得到的未经过融合处理的雷达包络如图5、图6所示,三个雷达包络组成的雷达网中存在着明显的重合区域,需要对重合区域内的采样数据点进行融合处理,融合后的雷达包络如图7、图8所示,本文提出的融合算法对重合区域内的采样数据点进行了有效的消隐处理,整个算法耗时8 ms,满足实时性要求。

图5 未融合的雷达组网包络俯视图

图6 未融合的雷达组网包络正视图

图7 融合后的雷达组网包络俯视图

图8 融合后的雷达组网包络正视图
本文分别分析了雷达网中的重合区域个数与数据采样间隔大小对CPU 计算时间的关系,如图9、图10 所示,在水平采样间隔与垂直采样间隔都为5°的情况下,重合区域的数量越多,CPU 计算时间越多,其中,重合区域数量为8时,CPU 计算时间为49 ms;在重合区域数量为3时,CPU 计算时间会随着采样间隔增大而逐渐缩短,其中,采样间隔为1°时,CPU 计算时间为98 ms。因此,处理重合区域数量小于8 且水平采样间隔与垂直采样间隔均大于1的干扰下的雷达包络三维融合问题时,本文提出的融合算法能够满足实时性和高效性的要求。
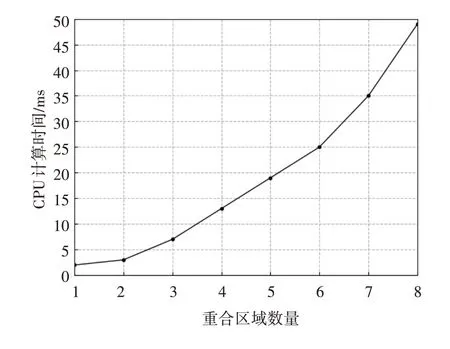
图9 重合区域数量与CPU计算时间的关系(采样间隔为5°)
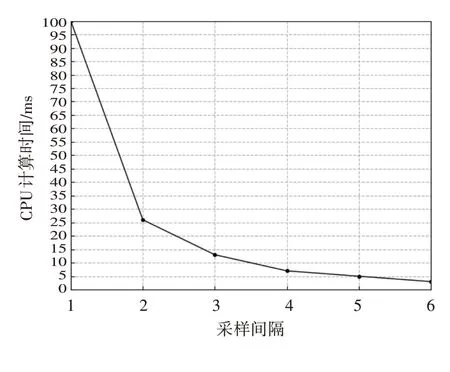
图10 重合区域数量为3时采样间隔与CPU计算时间的关系
5 结语
针对干扰条件下的雷达组网包络三维融合问题,提出了一种融合算法,该算法首先对采样后的雷达包络数据点集合进行重合区域判定,然后对重合区域内的采样数据点进行包络内外判断并将位于包络内部的点以消隐的方式进行处理,最后进行融合后的雷达网包络绘制,从仿真实验结果来看,该算法能够有效地对雷达网中的重合区域进行融合,消除冗余数据信息,让指挥员更加直观地观察到雷达网的探测范围。但是,由于该算法的主要流程是基于采样数据点的,采样过于密集或雷达网中的重合区域数量过多时,会导致融合算法的CPU 计算时间增加,降低算法性能,因此,如何优化算法,以使得算法能够在数据量过多的情况下仍然满足实时性和有效性的要求,将是后续需要研究的内容。

