改进粒子群算法求解车间作业调度问题
葛 晶,高广宇,王虔翔
(北京理工大学计算机学院,北京 100081)
0 引 言
(1)问题背景介绍
在企业生产当中存在着生产环节多、合作关系复杂以及生产的连续性强等特点,如果某一个生产的节点发生变化(例如某一台机器发生故障,工件的处理工序改变)会影响到整个生产系统的运行,一般来说,企业会安排一个专门的部门来管理生产调度,这无疑耗费大量的人力物力。车间作业调度问题是很多实际生产调度问题的简化模型,具有重大的理论价值和工程实践价值,是目前研究广泛的典型调度问题。
(2)问题数学描述
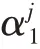
对于每个工件和每一个机器,令x作为在上的开始时间,目标函数为,问题可以表示为:
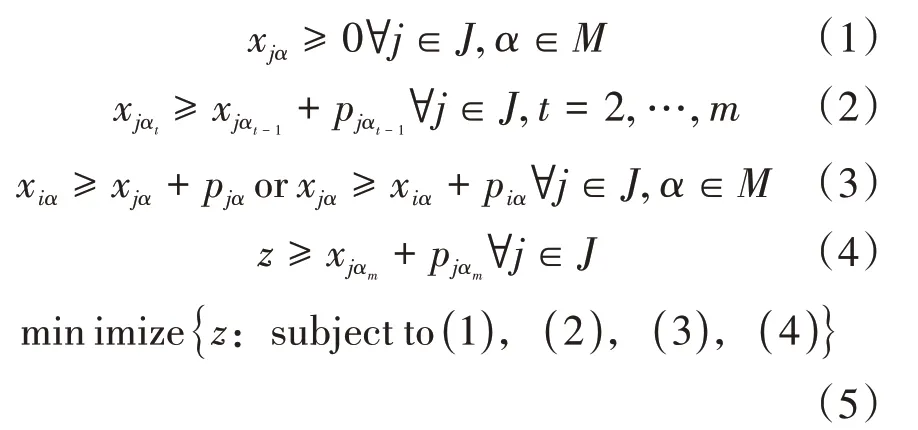
(3)解决方案及实验效果
本文采用改进的粒子群优化算法来解决车间作业调度问题,算法的关键步骤如下:①初始化粒子的速度和位置;②将位置信息编码为作业的调度顺序并计算总完工时间;③更新粒子的个体最优解和所有粒子全局最优解;④利用个体和群信息更新粒子速度,利用速度更新粒子的位置。但是,即便很小的位置变化也容易引起编码顺序的巨大改变,因此该算法局部搜索能力很差。
为了解决这一问题,本文提出的方法在每次迭代中,每个粒子的更新一定概率上使用传统粒子群位置、速度更新公式,同时以一定概率将其当前位置与其历史最优位置进行交叉来更新。同时,为了提高历史最优位置处的局部搜索能力,采用位置交换(变异)来代替传统位置更新,即原始算法用于全局搜索,交叉变异用于细化局部搜索。实验证明,本文提出的方法可以实现比标准PSO 更快更好的效果,同时可以在牺牲少量速度的前提下,进一步提升实验效果,在给定用例上取得了最优的测试结果。
本文后续部分组织如下。第1节详细陈述使用的方法,第2 节报告实验结果,第3 节讨论本文的方法并总结全文。
1 算法设计
1.1 算法简介
对于车间作业调度问题(job shop scheduling problem, JSSP),启发式算法可以在可接受的时间内得到近似的最优解。该算法主要包括两类:构造性启发式算法和元启发式算法。尽管构造性启发式算法可以在解空间中找到问题的解,但它依赖于问题的局部信息,得到的解一般是局部最优解;元启发式算法是一种优化算法,它的灵感来自于自然原理,并以公式化的方式描述了自然界中的一些问题。元启发式算法能在可接受的时间内得到最优或近似最优解,已成为解决各种调度问题的一种实用可行的算法。
元启发式算法主要包括克隆选择算法(clonal selection algorithm,CSA),模拟退火算法(simulated annealing,SA),遗传算法(genetic algorithms, GA),基于生物地理学的优化算法(biogeography-based optimization, BBO),粒子群优化算法(particle swarm optimization,PSO),差分进化算法(differential evolution,DE),蚁群优化算法(ant clony optimization,ACO),等等。为了获得良好的性能,元启发式算法需要找到一些策略来平衡算法的局部搜索能力(利用)和全局搜索能力(探索)。元启发式算法的优势在于,它可以在理论上将两者以最优方式结合起来。
Qiu 等将人工免疫系统(artificial immune system, AIS)理论和PSO 结合起来解决车间作业调度问题JSSP,该算法采用克隆选择和免疫网理论来模拟免疫、克隆、超突变、抗体选择等基本过程。Masood 等提出了一种混合的遗传算法来解决多目标的JSSP。Zhang等提出了一种基于克隆选择理论的新PSO,以避免过早收敛。Abdel-Kade在PSO 中引入了两个基于邻域的算子以解决JSSP 群体多样性。Dao 等提出了一种具有混合通信策略的并行蝙蝠算法(bat algorithm, BA)来解决JSSP,该算法的每个子群通过通信策略相互联系,并分担处理器上的计算负荷,该算法有很好的准确性和收敛率。
与其他元启发式群体智能算法类似,PSO是一种创新的全局优化算法,最早由Kennedy博士和Eber 博士提出。PSO 思想来源于鸟群的觅食行为,即每个粒子代表鸟群中的鸟,在搜索空间中进行单独搜索,获得的个体最优值作为个体极值,并将个体极值与其他粒子的个体极值进行信息共享。粒子群中所有粒子的最佳个体极值作为当前的全局最优解,每个粒子根据自身的个体极值和当前的全局最优解更新自己的速度和位置,通过不断地更新迭代获取更好的全局最优解。PSO 粒子群算法因为参数少,收敛速度快,已经成为一种非常成功的算法,并已被用于优化各种实际问题。同时,开发和探索对应算法的局部优化能力和全局优化能力,虽然PSO 算法有很强的开发能力,但其探索能力是非常差的。当初始解离全局最优解较远时,PSO经常出现过早收敛和局部停滞。
考虑到越来越多的混合元启发式算法被用于解决JSSP,并且从平衡算法的全局搜索能力和局部搜索能力的角度来分析算法的性能。因此,为了克服PSO 的上述缺点,有必要引入一些策略来有效地平衡开发和探索。针对车间作业调度问题,本文设计了编码方案,同时添加了交叉变异的局部搜索功能。
1.2 算法关键操作
1.2.1 编码和解码
对于个工件,个机器的车间作业调度问题,粒子的维度为×,每个粒子位置代表一种处理顺序。
编码:首先每个粒子根据位置进行升序排序,然后进行分组,每个为一组,规定最小的一组为工件1,第二组为工件2,以此类推,第组为工件。将位置从连续的实数更改为工件号后还原回原来的粒子位置顺序,这时每个粒子的位置就代表工件的调度顺序。
解码:每个工件的第一次出现代表该工件的第一道工序,第二次出现代表该工件的第二道工序,以此类推,我们可以得到完整的调度顺序。
1.2.2 粒子状态更新
对于每个粒子,更新的类型是概率确定的,q的概率执行标准速度、位置更新,其中∈[ -,],∈[ -,],公式如下:

1 - q的概率执行交叉变异,当前位置与其个体历史最优位置进行交叉,由于部分交叉产生的变异依然是巨大的,不利于局部的搜索,因此这里选择完全交叉,即将粒子位置重置为其历史最优位置,同时随机交换两个位置的坐标来产生变异,更新公式如下:

1.2.3 全局最优位置的额外的变异搜索
为了进一步提高局部搜索能力,针对全局最优位置进行额外的变异搜索,借鉴常桂娟提出的局部搜索方法,对全局最优位置随机交换两个位置的坐标。如果得到更优结果则更新最优位置,否则保留原全局最优位置。在这里本文添加探索次数为s,即执行s次上述操作以寻找更优。由于这种方法得到新的最优位置不属于任何一个粒子的历史最优,无法利用本文提出的粒子的交叉变异进行更新,因此默认将第一个粒子的历史最优位置更新为目前新得到最优位置。
1.2.4 自适应的惯性权重
当粒子的所有速度都等于最大速度时,粒子很难达到最优位置,因此引入惯性权重,大的值有利于粒子群的探索,小的值有利于局部的挖掘,由于本文提出的方法需要同时兼顾全局与局部搜索,因此我们设计动态变化的惯性权重来应对不同的情况,这里采用Nikabadi等提出的一种自适应的惯性权重方法,每个粒子基于它离局部最佳位置的距离得到自己的惯性权重,公式如下:

基于上述分析和描述,所述算法的基本流程如图1所示。
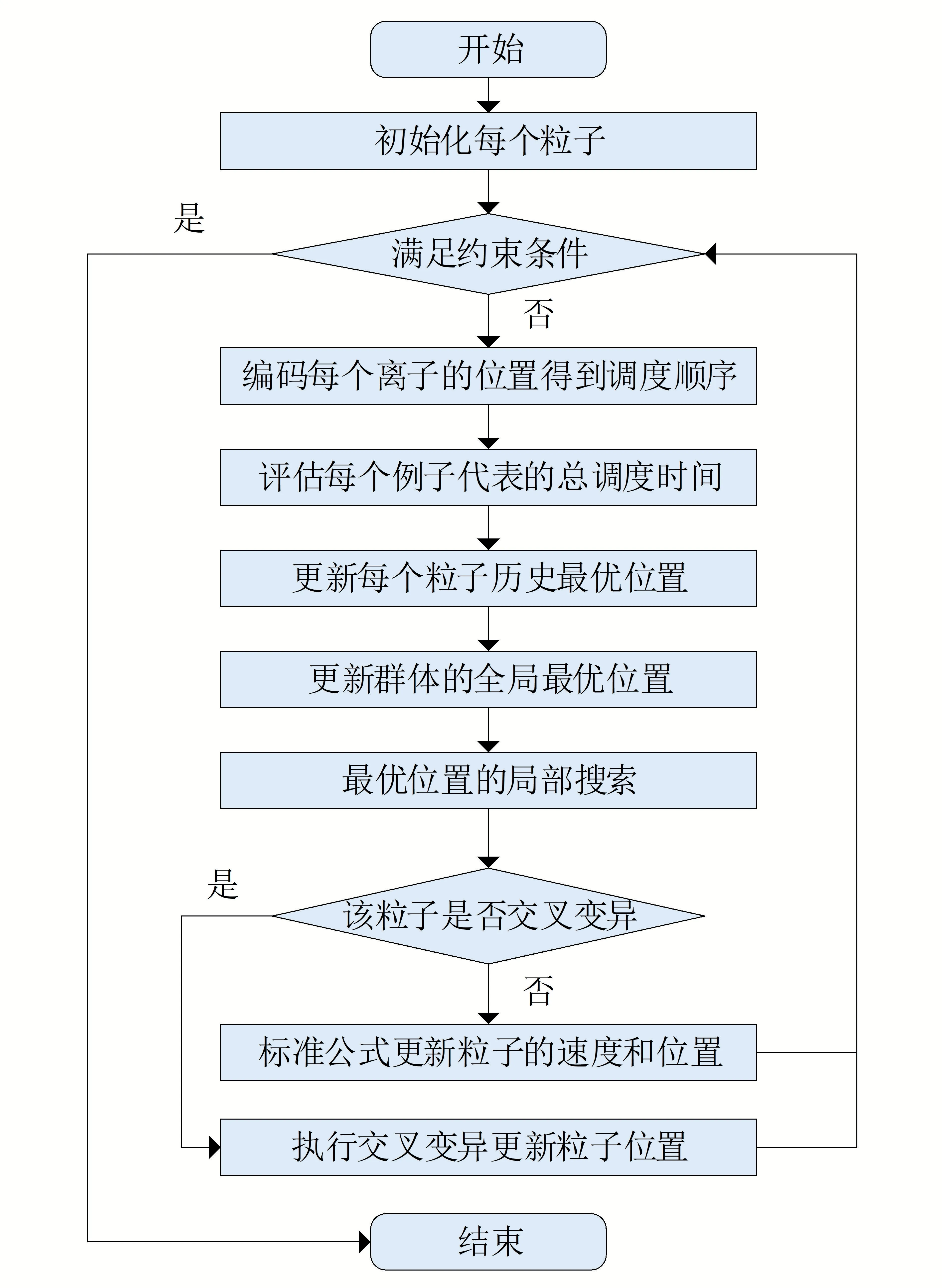
图1 算法流程示意图
1.3 时间复杂度分析
给定算法的粒子个数为,每个粒子的维度为。
(1)用标准公式更新所有粒子的速度和位置。对每个粒子调用速度和位置更新公式,时间复杂度为(×)。
(2)编码所有粒子的位置。排序默认使用快排,时间复杂度为(×log)。
(3)计算每个粒子总调度时间。定义两个列表,一个列表记录每个工件的累计加工时间,一个列表记录每台机器上的累计加工时间,只需要扫一遍粒子的编码便可以更新两个列表。最终机器上累计加工时间最长的为总调度时间,因此时间复杂度为(×)。
(4)更新所有粒子的惯性权重。每个粒子根据历史最优值更新其惯性权重,因此时间复杂度为()。
(5)交叉变异。需要扫一遍每个粒子的历史最优位置,因此时间复杂度为(×)。
2 实验及分析
2.1 实验设置
(1)实验环境:Windows10 系统、JetBrains PyCharm软件、Python3.6语言
(2)最大运行时间:未设置
(3)实验参数:
迭代次数设置为2000,粒子数40 个,设置为1,位置初始化∈[ -,],设置为0.25,速度初始化为0。参数,都设置为0.5,( 0 )设置为0.9,(n)设置为0.4,执行标准更新的概率q初始值设为0.95。采用线性递减的方式,在迭代1000 轮时递减为0.05,即训练的前期重点利用标准PSO 进行全局的搜索,后期重点利用交叉变异进行局部的搜索。全局最优的进一步探索次数s设置为10,该参数越大效果越好,同时用时也越长。
2.2 实验结果
2.2.1 测试用例实验结果及分析
算法执行均采用上述提到的参数,每个测试用例运行10 次,以找到的最优解作为用例的运行结果,同时输出10 次运行的平均时间,作为该测试用例的运行时间。
实验结果如表1 所示,由于用例0 的正确答案是已知的1234,从运行结果来看最小结果1251 已经很接近正确答案,说明了本文提出算法的有效性,同时平均结果1274 与最小结果相差不大,说明了算法的稳定性。

表1 运行结果与运行时间
从结果来看,对于小规模用例,例如用例3,最小结果和平均结果一样,说明算法对于小规模用例具有较高的精准度和稳定性。对于大规模用例,例如用例8 和9,依然具有较好的稳定性。
从运行时间来看,最小的用例只需要16.9 s,最大的用例需要228.9 s,并不需要太多的时间便能得到较好的效果。但是单独观察该实验结果很难得出更多有用的信息,因此接下来与标准PSO进行对比试验,来说明算法的有效性。
2.2.2 对比试验
首先进行本文所提出的改进粒子群算法与标准粒子群算法的对比试验,标准粒子群算法使用的参数与实验设置一致,以保证对比的真实性,同样每个用例运行十次,运行时间取平均值。
如表2所示,改进的PSO算法无论是最小结果还是平均结果都明显优于标准的PSO 算法。测试用例规模越大,其优势也越明显,改进PSO 算法保留了标准PSO 算法收敛速度快的优点。同时对于局部探索的改进弥补了PSO 局部搜索能力差、精度低、易发散的问题。

表2 标准PSO与改进PSO结果对比
从运行时间来看,改进PSO 算法用时比标准PSO 略大。从算法角度来讲,如果只添加交叉变异的思想用时会更少,因为粒子交叉操作重置位置为历史最优时间复杂度为(),变异操作随机交换两个位置,时间复杂度可以忽略不计。而标准PSO 速度和位置更新时间复杂度都是(),一共是(2)。那么改进PSO 算法多出来的时间消耗必然是由于全局最优位置的局部探索导致的。因为设置每次探索次数为10,虽然10 次随机交换并不耗时,但是每次交换需要进行编码求解,调度是很耗时的。为了验证在相同的用时情况下改进PSO 能否取得更好的效果,我们将探索次数置为1,再一次进行对比。
如表3所示,只添加交叉变异操作不执行全局最优位置的局部探索,运行时间的确比标准PSO 的运行时间还少。同时算法的运行结果依旧在很大程度上优于标准PSO。也就是说,本文提出的算法不仅提高了PSO 的搜索速度,同时极大地改善了PSO的搜索精度。

表3 标准PSO与改进PSO(无全局最优的局部探索)结果对比
3 结语
本文提出了一种增强局部搜索能力的粒子群优化算法用于求解车间作业调度问题,算法保留了标准粒子群算法良好的全局搜索能力,同时解决了其局部搜索能力差的问题。改进算法局部搜索能力的增强主要体现在对于每个粒子按概率重置到其历史最优位置,并进行进一步的变异搜索。同时,对于全局最优位置进行额外的变异探索,如果是好的变异便保留。除此之外,为了使粒子更好地进行探索,采用自适应的惯性权重使得粒子在全局搜索时惯性权重更大,局部搜索时惯性权重更小。实验证明本文提出的方法可以实现更快的搜索速度和更高的精度,同时可以在牺牲少量速度的前提下,进一步提升实验效果。本文方法也存在一定不足,例如,算法在一定程度上依赖标准粒子群优化算法的全局搜索能力,未来还可以进行诸多改进尝试。例如,实验证明全局最优位置的额外探索取得了很好的效果,那么次优位置应该也有很大的价值,设计更加精细的局部探索框架也能提高算法搜索最优解的能力。

