Cross-focusing of two chirped Gaussian laser beams and THz wave generation in plasmas of multi-ion species under a weakly relativistic and ponderomotive regime

M R JAFARI MILANI,S REZAEI and M J JAFARI

1 Photonics and Quantum Technologies Research School,Nuclear Science and Technology Research Institute,Tehran 14665-678,Iran

2 Plasma and Fusion Research School,Nuclear Science and Technology Research Institute,Tehran 14399-51113,Iran

Abstract The generation of terahertz(THz)waves via the beating of two high-intensity chirped Gaussian lasers in a multi-ion-species plasma is numerically studied by taking into account the weak relativistic and ponderomotive regime of interaction.The coupled differential equations for beamwidth parameters are extracted by introducing the dielectric function of such plasma and using WKB and paraxial ray approximations.The amplitude of THz radiation at beat frequency resulting from the nonlinear current density induced by the beat ponderomotive force of the cross-focusing of beams was obtained.The impacts of the chirp frequency parameter,initial laser intensity and initial ionic species density(specifically,the presence of singly and doubly charged ions) in the plasma on THz generation were discussed.Our numerical results reveal that THz radiation generation strongly depends on the chirp frequency parameter.A specific range of chirp frequencies exists for self-focusing as well as THz generation with a‘turning point’,where the THz emission reaches its maximum value.The results show that the strength of self-focusing and consequently the generated THz radiation are reduced by increasing the density of doubly charged ionic species in the plasma due to the suppression of the nonlinear effects.

Keywords: laser-plasma interaction,THz generation,chirped Gaussian laser beams

1.Introduction

In the progress and development of the technology of ultrashort high-intensity laser pulse generation,numerous phenomena have been observed during the interaction of lasers with plasma and gas targets [1-5].Various instabilities and nonlinear phenomena such as stimulated Raman scattering,filamentation [1],self-focusing [2-4]and high harmonic generation[6,7]are likely to arise with the propagation of an intense laser pulse in a plasma.Solid-state materials,such as gallium arsenide,lithium niobate and lithium tantalite,are widely used in terahertz (THz) generation [8].The main problem in nonlinear crystals is the damage threshold,which limits the higher level of initial pump laser intensity and as a consequence THz generation.Among these,THz emission based on plasma has attracted researchers’ attention as it prevails over the damage threshold limitation of conventional THz resources [9,10].Research to achieve strong THz radiation as well as high conversion efficiency has a particular importance because of its wide applications in material identification [11,12],biomedical imaging [13],nondestructive testing of materials such as polymer,ceramics and composites [14],time domain spectroscopy [15]and timeresolved THz microscopy [16]and communication technology[17].Therefore,many attempts have been made to relate THz generation to the nonlinear laser-plasma interactions[18-21].The generation of THz radiation from laser-induced filaments has been studied by means of numerical methods[22-30].Recently,in a theoretical study carried out by Kumar et al [31],a significant enhancement in THz amplitude was reported due to the self-focusing of an amplitude-modulated Gaussian laser pulse propagated in a rippled plasma.Numerous studies have shown that laser characteristics as well as plasma properties play a crucial role in the evolution of laser beams propagating in the plasma and THz generation.Among these properties are the presence of ions with a higher ionization degree in the plasma and the chirp frequency of laser beams.Regarding this,Neyra et al [32]studied the effect of a chirped pulse on the spectral characteristics of high harmonic generation in the classic as well as quantum approaches.They realized that the chirp parameter has a strong effect on the behavior of the maximum cut-off extension.Moreover,Wani et al [33]showed that employing a chirped pulse can minimize the beam defocusing caused by linear absorption and promote the self-focusing mechanism in a collisional plasma.Also,the influences of the laser intensity,plasma density and decentered parameter on the self-focusing of the Hermite-cosine-Gaussian chirped pulse in a collisionless cold plasma have been extensively analyzed by Thakur et al[34].Their results exhibit strong and earlier self-focusing of the incident chirped pulse in the presence of an exponential density ramp.More recently,the study of Mehta et al [29]revealed that applying an external magnetic field along with frequency chirping of the pump laser has a positive effect on the THz generation;in fact,the magnetic field performs a significant role in keeping the resonance conditions.Further,in order to get close to the real conditions of plasma,Misra et al [35]took into account a multi-ionized plasma with two different species and investigated the self-focusing using an analytical model.The effects of the space-charge field due to the density change of ionic species and also the charge composition on the beam dynamics of lasers and subsequently THz treatment in a multi-ionized plasma were also studied in an another work by Jafari et al [27].So far,different aspects of the initial parameters’ effect on THz yield have been investigated;however,there still exist unknowns relevant to plasma-based THz wave generation,which should be thoroughly analyzed for experimental applications.Mostly the laser-produced plasmas encompass multiple ion species.But due to software limitations and mathematical convenience,most past studies have considered the interaction between lasers and plasmas with only one charged ion and electron,while doubly,etc charged ions are neglected.In this work,in describing the THz generation in the plasma using the cross-focusing of two chirped Gaussian laser beams,we have taken into account the presence of multiply charged ions simultaneously.For this purpose,in the present work,the effects of frequency chirp on the cross-focusing of two Gaussian laser beams and also THz radiation generated in a weakly relativistic plasma consisting of multi-ion species,have been semi-analytically studied.The impacts of the chirp parameter,the ratio of densities of different ion species and the initial laser intensity on the THz generated in the plasma are investigated.First,from the wave equation and in the paraxial approximation,we derived a nonlinear differential equation governing the beamwidth parameterfof the pump lasers as a function of the distance of propagation.Then,the modified electron density distribution (and consequently the dielectric function of the plasma) is extracted by taking into account the relativistic ponderomotive force associated with the laser beams,space-charge field and the neutrality condition.Finally,radiated THz amplitude due to the two laser beams beating is introduced.The paper is organized as follows.Theoretical considerations for the filamentation of two Gaussian laser beams and THz generated wave equations are given in section 2.The results are analyzed and discussed in section 3,and section 4 summarizes our conclusions.

2.Theoretical considerations

2.1.Cross-focusing of chirped Gaussian laser beams

Considering the propagation of two linearly polarized Gaussian laser beams in a plasma (containing two or more ionic species) along the z-direction,the electric field vector for the laser beams is

whereAq(r,z)=A0q(r,z) exp (−ikq Sq(r,z))is the complex amplitude of the Gaussian beam,Sqis called an eikonal function,qωis the frequency of the laser beam,ω1=ω0(1+bω0(t−z/c)),whereω0is the incident laser beam frequency with no chirp andbis the chirp parameter.The frequencyω2is chosen as the difference,ω1−ω2=ωT,which lies in the THz domain.The propagation of laser beams in an underdense plasma can be described by a wave equation is the wave number of the beam,cis the speed of light in the vacuum andε0qreturns to the dielectric function in accordance with the maximum electric field over the axis(i.e.r=0)[36].We can assume that the frequency of the laser beam is positively chirped and given as as follows:

In the case of a Gaussian laser beam,A0qcan be expressed by

whereA00andf(z) are the initial electric fields’ amplitude and the dimensionless spot size parameter of the beam,respectively.In the paraxial ray approximation(i.e.r/r0≪1),the eikonalScan be expanded as

Substituting equations (1),(3) and (4) in the wave equation and following the approaches proposed by Akhmanove et al [37]and Sodha et al [36]by adoptingWKB(neglecting the term∂2A/∂z2when assumingA(r,z)to be a slowly varying function ofz) and paraxial approximations,separating the real and imaginary parts and collecting the coefficients ofr2on both sides,the set of differential equations conducting the dimensionless beamwidth parametersfqcan be depicted as

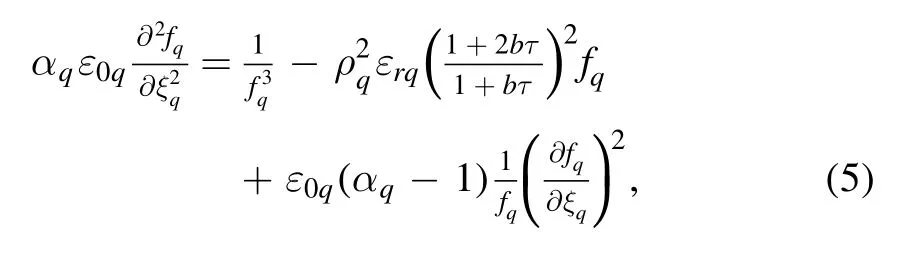
whereε(r,z)=ε0(z) − (r2/r02)εr(z)is the plasma effective dielectric function in the presence of the laser beams,ε0(z)=ε(r,z)|r=0,εr(z)=ρq=r0ωq/cis the equilibrium beam radius,ξq=zωq/cis the normalized distance of propagation,αq=1+bτ/andτis the dimensionless retarded time.Equation (5) is the second-order differential equation governing the laser spot size variation with the distance of propagation in the plasma.The first two terms on the right-hand side of equation (5)represent the diffraction and self-focusing of the pump laser phenomenon due to the relativistic ponderomotive nonlinearity,which has been assumed in this work.The last term reflects the presence of the frequency chirp.Equation (5)states that because of the coupling sentences,the treatment off1is dominated byf2and vice versa.

2.2.Dielectric function and density modification

In the relativistic regime,the quiver velocity of electrons is much greater than the thermal velocities,so we can assume that the plasma is cold.In this case,by assumingEq(q=1,2) as the amplitude of the electromagnetic wave,the effective dielectric function of such plasma can be written as[35]

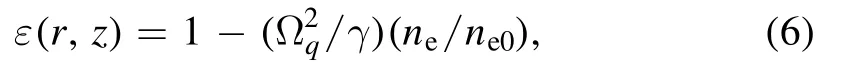
In order to obtain the rectified distribution of plasma electron density due to the presence of the laser beams,the set of motion equations along with the charge neutrality relation is used.In the steady state,the net static forces on electrons and ions must vanish as follows:

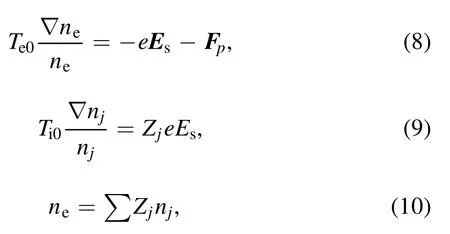
wherene0is the density of thejth variety of multi-ions,Esis the space-charged field,andTe0andTi0are the initial electron and ion temperatures.

By omittingeEsbetween equations (8) and (9),integrating the final equation for initial conditions,viz.EE*=0,ne=ne0andnj=nj0,and using equation(10),the moderated electron density distribution can be acquired as

whereη=Te0/Ti0,μ=me0c2/Ti0andnj0is the primary density for thejth type of ion.According to equation (11),the modified density of the electron can be estimated as a function of laser intensity.So,in the paraxial approximation,the effective dielectric function of plasma (see equation (6))can be expanded to the second order in the Taylor series aroundras follows:

where

Here,γ0=γ|r=0,neaandnerare respectively the axial and radial parts of the electron density distribution.It is essential to note thatneaandneronly depend on the propagation distance (z).

2.3.Nonlinear current density and THz generation

We consider two high-intensity laser beams(see equation(1))irradiating on a pre-formed rippled plasma with a density ofn=ne0+nr.nr=n′ exp (iκz)is the spatially periodic part of the density profile,in whichκandn′ are the wave numberωT(=ω1−ω2).The nonlinear oscillatory velocity at frequencyωTandkT(=k1−k2)can be obtained using the motion equation as follows:and the density ripple amplitude,respectively.The plasma density ripple can be created by applying a machining beam and a patterned mask[40,41].By adjusting the groove period and mask size one can control the ripple parameters.The plasma electrons experience the nonlinear time-dependent fluid ponderomotive force in beat wave frequency

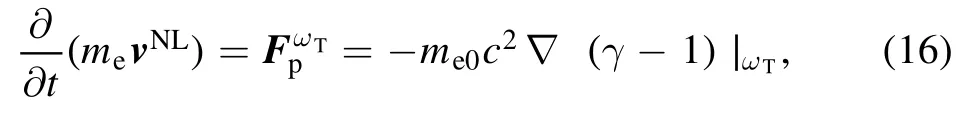
and comes out to be

The nonlinear current densityJNLat frequencyωT(which is responsible for the generation of THz radiation) due to the rippled density and the nonlinear velocity coupling can be written as

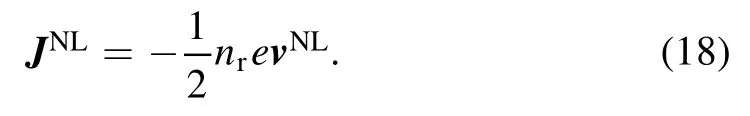
In order to obtain the THz electric field(i.e.ET),we used the evaluatedJNLin the wave equation

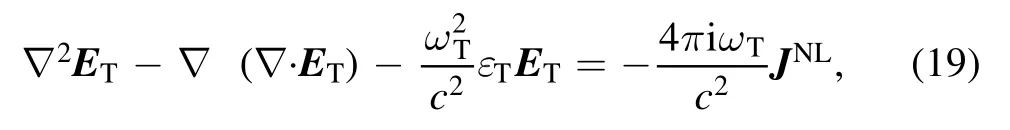
This is the expression for the amplitude of THz radiation.

Finally,we analyze the efficiency of THz generation.We examine the ratio of average energy densities of radiated THz waves and incident lasers (pumps).The time-average stored electric energy density is given by [42]

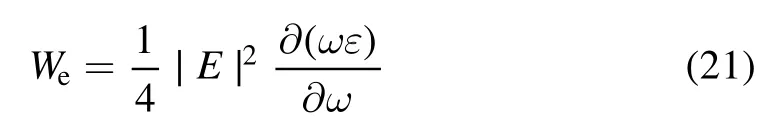
The energy (per unit area) of the pump lasers and THz radiation can be obtained as

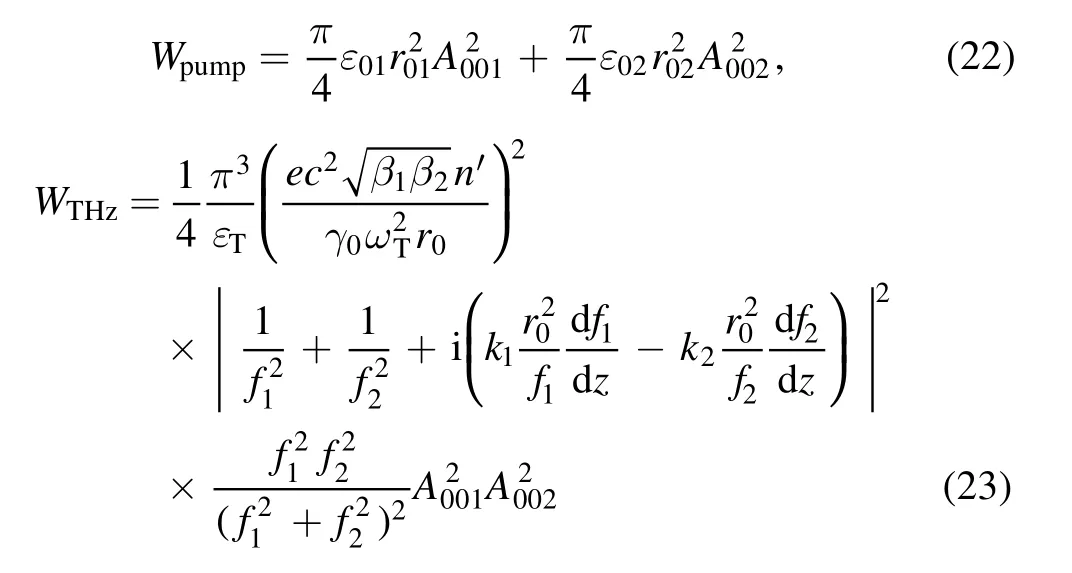
For simplicity,in calculations we assume thatA001=A002=A00,f1≈f2=fandr01=r02=r0.The efficiencyφof THz radiation generation is evaluated as

3.Numerical results and discussion

The equations governing the behavior of beamwidth parameters of chirped Gaussian laser beams in a multi-ion-species plasma as well as THz radiation generation are introduced in the previous sections by taking into account the relativistic ponderomotive nonlinearity.For more particular analysis of the effects of the chirp frequency and plasma multiple charged ions on the beamwidth parameters as well as the generation of THz,the set of equations(5)and(20)is worked outnumerically by fixingthe conditions as:a laserbeam(pump)with frequencyω0=1.77 ×1015rads−1(fora Nd:YAGlaserλ=1064nm)andpulseduration of1ps,r01(=r02)=20μmandI01(=I02)≈3×1017W cm−2propagated in the plasma withne0=1 × 1018cm−3,Te0=2.5 keV,n′=0.2ne0,η=1,j=2,Z1=1,Z2=2(e.g.hydrogen plasma embedded with helium) andn10=0.5ne0.We also used the initial conditionsf1,2=1anddf1,2/dξatξ=0.Figure 1 presents the effect of the chirp parameterbon the laser beam propagation as well as the generation of THz in the hydrogen-embedded helium plasma.Figure 1(a) shows the variation of the beamwidth parameterf1(one of the beams of the pump) with the dimensionless distance of propagationξ,forZ1=1,Z2=2,at different values of chirp parameterb.The other parameters are shown in the caption of the figure.It shows that in the absence of chirp,the regime of propagation of the beam is oscillatory defocusing,while the behavior of the beamwidth parameter was affected by taking into account the chirp frequency.If the value of the chirp parameterbis taken to be0.002 or0.004,the regime of propagation will be changed to the stationary oscillatory focusing mode due to the nonlinear effects and energy invariance included in this study.The periodic behavior of the beamwidth parameterf1along the distance of propagation causes oscillatory behavior of THz generation at the same distance(see figure 1(b)).Then if the chirp parameterbis set as0.025,the propagation regime occurs again in the defocusing mode,and the laser beam exhibits fast divergence.One can see that by increasing the value of the chirp parameterbup to0.004,the strength of self-focusing increases and the oscillation period of the beamwidth parameter gets lower.By increasing the value of the chirp parameterbfrom0.004 to 0.025,the self-focusing loses its strength and the beam is steadily diverged atb=0.025.By increasing the chirp parameterb,the amplitude of the beamwidth parameterf1reaches a minimum amount and then increases as the chirp parameter goes up.In other words,the propagating beam(pump) shows self-focusing up to a certain value ofband then the defocusing process is observed.Therefore,from the given figure,we can conclude that there exists a specified range for the value of the chirp parameterb,where the selffocusing mechanism can take place.We therefore chooseb=0.004as the optimum value of the chirp parameter for the present scheme.The results we obtained are in good agreement with the results obtained by Mehta et al[43].They found that the amplitude of the THz wave continues to increase until a specific chirp parameter (b=0.0099);beyond this value a negligible chirp appears and it is difficult to detect the chirp effect.Furthermore,Wani et al [33]investigated the effect of chirp on the beamwidth behavior of a Gaussian laser pulse in a collisional plasma for a small range of chirp parameter changes,and reported that once the chirp parameter is increased the strength of self-focusing increases.The normalized THz amplitudes for chirp parameters applied in figure 1(a) are plotted in figures 1(b)-(g)versus the normalized radial distance (r/r0) and normalized distance (ξ) along the propagation direction.It is noted from equation (18) that the output THz field is directly related to the spatial gradient of the pump laser intensity.The radial gradient of laser intensity for a Gaussian profile at the center of the beam is zero,then it begins to first rise and then fall along the radial axis.Thus,in the cross view one can see a ring-like shape for the THz intensity profile from figures 1(b)or 1(d).Figure 1(b) displays the variation of THz amplitude for zero chirp (b=0).The generated THz amplitude along the propagation direction shows the periodic shape corresponding to the periodic trend of the beamwidth parameterf1at the same distance.In comparison with figure 1(b) whereb=0,figure 1(d) shows that by considering the chirp frequencyb=0.004,the generation of THz radiation is increased due to the dominance of the nonlinear term in equation(5).However,further increase of the chirp parameter tob=0.025leads to significant weakening in THz emission as a result of the laser spot size widening (see figure 1(a) forb=0.025).This behavior may be explained as follows:increasing the chirp parameter increases the angular frequency of laser beams;as a result,the dielectric function (or refractive index) of the plasma increases,which leads to an increase of the self-focusing mechanism.Consequently the ponderomotive force increases by amplifying the laser intensity and expels the electrons out of the axial axes and makes the local electron density lower.For a certain value of chirp parameter(hereb=0.004),with further increase of the chirp parameterb,the number of expelled electrons out of the axial region increases and the rest of the electrons contained in the axial region play a less significant role in the selffocusing process,so the propagating beams start to experience the defocusing.Our results are in good agreement with those by Mehta et al [29,43]for the investigation of THz radiation with different values of chirp parameter.In addition,amplification of the second harmonic amplitude with the increase of chirp parameter has been reported theoretically by Thakur et al [44]and experimentally by Gou et al [45].The study of the dielectric function gradient (∇ε∝εr),which is responsible for self-focusing,could be useful to explain the beam evolution towards the increase of the chirp parameter value.In fact,according to equation (5),beam converging arises as a result of the dielectric permittivity gradient;hence,to observe the reason for the beam spot size behavior,the functionεrversus the chirp parameterbis plotted in figure 2 atξ=0.It can be observed that by increasing the chirp parameter,the value ofεrenhances sharply and then quickly begins to decline,and its maximum point corresponds to the strongest self-focusing.This means that there exists a specific range for the chirp parameter value at whichεrand so nonlinearity reach their maximum values.Out of this range,a downward trend is observed forεrby either decreasing or increasing thebparameter.So,the output of the THz emission can be tuned by choosing suitable values of the chirp parameter.

Figure 1.(a)Variation of the beamwidth parameter f1 with normalized distance of propagation(ξ)for different values of chirp parameter b,when(Z1,Z2)=(1,2)(i.e.hydrogen-embedded helium plasma),n10=0.5n e0and I01=3 × 101 7 W cm− 2.((b),(d),(f)) and ((c),(e),(g))3D and contour plots of the normalized THz amplitude for b=0,0.004and 0.025,respectively.

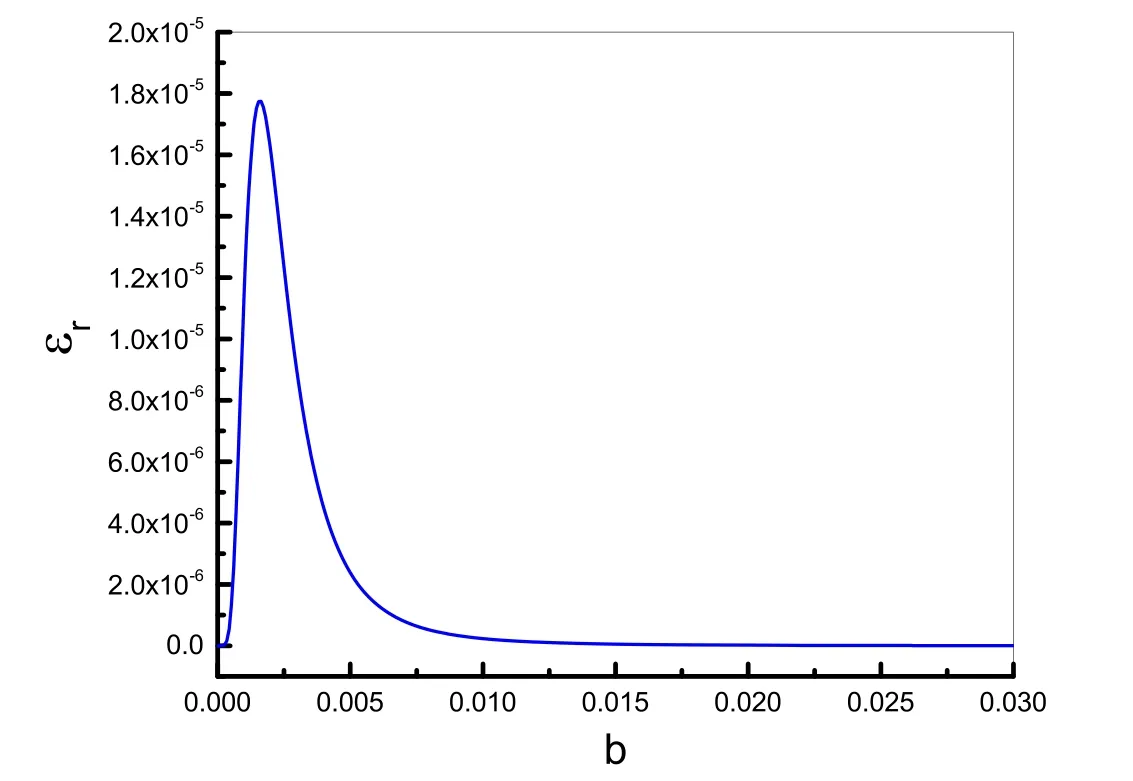
Figure 2.The function of εr versus the chirp parameter(b).The other parameters are the same as those in figure 1.

Figure 3.(a) Variation of the beamwidth parameter f1 with a normalized distance of propagation (ξ) for different values of initial laser intensity,when(Z1,Z2)=(1,2),n10=0.5n e0and b=0.004.((b),(d),(f)) and ((c),(e),(g)) 3D and contour plots of the normalized THz amplitude for I01=1 × 101 6 W cm −2,I01=3 × 101 7 W cm− 2and I01=1 × 101 8 W cm− 2,respectively.

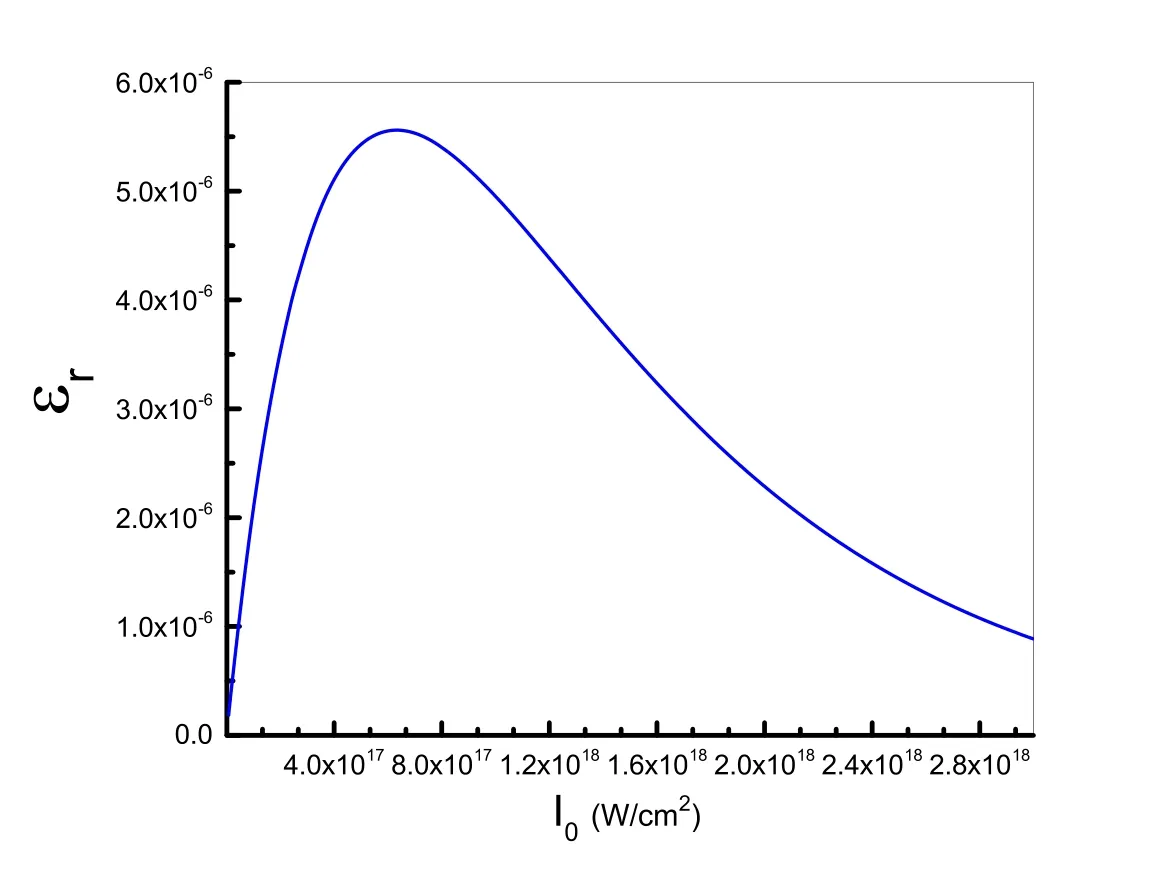
Figure 4.The function of εrversus initial laser intensity for different values of initial laser intensity for(Z1,Z2)=(1,2)and b=0.004.

In the following part,considering a constant chirp parameter(b=0.004),the effects of pump laser intensity on the Gaussian laser beam propagation as well as the generated THz radiation in the plasma including two ion species (for example,helium plasma embedded with hydrogen)have been studied.The normalized beamwidth parameterf1(one of the beams of the pump) and corresponding THz radiation curves versus normalized propagation distanceξ,for different pump laser intensities varied in the range ofI01=1016− 1018W cm−2are sketched in figure 3.It shows that the beamwidth parameterf1quickly increases and the steady divergence (the black dashed curve of figure 3(a))takes place in the case of low laser intensity due to the diffraction effect.Increasing the laser intensity value toI01=3 × 1017W cm−2,the propagation regime changes to oscillatory self-focusing mode.However,in the case of a more intense laser beam (I01=1018W cm−2),the beamwidth parameter increases slowly and self-focusing starts to attenuate (blue dash-dotted curve in figure 3(a)).A similar trend can be observed in THz emission by enhancing the laser intensity in figures 3(b),(d) and (f).By comparing figures 3(b) and (d) one can see a sharp amplification of the THz amplitude just by intensifying the laser beam by almost one order of magnitude.Meanwhile,a decreasing trend in THz amplitude is observed with higher laser intensity in a similar way to the beamwidth parameterf1behavior.This is because the amount of THz radiation is completely dependent on the strength of self-focusing.From figure 3,we can understand that the maximum yield of THz occurs in a distinctive range of laser intensities,then it saturates and finally reduces.Reinforcement and then weakening of the generated THz radiation by increasing the laser intensity has also been proved by experimental results [46].The present numerical results are in good agreement with the empirical data acquired by Oh et al [46].Furthermore,the present results can be compared with those of Lu et al[47].They reported that in a constant laser pulse duration,the THz amplitude increases and then saturates as the laser intensity increases.In our previous work [26],we also observed similar numerical results.We reported that,in a collisional plasma,there is a range for laser intensity with a‘turning point’,where the THz amplitude reaches its maximum strength,and outside of this range,it disappears.The physical description basically refers to the dielectric function change by the laser intensity as it has a direct impact on the beam evolution.For this reason,the curve of therεfunction versus laser intensity is plotted in figure 4.As figure 4 demonstrates,for a specific range of laser intensity,εrreaches its maximum and outside this range its value decreases.Accordingly,the self-focusing strength and yield of THz radiation appears stronger and more efficient by applying a particular laser intensity,and in other cases they are not optimal.

In the next step,in order to determine the effect of ionic species density on the evolution of laser spot size and thus THz generation,variations of the beamwidth parameter at different initial singly ionized species densitiesn10have been investigated in the weakly relativistic regime of our consideration.By taking into account a chirped Gaussian laser beam withb=0.002and constant initial intensity ofI01=3 × 1017W cm−2,the dependence off1onξfor various values from initial ratios of singly and correspondingly doubly charged ionic (Z2n20=ne0−Z1n10) species to the initial electron densityn10/ne0=0.1,0.5and0.9 and a contour plot of the normalized THz radiation intensity are plotted in figure 5.Figure 5(a) demonstrates that the behaviors off1for allthree valuesof (n10/ne0)are oscillatory converging.However,when increasing theratio (n10/ne0),which means that the plasma approaches the singly ionized state,the self-focusing is strengthened.Similarly,one can see a slight amplification of THz emission due to the enhancement of self-focusing strength by increasing the ratio(n10/ne0)(comparing figures 5(a)and(b)).In other words,the above results indicate that in the helium mixed hydrogen plasma,increasing the density of doubly ionized species reduces the nonlinearity,and subsequently the beam converges.In the physical interpretation,in the interaction of a Gaussian laser beam with plasma,nonlinear phenomena like the relativistic ponderomotive force modify the electron density distribution.The latter also leads to a change of dielectric permittivity and consequently causes the evolution of the laser spot size.In this regard,according to figure 5(a),the presence of multi-ions creates a stronger space-charge field in comparison with a singly ionized plasma,so that it restricts the redistribution of electron density.Therefore,the nonlinearity is weakened and the beamwidth parameter tends to get larger.In fact,within high-intensity laser interaction with a multi-ionized plasma,relativistic ponderomotive force plays an important role in the redistribution of electron density,so that modified electron density takes place as a result of the space-charge field and ponderomotive force reaction.To clarify the latter,figure 6 illustrates the dependence of the normalized electron densityne/ne0(i.e.equation(11))on the laser (pump) intensity in a multiple charged ion plasma for three different values ofn10/ne0.One can see from figure 6 that the value ofne/ne0monotonically decreases by increasing the initial laser intensity.This is easily understood due to the ponderomotive force related to the high-intensity laser,which pushes electrons (out off the axial region) more strongly and causes the space-charge field.Figure 6 also shows that for each constant laser intensity by increasing the singly charged ionic species density,the magnitude of electron density reduces.This confirms the previous results and means that by getting close to the singly ionized plasma condition (n10=0.9ne0),the nonlinearity appears partially stronger because of the slightly larger value ofne.The presence of ions with higher charges applies the stronger spacecharge field and so restricts the electron density redistribution.In other words,in the relativistic regime and multi-ion plasma conditions of our study,the created space-charge force prevents the self-focusing and makes it weak,while its strength is not enough to change the regime of propagation as the ponderomotive force is dominant for the latter.The present results are in agreement with results reported by Misra et al[35].

Figure 5.(a) Variation of the beamwidth parameter f1 with normalized distance of propagation(ξ)for different ratios of n10/ne0.(b) and (c) Contour plots of the normalized THz amplitude for n10/ne0=0.1and 0.9,respectively,when(Z1,Z2)=(1,2),b=0.002and I01=3 × 101 7 W cm− 2.

Figure 6.Dependence of normalized electron density(n e/ne0)on the initial laser intensity for different ratios of n10/ne0,when Z1=1,Z2=2and b=0.004.

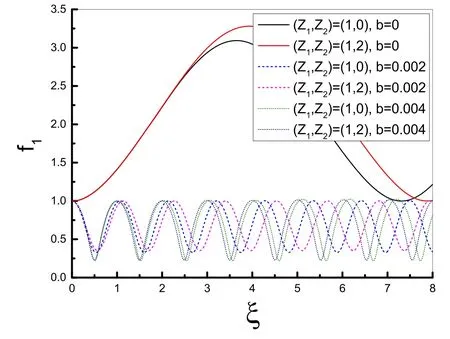
Figure 7.Variation of the beamwidth parameter f1 with normalized distance of propagation (ξ) for different values of Z2 and b,for I01=3 × 101 7 W cm −2.

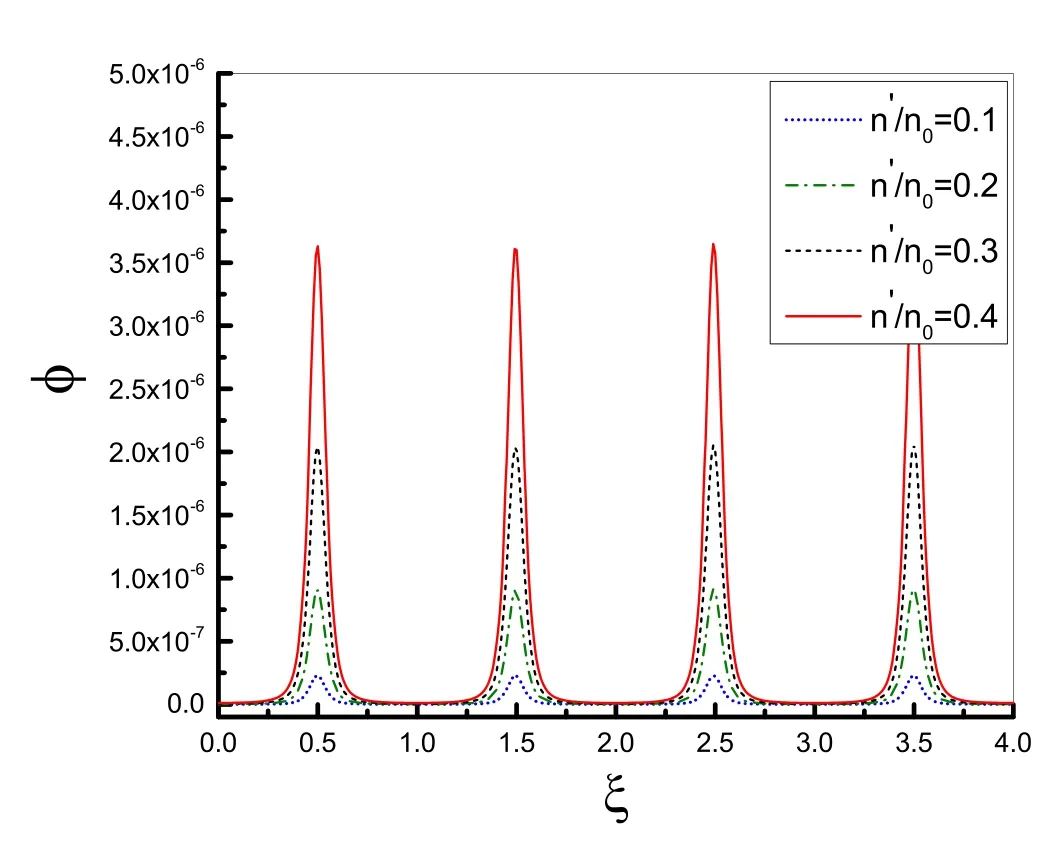
Figure 8.Variation of efficiencyφ with normalized distance of propagation (ξ) for different values of normalized density ripple n′,when(Z1,Z2)=(1,2),b=0.004and I01=3 × 101 7 W cm −2.

The propagation dynamic of laser beams(pumps)and the generation of THz radiation in the plasma when ions are only singly charged as well as singly and doubly charged have been compared with each other.The variation of the beamwidth parameterf1as a function ofξ,for three different values of chirp parameterb,in hydrogen plasma (Z1=1) and hydrogen-embedded helium plasma (Z1=1,Z2=2),is illustrated in figure 7.One can see that for each givenbvalue in the figure,by increasing theZ2value from 0 to 2,the oscillatory amplitude of the beamwidth parameter increases and its frequency decreases,which means that the strength of focusing decreases and the spot size of the laser beam increases and therefore THz generation decreases too.In other words,the existence of the ions with higher charge state(different than unity) has caused a decrease in the focusing strength and consequently a drop in the level of THz generation.This can also be understood from the description of figure 6,which was previously discussed.The reason is that a multiple charge causes a significant space-charge field and thus restricts the modification of electron density;this weakens the nonlinear influences and hence the self-focusing and THz generation.Finally,the dependence of efficiencyφon the ripple amplituden′is evaluated in figure 8.This figure shows that by increasingn′,the efficiencyφis increased significantly.So,the conversion efficiency of THz radiation is sensitive to density ripples.

4.Conclusion

In the present work,we have numerically studied the generation of terahertz radiation by the interaction of two copropagating frequency-chirped Gaussian laser beams with a multi-ion-species plasma,taking into account both weakly relativistic and ponderomotive nonlinearities.We investigated the effects of the plasma and initial laser parameters,such as the chirp frequency,ions of higher charge and initial intensity of lasers (pumps),on THz generation.It is shown that the laser beam propagation and the THz generation in the plasma are very sensitive to the frequency chirp,and this can change the regime of the propagation.It is demonstrated that the amplitude of the THz radiation cannot be continuously increased by increasing the value of the chirp parameter(b)or the initial laser intensity(I0).It is shown that for a given initial laser intensity (chirp parameter),the THz field amplitude has increasing/decreasing behavior as a result of an increase in the value of the chirp parameter(initial laser intensity).There are specific ranges for the frequency chirp and the laser intensity depending on the other initial conditions of the laser and plasma,where self-focusing and consequently THz generation can occur.Each of these ranges has a ‘turning point’where the THz generation reaches its maximum.Moreover,the effect of the presence of the singly and doubly ions on the evolution of the spot size of an intense frequency-chirped laser beam propagating in plasma has been studied.The selffocusing process of the cross-coupling of the beams and THz amplitude is enhanced as the ratio of the single ionized species to the elementary electron density increases,which is due to the enhancing of the nonlinear effects.Finally,the presence of the ions with higher charged states leads to a reduction of THz generation in the plasma because of the increase of the space-charge effect,which can restrict the electron redistribution.