Simulation study on electron heating characteristics in magnetic enhancement capacitively coupled plasmas with a longitudinal magnetic field

Haiyun TAN (谭海云),Tianyuan HUANG (黄天源),Peiyu JI (季佩宇),Lanjian ZHUGE (诸葛兰剑) and Xuemei WU (吴雪梅),∗

1 School of Physical Science and Technology&Collaborative Innovation Center of Suzhou Nano Science and Technology,Soochow University,Suzhou 215006,People’s Republic of China

2 Key Lab of Advanced Optical Manufacturing Technologies of Jiangsu Province &Key Lab of Modern Optical Technologies of Education Ministry of China,Soochow University,Suzhou 215006,People’s Republic of China

3 School of Optoelectronic Science and Engineering,Soochow University,Suzhou 215006,People’s Republic of China

4 Analysis and Testing Center,Soochow University,Suzhou 215123,People’s Republic of China

Abstract The electron heating characteristics of magnetic enhancement capacitively coupled argon plasmas in presence of both longitudinal and transverse uniform magnetic field have been explored through both theoretical and numerical calculations.It is found that the longitudinal magnetic field can affect the heating by changing the level of the pressure heating along the longitudinal direction and that of the Ohmic heating along the direction which is perpendicular to both driving electric field and the applied transverse magnetic field,and a continuously increased longitudinal magnetic field can induce pressure heating to become dominant.Moreover,the electron temperature as well as proportion of some low energy electrons will increase if a small longitudinal magnetic field is introduced,which is attributed to the increased average electron energy.We believe that the research will provide guidance for optimizing the magnetic field configuration of some discharge systems having both transverse and longitudinal magnetic field.Keywords: capacitively coupled plasma,longitudinal magnetic field,electron heating,PIC/

1.Introduction

The parameters of capacitively coupled plasmas(CCPs),such as plasma density and electron energy distribution function(EEDF),etc,play important roles in material etching or thin film deposition,and they usually depend on how electrons gain energy from driving electric fields,which is traditionally known as electron heating [1].

Ohmic heating is an important mechanism in electron heating,which origins from the collision between electrons and neutral particles [2].In this case,the synchronous relationship between the motion of the colliding electrons and the driving electric fields is destroyed,and therefore the electrons obtain net energy.In some cases,however,the strong power deposition in CCPs cannot be explained well by Ohmic heating,and there must be some additional ‘collisionless’mechanisms to heat electrons,as pointed out by Godyak et al[3,4].A classical model described collisionless heating is known as hard-wall model,which proposed by Lieberman[5].In this model,the electric filed in plasma zone is ignored,and the collisionless heating is considered as a result of the random interactions between the moving electrons and the oscillating sheath electric filed.Some further researches show that the strong electric filed reversals in the region between the sheath and plasma zone can also introduce additional collisionless heating [6,7],which is known as ambipolar electron heating [8].In addition,the electrostatic waves originated from the energetic electron beam propagating from the sheath edge toward plasma zone can also contribute to the collisionless heating in some cases [9].Another classical model proposed to understand the collisionless heating is known as the pressure heating model.In this model,the collisionless heating is considered to be related to the pressure action in electronic fluid [10,11].

To analyze the dependence of collisionless heating on discharge parameters,some analytical models have been proposed to describe the level of collisionless heating[6,12].These models,however,often show some errors when compare their results with that from particle-in-cell (PIC) simulations[13],and cannot describe all the physical mechanisms of collisionless heating completely.To determine the level of the heating accurately,Surendra and Dalvie proposed a quantitative method,in which a dynamic fluid model is used to analyze the heating,and parameters of this model are taken from simulations [14].Through this method,heating components from different physical mechanisms can be distinguished,and thereby which components are important can be determined.They further revealed that the pressure tensor of electrons is the physical origin of collisionless heating,and time-varying electron temperature is very important for this heating.Based on such a method,people have a clearer understanding of electronic heating in CCPs.For example,Lafleur et al found that the total heating in their most CCPs tested cases consists mainly of Ohmic heating and pressure heating,with the additional collisionless heating associated with the electron inertia being negligible[15].Liu et al found that the thick dielectric sidewall in CCPs can enhance the level of the axial Ohmic heating and result in the increase of axial electron density[16].Schulze et al found that the strong bipolar electric fields are very important for pressure heating in electropositive CCPs[17],and Proto et al further expanded this conclusion to electronegative CCPs recently [18,19].

If one introduces a transverse magnetic field which oriented parallel to the electrodes into CCPs,then the electron heating as well as plasma characteristics of the CCPs may be modulated [20].For example,transverse magnetic field can enhance the level of Ohmic heating significantly,and induce the Ohmic heating to become dominant in total heating[21,22].In addition,the electrons near the magnetized plasma sheath edge can undergo periodic cyclotron motion,and in some cases the couple between the oscillating sheath and the cyclotron electron can enhance the electron heating,which is known as electron bounce-cyclotron resonance heating[23-25].On the other hand,some quantitative studies about the influences of transverse magnetic field on electron heating in CCPs have also been reported.For example,Wang et al found that with the increase of transverse magnetic field,the dominant heating mechanism in magnetized oxygen CCP will translate from electronegative drift-ambipolar heating to electropositive stochastic electron heating [26].Zheng et al revealed that the transverse magnetic field induced Hall currents play important roles in enhancing the level of Ohmic heating in CCPs [27].

In summary,a series of accurate quantitative researches have discussed the effects of transverse magnetic fields on the electron heating in CCPs,few studies,however,report the effects of longitudinal magnetic fields on that in CCPs.In this work,the electron heating characteristics in a magnetic enhancement CCP with a longitudinal uniform magnetic field are explored through both theoretical and numerical calculations.This paper is structured as follows.In section 2,a dynamic fluid model used for analyzing the electron heating characteristics is reviewed.The simulation model used to perform numerical calculations and its parameter setting is described in section 3.The effects of longitudinal magnetic fields on electron heating characteristics are stated in section 4.The last part is a summary of the full text.

2.Theoretical background

For a magnetized plasma,the first momentum Boltzmann equation for electrons is the momentum balance equation,read as [28]

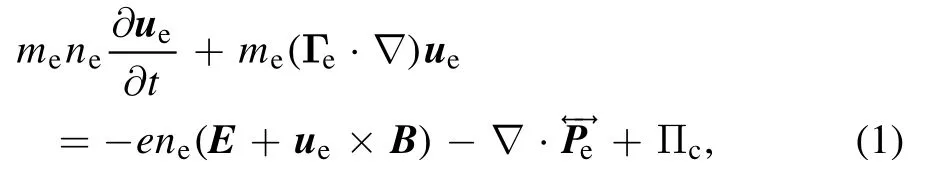
wherene,ueand Γerepresent the density,mean velocity and flux of electrons,respectively.E and B represent driving electric fields and applied magnetic fields,respectively.represents the pressure tensor of electrons andΠcrepresents the momentum change resulting from electron-neutron collisions.Since elastic collision is dominant in the electronneutral collisions,theΠccan be obtained by subtracting the electron momentum before elastic collision from that after elastic collision.In this work,we take electron positions at integral time oftand electron velocities at half integral time oft+Δt/2to calculate Πc,a more detailed discussion of Πccan be found in Lafleur et al [15].Multiplying equation (1)with the mean velocityue,the new equation can be expanded as follows,

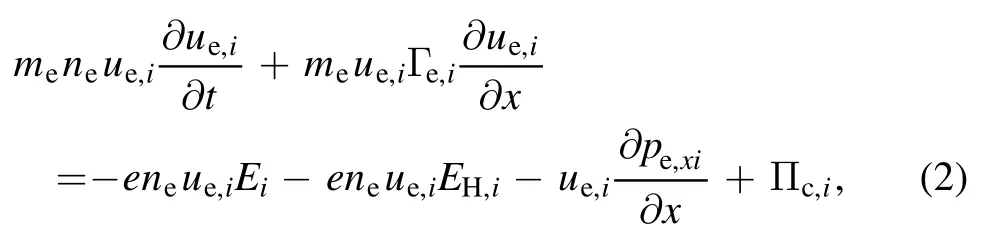
where the subscripti=x,y,zandEH=ue×Brepresents Hall fields.pe,xi=mene(〈vx vi〉 −u x ui)represents the elements of the pressure tensor,wherevrepresents velocities of the electrons.The term−eneue,i Ei=Pabsrepresents the level of the electron heating.In the case of a one-dimensional(1D)plasma with a driving electric field ofE=(Ex,0,0),Pabsobtained from equation(2)can be expressed in two forms,i.e.the heating in x-direction including magnetic field term

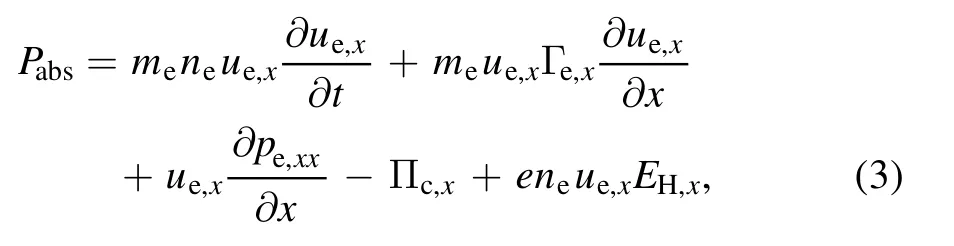
or the heating in global space excluding magnetic field term,Pabs=Pin+Ppress+Pohmic,where

represent the level of inertia heating,pressure heating and Ohmic heating,respectively.In the following studies,Pinis ignored since the time averagedPinis usually unimportant [15].

3.Simulation descriptions

In this work,an implicit 1d3v PIC/MCC code is used to perform all the simulations,and the code has been benchmarked with the results from Zheng et al[24]and the results from Yang et al [29].We consider a magnetic enhancement CCP discharge system operated in argon,as shown in figure 1.In this model,we assume the working pressure and gas temperature are 100 mTorr and 300 K,respectively.The transverse magnetic fieldByis a fixed uniform magnetic field,while the longitudinal magnetic fieldBxis a tunable uniform magnetic field.The driving electric fieldExis generated by a voltage source having a waveform ofV~=V0cos (2πft),whereV0=300V andf=13.56MHz.The gap between the electrodes is 2.5 cm,and we have 80 equal cells in this gap.

In all simulations,we consider electron-neutral collisions and argon ion-neutral collisions,where the collision types and the collision cross sections are shown in figure 2.The cross sections of electron-neutral collisions are taken from[30],in which for elastic electron-neutral collision the momentum transfer cross-section is used,and all scattering events are treated as isotropic,as referred as [17].The crosssections of argon ion-neutral collisions are taken from [31],and elastic ion-neutral collision is isotropic,while the ion after the charge exchange collision (backscattering collision)has a velocity equal to the velocity of the neutral atom that collides with the ion.The velocities of particles after collision events are calculated by the method in [32].

The initial electrons and ions have Maxwell distributions with temperatures of 2 eV and 0.026 eV,respectively,and have a uniform profile in the gap.When the simulations reach a steady state,there are about 60 000-80 000 super-electrons(the number of super-ions is similar).We use a double-timescale algorithm in all simulations,that is,the time step of electrons and that of ions are 1 × 10−10s and4 × 10−10s,respectively.The secondary electron emission process is not considered here to simplify the analysis and it will not have a significant impact on our main conclusions.All simulations run for 5000 radio frequency (RF) periods and take about 3000 periods to reach a steady state.The macroscopic quantities,such asne,peand electron temperatureTe,etc,are calculated by a linear weighting scheme [33],and their time averaged value in 1500 RF periods are taken as the input parameters for the fluid model described in section 2.

4.Results and discussions

Evolutions ofneat different uniformBxare shown in figure 3(a),where the fixed uniformByis 50 G.It can be seen that the globalnedecreases gradually with the increasedBx,which implies a weakened electron heating.Figure 3(b) further demonstrates evolutions of the peakneand the averagednewithBx.WhenBxincreases from 0 to 40 G,the peaknedecreases from2.65 × 1016to 1.05 × 1016m−3,while the averagednedecreases from 1.4 × 1016to0.47 × 1016m−3,both electron densities decrease.AsBxcontinues to increase,however,the rates of decrease of both electron densities slow down gradually,which indicates that there is a limit to the effect ofBxon the heating.

Figure 1.The model of the magnetic enhancement CCP operated in argon.

Figure 2.The collision cross sections used in simulations,which are taken from [30,31].

Figure 3.Evolutions of ne versus different Bx,where By is 50 G.(a) Global electron density,(b) peak electron density as well as averaged electron density.

Figure 4 shows evolutions of the total heating profile〈E x·Jx〉 with differentBx,whereJx=−eneue,xrepresents current density in x-direction andeis unit charge.The figure also showsPabsas well as the different heating components calculated from equation (4).It can be seen that the results from the theoretical calculations agree very well with those directly from numerical calculations in all cases.Meanwhile,Ppressis negative in the plasma zone,and oscillates at the sheath boundary,whilePohmicmakes an important contribution to the heating in plasma zone,and it reaches a maximum near the sheath region.AsBxincreases continuously,the level of all these heating components decreases gradually,and the heating in plasma zone tends to be negligible.

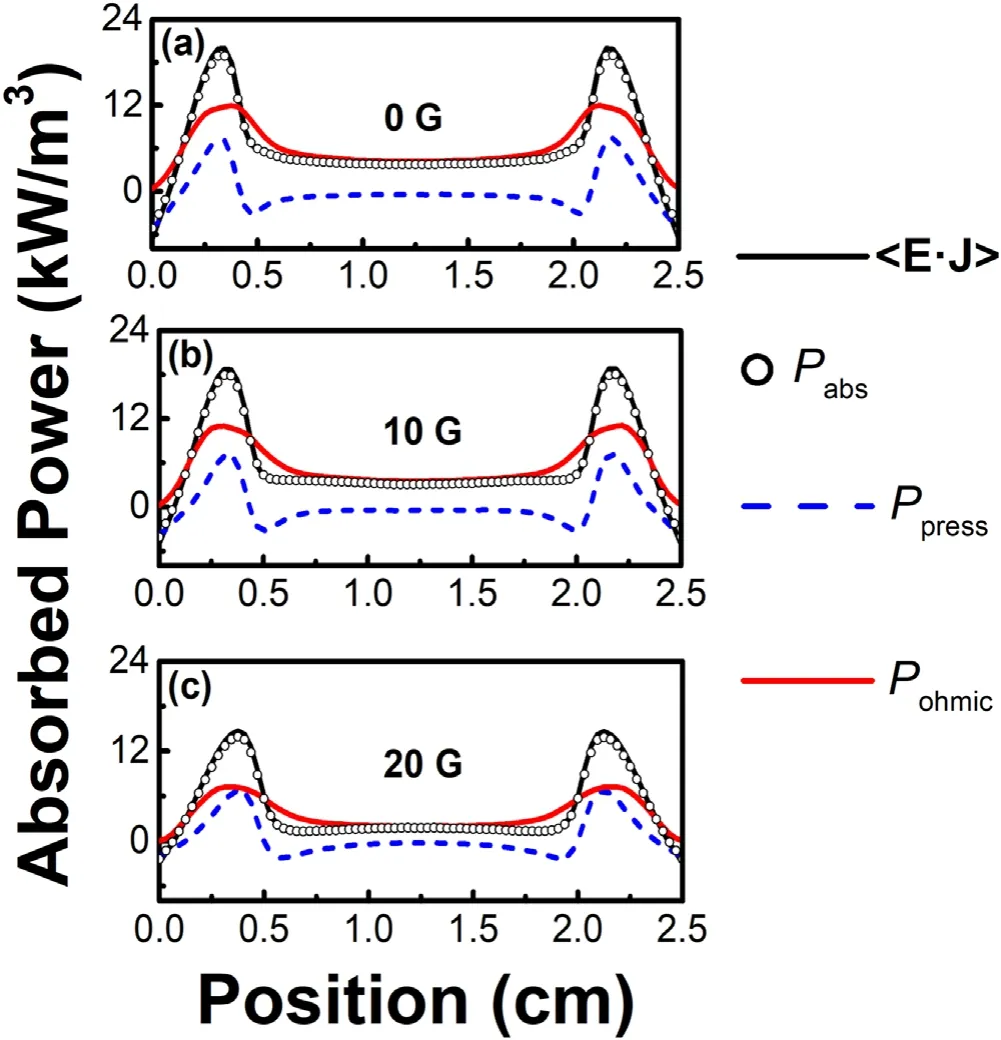
Figure 4.Evolutions of both the total heating profile and each heating component profile versus different longitudinal magnetic fields.(a) Bx=0G,(b) Bx=10G,(c) Bx=20G.

The phenomenon ofBx-induced reduction in the heating is related to the electron confinement in the z-direction.It can be seen from equation (3) that the total heating can be expressed as a sum of a series of heating components in xdirection,i.e.Pabs=Pin,x+Ppress,x+Pohmic,x+eneue,xEH,x,where the termeneue,xEH,xcan be considered as a magnetically induced heating [26].With the increasedBx,the Hall fieldEH,xdecreases since the increasedBxconstrains electrons more so thatue,zdecreases [2],and this results in a reduction in the level of the heating.On the other hand,asBxcontinues to increase,the termeneue,xEH,x=−eneue,xue,z Byis expected to be negligible sinceue,ztends to zero,which can explain why there is a limit to the effect ofBxon the heating.

Figure 5 shows the spatio-temporal evolutions of the total heating as well as that of different heating components at differentBxin one RF periodic.It can be seen from figures 5(a1)-(c1)that the electrons near the sheath boundary lose and gain energy periodically with the oscillating sheath,and the loss of energy is correlated highly with the energy loss caused by pressure heating mechanism during sheath collapse,as shown in figures 5(a2)-(c2).Electrons gain energy in two main ways,that is,energy gain caused by pressure heating mechanism during sheath expansion and that caused by Ohmic heating mechanism during entire RF cycle.In addition,the Ohmic heating reaches maximum near the sheath boundary when the sheath begins to expand or the sheath collapse is about to end.Finally,with the increase ofBx,the level of all heating decreases.Interestingly,when a smallBxof 10 G is introduced,the Ohmic heating in front of the sheath boundary is enhanced when the sheath begins to expand,and this phenomenon disappears with the further enhancement ofBx,as shown in figures 5(a3)-(c3).

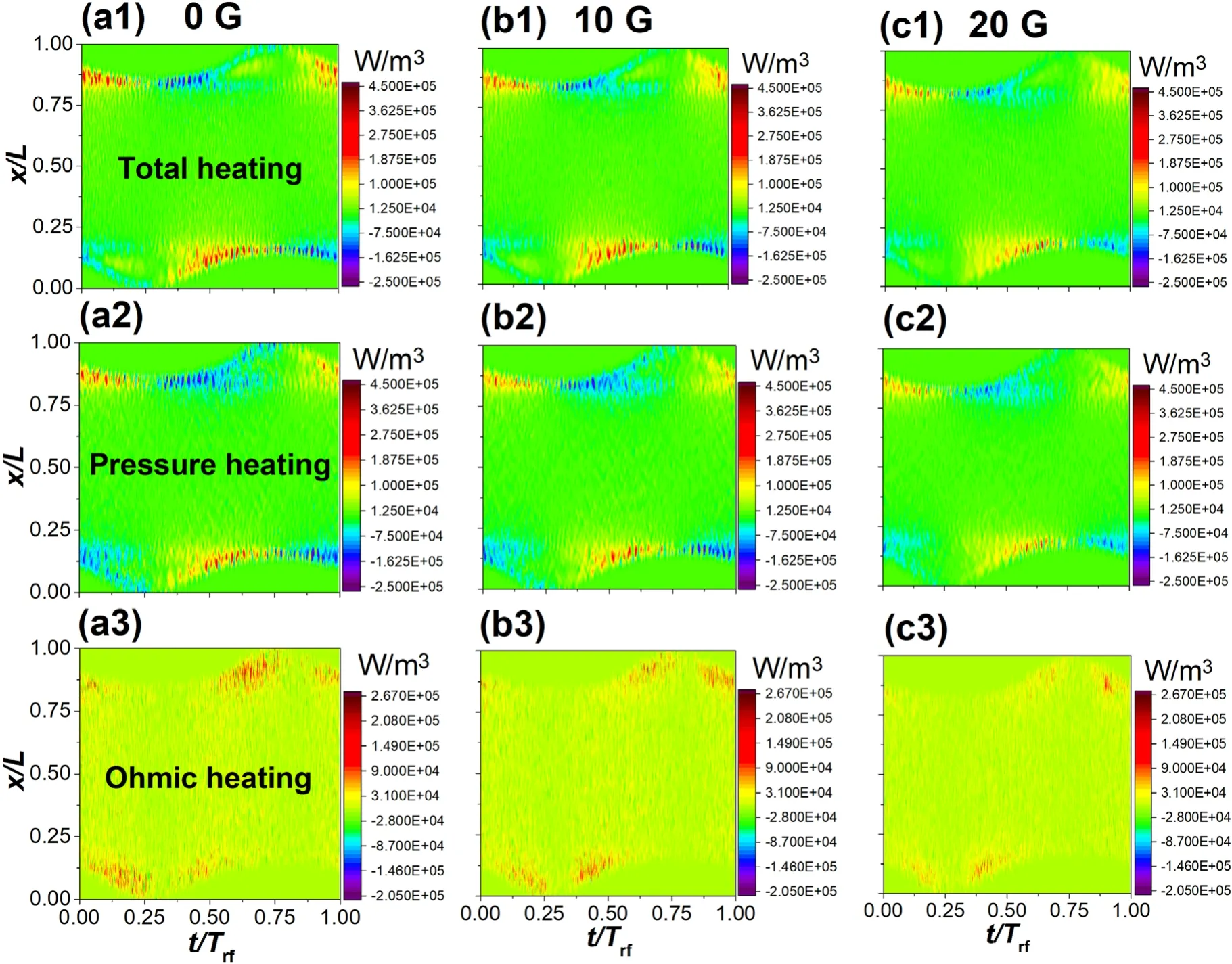
Figure 5.The spatio-temporal evolutions of both the total heating and different heating components at different Bx in one RF periodic.(a) Bx=0G,(b) Bx=10G,(c) Bx=20G.

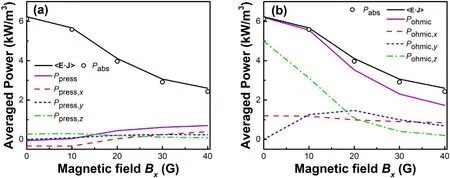
Figure 6.The evolutions of the spatio-temporally averaged heating components with different Bx.(a) Pressure heating,(b) Ohmic heating.

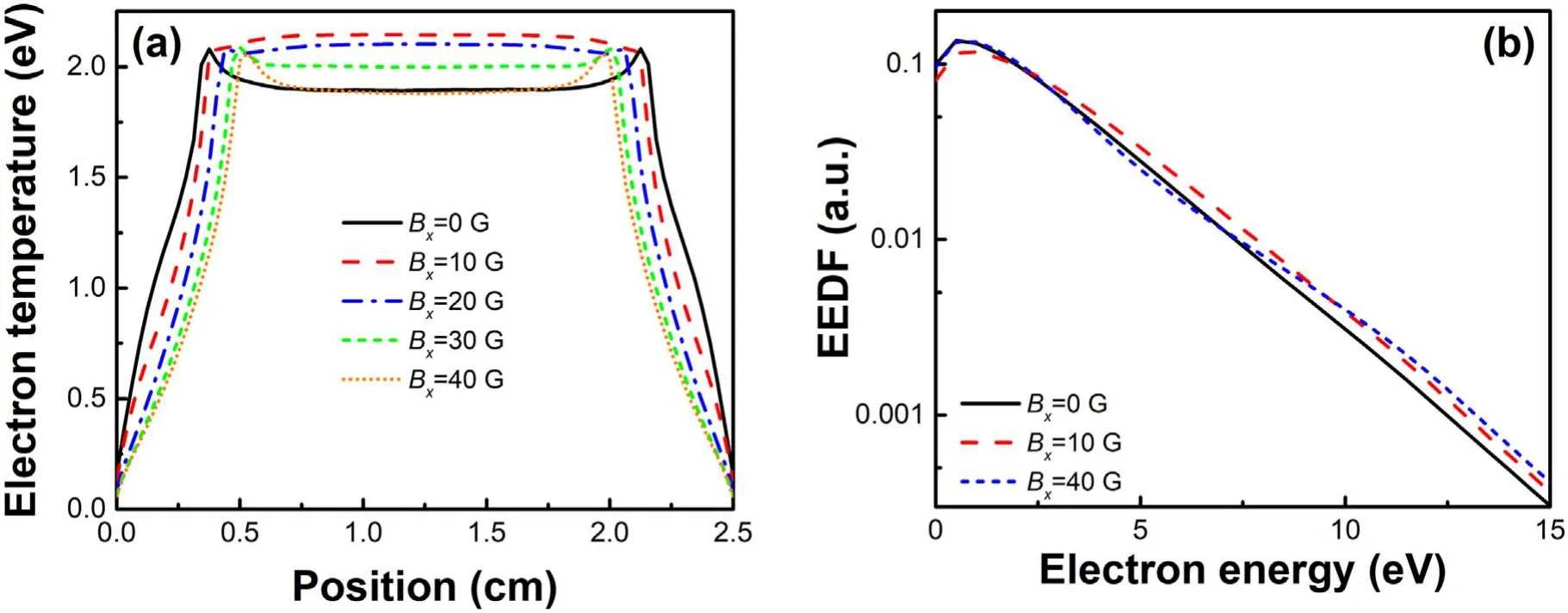
Figure 7.Evolutions of Te as well as that of the global EEDF versus different Bx.(a) Electron temperature distribution,(b) global EEDF.

Figure 8.Evolutions of loss rates of both the spatio-temporally averaged electron density and the spatio-temporally averaged electron absorbed power versus different Bx.

To further analyze the influences ofBxon the heating,figure 6 shows the evolutions of both the spatio-temporally averaged total electron heating(includes〈E·J〉andPabs)and each heating component.It can be seen that the total heating decreases with the increasedBx,and tends to be stable,which is consistent with the change inneshown in figure 3.Meanwhile,the decreased total heating is correlated highly with the weakened Ohmic heating,as shown in figure 6(b).In addition,asBxkeeps increasing,the level of the Ohmic heating decreases gradually while that of the pressure heating shows an opposite trend,which implies a transition in the dominant heating mechanisms from Ohmic heating to pressure heating whenBxincreases gradually.

On the other hand,figure 6 also shows howBxaffects the heating components.It can be seen that whenBx=0,PpressandPohmicare zero in the y-direction.WhenBx＞ 0,however,net heating in the y-direction appears,which arises fromBx-induced Hall electric fieldEH,y.In addition,asBxincreases,Ppress,xandPpress,yshow an upward trend,whilePpress,zshows a downward trend.It is clear that the varying pressure heating is correlated highly withPpress,x.Meanwhile,Pohmic,xchanges little withBx,whilePohmic,yfirst increases and then decreases,andPohmic,zshows a downward trend.The varying Ohmic heating is correlated highly withPohmic,z,and the weakenedPohmic,zis attributed to the reduced Hall currents along ‘E × B’ direction [27].Here the ‘E × B’ direction is referred as a direction which is perpendicular to bothExandBy.Now,by analyzing the level of different heating components,it is confirmed thatBxaffects the electron heating mainly by changing pressure heating along the longitudinal direction and by changing Ohmic heating along the ‘E × B’direction.

The influences ofBxon plasma characteristics are also explored,as shown in figure 7,which shows the evolutions ofTeas well as that of global EEDF at differentBx.As can be seen from figure 7(a),when a small(10 G in this work)Bxis introduced,Tein plasma zone increased sharply,and then decreased gradually with the continuously increasedBx,which results in the spatial profile ofTeevolving from bimodal-like to inverted U-like and then back to bimodal-like.

Meanwhile,the global EEDF shows a similar change.When a smallBxof 10 G is introduced,the proportion of a considerable part of low energy (about 2.5-15 eV in this figure) electrons in the EEDF increases,which means that electrons become ‘hotter’.AsBxfurther increases to 40 G,however,the proportion of most low energy(about 2.5-9 eV)electrons decreases significantly,while the proportion of some lower energy electrons (about 0-2.5 eV) increased slightly,as shown in the blue dotted line in figure 7(b).As a result,the electron temperature decreases.

To understand the dramatic change in bothTeand EEDF caused by the smallBx,figure 8 shows evolutions of loss rates of both the spatio-temporally averaged electron density and the spatio-temporally averaged electron absorbed power at differentBx,where the benchmark data are the plasma parameters atBx=0.It can be seen that whenBx＞ 10G,the two loss rates rise at almost the same speed and tend to be stable.However,whenBx≤ 10G,the change in the loss rate of the averaged absorbed power is not as intense as that of the averaged electron density.For example,whenBx=10G,the loss rate of the averaged absorbed power rises from 0% to 9.113% (9.113%/10 G),while that of the averaged electron density rises from 0%to 22.14%(22.14%/10 G).In this case,electrons are lost quickly,while the total electron heating remains at a relatively high level,and results in most of the electrons gaining more energy.As a result,the electron temperature and proportion of some low energy electrons in EEDF increase.

5.Conclusions

In summary,the electron heating characteristics of a magnetic enhancement CCP in presence of both longitudinal and transverse uniform magnetic field have been explored by using a combination of theoretical and numerical calculations.It is found that the electron density as well as level of the total heating decreases gradually and tends to be stable with a continuously increased longitudinal magnetic field,which results from the confinement of electrons in the direction which is perpendicular to both the driving electric field and the applied transverse magnetic field(a direction referred to as‘E × B’ direction in this work).Further analysis shows that longitudinal magnetic field affects the heating mainly by changing pressure heating along the longitudinal direction and by changing Ohmic heating along the‘E × B’direction.As longitudinal magnetic field increases continuously,the level of the Ohmic heating decreases gradually,and the pressure heating tends to be the dominant heating mechanism.Finally,it is worth mentioning that when a small longitudinal magnetic field is introduced,the electron temperature as well as the proportion of some low energy electrons in the EEDF increases.This is because the small longitudinal magnetic field causes a significant decrease in electron density but remains a relatively high level of the electron heating,which results in more energy per electron.Although the analyses in this paper are based on 1D simulations,these research conclusions,however,are still expected to be effective in 2D cases [34],and can provide guidance for optimizing the magnetic field configuration of some discharge systems with both transverse and longitudinal magnetic fields introduced.

Acknowledgments

This work is supported by National Natural Science Foundation of China (Nos.11975163 and 12175160),a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).