较高流速下泡沫金属内流动传热特性的孔尺度模拟

汤怡恺，王 会，，徐 强

(1.东华大学环境科学与工程学院，上海 201620；2.西安交通大学动力工程多相流国家重点实验室，陕西 西安 710049)

随着航天航空活动的日益频繁与其国家战略地位的不断提高，高速飞行器动力系统成为了航天领域的一个重要制约因素[1].自英国REL公司提出Skylon计划[2]，预冷式组合循环动力系统SABRE(协同吸气式火箭发动机)就成为动力系统研究的重点，该预冷器能在极短时间内将管外略空气自1 000 ℃降低至-150 ℃[3].但由于预冷器中极细的换热管束，易造成冷却剂泄露结霜且需要很高的工艺精度.泡沫金属隶属超轻多孔介质，具有蜂窝状结构、高导热系数以及较大的空腔体积，能够根据需求优化结构设计[4，5]，且拥有较好的抗压强度与抗冲击特性[6]，现已成为散热器和紧凑型热交换器优良的候选材料[7]，在航天航空领域拥有较好的应用前景；但其复杂的孔隙结构为探究内部流动带来诸多不便，高速下多孔介质的强化传热机理并不完善.而计算流体力学(CFD)随同计算机的发展，变革性的转变了流体力学实验的思路与方法[8]；将数值模拟应用于泡沫金属，基于拓扑结构的模拟实验是更加简便高效的研究手段.

目前研究者对模拟泡沫金属内部流动已取得相应成果.本文作者[9，10]曾研究了不锈钢泡沫填充管0 m/s～26 m/s下流动传热特性，指出泡沫金属的渗透率和惯性阻力与速度区间具有较大相关性.Hamidi等[11]运用CT(微计算机断层扫描技术)建模计算了雷诺数Re(Reynolds numbers)在50～1 000条件下泡沫金属三维强制对流换热特性；Yu等[12]采用CT建模并计算了流速为0.5 m/s～2.5 m/s范围内各项异性特征参数，模拟结论得出骨架结构将影响泡沫金属实际流动压降情况.Yang等[13]采用W-P结构研究了较低Re下不同旋度Ro(Rotating number)对间隙努塞尔数Nu(Nusselt number)的影响，并给出不同Re、Ro、ε(孔隙率)及流动通道位置与Nu之间的关系式.Corsini等[14]运用直接数值模拟研究了ε=0.92泡沫金属在Re=4 000条件下的紊流尾迹，得出速度波动受各向异性的影响比许多标准网格湍流研究的更大.此外研究者们也提出了多种泡沫金属简化结构借以研究多孔介质内部流动换热；Calmidi[15]和Bhattacharya[16]等建立了二维六边形蜂窝状的金属泡沫简化结构模型，并对其有效换热系数进行推导；Lu等[17]以简单立方体为单胞的周期性结构来模拟金属泡沫的微观结构，分析得到了金属泡沫骨架直径、孔胞直径、相界面比表面积等结构参数的理论表达式；杨肖虎等[18]研究了十四面体通孔泡沫铝有效导热系数与孔隙率的线性关系；Du Plessis等[19]将金属泡沫的孔胞结构简化成三维立方体结构并结合泊肃叶流动的假设，提出了预测金属泡沫内压降的理论模型；黄媛媛等[20]采用通孔六面体对流速在0 m/s～10 m/s下泡沫金属对流换热性能进行评估.

综上，目前泡沫金属多研究其在较低流速下的流动情况，但对于较高流速下流动研究较为薄弱，复杂多孔介质中的高速对流换热机理尚需加深，这对泡沫金属在航空领域的应用具有重要意义.本文以十四面体为基础建立拓扑模型并进行三维数值模拟，运用Fluent模拟得到计算域中温度场与压力场分布云图，分析流速与孔密度对泡沫金属综合换热性能的影响.探究较高流速下多孔金属的压降阻力参数沿流速的变化趋势并导出泡沫金属流速-压降拟合公式，进一步考察了多孔介质内对流换热机理.

1 泡沫金属模型构建

1.1 孔胞结构几何模型

本文以十四面体构建单胞模型并生成拓扑结构，结构参数依测量所得[21]；图1为金属孔胞结构，其孔径大小为dp，整体高度为H，并给出整体结构.

图1 单胞及整体结构

本试验建立孔隙率ε=0.97，孔密度分别为10、20、30及40PPI的泡沫金属模型进行数值模拟.泡沫金属结构孔隙率ε由公式(1)得出；不同PPI所对应的孔隙直径如表1所示.

表1 不同PPI泡沫金属孔隙参数

(1)

1.2 边界条件与控制方程

本试验采用Fluent进行数值模拟，选用三维稳态模型进行模拟试验，得到在不同工况下的泡沫金属结构的流动情况与传热情况，并提出如下假设：

(1)由于本模拟温度最大值为323 K，其辐射换热量不足总换热量的5%，因此忽略热辐射对整体传热过程的影响；

(2)流动过程中泡沫金属及流体不随温度变化而发生物性参数的改变；

(3)由于在高速流中，空气介质与泡沫金属表面充分接触，能够达到流固相界面温度相等，因此忽略流体介质与泡沫金属间的接触热阻；

(4)当Ma<0.3时，将流体工质视为不可压缩流.

本文选用标准湍流模型Standardk-ε研究流体与泡沫金属骨架间的流动传热关系，其控制方程为

(2)

(3)

并给出能量方程：

(4)

为确定试验数据可靠性，验证采用与前人相同试验边界：即低温空气流体流经高温泡沫金属区域，具体边界条件如下：空气介质的温度为293 K，在泡沫金属壁面设置定壁温，流经模型的空气温度将会提升.材料设置为铝；区分为入口边界与出口边界：入口边界给定平均流速，温度给定293 K；出口则为压力出口，表压为0；上壁面给定绝热壁面条件，下壁面设定恒定温度323 K；流体左右两侧设定为对称面；采用SIMPLE算法，压力项采用PRESTO！，即预压交错选项，能够给予交错面控制量，其余采用二阶迎风格式；本次试验流体与固体的参数如表2所示.

表2 材料参数

1.3 数学公式

本文主要描述不同工况下泡沫金属流动场分布，其雷诺数定义为

(5)

关于泡沫金属的对流换热系数h由如下定义为

(6)

公式中：Ac为通道横截面积；ρf为流体空气密度；Cp为流体定压比热容；Tout与Tin为进出口的平均温度；A为流体与壁面的换热面积；并给出对数平均温差LMTD，其中ΔTout=Tsolid-Tout，ΔTin=Tsolid-Tin，Tsolid为泡沫金属骨架面的平均温度.

定义传热因子j，该值越大，泡沫金属模型则具有较好的对流换热效果：

(7)

定义阻力因子f，该值越小，模型便能够减小流动阻力所带来的损失：

(8)

2 模型验证

2.1 网格划分及无关性检测

为得到良好的数据结果，现进行网格无关性检测.验证孔密度为10PPI，孔隙率为0.97，整体计算域为(9.42×9.42×22.29)mm的泡沫金属非结构网格模型，网格划分如图2所示.

图2 网格划分

本试验计算三套网格数，数量分别为：923 330，1 661 807，3 849 535；无关性结果如图3所示，得出网格数为1 661 807下的泡沫金属模型数据精确且网格资源消耗适中，确定以1 661 807网格数进行模拟研究.

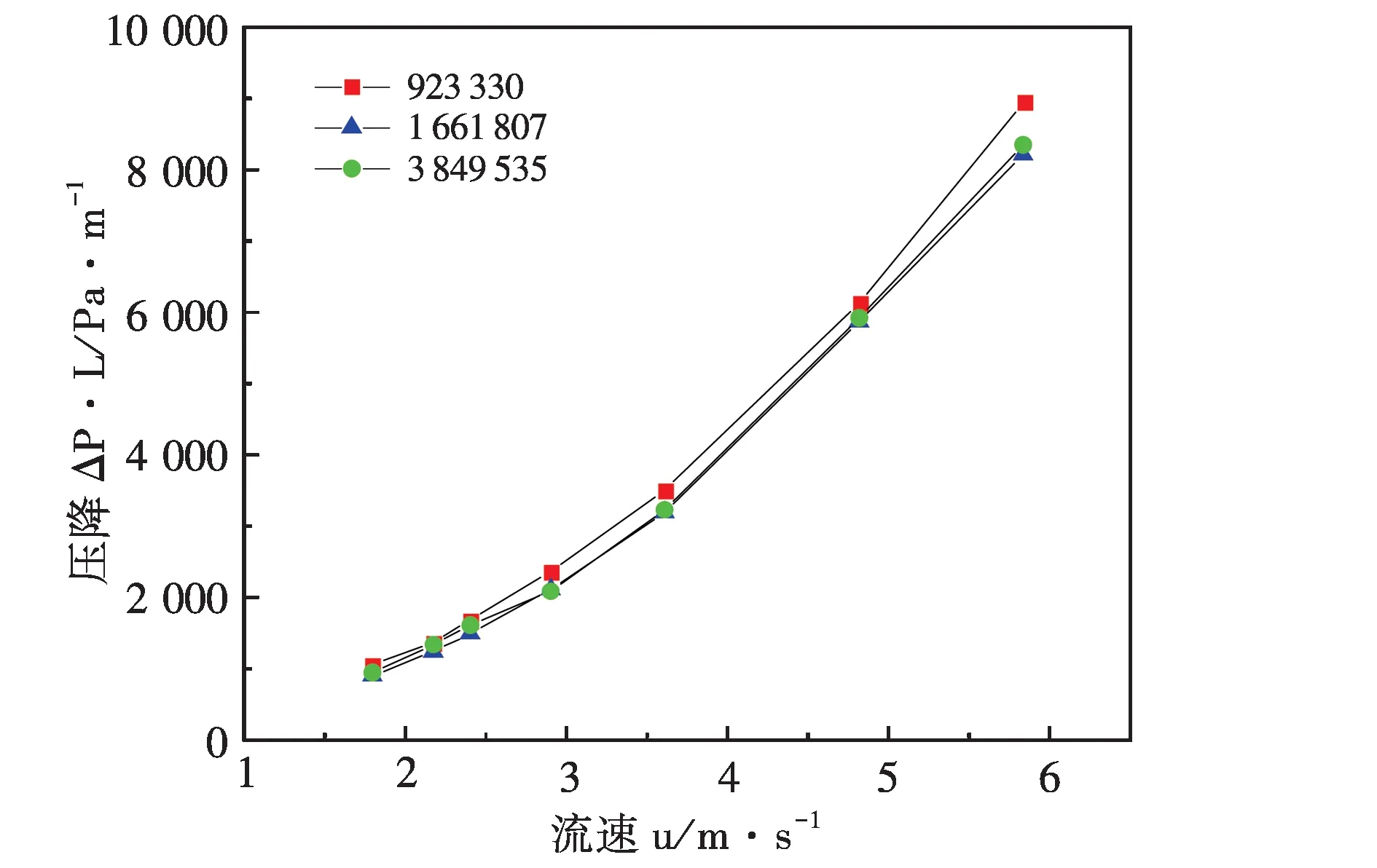
图3 网格无关性分析

2.2 模型验证

为验证该模型计算的精准度与正确性，将计算结果与Alvarez等[22]试验数据和Kopanidis等[23]的W-P模型的模拟数据进行对比，采用孔密度为40PPI的泡沫金属.不同单胞结构参数具有差异，结构参数对比如下表3所示.

表3 结构参数对比

本文模拟了不同流速下对应的泡沫金属骨架压降与对流换热系数，并与文献数据进行对比，结果如图4所示；本试验十四面体模型较Alvarez[22]试验数据的压降最大误差约为14.93%，Konpandis[23]模拟数据压降较Alvarez[22]试验数据的压降最大误差约18.12%；而本试验对流传热系数较试验最大误差为13.32%，Konpandis[23]所得系数的最大误差则为34.81%；即该模型能够反映实际流体在泡沫金属中的流动情况.结果得出孔隙率为0.97，孔密度为40PPI的泡沫金属对流传热系数与试验相比同样具有较好的一致性，能够较为精确的复现实际试验条件下得到的结果.

图4 40PPI下泡沫金属模型验证

3 模拟结果与讨论

3.1 泡沫金属温度场和压力场分布

图5给出了不同流速下泡沫金属在中心截面及骨架处的温度场，压力场和速度场分布情况.由图5(a)可知，在293 K空气流体流经恒壁温的泡沫金属后，前侧骨架将流体分束，由于与泡沫金属骨架对流换热，使得泡沫金属周围温度上升，在出口阶段温度达到峰值.根据图5(a)、图5(d)、图5(g)可知，流速越高，壁面侧温度边界层厚度减小，流体温度上升幅度变小，流体进出口温差减小，导致流固相之间温差增大，换热性能增强.图5(b)、图5(e)、图5(h)给出了泡沫金属在流动过程中压力分布情况；空气工质在接触泡沫金属骨架前端产生压力并使流线分流，在骨架后端产生局部压力损失，且由于十四面体结构周期性建模，其压力下降较为均匀，骨架后半段流体产生负压，随后在流体出口处实现归零.图5(c)、图5(f)、图5(i)给出流速云图及流线图，其中高流速区流线分布密集，流体经骨架分束后形成高流速区.显然流体在泡沫金属骨架结构处造成较大压力损失，可以显著增加泡沫金属换热效果.对比云图可得流速对前端骨架压力影响较大，流速越高，计算域中流体紊乱度越高，泡沫金属骨架所受压力越大，所造成的流动阻力也越大.造成流体压降的原因有两个：一是由于流体与模型骨架之间的局部流动损失，二是由于流体与骨架壁面之间的摩擦力.

图5 泡沫金属温度场和压力场分布

3.2 流动压降及拟合公式

图6给出了不同PPI下整体计算域的压降变化.由下图可得，不同孔密度的泡沫金属所受压降皆随流速增大而增大；在流速相同情况下，高PPI泡沫金属的压降高于低PPI泡沫金属压降，这是由于高孔密度的泡沫金属具有更小的孔隙直径，使多孔介质流动阻力增大；模型骨架间对流体绕流的加强同样导致流动损失增大.当流速为30 m/s时，40PPI泡沫金属压降数值较10/20/30PPI分别提高了218.72%，123.87%，66.55%，当流速为80 m/s时，10PPI压降便达到MPa/m.显然泡沫金属在高流速下内部流动紊乱度较高，且在高孔密度中其压降变化更加剧烈.

图6 不同PPI泡沫金属压降对比

为研究十四面体泡沫金属流动压降规律，探究流速与整体压降之间的联系，将泡沫金属内压降表示为速度二次拟合公式为

(9)

其中：

(10)

(11)

公式中：a，b分别为与渗透介质与流体有关的经验参数；u为流动速度；dh为水力直径；ε为孔隙率.

定义水力直径dh，如公式(12)所示.

(12)

其中Sv为单位体比表面积，运用几何方法可得到泡沫金属中该参数解析值：

(13)

公式中：dwin为泡沫金属侧边孔径，即十四面体剖球后侧边小圆孔径.

综上，图7给出孔隙率ε=0.97的泡沫金属在不同PPI条件下所对应的水力直径，并进行曲线拟合，同时参考Dietrich等[24]相关公式，得到孔隙率ε=0.97十四面体开孔泡沫金属水力直径的拟合修正公式(14).

图7 PPI-水力直径dh拟合曲线

dh=0.05 227PPI-0.7376.

(14)

由于研究者所选泡沫金属物性参数与试验条件不同，得到的实验数据存在差距，获得拟合公式经验系数同样有所差别.现对公式(9)泡沫金属压降公式进行参数拟合.得到在不同工况下ε=0.97的十四面体泡沫金属拓扑结构压降随流速及PPI变化(10-40PPI)拟合公式(15).

(15)

为验证拟合公式准确性与可行性，现将Dietrich[25]在较低流速下泡沫材料试验压降拟合公式代入并得出压降预测值，与本文提出有关高流速下泡沫金属压降预测公式进行对比，得到孔密度为40PPI下压降误差分析，如图8所示.由下图可知，在低流速范围内与本文拟合公式所得的压降参数具有较好一致性，但由于原拟合公式仅适用于0 m/s～10 m/s流速下多孔介质压降预测，在高流速下则会出现误差大于15%的情况.

为进一步验证本文压降预测公式准确性，取谢等[26]较高速流下孔隙率为0.95，孔密度为10PPI数值模拟数据进行对比，如图9所示.由图9可以得出该拟合公式预测数据与谢等[26]数值基本一致，在较高流速条件下10PPI泡沫金属拟合数值最大误差为12.23%，造成误差的原因可能是由于低孔隙率造成多孔介质空腔体积减小，使得谢等[26]压降数据略高与本文拟合公式.综上，本文拟合公式在高压条件下具有一定的适用性，能够预测较高速流下多孔介质内部流动压降损失，完善了泡沫金属内部流动机理研究.

3.3 流动传热综合分析

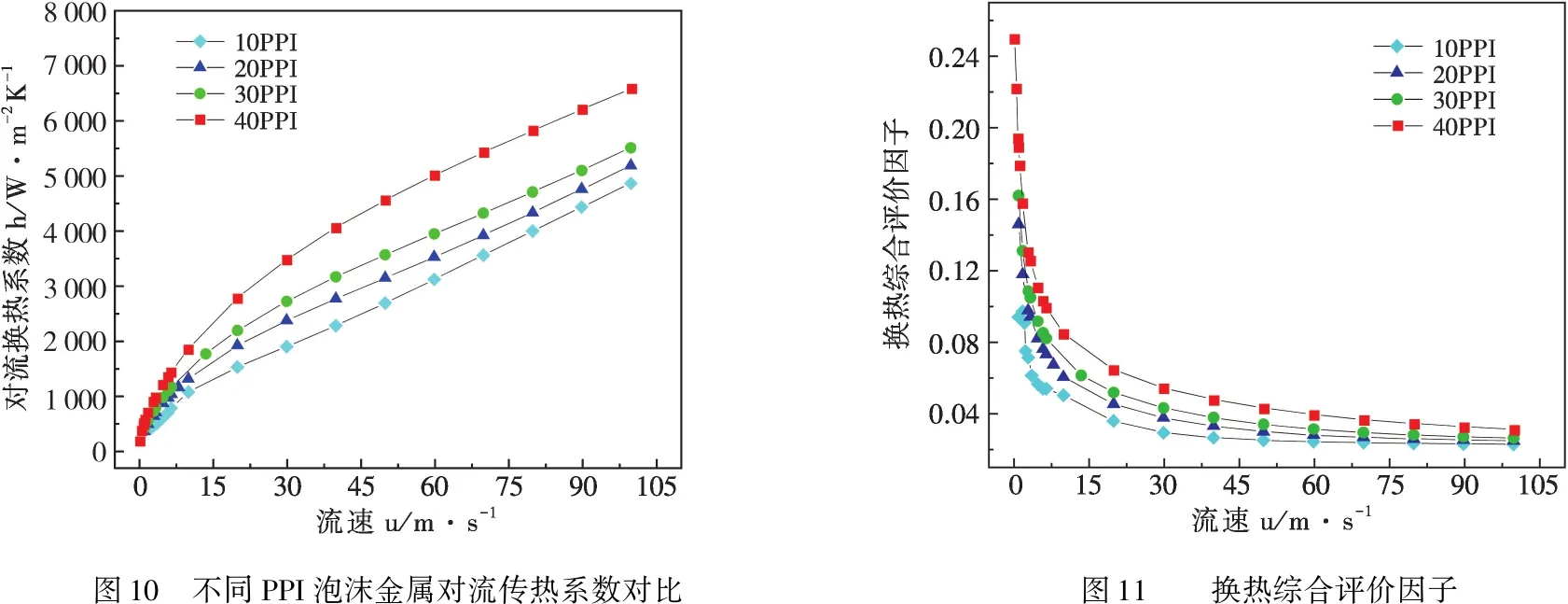
图10给出不同孔密度下泡沫金属内流速与对流换热系数的关系图.由图10得出，在流速相同时，泡沫金属孔密度越高则对流传热系数越大；当流速为30 m/s时，40PPI泡沫金属对流换热系数相较10/20/30PPI提高了84.09%，46.93%，27.92%.但在流速提高下差值变化不大，且对流换热系数在高流速下增长呈放缓趋势；在多孔介质中增大流速对提升换热性能影响程度不及对压降提升的程度.

本文以j/f^1/3评价泡沫金通道的综合换热性能，称j/f^1/3为换热综合评价因子，该值越大，代表泡沫金属多孔介质换热性能越好.由图11得出不同PPI下泡沫金属换热综合评价因子随流速变化趋势：在恒壁温边界条件与流速相同条件下，泡沫金属模型孔密度越大，则综合评价因子越大；但该因子随流速增大呈下降趋势，预计将降低至某一收敛值，说明泡沫金属换热性能随流速的增加无法抵消高流速下多孔介质结构所导致的压降阻力提升，造成泡沫金属通道的综合换热性能下降.得出结论：泡沫金属孔密度与流速对换热系数与压降都能造成影响，但显然流域内的压降受流速影响程度更大；对于相同孔密度下的泡沫金属而言，其流速越高，换热综合评价因子越低；孔密度为40PPI的泡沫金属在所选四种多孔介质中具有最佳的综合换热性能，这一现象在低流速下能够更加直观的体现.

4 结 论

本文运用Solidworks构建了泡沫金属十四面体拓扑结构，并导入Fluent进行网格划分及边界设定，随后对不同流速下泡沫金属流场宏观参数及流动情况进行验证分析.得到如下结论：

(1)对不同流速场下泡沫金属进行数值模拟试验，研究了较高流速下泡沫金属微结构流动传热特性，得到泡沫金属流动压力场及温度场.泡沫金属骨架在高流速条件下，壁面侧温度边界层厚度减小，流体进出口温差下降，导致流固相之间温差增大，换热能力与传热性能增强.矩形通道中流体紊乱度随流速与孔密度增大而增大，骨架结构所受压力越大，因此所造成的流动压降阻力也越大.

(2)在较高流速条件下，通过分析不同孔密度下多孔介质整体压降分布，得到孔隙率ε=0.97，孔密度为10-40PPI泡沫金属压降随流速变化的二次拟合公式.并与文献预测公式与模拟数据进行分析对照，证实其在低流速下与预测公式具有较好的一致性，且拟合公式与模拟数据的最大误差为12.23%，证实该公式的准确性与适用性，为泡沫金属在较高流速下压降阻力损失预测提供参考.

(3)研究了泡沫金属在不同孔密度与流速下整体换热性能.即在流速相同时，泡沫金属孔密度越高则对流传热系数越大；由于在多孔介质中，增大流速对提升换热性能的影响程度不及对压降提升的程度，因此对流换热系数在高流速下增长呈放缓趋势；同理，换热综合评价因子也随流速增大而降低并将达到某一收敛值.其中孔密度为40PPI的泡沫金属在10-40PPI中具有最佳的综合换热性能，在低流速下表现更加出色.