基于LMB滤波器高斯混合实现的传感器控制方法*

廖 晨

（兰州理工大学电气工程与信息工程学院 兰州 730050）

1 引言

标签多伯努利滤波器（Labeled Multi-Bernoulli，LMB）［4～5］作为多目标跟踪滤波器中的“集大成者”，是最具有研究意义和实用价值的滤波器算法。它是在有限集统计理论下（Finite set statistics，FISST）［2］，依据多假设思想，在多伯努利滤波器基础上引入标签向量，有效加强了目标与航迹之间的关联，避免了监测区域内当目标数目过多时，由于目标之间交叉、重叠而导致的航迹融合等问题，并直接解决了跟踪过程中目标之间无法区分识别的难题，且避免了复杂的数据关联，因此受到了广泛关注。

同时随着多源信息融合技术的发展，传感器控制方案的合理选择对于提升多目标整体跟踪系统的量测信息获取质量具有极大的现实意义，因此，多目标跟踪中的传感器控制问题成为了广大学者的研究焦点。一般而言，传感器控制方法是在部分可观测马尔可夫决策过程（Partially Observable Markov Decision Process，POMDP）［9～10］的理论框架下进行研究的，它的核心思想可概括为根据一定的最优控制准则，建立可供参考同时便于量化的目标评价函数，通过控制所选定传感器的运行参数和动作方式，最终动态地选择出使评价函数达到最优的传感器控制方案，从而确保最大程度地获取最优的量测信息。信息时代的到来，促使多目标跟踪技术迅猛发展，而复杂多变的现实跟踪环境，使人们对其提出了更高的要求。因此当传感器控制方法应用于大型跟踪场景时，例如军事打击及战略防御领域时，由于战场多元化的军事技术导致了海量数据的出现，因而利用有限的传感器资源最大化地获取监控区域信息，以及如何提高传感器的控制效率和降低传感器运行成本的要求成为亟待解决的问题。因此，在上述背景条件下，研究多目标下的传感器控制方法可以大幅提升多目标跟踪系统的整体性能，这对于信息融合领域的发展具有深远意义。

本文重点和主要创新点是通过LMB滤波器的高斯混合（Gaussian Mixture，GM）实现方式，提出两种基于信息论的传感器控制方法。首先给出LMB滤波器的高斯混合实现过程；其次详细推导了柯西施瓦茨（Cauchy-Schwarz）［7～8］散度在 LMB滤波器高斯混合实现下的评价函数解析解；同时为有效降低计算复杂度，利用多伯努利参数替代标签多伯努利参数进行“去标签”的伪更新方法得到基于CS散度的传感器控制方案；此外，基于战术重要性标绘（Tactical Significance Map，TSM）函数［21］，提出以最大威胁度目标信息增益最大化为准则的传感器控制方案；最后构造仿真场景对比验证所提控制方案的有效性。

2 理论基础

2.1 GM-LMB滤波器

LMB滤波器，它是GLMB滤波器在特殊近似条件下的滤波算法。在GM-LMB滤波过程中，可以利用多个带标签的独立伯努利运动过程的加权形式来近似描述多目标的概率密度分布，而每个伯努利过程的概率密度可以通过一组加权形式表达的高斯分量去实现。

因此，滤波过程中先验概率密度可以通过GM形式近似如下：

2.2 基于信息论的传感器控制方案

本文的研究内容均是在POMDP理论框架下展开的，其中基于信息论的传感器控制算法相关的核心要素可定义如下：首先，v是k时刻A12=A1+A2中所容许的任意一种控制方案，每一个v均对应传感器下一时刻的新位置。其次，pk(Xk|Z1:k)表示k时刻基于之前时刻累积量测信息下的多目标后验概率密度函数。最后，通过建立评价函数R(v)来衡量传感器的控制效果。因此，最优的控制序列可表达为

评价函数R(v)表达为

由上式可看出，R(v)是用来衡量两个概率密度函数之间差异性大小的评估指标，其中，fk+H(X|Z1:k)和fk+H(X|Zk+1:k+H(u))分别表示多目标的先验、后验概率密度函数，Zk(v)是每一种控制方案v对应的理想量测集合。

3 基于柯西施瓦茨散度的传感器控制方法

柯西施瓦兹（Cauchy-Schwarz，CS）散度［20］在一定程度上可看作一种用来度量两个集合之间距离大小的评估指标，可综合衡量系统整体的信息增益变化程度。

本文为了降低在滤波更新步骤中的计算复杂度，采用“去标签”的处理办法，将预测步骤中带标签的多伯努利参数集的标签丢弃，利用多伯努利参数替代标签多伯努利参数，进行传感器控制的伪更新，通过评价函数计算确定最终控制方案，之后传感器在新的位置接收到实际量测信息，再进行LMB更新步骤。

CS散度的评价函数表达如下：

“去标签”的伪更新过程中将预测部分的标签多伯努利参数集中的标签丢弃，无标签的预测多目标概率密度则可表示为

无标签的多伯努利参数集在一定程度上可等同于MeMBer滤波的参数集，因此，可套用MeMBer滤波器的滤波过程。预测的多目标概率密度参数集可表示为

通过Zk(v)对预测的无标签概率密度函数更新，得到多目标概率密度近似表达式：

参照运用两个高斯分量的乘积表达式，即

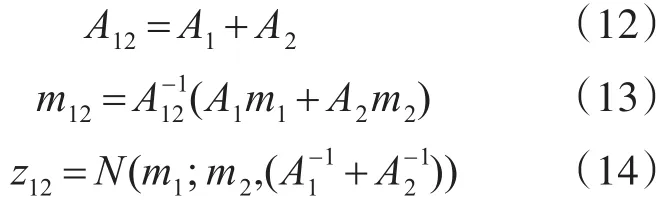
最后参照文献［15］，评价函数式（5）可推导为

且zij和zjj′的计算过程类似于上式。通过式（15）可计算得到R(v)，从而确定最终的传感器控制方案uk，传感器在当前时刻的控制位置xs，k(uk)可以接收实际量测集合Zk(uk)。

4 基于目标威胁度评估的传感器控制方法

TSM函数作为战术重要性评估指标，因其综合考虑了在目标运动状态中影响不同时刻目标威胁程度的各种因素。因此，本节采用TSM函数来衡量各种目标运动因素对战场重要性评估指标的贡献程度。该方法全面且合理考虑了多种威胁因子的非线性关系，核心因素包括目标的速度、航向及目标与传感器之间的相对距离。

综上考虑，由目标运动状态构建而成的威胁度评估指标TSM函数的最终表达式如下：

5 仿真实验

5.1 仿真场景设置

选 定[- 1000m，1000m] ×[- 1000m，1000m] 为监控区域，并在该区域中构造场景对目标进行跟踪，假设实验过程中目标最大数量为4个。量测采样周期为T=1s。场景中目标运动状态通过近常速运动模型来描述，状态转移密度可表示为

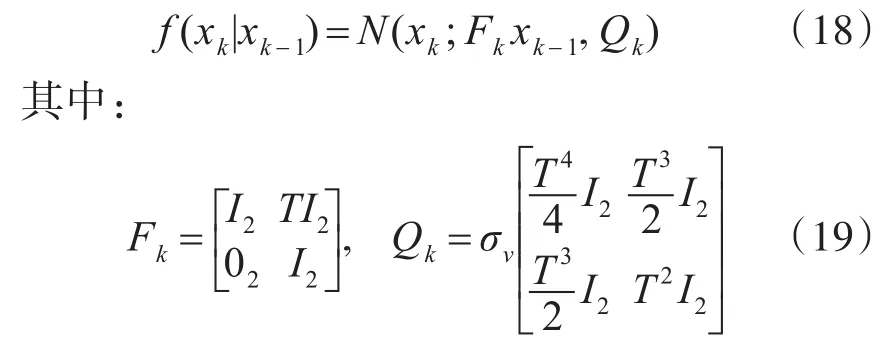
Fk为状态转移矩阵，Qk为噪声协方差矩阵，In代表n×n的单位阵，σv=5m/s2。目标运动状态（位置、速度）为，目标的存活概率为pS，k=0.99，检测概率pD，k=0.98。新生目标可用随机有限集的形式来表达，包含的多目标概率密度集合为。

5.2 传感器控制集合

实验中只在传感器所有允许的控制方案内进行选择。用xs，k=[xs，k，ys，k]T表示k时刻传感器所处的位置，按照“一步预测”理念，用Uk+1表示下一时刻传感器所有容许的位置集合，那么：

实验中选择NR=2，Nθ=8，因此共有17种可能的传感器控制方案（包含传感器在初始位置保持静止的情况）。

5.3 仿真结果分析

仿真实验中共选取五种传感器控制方案进行对比，并且对每种方案分别进行100次蒙特卡罗仿真实验。其中，方案一为“Stationary”控制方案，此方案令传感器在初始位置始终保持静默状态。方案二为“Prior zigzag”控制方案，即传感器按照预先设定好的轨迹运动。方案三为“Random control”控制方案，即在当前时刻中从传感器所有允许的控制方案中随机选取一种。方案四为“Proposed CS control”的方案，即基于GM-LMB滤波器，通过求解先验、后验概率密度之间的CS散度为目的的传感器控制方案。方案五是“Proposed Threaten control”的方案，即通过计算各个时刻每个目标的TSM值，选取最大威胁度目标，从而实现以最大威胁度目标的信息增益最大化为传感器控制准则的控制方案。实验中选用OSPA距离来衡量多目标优化算法的跟踪性能，设定c=100m，p=1。

根据构建的仿真场景，实验中多目标的新生与消亡时刻、初始位置和速度等参数分别如表1所示。

表1 多目标参数

图1给出了多目标真实运动轨迹及单次蒙特卡罗估计的跟踪结果，总共有四个目标，其中目标新生、消亡时刻分别标注为方框和五角星。由图可知，多目标整体跟踪效果良好。

图1 多目标运动轨迹图

图2为方案二“Prior zigzag”中传感器运行轨迹图，即传感器按照图中预先设定好的轨迹运行。图3为多目标整体系统位置估计的OSPA距离图，由上图中可以看到，所提出的方案四、五的跟踪精度明显好于其余三种方案，同时，又以方案四效果最佳，这是因为“Proposed CS control”方案在跟踪目标时优先考虑多目标系统的综合信息增益，是以整体信息增益最大化为原则的控制方案。而“Proposed Threaten control”方案则只注重跟踪威胁度较大的目标，没有兼顾区域内其余威胁度较小的目标运动带来的信息增益，因此对于系统所有目标跟踪的性能不如方案四。综上所述，“Proposed CS control”方案是针对系统整体跟踪的最优传感器控制算法。

图2 方案二中传感器运行轨迹图

图3 多目标整体系统位置估计OSPA距离图

表2为在滤波更新过程中通过“去标签化”伪更新后的传感器控制方案和原始方法的平均运行时间对比，表3则为OSPA距离均值的对比。结合两表数据，可以看出，在保证跟踪精度性能的前提下，采取“去标签”的伪更新方法，可以降低滤波过程的计算复杂度，提高运行效率。

表2 传感器控制方案单次平均运行时间表

表3 OSPA距离均值对比

图4为“Proposed CS control”方案的传感器运行轨迹图，是基于系统整体信息增益的控制方案。由上图可知，随时刻推移，传感器运行轨迹趋势会发生变化，这是因为在滤波过程中伴随着目标的新生和消亡，会影响到跟踪系统的整体信息增益，为了在每个时刻获取最优的量测信息，传感器会通过调整自身的位置，尽可能始终处于最佳的观测位置，从而实现以信息增益最大化为准则的控制目的。

图4 方案四中传感器运行轨迹图

图5和图6为基于威胁度目标的传感器控制轨迹，其中叉号代表每个时刻威胁度最大的目标。

图5 方案五中传感器运行轨迹及最大威胁度目标图

图6 方案五中传感器运行轨迹放大图

在初始时刻，监控区域内只存在两个目标，即目标一和目标二，目标一朝向远离传感器中心位置的方向移动，而目标二朝向传感器中心位置运动，但由于运动目标速度与距离的因素影响，目标一的TSM函数值始终大于目标四，是监控区域内威胁度最大的目标。直至t=13s时，目标二随时间推移，距离传感器中心位置越来越近，取代目标一，成为场景中最大威胁度目标，传感器调整自身位置开始朝向目标二运动。当t=31s时，目标二消亡，目标三威胁度变为最大，传感器适时调整自身轨迹向目标三方向运动。而目标四由于朝向远离传感器中心的位置运动，且在每个时刻都存在威胁度大于其的目标，因此，在监控时刻内未有时刻成为最大威胁度目标。通过图6，验证了“Proposed Threaten control”方案的有效性。这种控制方案基于战术重要性评估准则，考虑威胁度态势，始终确保传感器优先跟踪威胁度最大的目标。

图7为方案四“Proposed CS control”和方案五“Proposed Threaten control”针对最大威胁度目标跟踪的OSPA距离对比图，由图可知，方案五是针对最大威胁度目标的最优控制方案，其跟踪效果优于方案四，方案四则是针对系统整体的最优控制方案。这也验证了在不同优先级目标跟踪的复杂场景中，方案五具有更好的适用性，从而也说明了本章所提出的两种传感器控制方案在不同的多目标跟踪任务规划中都具有各自的优势，针对不同的应用场景中选取合适的控制方案才能达到最优的效果。

图7 基于最大威胁度目标的OSPA距离图

五种传感器控制方案对于目标势（数目）的估计如图8所示。由图可知，所有方案对于目标势估计的结果均都接近于真实目标数目，在目标新生或消亡的时刻，目标势会发生短暂的偏差，随后能迅速调整估计值。

图8 多目标势估计图

6 结语

本文的主要工作和创新点在于基于LMB滤波器，在信息驱动的传感器控制框架下，通过提升量测信息获取质量，最终实现滤波器跟踪性能的进一步提高。首先，通过求取目标先验、后验概率密度函数之间的CS散度，详细推导了评价函数解析解。然后，在多伯努利更新过程中采用“去标签”化处理，通过伪更新步骤，大幅降低了计算量，并提高了运行速度。其次，通过计算战术重要性评估指标——TSM函数，实现基于监控区域威胁度目标跟踪的传感器控制目的。最后，合理设立仿真场景，根据跟踪要求的侧重点不同，验证了所提算法的有效性及实用性。