Revisiting the period and quality factor of the Chandler wobble and its possible geomagnetic jerk excitation

Ychong An , Ho Ding ,b,*

a Department of Geophysics,School of Geodesy and Geomatics,Key Laboratory of Geospace Environment and Geodesy of the Ministry of Education,Wuhan University, 430079 Wuhan, China

b Hubei LuoJia Laboratory, 430079 Wuhan, China

Keywords:Chandler wobble Quality factor De-convolution Geomagnetic jerks

ABSTRACT The period and quality factor of the Chandler wobble(CW)are useful for constraining the Earth's internal structure properties, such as the mantle elasticity. It has been shown that the CW is mainly excited by a combination of atmospheric and oceanic processes; hence based on a deconvolution method, we can remove them from the excitation sequence of the CW to estimate its period P and quality factor Q. We finally re-estimate P = 432.3 ± 0.8 days and Q = 85 ± 15 for the CW. Based on those two estimates, we investigate the relationship between the geomagnetic jerks and the excitation sequences of the CW.The geomagnetic jerks or jerk bounds are well consistent with the sudden changes of the excitation sequences of the CW.This demonstrates that the geomagnetic jerks could be a possible excitation source of the CW. It is crucial for understanding the excitation of the CW and for deeper geophysical insights into the geomagnetic jerks.

1. Introduction

The orientation of the Earth in space changes due to the action of various external and internal torques.The internal dynamics that change the inertia tensor of the deformable Earth, or generate relative angular momentum,also cause the orientation of the Earth in space to change, the resulting motions being known as polar motion (PM) and the length-of-day variation [1]. The PM reflects the position change of the Earth's rotation axis relative to its body,measured for more than 50 years of high precision observation records.Chandler[2,3]summarized that this motion has two main periodic oscillations, the forced annual oscillation and an excited resonance of the eigenmode of the Earth's rotation,with a period of about 14 months being known as the Chandler wobble(CW)[4,5].Data analysis results have shown that both the amplitude and the phase of the CW are varying with time. Given that the CW is continuously excited, while its excitation mechanism has long remained elusive [6], it is difficult to accurately estimate the corresponding period P and quality factor Q of this wobble. Although many possible candidates (atmosphere [7-9], ocean [10,11], hydrology [12-14], and core-mantle interactions [15]) have been proposed for the excitations,a combined effect of atmospheric and oceanic processes seems rather convincing,as exposed in ref. [10].

Furthermore,based on wavelet analysis,Gibert et al.[16]found that phase jumps of the CW were correlated with the geomagnetic jerks, which is a sudden change in the second derivative of the Earth's magnetic field with respect to time. The origin of geomagnetic jerks from the Earth's exterior (e.g., solar cycle effect) or interior (i.e., the Earth's core) has been in dispute since the discovery of the 1969 event [17]. However, recent studies have indicated that it is more likely to come from the Earth's interior[18-24]. Bloxham et al. [25] demonstrated that geomagnetic jerks could be explained by the combination of a steady flow and a simple time-varying, axisymmetric, equatorially symmetric,toroidal zonal flow. This flow is consistent with torsional oscillations in the Earth's core, which is a kind of Alfv′en wave caused by azimuthal oscillation of rigid cylindrical surfaces aligned with the rotation axis and propagating perpendicular to rotating cylinders in the core [19]. In particular, Bellanger et al. [26] proposed that a jerk is the instability of a layer at the top of the core that moves downwards. This probably produces a pressure step at the core-mantle boundary,and hence a torque step,suggesting that the phase jump in the CW may be trigged by geomagnetic jerks[26-29].

In this study, we choose a de-convolution method to estimate the P and Q of the CW; such process was first used by Furuya and Chao [30]. Different from ref. [30], in which only the atmospheric effect is removed from the excitation sequence of the CW,here we remove both atmospheric and oceanic effects from the excitation sequence of the CW to re-estimate its P and Q. After obtaining the final estimates, we further use them to calculate the excitation sequence of CW. After removing the atmospheric and oceanic effects, we further search for a possible relationship between the geomagnetic jerks and the excitation of CW. If found, it indicates that the geomagnetic jerk is a new excitation source of the CW,which may give additional constraints on the geomagnetic jerk mechanism and new information on core dynamics [26].

2. Datasets and processing

The PM record (m = m1+im2; the m1-component along the Greenwich meridian and the m2-component along 90°E longitude)used in this work is obtained from the EOPC04 dataset as shown in Fig.1a (linear trends have been removed), the time span is 1962/01-2021/05 with 1-day sampling.Its Fourier spectrum(m1+im2)is shown in Fig.1b,and in this study,we focus on the CW band(about 0.8-0.9 cycle per year(cpy);blue area).From Fig.1b,the CW is the main oscillation, followed by the annual term and low-frequency oscillations, and some small oscillations of semi-annual and negative annual terms. The effective atmospheric angular momentum functions (AAMF) data (1948/01-2021/02 with 0.25day sampling)are downloaded from the Special Bureau for the Atmosphere, and we choose the inverted barometer (IB) pressure term as the used mass term. We decimate the AAMF (mass terms + motion terms)record from 0.25 days to 1-day sampling (after proper low-pass filtering, i.e., the cut-off frequency fcshould be less than 0.5 cpd to prevent aliasing; here, we use fc= 0.5 cpd). Besides, we also download the effective oceanic angular momentum functions(OAMF)data(mass terms+motion terms)from the Special Bureau for the Oceans.To compare with the PM record,we use two OAMF datasets here.The first one is OAM-ECCO_50yr,and its time span is 1949/01/06-2003/01/06 with 10-day sampling. The second is ECCO_kf080h and its time span is 1993/01/02-2020/03/30 with 1 day sampling. To combine them, we firstly choose a simple linear interpolation (the influence of interpolation can be ignored,because a given geomagnetic jerk occurrence time has 1-2 years uncertainty) on OAM-ECCO_50yr to obtain daily sampling, and then merge it with ECCO_kf080h to form a new sequence during 1949/01-2020/03 with 1 day sampling.

Finally, we select 1962/01-2020/03 as the common time span for the further analysis of PM, AAMF and OAMF time series.

3. The period and Q value of Chandler wobble

In this study, we adopt a de-convolution method [30,31] to estimate the period P and Q of the CW. This de-convolution method has been successfully used in previous studies[30,32]for the same purpose. In ref.[31], for the free core nutation, and in refs. [33,34]for the 6yr oscillation and the ～8yr oscillation, respectively. Here,we only provide a simple introduction for it, and recommend that readers refer to[30,31,33] for details.

The CW is a normal mode of the Earth rotation,and hence it can be written as the temporal convolution of harmonic oscillations with the excitation function χ(t) [35]:

where F denotes the Fourier transform operator,the m(t)and ω are known, thus, we can invert for the χ(t).

Suppose we do not know the true complex eigen frequency (P and Q value) of the normal mode in advance, a set of somewhat erroneous parameters (P, Q) are chosen as the input of deconvolution. When the (P, Q) has deviations with the true values,then the de-convolution notch filter would then be somewhat off the target and unable to remove the resonance power completely[31,34]. In addition to the true power, the obtained power of χ(t)also contains some extra power that should not exist. If the excitation is statistically independent of the observation noises, the resulting spectral power around the resonance frequency band will be artificially elevated.Conversely,the obtained χ(t)with the least power in the resonance frequency band will correspond to the correct (P, Q) [31,34].

For the CW,the external excitation sources are mainly from the atmosphere, ocean and hydrology. If the known excitations are removed from de-convolved time series to obtain χr1(t),the related power is greatly reduced. However, different hydrological models have clear deviations [33]. Here, we do not further consider hydrological effects.

In this de-convolution method, we set parameter P from 426 days to 440 days with 0.1-day interval,and set parameter Q from 10 to 160 with 3 as the interval. First, we calculate the excitation χ(t)with those different Qs and Ps, and then we obtain their residual time series χr1(t) by subtracting the AAMF and OAMF from the excitation χ(t). Finally, we calculate the resulting mean excitation power as a function of different input parameters(P,Q)in the band 0.8-0.9 cpy as shown in Fig. 2b. The relative minimum value is found at P≈432.3 days and Q≈85.We further calculate the Fourier power spectra of residual time series χr1(t)with 7 different Qs but the same P=432.3 days,shown in Fig.2b.We find that the power decreases as Q increases around the 0.845 cpy (432.3 days) until Q≈85, and then increases as Q increases. According to the above analyses, we determine P≈423.3 days and Q≈85 for the CW. For the more precise period,we obtain that P=432.3±0.8 days based on Monte Carlo statistics.Finally,we determine that P=432.3±0.8 days and Q=85±15 for the CW.Those values are different from ref.[36](in their study,P=430.9±0.7 days and Q=127 has the error range (56, 255)), which considers atmospheric, oceanic and hydrological effects based on this de-convolution method. This difference is mainly due to a shorter time series (only 1985-2010)used in their study.

4. Excitation of Chandler wobble and geomagnetic jerks

Fig.1. (a)The m1 and m2-component of the PM;the unit of the vertical coordinate is milliarcseconds(mas).(b)The Fourier spectrum of the complex PM(gray curve;m1+im2);blue area denotes the Chandler wobble band.

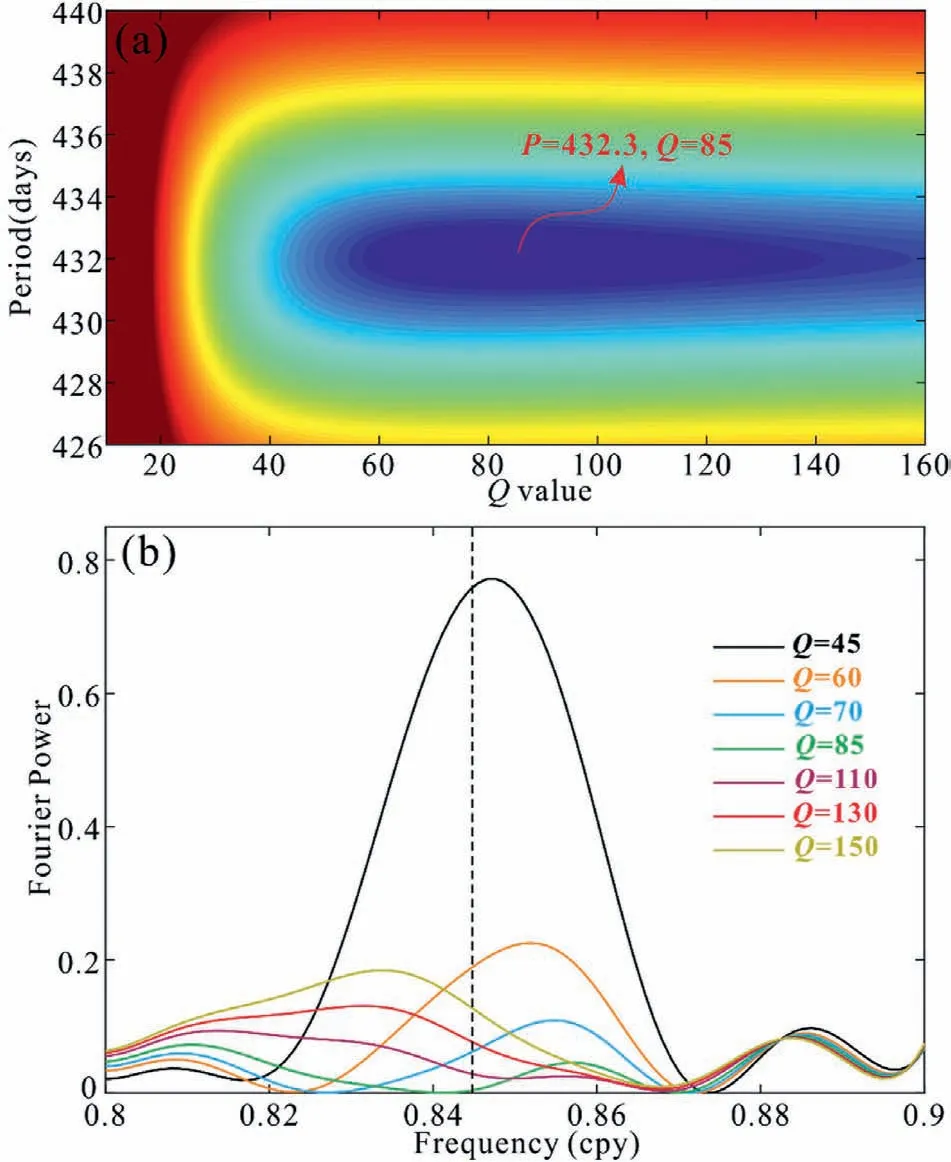
Fig. 2. (a) The relative mean power of the excitation χr1(t) for the CW as a function of the different input (P, Q). (b) The Fourier power spectra of the excitation χr1(t) (the AAMF and the OAMF have been removed) with different Qs, with P set as 0.845 cpy(432.3 days); black dashed line denotes the frequency of 0.845 cpy.

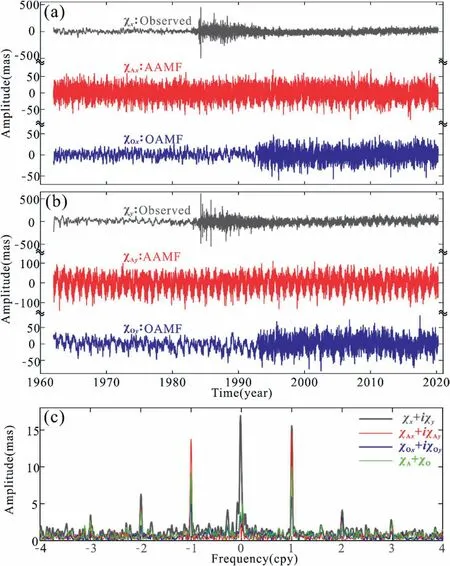
After determining the P and Q of the CW, we further calculate excitation sequences χ(t)(=χx+iχy)of the PM according to Eq.(1),the results are shown in Figs. 3a and 3b. We find that excitation amplitude became significantly larger after the 1980s. This is because small changes in the PM can be captured due to the improvement of observation technology.Strong seasonal terms can also be observed from the excitation sequences χ(t).The AAMF and OAMF are shown in Figs. 3a and 3b, respectively. Their Fourier spectra are shown in Fig. 3c. Fig. 3c demonstrates that the annual terms in the PM are mainly excited by the atmosphere.After adding oceanic effects, the spectrum is slightly reduced, which indicates that the atmosphere and ocean reduce each other in the (positive and negative)annual band. The negative annual term of the PM is almost explained by the sum of AAMF and OAMF. However, the amplitude of the positive annual term is smaller, implying that there should be other sources of excitation (perhaps hydrological effect). The amplitudes of atmosphere and ocean are almost the same in the positive semi-annual term, but atmosphere's amplitude is much larger than the ocean in negative semi-annual term.In addition,the atmosphere and ocean have only weak contributions to the excitation of the PM in low-frequency band,mainly because the AAM and OAM models have relatively low precision.

According to the above analysis, the high-frequency excitation of PM mainly comes from the atmosphere and ocean. After removing atmospheric and oceanic effects, we obtain the residual χr1(=χr1x+iχr1y)sequences.Its Fourier spectrum is shown in Fig.4a.It can be seen that there are still some seasonal signals remaining in the χr1sequences. After a high-pass filter (fc= 0.1 cpy), we fit and remove seasonal terms using the cosine periodic signals to obtain χr(t) (=χrx+iχry) sequences. The Fourier spectrum of the residual sequence after filtering of seasonal terms is shown in Fig.4a.The x and y components of the residual sequence are shown in Fig. 4b.The spectrum of χr(t) (purple curve) almost overlaps with the χr1(gray curve) in the target band, demonstrating that we obtain thepure excitation sequences of the CW after the above processing.However, Fig. 4b shows that it is quite difficult to directly infer useful information for the sudden changes; this is mainly because there is still some higher frequency noise present in the residual sequences,especially around 1980.To show some possible sudden changes more clearly,we used a median filter to reduce some noise effects. Here, we use a 1-D median filter with an n = 100 days window to the excitation sequences χr(t).The obtained time series χM(t) (=χMx+iχMy) does show some sudden changes, as in Fig. 4c.However, the correspondence relationship between χM(t) and geomagnetic jerks is still not very clear.

To more clearly show the sudden changes of the time series χM(t), we calculate its second-time derivative χd(t) (=χdx+iχdy), as shown in Fig.5a.Fig.5a shows the x-component and y-component of the χd(t) sequences, which show much more sudden changes than Fig. 4b. Besides, the precision of OAMF record has been improved since 1993 due to satellite altimetry.Thus,the χd(t)has a lower amplitude after 1993.When the χd(t)is displayed at the same scale, some useful information will be obscured after 1993.Hence,we further use the normal Morlet wavelet transform to detect sudden changes of the χd(t)to compare them with geomagnetic jerks. The normal Morlet wavelet transform of function f(t) is defined as [37,38].

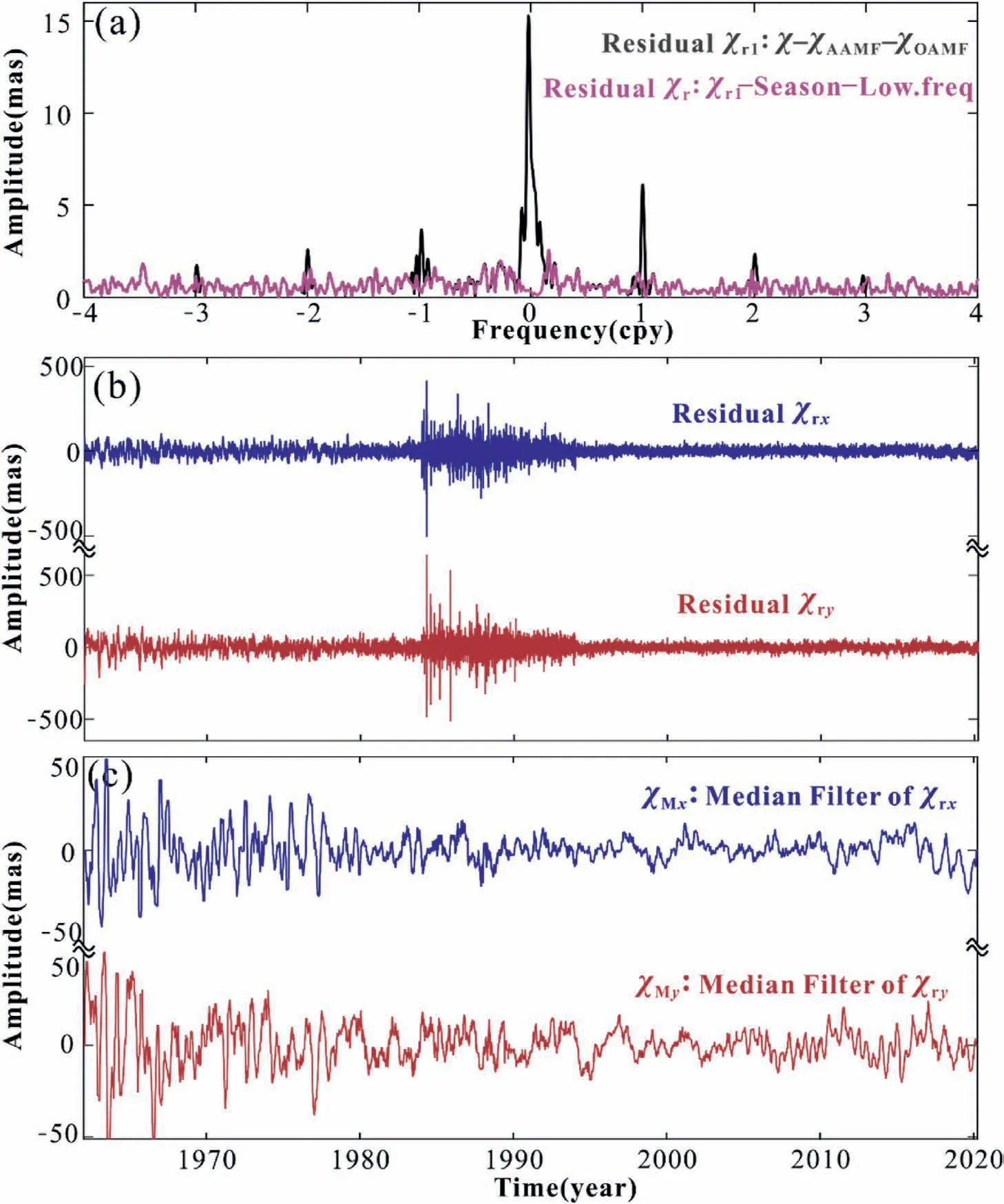
Fig.4. (a)The Fourier spectra of the residual χr1(t),in which the AAMF and OAMF effects have been removed,and the residual χr(t),in which the AAMF,OAMF effects,seasonal and low-frequency terms have been removed. (b) Two components of the residual excitation sequence of the CW where the AAMF and the OAMF were removed. (c) The 1-D median filter of the time series in (b).

where σ ＞0 denotes the window width parameter. To detect the same sudden change in the x-component and y-component of theχd(t) sequences, we draw a cross power spectrum of them in Fig. 5b. The normal Morlet wavelet cross power of functions X(t)and Y(t) is defined as

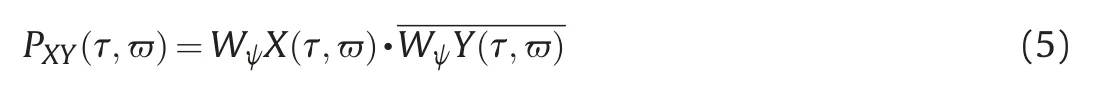
The spectral values in Fig. 5b are shown on the log2 scale, the same as Refs. [34,39]. To facilitate comparison, we marked the epochs of geomagnetic jerks and shaded jerk bounds.We also used white circles to mark the detected corresponding sudden changes of the χd(t) sequences.

During the study period, geomagnetic jerks occurred in 1963,1965,1969,1972,1978,1982,1986,1991,1995,1999,2003.5,2004.7,2007,2011,2014 and 2017[18,20,40-48].The best known,and the most studied,geomagnetic jerks around 1969 and 1978 are global,which have similar spatial structures but of opposite signs and 2-yr delay from the southern hemisphere to the northern hemisphere[39,47,48,51]. In addition, geomagnetic jerks around 1971, 1980,1991 and 1992 are also global events and have various regional delays [47,48,51-53]. The other jerks are local [18,42,51,54-56]except the 1999 event,which is debated over whether it is global or local [51,54,55]. More and more observations suggest that a given jerk does not occur simultaneously in different regions of the Earth's surface as it has 1-2 years uncertainty [20,40,57]. If we follow the inferences in ref. [39], the sudden changes in the amplitude of χd(t) can approximately be found around the time of geomagnetic jerks from the Fig. 5b. Considering the jerk bounds(gray areas),the geomagnetic jerks seem to be consistent with the sudden changes in χd(t).However,not all the sudden changes in the amplitude of χd(t) correspond to geomagnetic jerks.This indicates that the geomagnetic jerks may be one kind of excitation source of the CW.

5. Discussion and conclusion

Fig. 5. (a) The second derivative of the time series in Fig.4b. (b) the normal Morlet wavelet cross spectrum of the χd(t) time series in (a). Black dashed lines denote the epochs of geomagnetic jerks, the gray areas indicate the jerk bounds from [18,20,40-50], and white circles mark the detected corresponding sudden changes of the χd(t) sequences.

Taking into account the atmospheric and the oceanic effects,we estimate the P and Q of the CW upon using the de-convolution method. After deconvoluting the PM to obtain its excitation sequences, we subtract the AAMF and OAMF from the excitation sequences. Around P≈423.3 days and Q≈85, the mean excitation powers are clearly lower than the others,indicating that the Q of the CW should be about 85.Finally,we determine that a P=432.3±0.8 days and Q= 85±15 for the CW,which are different from ref.[36](P = 430.9 ± 0.7 days and Q = 127). The new value is closer to the theoretical value of 433.2 days and 85.4 predicted by a triaxial threelayered anelastic Earth rotation theory, considering various coremantle couplings, including the pressure and gravitational couplings acting on the elastic inner core by the outer core and mantle,and the visco-electromagnetic couplings between the outer core and mantle and between the outer and inner cores[58].

Based on the new estimates for P and Q of the CW, we further calculate the excitation sequences of the PM. Robust evidence shows that the excitation sources of the PM seasonal terms are mainly from the atmosphere (the largest external excitation sources)and ocean in a high-frequency band.After removing AAMF and OAMF, the residual sequences are processed by using a high-pass filter. Finally, we also fit and remove seasonal terms from the sequences to obtain the excitation of the CW.The obtained excitation sequences are probably mainly from the hydrology and the Earth's interior (perhaps core motions). Some useful information can hardly appear due to the high background noise in the excitation sequences,and hence we process the sequences using 1-D median filter.Although some sudden changes can be seen from the filtered sequences,we still further calculate its second derivative to clearly show small changes. The x-component and y-component of the χd(t)sequences show some differences.To explore the relationship between the χd(t)sequences and jerks,we drew the normal Morlet wavelet transform cross power spectrum of the x-component and y-component of the χd(t). We find that geomagnetic jerks or jerk bounds seem to be related to the sudden changes in the excitation of the CW.

This is the first time that geomagnetic jerks and the excitation sequence of the CW are directly compared.The sudden changes in χd(t) will cause the sudden changes in the instantaneous amplitude,period and phase of the CW,not just a phase jump.Our comparison helps to directly determine whether jerks are possible excitation sources of the CW. A possible excitation mechanism as mentioned in ref.[26]is its origin in the instability of a layer at the top of the core. This mechanism produces a step-like variation of the torque, further influencing the Chandler wobble and resulting magnetic field variation. Nevertheless, further observational evidence and physical mechanism analysis are still needed. Confirming the correlation between CW and jerks is very important for understanding the interaction between the mantle and outer core and to deeper geophysical insights about the geomagnetic jerks.

Author statement

Both authors reviewed the results and approved the final version of the manuscript.We confirm that this work is original and has not been published elsewhere nor is it currently under consideration for publication elsewhere.

Data availability statement

The PM data used in this study can be downloaded from IERS(www.iers.org/IERS/EN/DataProducts/EarthOrientationData/eop.html); The AAMF, and OAMF datasets were downloaded from:www.iers.org/IERS/EN/DataProducts/GeophysicalFluidsData/geoFluids.html.

Conflicts of interest

The authors declare that there is no conflict of interest.

Acknowledgments

The authors thank Hagay Amit for valuable suggestions and comments. This work is supported by the NSFC (grants No.41774024,41721003,41974022)and by Educational Commission of Hubei Province of China (grant No.2020CFA109) and the Project Supported by the Special Fund of Hubei Luojia Laboratory.